Orlando Durán y José Aguiló
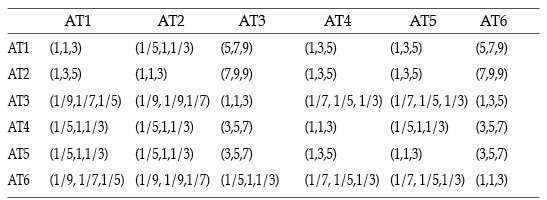
En esta sección, la metodología propuesta anteriormente es aplicada a través de un ejemplo numérico. Suponga que un grupo de analistas ha sido designado para evaluar tres alternativas de Máquinas Herramientas Automatizadas (Maq1, Maq2, Maq3). Este análisis será hecha considerando una serie de seis atributos cualitativos: Flexibilidad del Equipo, Facilidad de Operación, Confiabilidad, Calidad, Facilidad de Instalación y de Manutención. Estos seis atributos serán referidos de aquí en adelante como AT1, AT2, AT3, AT4, AT5 y AT6 respectivamente. Una vez que los analistas han realizado las comparaciones paritarias se obtiene la siguiente matriz del tipo A. En esta matriz las relaciones de comparación entre criterios ha sido hecha utilizando las escala de Saaty pero ahora con números triangulares.

Note que esta matriz representa cuan importante es para un conjunto de decisores un determinad atributo por sobre otro en particular.
A partir de esta matriz se debe calcular el autovector, el autovalro y el Indice RC. Ahora realizando las operaciones sobre los números triangulares y que fueron comentadas en el apartado anterior.
De esta forma se obtiene el siguiente autovector de números triangulares:
V = ((1,3 2,3 4,3) (1,9 3,6 5,6) (0, 3 0,4 0,6) (0,6 0,98 2,3) (0,8 1,4 3,0) (0,2 0,2 0,5))
Antes de proceder a realizar las normalizaciones es necesario considerar un alcance en relación con el ranqueo o comparación de valores difusos. El objetivo de este ranqueo es definir cuales valores son mayores y menores, estableciendo un ordenamiento lineal entre los valores. Existen diversas formas para realizar esta ordenamiento, entre los que se destacan el método del ordinal representativo, que esta dado por la siguiente relación:
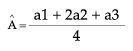
Donde A=(a1, a2, a3) es un número triangular. Â será entonces el ordinal representativo de cada número triangular. El segundo criterio para ordenación lineal consiste apenas en considerar el elemento central de la tripleta, o sea a2. El tercer método utilizado tradicionalmente para la ordenación lineal consiste en calcular la divergencia, o sea, la diferencia entre a3 y a1. Será considerado mayor el número que para elementos a2 iguales tenga mayor divergencia.
En nuestro ejemplo, se ha ocupado el primer criterio comentado anteriormente. Con esto se considera el segundo elemento del autovector como el mayor de ellos. Observe que según el segundo criterio del valor central también este elemento es considerado como el mayor de los elementos del autovector. Recordemos que el mencionado segundo elemento de este autovector corresponde al AT2 que representa a la facilidad de operación.
Después de las normalizaciones el autovector queda de la siguiente forma:
V = ((0,03 0,26 2,42) (0,04 0,40 3,17) (0,01 0,04 0,34) (0,01 0,11 1,30) (0,02 0,16 1,70) (0,004 0,03 0,26))
Para probar la consistencia de la respuesta, o sea, verificar que los datos están lógicamente relacionados, Saaty propone la siguiente relación
![]()
Donde el elemento w es calculado por la sumatoria de las columnas de la matriz de preferencias, o sea:
W = ((2,6 5,0 10,4) (1,8 2,2 6,3) (19,2 27,3 36,0) (4,3 10,4 18,7) (3,5 7,7 14,7) (20,0 30,0 40,0))
Podemos estimar el max obteniendo el siguiente número triangular
![]()
para la obtención del Indice de Consistencia (escalar), proponemos utilizar el valor central del número triangular max
IC = (6,47- 6)/ 5 = 0,09
Conjuntamente se procede al cálculo de RC en función del índice randómico retirado de la tabla sugerida por Saaty para el número de atributos igual a seis.
De esta manera tenemos
RC = 0,09/1.24 = 0,07 < 0,10 lo que indica la total consistencia de las evaluaciones o comparaciones expresadas en la matriz de comparaciones. De esta etapa se puede concluir que el vector de pesos o preferencias entre los atributos (autovector V) considerados en el análisis representa las importancias otorgadas por los especialistas a estos atributos en el siguiente orden: AT2,AT1, AT5, AT4, AT3 y AT6.
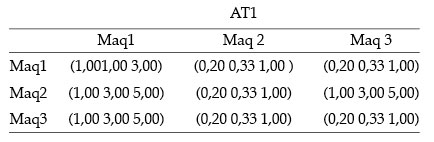
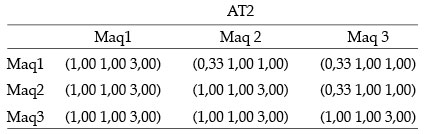
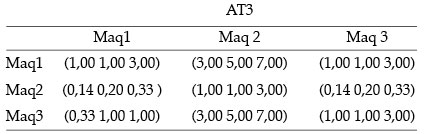
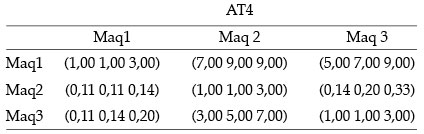
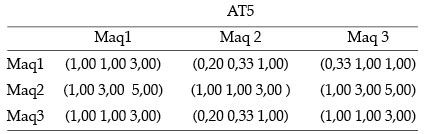
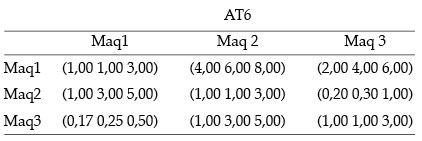
Autovector para comparaciones entre máquinas según los seis atributos considerados en el análisis:
VAT1 = ((0,1 0,2 1,0) (0,1 0,5 1,8) (0,1 0,3 1,4))
VAT2 = ((0,1 0,3 0,8) (0,1 0,3 1,0) (0,1 0,3 1,2))
VAT3 = ((0,2 0,4 1,2) (0,1 0,2 0,5) (0,1 0,4 1,0))
VAT4 = ((0,3 0,6 1,1) (0,10,2 0,3) (0,1 0,3 0,6))
VAT5 = ((0,1 0,3 1,0) (0,1 0,5 1,8) (0,1 0,3 1,2))
VAT6 = ((0,2 0,5 1,3) (0,1 0,3 0,9) (0,1 0,3 0,8))
Para la obtención del ranqueo de las máquinas se multiplica el autovector relativo a las máquinas según cada uno de los atributos por el autovector de la importancia de los atributos bajo análisis (todos los elementos de estos autovectores son números triangulares) obteniéndose el vector final, que muestra el ranqueo para cada una de las tres alternativas de máquinas bajo análisis, como se muestra abajo:
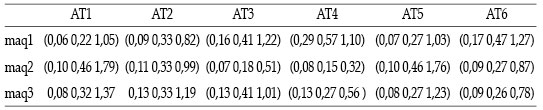
Realizada esta multiplicación se ha obtenido el siguiente vector
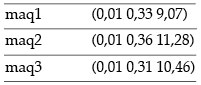
Abajo se muestra el criterio de ordenamiento lineal que muestra que la máquina 2 es la más apropiada para la selección según los atributos considerados y su importancia relativa.
Maq 1 2,43
Maq 2 3,00
Maq 3 2,77