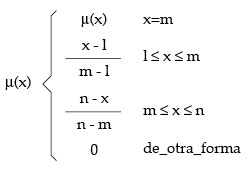
Orlando Durán y José Aguiló
La metodología propuesta considera incorporar los números difusos o triangulares a la metodología AHP. Inicialmente se utilizan los números difusos para indicar el nivel de intensidad o importancia relativa que un factor de la jerarquía tiene por sobre otro. A partir de estas comparaciones se construye la matriz de comparaciones con números triangulares. La mejor alternativa es obtenida consecuentemente a partir de un sistema de ranqueo para números difusos que se presenta más adelante en esta sección. Sintetizando, la aplicación de la metodología propuesta considera las tres etapas siguientes:
Recordando que el método AHP es un método que permite atribuir pesos donde valores numéricos no pueden ser obtenidos directamente. Este método trabaja a partir de una matriz donde se localizan las comparaciones entre pares, según la importancia o preponderancia relativa que un elemento de la jerarquía tenga sobre otro. Se propone aquí modificar la escala de Saaty utilizando ahora números triangulares o fuzzy.
Un número difuso del tipo triangular (Ã) es usualmente representado como una tripleta (l,m,n) donde m, n y l corresponden al valor medio, y a los límites superior e inferior respectivamente. Esta es la utilización que se empleará en el resto de este trabajo.
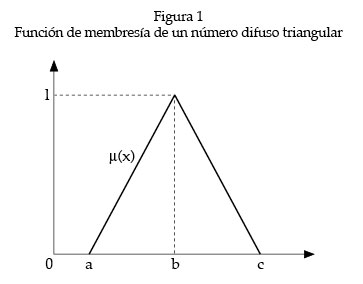
En general para los números triangulares difusos del tipo =(l,m,n), la función de membresía (x) está dada por la definición mostrada abajo y puede ser representada como en la figura 1.
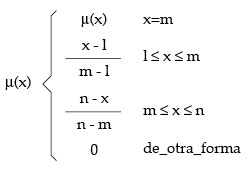
Explicamos a continuación la operatoria entre números triangulares (Chiu y Park, 1998). El producto entre dos o más números triangulares esta dado por
Por otro lado, la división entre dos números triangulares o difusos está expresado por:
Mientras que el valor recíproco de un número triangular (a, b, c) es (1/a, 1/b, 1/c). De la misma forma la potencia de un número triangular está dada por
(a1, a2, a3)n = (a1n, b2n, c3n)
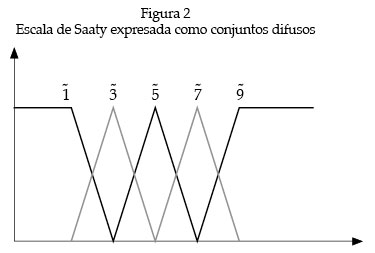
De la figura 2 se puede apreciar que la importancia relativa entre dos elementos es gradual y no abrupta
Por otro lado, sean
w1 = pesos expresados como números triangulares donde n = 1, 2, ...... , número de atributos
los elementos de la matriz de comparación aij serán una estimativa de la relación wi/wj. Tenemos entonces la matriz:
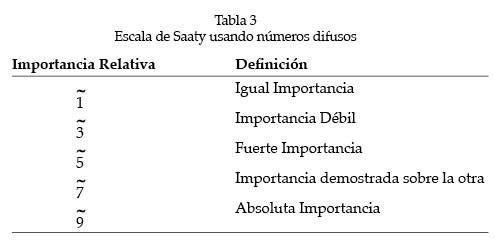
Los juicios u opiniones según la escala de Saaty se representan por números difusos triangulares 1, 3, 5, 7, 9 donde la definición de estos números está dada en la tabla 3 y sus funciones de membresía en la tabla 2.
Sabemos que la matriz A tiene todas sus entradas valores reales y positivos. También se debe cumplir que ãij = 1 / ãji. Por lo tanto A es una matriz recíproca positiva.
Seguidamente se procede a calcular el autovector, el autovalor y el índice RC, considerando ahora que los elementos a ij son números difusos o triangulares.
Para estimar el autovector V de la matriz A se utiliza la siguiente ecuación
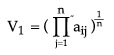
Tenemos así
hasta
De esta forma se puede obtener el autovector Vi formado por n números triangulares que tiene la forma:
V = (V1, V2, ...Vn)
Donde Vi es un número triangular de la forma (Vl, Vm, Vu)
De la misma forma que en el AHP tradicional el autovector debe ser normalizado y posteriormente pasar por otro proceso de normalización para que la sumatoria de sus elementos sea igual a 1; para realizar esto basta con calcular la proporción de cada elemento del autovector normalizado en relación a la sumatoria de los elementos del autovector.
Donde T es el autovector normalizado y es utilizado para cuantificar y ponderar la importancia de las características o atributos en análisis.
Un paso o etapa importante del método AHP es la prueba de consistencia de la respuesta dada por los especialistas, o sea si los datos están o no lógicamente relacionados. El método es semejante al utilizado cuando se utilizan los números crisp.
Se estima inicialmente el autovector 
, donde la estimativa está dada por
donde w es el número triangular que representa la sumatoria de las columnas de la matriz de comparaciones.
Posteriormente se calcula el Índice de Consistencia (IC) a través de la expresión:
Como, según la operatoria para obtener el , este también será representado por un número triangular, debemos transformarlo a un número crisp para viabilizar el cálculo del IC. De esta manera proponemos usar aquí el valor central de número triangular que representa (por su simetría) la posición del centroide del triángulo que corresponde al número triangular max.