ISSN 0798 1015

Vol. 41 (Issue 11) Year 2020. Page 2

Multicriteria method for the evaluation of learning in the subject Mathematical Foundations of the Information Technology degree

Método multicriterio para la evaluación del aprendizaje en la asignatura Fundamentos Matemáticos de la carrera Tecnologías de la Información

RODRÍGUEZ-RODRÍGUEZ, Alberto 1; PINO-TARRAGÓ, Julio.C. 2; LLANES-CEDEÑO, Edilberto A. 3; QUIMIS SÁNCHEZ, Omar A. 4; VIGOA-ESCOBEDO, Yisell. 5

Received: 16/08/2019 • Approved: 23/03/2020 • Published: 02/04/2020

Contents

1. Introduction

2. Methodology

3. Results and discussion

4. Conclusions

Referencias bibliográficas

1. Introduction

In the teaching-learning process, evaluation is the process by which the overall performance of the student is estimated and is essential for the student to strive to improve the quality of their learning. A good evaluation system can also identify learning problems, from which it is possible to make decisions about the need to retrain or take advantage of the potential created by influencing individual differences (Rodríguez, 2010; Salas, 2010).

Decision-making represents the process of selection among alternative courses, based on a set of criteria, to achieve one or more objectives (Franklin, 2011; Simon, 1960). It also includes the process of identifying a problem or opportunity and the selection of an alternative action among several existing, is a key activity in all types of organization.

The decision process consists of four fundamental stages. Diagnosis: is to detect what is the problem or set of problems that affect the process. Design: it allows to model the different alternatives by means of which, a priori, it is possible to solve the problem diagnosed. Choice: phase in which the best strategy or alternative of the set is selected. Review: an analysis is carried out on the degree to which the strategy selected and executed has managed to solve the problem.

Decision-making problems can be classified according to the decision environment as a decision-making problem in an environment of certainty, uncertainty environment and risk environment (Leyva, 2013). An outline of the decision-making process proposed by Clemen and Reilly (2013) is shown in Figure 1.

Figure 1
Decision-making process

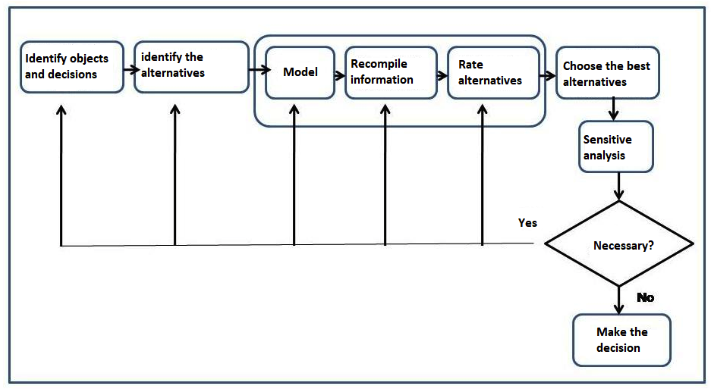
Source: Own elaboration

In a decision-making problem in a certain environment, the elements involved in the problem are precisely known, where it is possible to assign an exact value of utility to the alternative involved. However, for a decision-making problem in an environment of uncertainty, the necessary information is not available or is inaccurate; it is associated with subjective criteria of the problem being analyzed. The result of the inference is conditioned by the method and configuration used, considered as a complex decision problem.

For a decision-making problem in a risk environment, one or more elements of the process are subject to chance. For this classification, the resolution of the decision-making problem is based on the theory of probability where the probabilities are assigned to the alternatives (Bouza, 2016; Grajales-Quintero et al.,   2013).

When a decision-making problem meets (equation 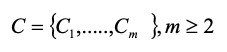1):

    (1)

Where:
C: the number of criteria
m: number of criteria

It corresponds to a problem of multicriteria decision-making. In the decision process there is a set of criteria that are valued to infer certain behavior on the alternatives (Garza-Rios et al., 2012; Leyva, 2013).

For the Mathematics Fundamentals course of the Information Technology degree at the State University of the South of Manabí (UNESUM) of Ecuador, an evaluation system has the following characteristics:

Frequent evaluations that are applied in various activities in classes, initial written question as diagnostic evaluation and formative evaluation such as the verification at the beginning of each conference, practical classes, guides for the observation of these practices based on the theoretical contents studied, integrative seminars to link the content with their specialty and with life, contributions.

Final evaluation or summative evaluation: partial exams at the end of each period.

From the existing evaluation system, an evaluation process is identified that can be modeled as a problem of multicriteria decision making where, from a set of indicators to be measured, it is possible to evaluate the alternatives.

Formally, it is represented as:

The evaluation criteria may belong to any of the evaluation forms. Therefore, the problem of decision-making can be modeled for a specific case of the evaluation of learning as a practical class or a more general application as a final evaluation.

Based on the aforementioned analysis, the objective of the present investigation is defined: to evaluate the learning of the Mathematical Foundations subject of the Information Technology degree at the UNESUM of Ecuador, through the application of the multicriteria method for decision making in the teaching learning process.

Soft computing techniques are used, conceived as a branch of Artificial Intelligence that encompasses various techniques used to solve problems that handle incomplete, uncertain and / or inaccurate information.

The methodology used to develop the research is based on a quantitative approach, where the observation and evaluation of the object is carried out. The degree of foundation of the proposal is demonstrated from the use of the scientific method as addressed by Hernández et., (2010). Next, a description of the main elements is made:

• The objective of the study is based on the use of multicriteria methods for the evaluation of learning.
• The research is delimited from the implementation of Soft Computing techniques to represent the uncertainty about the evaluation of learning.
• The result of the evaluations obtained by the students was used as a source of information.
• the research uses the literature review as a basis for the theoretical support used to conceptualize the proposed solution.
• The case study is used as an information collection technique to demonstrate the applicability of the proposed method.

The proposed method is designed to ensure workflow management in the decision-making process on learning assessment. It uses a multi-expert multicriteria approach where evaluative indicators are identified to nourish the functioning of the inference made by the method.

The evaluation process infers the behavior of the reasoning from the processing of the evaluation indicators (Singh, 2011; Cornelio, and González, 2018). The method consists of four activities as shown in Figure 2:

Figure 2
Activities that make up
the evaluation process

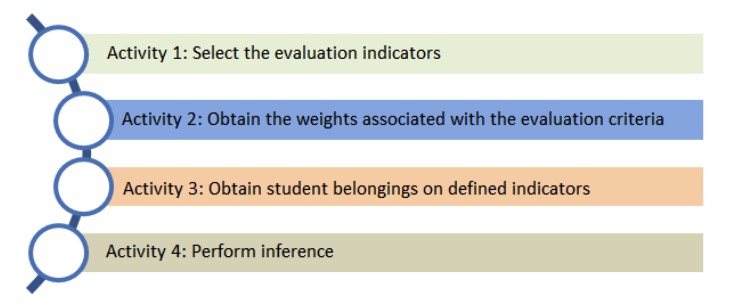
Source: Own elaboration.

Next, a description of the proposed activities is made.

Activity 1: the activity consists in identifying the evaluation indicators to be used (I), which represents the basis of the evaluation instrument that is applied to the students to obtain preferences on the indicators. The activity must comply to represent a multicriteria approach that the domain of values (n) obtained is finite, according to equation 2).

              (2)

Activity 2: Based on the use of a multi-expert approach, the activity of the group of evaluators becomes important and, through their daily interaction with the evaluation criteria, will allow refining the weight assigned to the indicators.

The weight is the value attributed to an indicator; weights will be determined through the assessments of the process experts. The experts are made up of a group of specialized professors with experience in the subject. These may express their preferences over the indicators through a linguistic label that corresponds to a numerical value. Table 1 shows the domain of values to use.

Table 1 
Domain of values to assign
weight to the indicators

Source: Own elaboration

From the preference obtained from each expert (E), the weight vectors (W) are obtained. The aggregation of knowledge allows improving the reliability of the final model, making it less susceptible to errors (Stach et al., 2010). As a result, a process of aggregation and standardization of the indicators is carried out according to equation 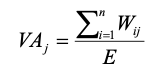3: 

           (3)

Where:
VA: normalized added value attributed to an indicator
E: the number of experts participating in the process
Wij: vector of importance expressed by experts for indicators Ci.

The domain of values (0,1; 1) express the importance of the indicator, the greater the value of the importance, the greater the weight attributed to the indicator. 

Activity 3: In order to obtain preferences, an evaluation form prepared previously with a group of proposed questions with their respective results is used, which in turn contribute to the fulfillment of the evaluation indicators. They are evaluated using a numerical scale so that the level of compliance of the indicators is expressed. 

Once the evaluation of the indicators assigned in the evaluation form is concluded, the preferences (P) are obtained for which the scale proposed in Table 2 is used.

Table 2
Domain of values to evaluate indicators

Source: Own elaboration.

Activity 4: The activity represents the core of the method processing. It is done by aggregating information through the information aggregation operator OWA (Ordered Weighted Averaging), Ordered Weighted Media (Yager, 1988). The proposed operator unifies the classic criteria of uncertainty decision in an expression (Filev and Yager, 1998; Cornelio et al.,   2017).

The aggregation is based on the idea of converting the multiobjective problem into a scalar one so that an objective function is constructed that is the sum of the objective starting functions, weighted according to a relative weight assigned to each of them. Thus, for each possible weighting, a scalar problem is obtained consisting of minimizing the resulting function, subject to the restrictions of the original problem (Rodríguez, 2015). The process of aggregation of information uses an important function described in equation 4, the competency vector is calculated.

From the result processed by the importance function, a vector is obtained that represents the learning of a student. Figure 3 shows the mastery of values that are used by the method in making decisions for the evaluation of student learning.

Figure 3
Domain of values for
decision-making on evaluation

Source: own elaboration

2.1. Sample Selection

To determine the sample size (n) of a finite population, equation 5 according to Sampieri (2018) is used. For the present study there is a population of 500 students from the State University of the South of Manabí (UNESUM) of Ecuador.

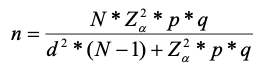   (5)

Where:

N = Total population

Zα= 1.96 (for 95% security)

p = expected proportion (in this case 5% = 0.05)

q = 1 - p (in this case 1 - 0.05 = 0.95)

d = accuracy (5% is assumed for the study).

The case analysis allows to demonstrate hypotheses raised by researchers in the course of an investigation. For the context of the present investigation, a case study was implemented with the objective of applying the proposal to a real environment and assessing the results.

The proposal was applied to a group of students of the Information Technology of the UNESUM of Ecuador for the Mathematical Foundations course. It was taken as an object of learning in the diagnostic evaluation that is carried out at the beginning of a certain subject. This type of evaluation was chosen because it allows us to understand what state the students are at the beginning of the topic and from the results make decisions that facilitate and improve learning during the development of the educational process.

Below are the assessments achieved by each stage:

Activity 1

For the activity, we start from the normative documents of the subject under study and identify the indicators that represent the main objectives to be evaluated by a subject or the subject in general. Indicators are the key element for further processing. Table 3 displays the evaluation indicators obtained from the activity.

Table 3
Evaluation indicators obtained

Sources: Own elaboration

Activity 2

To determine the weights on the criteria a multiexpero approach is used, in which between 7 and 13 experts must participate (Artola, 2002; Salina, 2004; Garza et al., 2012). For this investigation, 7 experts were employed. From the scale proposed in Table 1 and the standardization applied by equation 3, weights of the 7 evaluation indicators were obtained. Table 4 shows the result of the weight vectors resulting from the activity.

Table 4
Weights of indicators based on expert criteria

Sources: Own elaboration

Activity 3

In the experimentation, 64 students participated as a result of the calculated sample, which are randomly selected to demonstrate the applicability of the method.

Activity 4

From obtaining the importance function attributed to each student through the aggregation operator described in equation 4, a system of fuzzy values that are located in the domain of values for decision-making on the evaluation of learning proposed in Figure 3. In Figure 5, using a Pareto chart it can be concluded that 80% of the grades are between good and excellent.

Figure 4
Evaluation behavior applying
multi criteria method

Source: Own elaboration

From the data presented in Figure 5, outstanding students in their learning could be identified, which expresses an opportunity for use. By classifying students, the teacher can exploit this potential by guiding challenging activities. However, in the case of students who did not achieve satisfactory results, the project work strategy proposed by Llanes-Cedeño et al., 2018) can be applied, to thereby take advantage of the potential of 80 % satisfactory obtained in the evaluation of learning.

The inclusion of some activities, such as the evaluation indicator (I4) in the study program, has allowed us to increase the understanding of the minimum contents coinciding with the results obtained by Guardia et al., 2018) and Llanes et al., 2019).

From the implementation of the proposed method, it was possible to add weight vectors for the evaluation of the evaluation criteria that represented the basis of the decision-making process on the evaluation of student learning.

With the application of a case study it was possible to demonstrate the applicability of the method in a real context for the evaluation of learning, it was also identified from the learning behavior, the need to use the unexploited potential that obtained outstanding results and the need of training for students who did not achieve satisfactory results.

The application of the proposal was made in the Mathematical Fundamentals of UNESUM, although it can be extended to other subjects as it represents a work tool that will allow teachers to measure student learning.

Aquino, S. (2019). Práctica educativa para estudiantes de dinámica de máquinas utilizando la función de calidad. Revista ESPACIOS, 40(26). Recuperado de: http://www.revistaespacios.com/a19v40n26/19402622.html

Artola, M. (2002). Modelo de evaluación del desempeño de empresas perfeccionadas en el tránsito hacia empresas de clase en el sector de servicios ingenieros en Cuba. Universidad de Matanzas, 45-56.

Bouza, C. (2016). Métodos cuantitativos para la toma de decisiones en contabilidad, administración, economía. Disponible en: https://www.researchgate.net/publication/303551295_METODOS_CUANTITATIVOS_PARA_LA_TOMA_DE_DECISIONES_EN_CONTABILIDAD_ADMINISTRACION_ECONOMIA

Clemen, R. T., & Reilly, T. (2013). Making hard decisions with DecisionTools. Cengage Learning.

Cornelio, O. M., & González, J. G. (2018). Modelo para la evaluación de habilidades profesionales en un sistema de laboratorios a distancia. Revista científica, 3(33), 332-343.

Cornelio, O. M., Ching, I. S., Gulín, J. G., & Rozhnova, L. (2017). Competency assessment model for a virtual laboratory system and distance using fuzzy cognitive map. Investigación Operacional, 38(2), 170-179.

Filev, D., & Yager, R. R. (1998). On the issue of obtaining OWA operator weights. Fuzzy sets and systems, 94(2), 157-169.

Franklin Fincowsky, E. B. (2011). Toma de decisiones empresariales. Contabilidad y Negocios, 6(11).

Garza-Ríos, R., González-Sánchez, C., Pérez-Vergara, I., Martínez-Delgado, E., & Sanler-Cruz, M. (2012). Concepción de un procedimiento utilizando herramientas cuantitativas para mejorar el desempeño empresarial. Ingeniería Industrial, 33(3), 239-248.

Grajales-Quintero, A., Serrano-Moya  (2013). Los métodos y procesos multicriterio para la evaluación. Luna Azul, (36), 285-306.

Guardia, Y., Marquez, J., Sanchez, V., Llanes, E. A., Rocha, J. C., & Peralta, D. B. (2018). Mejoras a la asignatura Diseño Estadístico de Experimentos para estudiantes de la carrera de Ingeniería Mecánica. Revista ESPACIOS, 39(30). Recuperado de: https://www.revistaespacios.com/a18v39n30/18393010.html

Hernández Sampieri, R., Fernández Collado, C., y  Baptista Lucio, P. (2010). Metodología de la investigación: México: McGraw-Hill.

Leyva, M. (2013). Modelo de ayuda a la toma de decisiones basado en Mapas Cognitivos Difusos. (Tesis de Doctorado), Universidad de las Ciencias Informáticas. Disponible en: https://www.researchgate.net/publication/263221297_MODELO_DE_AYUDA_A_LA_TOMA_DE_DECISIONES_BASADO_EN_MAPAS_COGNITIVOS_DIFUSOS 

Llanes, E. A., Caiza, L., Andrade, J., Cardenas, A., Chamba, E., & Rocha, J. C. (2019). La formación basada en competencias en una dimensión gnoseológica de la carrera de automotriz. Revista ESPACIOS, 40(19). Recuperado de: https://www.revistaespacios.com/a19v40n19/19401909.html

Llanes-Cedeño, E. A., Rocha-Hoyos, J. C., Peralta, D. B., Martinez, J., & Celi, S. (2018). Project-based learning case of study education in automotive mechanical engineering. ESPACIOS, 39(25), 10. Recuperado de: https://www.revistaespacios.com/a18v39n25/18392510.html

Rodríguez, A. (2015). Modelo del proceso enseñanza-aprendizaje contextualizado de la asignatura Matemática. Tesis en opción al grado científico de Doctor en Ciencias. "Institut de Creativitat i Innovacions Educatives de la Universitat de València.

Rodríguez, J. F. O. (2010). Evaluación del desempeño del docente de la unidad educativa prof. fernando ramírez. Revista ICONO14 Revista científica de Comunicación y Tecnologías emergentes, 8(2), 58-70.

Salas Perea, R. S. (2010). Propuesta de estrategia para la evaluación del desempeño laboral de los médicos en Cuba. Educación Médica Superior, 24(3), 387-417.

Salinas, E. (2004). Procedimiento multicriterio-multiexperto para la toma de decisiones empresariales (Doctoral dissertation, tesis de diploma], La Habana, Instituto Superior Politécnico José Antonio Echeverría, Cujae, Facultad de Ingeniería Industrial, Departamento de Ingeniería Industrial).

Sampieri, R. H. (2018). Metodología de la investigación: las rutas cuantitativa, cualitativa y mixta. McGraw Hill Mexico.

Simon, H. A. (1960). The new science of management decision. New York.

Singh, A. (2011). Architecture value mapping: using fuzzy cognitive maps as a reasoning mechanism for multi-criteria conceptual design evaluation. (Tesis de Doctorado), Missouri University of Science and Technology.  

Stach, W., Kurgan, L., & Pedrycz, W. (2010). Expert-based and computational methods for developing fuzzy cognitive maps. In Fuzzy Cognitive Maps (pp. 23-41). Springer, Berlin, Heidelberg.

Yager, R. R. (1988). On ordered weighted averaging aggregation operators in multicriteria decisionmaking. IEEE Transactions on systems, Man, and Cybernetics, 18(1), 183-190.

1. PhD. Doctor of Science, Master degree of Education Sciences, Bachelor of Mathematics. Professor de la  Universidad Estatal del Sur de Manabí. Ecuador. alberto.rodriguez@unesum.edu.ec  

2. PhD Technical Sciences, Engineer. Teaching-Researcher. Professor de la Universidad Estatal del Sur de Manabí. julio.pino@unesum.edu.ec

3. PhD Technical Sciences, Teaching-Researcher, Faculty of Architecture and Engineering, Universidad Internacional SEK - Quito. Automotive Mechanical Engineer.antonio.llanes@uisek.edu.ec

4. Engineer,, Master in Accounting and Audit. Systems analyst. Facultad de Ciencias Técnicas de la Universidad Estatal del Sur de Manabí.omar.quimis@unesum.edu.ec

5. PhD. Doctor of Science, Master degree of Education Sciences, Bachelor of Special Education. Professor de la  Universidad de Ganma. Cuba. yvogoae@udg.co.cu