ISSN 0798 1015

Vol. 41 (Issue 09) Year 2020. Page 26

Methodology for the formation of a special course on applications of Markov processes

Metodología para la formación de un curso especial sobre aplicaciones de procesos de Markov

SUKHORUKOVA I.V. 1 & CHISTYAKOVA N.A. 2

Received: 03/12/2019 • Approved: 04/03/2020 • Published: 19/03/2020

Contents

1. Introduction

2. Methodology

3. Results

4. Conclusions

Bibliographic references

1. Introduction

In the new educational standard adopted in Russia, increased attention is paid to teaching students the skills of analyzing applied task settings. The standard requires the formation of graduates' professional competencies aimed at the competent use of acquired knowledge in solving emerging practical problems. This necessitated the intensive use of mathematical models in economic research and their more detailed study. One of the applied models for the study of problem statements in economic and technical fields is the Markov process model. However, the study of the Markov process at an economic university is usually either absent altogether, or it takes place very superficially in the course of probability theory. Therefore, it is advisable in advanced courses to return to a deeper education of students in the methods of analysis of Markov processes. It is necessary to introduce students to various statements of practical problems using models of Markov processes. The filling of the discipline substantially depends on the mathematical preparation of the students and the time allocated for its study. The number of topics and study materials can vary greatly for students with different levels of training. We offer the concept of the formation of a special course on applications of Markov processes based on the experience of teaching the discipline "Economic applications of Markov processes" for students in the areas of "Applied Mathematics and Computer Science", "Mathematical Methods in Economics" and "Management" in the Russian University of Economics G.V. Plekhanova. In contrast to the advanced course of Markov processes read for natural sciences at universities, the proofs of working theorems are significantly reduced here and ready-made algorithms for solving practical problems based on these theorems are proposed. This approach allows you to expand the professional and general cultural competencies of students, aimed at the application of mathematical methods of analysis in economic applications, and also forms a scientific worldview and helps to establish causal relationships in applied research. The practice of teaching a discipline in REU in the form of an elective discipline has shown its relevance by students and has consistently demonstrated interest in the tasks of this direction. Computer support for training significantly supplements students' independent work methods, diversifies it, develops modern data skills, saves time and makes  interested in quickly getting results.

1.1. Literature survey

Long before the start of the study of experiments with Markov dependence, concrete problems that belonged to this direction were already being solved ( Serfozo R.F. , 2005),  (Sukhorukova I.V., Methodical Aspects of Actuarial Mathematics Teaching , 2018) (Casas J.M., 2019). For example, the problem of bankruptcy of a player and the loss of capital by players after n games (Bernoulli,  Muavr) or the problem of the contents of an urn with balls when randomly selecting any ball and after n shifting the balls from the urn to the urn (Laplace).  (Sokolov G. A ., 2005),  (Kemeni D. D., 1970). However, the solution of these problems was carried out not within the framework of the general developed approach, but using methods for solving one specific problem.  (Sukhorukova I.V, 2018), (Popov V.A., 2018),  (Sukhorukova I.V, Insurance of the termination risk of projects with joint companion activity, 2019). The basic concepts of the theory of Markov chains were introduced and systematically studied by the famous Russian mathematician A.A. Markov in 1907. He paved the way for the formation of a general theory of Markov random processes.  (Demin S. S., 2018),  ( Sukhorukova I.V., Optimization of the Formation of the Capital Structure of the Insurance Company, Taking into Account the National Specifics of Insurance , 2018), (L. Kleinrock. , 1979),  (Howard R.A., 1977).His ideas in mathematical and philosophical plans were deeply developed in the work of our compatriot, the outstanding mathematician A.N. Kolmogorov  ( Kolmogorov A. , 1931). In 1931, in the article "On analytical methods in probability theory" Kolmogorov laid the foundations of the theory of random processes without aftereffect (when the past development of the process does not affect its future behavior and is determined only by the current state of the process. For the first time, direct and inverse differential equations were obtained to determine the transition probabilities, which are now called Kolmogorov equations. However, further development of this direction occurred avalanche-like. This is due to the fact that the theory of random processes and, in particular, the theory of Markov processes is a deep mathematical model for practical problems of various levels of complexity from a wide range of areas (Antoniou I., 2000), (Frank T.D., 2003),  (Muhly P.S., 2002),  (Gao F., 2003) .  It allows them to be systematically solved using the accumulated mathematical results.

In this article we want to dwell on the methodology of teaching the discipline "Economic application of Markov processes" at the Russian University of Economics. G.V. Plekhanov. Using the accumulated knowledge, we offer the concept of an educational and methodical program in this discipline. The purposes of the discipline are: the study of mathematical methods for analyzing discrete and continuous Markov chains, as well as the study of management methods for economic Markov processes. The objectives of the discipline are:

1. the construction of formal models of socio-economic processes in terms of discrete and continuous Markov chains;

2. analysis of the structure of the modeling process;

3. calculation of process characteristics;

4. the search for optimal management of the Markov process with revenues, maximizing the full expected income, marginal revenue or profit. (Sukhorukova I.V.,  Fomin. G., 2019)

For the successful development of the discipline, a previous study of the following disciplines is required: “Linear Algebra”, “Mathematical Analysis”, “Differential Equations”, “Probability Theory and Mathematical Statistics”. The student must know the basic definitions and properties of algebraic objects, methods of mathematical analysis and probability theory, master the technique of working with vector and matrix data on a computer, the technique of solving differential equations, calculating event probabilities and analyzing the behavior of random variables and random vectors.

The thematic plan for studying the discipline is designed for 56 hours of classroom work, 52 hours of independent work and includes the following topics: topic 1 - discrete Markov chains, topic 2 - managing discrete Markov chains with revenues, topic 3 - continuous Markov chains and related applied problems. The content of the discipline "Economic applications of Markov processes" is given below.

Topic 1. Discrete Markov chains

Main definitions. Kolmogorov-Chapman equations. Matrix of transition probabilities in n steps. The vector of system state probabilities in n steps. Analysis of the structure of the Markov chain: essential and non-essential states, decomposability and indecomposability of the chain, structure of the equivalence class (regular and cyclic), construction of cyclic subclasses of the equivalence class, canonical numbering of states and construction of the transition probability matrix in canonical form. Classification of discrete Markov chains. Stationary and motionless state probability vectors. Ergodic theorems of long-term prediction of the behavior of an irreducible, monoergodic, polyergodic absorbing chain and general polyergodic chain. An example of the task of ruining a player in a two-person game (calculating the probability of ruining each of the players with fixed initial bets and the probabilities of winning one bet, calculating the average duration of the game and the average winning of the player). An example of a Moran model in stock theory.

Topic 2. Management of discrete Markov chains with income

The concept of a discrete Markov chain with income. One-step revenue matrix. The vectors of the average one-step income and the total expected income of the system in n steps. The matrix equation for the total expected income of the system in n steps with and without interest rate and its computer solution. Asymptotics of the total expected income of the system. Concepts of strategy, policy and management for the Markov chain. The construction of optimal control that maximizes the total expected revenue of the system with a finite control horizon by the Bellman dynamic programming method. Howard constructs an optimal control that maximizes marginal revenue or profit in the class of stationary controls with an infinite control horizon.

Topic 3. Continuous Markov chains and related applied problems.

The simplest stream of events and the Poisson process, its properties. Kolmogorov differential-difference equations for the probabilities of states of a continuous circuit at an arbitrary instant of time and their solution using the Laplace transform, stationary probabilities of states. Processes of death and reproduction with continuous time, their special cases. Differential equations for state probabilities at an arbitrary point in time and their solution, stationary mode. Applied problems of the analysis of processes and service systems, using continuous Markov chains.

To conduct classes you need a computer audience with a blackboard. At the same time, obtaining the characteristics of the circuit through algebraic transformations is significantly accelerated. Undergraduate students usually quickly deal with such computer calculations in a Microsoft Excel spreadsheet processor.

On topic 1, it is proposed to solve problems of both theoretical and computational nature, from the problem books and textbooks listed in the list of references. We give examples of problems on this topic.

Task 1. There are three computers in the data center. Everyone during the day can break down with a probability of q = 0.3 and get up for repairs. The probability of repair during the day is r = 0.2. In one day, the computer cannot break and repair. The state of the system at time n- is the number of operational computers at that moment. Describe the functioning of the system in the form of a Markov chain; give a complete structural analysis of the chain. Find the matrix of transition probabilities and the vector of probabilities of the states of the circuit after a week of operation, if at the initial moment all the computers are operational.

Task 2. In the process of monthly repayment of the loan issued, a bank client may be in one of the following conditions

   - the monthly payment is paid off on time in full,

   - the monthly payment is paid off in full, but with a time delay,

  - the monthly payment is paid off on time in an incomplete amount with the transfer of the balance of the debt to the next month,

   - the monthly payment is repaid with a temporary delay and in part with the transfer of the balance of the debt to the next month.

 Successive states form a Markov chain with a transition probability matrix of the form

Give a complete structural analysis of the circuit. Find the probabilities of conditions after three months if the first payment was due.

Problem 3. Suppose that in a certain city, 4% of the inhabitants move to the suburbs every year, and 1% of the suburban residents move to the city. Assuming that the total number of inhabitants remains constant, describe the process of population redistribution in the form of a Markov chain, give a complete structural analysis of the chain. Find the transition probability matrix, find the final distribution of residents between the city and the suburbs.

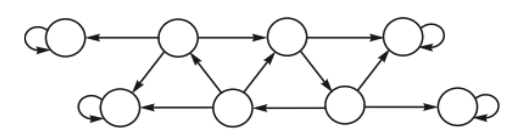
On topic 1, the work program of the discipline provides for individual calculation and analytical work, consisting of an analysis of three discrete Markov chains of increasing complexity: the first is an irreducible or monoergodic chain, the second is a polyergodic absorbing chain, and the third is a general polyergodic chain. We give one version of the graphs of Markov chains for computational and analytical work.

Figure  graph  1
Irreducible, or monoergodic chain
(made by authors)

Figure graph 2
Polyergodic absorption chain
(made by authors)

-----

Figure graph 3
General polyester chain
(made by authors)

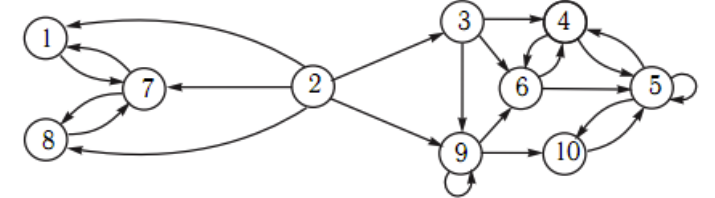
Having received his individual graphs of Markov chains, the student first performs a written homework on the structural analysis of chains and submits it for verification. These include the following tasks:

1. give a complete structural analysis of the Markov chain, introducing the canonical numbering of states, determine the type of chain;

2. set transition probabilities by marking them on the state graph;

 3. find the transition matrix in canonical form.

After checking the assignments and correcting errors, the second part of the calculated assignment is performed in a class in a computer class. These include the following tasks:

1. set the equiprobable vector of initial probabilities of the states of the circuit and find the vector of probabilities of states of the chain in three steps;

 2. Using the corresponding ergodic theorem, find the final matrix of chain transition              probabilities and the stationary state vector of probabilities. Give a semantic interpretation of different fragments of the final transition probability matrix.

Topic 2 discusses the theory and tasks of obtaining the full expected income and the search for optimal management of the Markov chain with incomes. Here are some examples.

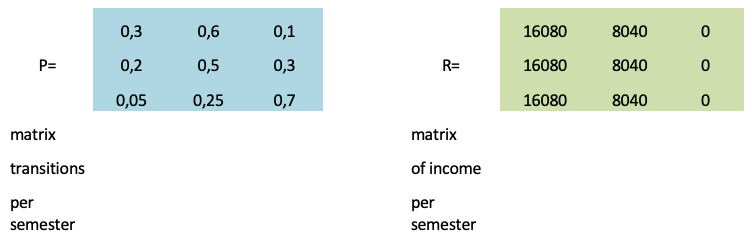
Task 4. When passing the session, an excellent scholarship is perfectly assigned, when passing the sessions on 4 and 5 - the usual scholarship. Student's condition = 1, 2, 3 if he has an increased scholarship, regular scholarship, or no scholarship, respectively. Matrices of transition probabilities and one-step revenues are P and R and are given below. Find the full expected income for 4 years of study of a randomly selected student if the discount factor for the semester is 0.95. What is the total expected income equal if the student began to study without a scholarship? What is the average amount of the scholarship fund spent on all students if in the first semester everyone is paid a regular scholarship, and in a university there are 2,000 students?

Table 1
Transition probabilities and one-step
revenue matrices per semester

Task 5. Annually, you can choose a state or private management company to store your pension savings (state 1 and 2, respectively). System Status — the selected company type. Matrices of transition probabilities and one-step incomes are of the form P and R and are given below. Find the marginal total expected income if the interest rate is 7%.

Table 2
Transition probabilities and one-step
revenue matrices for the year

Task 7. Continuing the consideration of the task of the head of the company, find the marginal income if the interest rate is 6%.

Task 9. We continue to consider the tasks of the head of the company. Using Bellman’s dynamic programming method, find the optimal management and the corresponding value of the total expected income if the management horizon is 5 months and the interest rate is not taken into account.

We turn to topic 3, in which, as indicated above, Markov chains with continuous time and related applied problems are investigated. We give examples of problems on this topic.

Task 10. Buyers form the simplest intensity flow 3. The probability that the buyer makes a purchase is 0.9. Find the average interval between buyers who left without a purchase.

Task 11. A state graph is given that describes the operation of the system.

Given the intensity of transitions on the state graph, write the Kolmogorov equations for state probabilities at an arbitrary instant of time and the equivalent system of equations for the Laplace transforms. Find stationary probabilities. Problem 12. A simple stream of intensity 1 requirements arrives in a system with two service devices without waiting places and goes to service according to the following rule. The request is served by the first device, if it is free, by the second device, if the first is busy, but the second is free, the requirement is lost if both devices are busy at the time of its arrival. Devices have different performance. The average service time on the first device is 0.5, on the second device 0.25. Draw a graph of transition intensities, indicating what the state of the system is. Find the probability that the system is empty and that it is fully loaded (in stationary mode). Come up with a meaningful interpretation of this task.

Task 13. The audit company consistently checks four enterprises. The verification time has an exponential distribution law and is on average equal to a crescent. Enterprises are the same and independent. From past audit experience, it can be argued that with a probability of 0.4, violations in the operation of the enterprise will be detected. We introduce two random processes - the number of checked enterprises at time t and the number of checked enterprises at time t, for which violations were detected. Find the laws of distribution of these characteristics, and for t = 2 give a numerical answer.

Task 14. (continued) The auditors were divided into four equal groups, each group begins a check of its enterprise. Find the law of distribution of the number of verified enterprises at time t.

Current control in the discipline consists in certification of settlement and analytical work on topic 1, which was discussed above. If the work is successfully completed, tasks on this topic are not submitted to the final certification, but, of course, are taken into account in the student’s overall rating in the discipline. The final control in the form of a test or an examination provides for certification only on topics 2 and 3 and consists of theoretical questions and tasks. In the case of arrears on topic 1, the final certification includes material on all topics. Here is a sample list of theoretical questions.

1. Markov process with a finite state space and discrete time. State graph and probability matrix of the transition of the Markov chain.

2. The Kolmogorov-Chapman equations. Matrix of transition probabilities for a Markov chain in n steps. Calculation of probabilities of states of a Markov chain in n steps.

3. Analysis of the structure of the space of states of the chain. The main theorem of structural analysis and its consequences. Canonical numbering of chain states.

4. Regular and cyclic equivalence classes of essential chain states. A study of the equivalence class on cyclicity.

5. Classification of discrete Markov chains. Complete structural analysis of the circuit. The form of the matrix of probabilities of a chain transition with the canonical numbering of its states

6. Long-term forecast of chain evolution. Strong and weak convergence of the transition probability matrix and the state probability vector in n steps to the final transition probability matrix and the final state probability vector.

7. Ergodic theorem on the limit behavior of an indecomposable chain.

8. Long-term forecast of the evolution of the monoergodic chain ..

9. Long-term forecast of the evolution of the polyergodic absorbing chain. Search for the marginal probabilities of ruin and gain and the average marginal gain in the ruin problem.

10. Long-term forecast of the evolution of polyergodic chains of a general form. Search algorithms for the final matrix of transition probabilities and the final state probability vector.

11. Discrete Markov chains with incomes. Calculation of the total expected income.

12. Marginal behavior of the full expected income.

13. Markov process with a finite state space and continuous time. State graph.

14. The simplest stream of events. Merging and sifting of simple flows.

15. Kolmogorov differential equations for the probabilities of states of Markov chains with continuous time

16. The solution of the Kolmogorov equations for the probabilities of states of Markov chains using the Laplace transform.

17. Final probabilities of states of Markov chains with continuous time.

18. The process of pure reproduction. Calculation of state probabilities.

19. The process of pure death. Calculation of state probabilities.

20. The stationary mode of the process of death and reproduction. The final probabilities of states.

21. Queuing systems as applications of Markov processes with continuous time.

In conclusion, we note that the discipline allows for greater variability of presentation, both in depth and in volume of material. The practical orientation of illustrative examples even with serious theoretical foundations allows students to be interested in a wide range of areas of study. In addition, such a discipline is useful in the form of additional education for both technical areas of study and economic ones. The acquired knowledge and skills will find application in practical setting of tasks, in the ability to solve those systematically using universal developed methods, in making managerial decisions. We hope that the recommendations and selection of tasks will be useful not only to students, but also to everyone who is interested in Markov processes and their management.

Antoniou I., Bosco F. (2000) On the spectral properties of a Markov model for       learning processes, International Journal of Modern Physics  , vol. 11., No 2, pp. 213-220.

Casas J.M., Ladra M., Rozikov U.A. ( 2019) . Markov processes of cubic stochastic matrices: quadratic stochastic processes . Linear Algebra and its Applications, vol. 575, pp. 273-298.

Demin S. S., Dombrovskaya E. N., Mushrub V.A., Shichiyakh R. A., Gaponenko T. V. (2018). Essence and the impact of risks and uncertainties in the investment-related decision-making process. Espacios, vol. 39, No. 31, pp.13-21

Frank T.D. (2003) A note on the Markov property of stochastic processes described by nonlinear Fokker-Planck equations, Physica A: Statistical Mechanics and its Applications, vol. 320, pp. 204-210.

Gao F., Wang Q. (2003 ) Upper bound estimates of the Cramer functionals for Markov processes”, Potential Analysis, vol. 19, No 4, pp. 383-398.

Howard R.A. (1977), Dynamic programming and Markov processes. Moscow , Soviet radio, p.488

Kemeni D. D.  , Snell D. L. (1970) Finite Markov chains., Moscow, Science, p.272

Kleinrock L. (1979) Quеueing systems , Moscow , Mechanical engineering, p.432

Kolmogorov A. (1931) Uber die analytischen methoden in der wahrscheinlichkeitsrechnung  Mathematische Annalen. vol. 104, p. 415.

Muhly P.S., Solel B. (2002 ) Quantum Markov processes (correspondences and dilations)  , International Journal of Mathematics,, vol. 13, № 8, pp. 863-906.

Popov V.A., (2018),  Inflation and consumer basket . Journal of Reviews on Global Economics , vol . 7, No. Special Issue , pp. 453-456.

Serfozo R.F.  (2005), Reversible Markov processes on general spaces and spatial migration processes. Advances in Applied Probability. vol. 37,No  3, pp. 801-818.

Sokolov G. A ., Chistyakova N.A.( 2005) Probability theory. Managed Markov chains in        Economics. Moscow, Fizmatlit,  248р.

Sukhorukova I.V., Chistyakova N.A. (2018). Methodical Aspects of Actuarial Mathematics Teaching .  Astra Salvensis, Vol.VI , Special Issue,  pp. 847-857.

Sukhorukova I.V, Chistyakova N.A., (2018), Economic regulation and mathematical modeling of insurance product cost,  Journal Regional Science Inquiry, Vol. X (2), pp. 195-203

Sukhorukova I.V, Chistyakova N.A., (2019) Insurance of the termination risk of projects with joint companion activity., Journal of Reviews on Global Economics.  vol. 8, pp. 269-274.

Sukhorukova I.V., Chistyakova N.A. (2018) Optimization of the Formation of the Capital Structure of the Insurance Company, Taking into Account the National Specifics of Insurance. Journal of Reviews on Global Economics. Vol. 7, pp. 146-1

Sukhorukova I.V. , Fomin G.P. , Ekareva I.L. , Mushrub V.A. (2019) Hybrid Method for Multi-Criteria Risk  Minimization.  Espacios  Vol. 40,  No 34, p. 14. Retrieved from: https://revistaespacios.com/a19v40n34/19403414.html

1. Doctor of Economic Sciences, Professor of the Department of Higher Mathematics,Plekhanov Russian University of Economics,  Russian Federation Email: suhorukovaira@yandex.ru

2. Candidate of Science in Physics and Mathematics, Associate Professor of the Department of Higher Mathematics, Plekhanov Russian University of Economics,  Russian Federation Email: chistna@mail.ru