ISSN 0798 1015

Vol. 41 (Nº 07) Año 2020. Pág. 1

Aplicación de DEA en el análisis de la eficiencia del proceso de fabricación de puertas de una empresa metalmecánica en Colombia

Application of DEA in the analysis of the efficiency of the door manufacturing process of a metalworking company in Colombia

FERNANDEZ, Sergio A. 1; CAMPO, Emiro A. 2 y PALACIO, David 3

Recibido: 27/03/2019 • Aprobado: 14/02/2020 • Publicado 05/03/2020

Contenido

1. Introducción

2. Metodología

3. Resultados

4. Discusión

5. Conclusiones

Referencias bibliográficas

1. Introducción

Actualmente las empresas buscan mejorar cada vez más sus procesos para lograr niveles de eficiencia que les permita mantener productos competitivos y crecer en el mercado (Fuchs y Schreier, 2011). Es preciso aclarar, que el control de estos procesos requiere de una medición que abarque cada una de las variables que puedan influir en las salidas (productos), siendo un punto de partida pertinente para proponer soluciones integrales que contribuyan al mejoramiento de los mismos (Azadi et al., 2014), por lo que se hace necesario la utilización de metodologías y herramientas que permitan realizar el análisis tanto de la información de entrada como de los resultados (Cano, Campo y Gómez, 2018a).

La investigación que soporta este artículo se basó en el proceso de fabricación de puertas en una industria metalmecánica de Colombia, debido a que los tiempos de producción y la calidad del producto se están viendo afectados como consecuencia de la baja eficiencia de los procesos que se requieren para elaborarlos, motivo por el cual, resulta pertinente la aplicación de la técnica no paramétrica Análisis Envolvente de Datos (DEA) para que a partir de los resultados obtenidos se pueda formular un plan de mejoramiento respectivo. El análisis tradicional de la eficiencia de los procesos en las empresas es realizado por medio de indicadores que finalmente son cocientes, y pueden llevar a tomar decisiones poco acertadas, ya que estos son medidas puntuales y determinísticas que presentan limitaciones para inferir sobre tendencias o comparar entre empresas de naturaleza similar (Valencia y Restrepo, 2016). Mediante la aplicación de la herramienta DEA se pretende identificar cuáles de los procesos son los responsables del incremento en tiempos de producción, permitiendo así, intervenir como primera medida de mejora aquellos que están afectando con mayor impacto el rendimiento de la operación debido a su ineficiencia.

En esta investigación se tomó al análisis envolvente de datos , dado su enfoque basado en la programación lineal, usado para evaluar la eficiencia relativa o el rendimiento de las unidades de toma de decisiones (o DMU por sus siglas en inglés), donde las DMU que alcance la frontera de eficiencia  (Score =1) se consideran eficientes y las que no alcance esta frontera (Score < 1) se consideran ineficientes (Charnes, Cooper y Rhodes, 1978). Esta técnica es una herramienta no paramétrica, ya que, el modelo no requiere una hipótesis sobre la distribución de los datos de estudio (Sekhri, 2011) y las medidas que arroja el modelo se clasifican como entradas o salidas del sistema, las cuales son seleccionadas de acuerdo al caso de estudio. DEA permite además estimar la eficiencia de la producción entre los procesos internos o entre varias empresas de características similares, evaluando el rendimiento con base en múltiples criterios para permitir a las organizaciones probar sus suposiciones de la productividad y la eficiencia de sus operaciones (Sherman y Zhu, 2013).

Para este caso se implementó en primera instancia un modelo básico de DEA enfocado a las salidas, sobre lo cual, se observó si las DMU presentaban escala de retorno constante (CCR)Charnes et al., 1978) o escala de retorno variable (BBC) (Banker, Charnes y Cooper, 1984). Este aspecto se definió mediante la observación y comparación de las variables entre las diferentes DMU, llegando a la conclusión de que era apropiado implementar un modelo de escala de retorno variable orientado a las salidas (BBC-O), dado que no eran homogéneos los valores presentados.

Además, se implementó un modelo especial del DEA como lo es la región de seguridad (Assurance Region - AR) (Thompson, Langemeier, Lee, Lee y Thrall, 1990), con la intención de analizar la eficiencia de las unidades de toma de decisiones (DMU) según la posición en la frontera de la región de seguridad (Farrell, 1957).

Es así como este artículo, hace hincapié en la aplicación de este modelo DEA “Assurance Region” (AR) para disminuir la aparición de valores de cero en los pesos ponderadores que genera el modelo al momento de hallar las eficiencias de cada DMU mediante su respectivo modelo de Programación Lineal y así, encontrar cuál de las DMU seleccionadas es la que menos eficiencia refleja en la industria metalmecánica objeto de estudio involucrando todas sus variables. Lo anterior, se logra mediante la asignación de unos límites inferiores y superiores para darle peso a las entradas del proceso y restringir el modelo a una región menor (Aristizábal, Castro, Echeverri y Valencia, 2017).

Para la asignación de dichos límites se toman dos de las variables de estudio y se relacionan entre sí a través de sus pesos ponderadores estableciendo un ratio en el cual, el modelo asignará los valores de sus pesos ponderadores. Es así, como Cooper, Seiford y Tone (2007) plantean la ecuación 1.

Donde, v1 y v2 representan los pesos ponderadores de las variables 1 y 2 respectivamente y los límites inferior y superior en que se puede asignar su relación están representados de L1,2 y U1,2 respectivamente. Por ejemplo, si se tiene la restricción donde la variable “Operarios” debe tener una relación en sus pesos ponderadores igual o hasta dos veces más importante que la variable “Máquinas”, la restricción de sus pesos quedará tal como se presenta en la ecuación 2.

A esto se le conoce como una zona de seguridad, donde el objetivo es evitar la aparición de ceros en sus pesos ponderadores, ya que, esto indica que aquella variable que presente valor de cero en su peso ponderador es muy débil y ha sido anulada en el cálculo de la eficiencia, lo cual, para este caso no resulta apropiado puesto que las eficiencias serán parciales y no se podría determinar la eficiencia real de la DMU analizada.

1.1. Antecedentes

La medición de la eficiencia se remonta a los estudios de Koopmans (1951), donde se menciona por primera vez el concepto de eficiencia técnica. Luego autores como Farrel y Fieldhouse (1962) y Farrell (1957) realizan una aproximación cuantitativa de la eficiencia y comparan unidades o criterios de toma de decisión entre sí, de modo que este concepto deja de pensarse como algo absoluto, y toma un valor relativo respecto al entorno en el que se esté analizando.

Años más tarde, Charnes et al. (1978) introducen la técnica no paramétrica DEA, basada en la programación lineal, con el objetivo de medir la eficiencia relativa de las unidades de toma de decisiones (Hatami-Marbini y Toloo, 2017), usando modelos con múltiples entradas y salidas. A partir de este momento, comienzan a adelantarse estudios mediante esta técnica e inicialmente se le dan dos enfoques que son el CCR (Stancheva y Angelova, 2008) y el BCC (Banker et al., 1984). El modelo CCR, calcula la eficiencia de las DMU bajo una escala de retorno constante (Hu y Liu, 2015), por su parte el modelo BCC, agrupa en diferentes escalas de retorno variable, según las características de las unidades de toma de decisiones.

DEA comenzó a ser usado en diferentes campos y ante las diversas situaciones fueron surgiendo modelos más complejos como el AR (Assurance Region), permitiendo definir pesos en los límites inferior y superior, para restringir así el valor de las variables. Este modelo resulta de gran utilidad en los casos donde las variables están sujetas a predeterminadas relaciones (Thompson et al.,1990; Thompson, Singleton, Thrall, & Smith, 1986).

En cualquier estudio organizacional, evaluar la eficiencia es necesario para entender el estado de los procesos y poder intervenir de acuerdo a las necesidades encontradas, y también es muy importante poder comparar el estado de la empresa con respecto a las demás del sector. La metodología DEA pretende ser una herramienta que evalúa el rendimiento de unas DMU con respecto a la más eficiente de la muestra seleccionada (Cook, Tone y Zhu, 2014), y así poder proyectar mejoras en las salidas o disminuir recursos en las entradas, teniendo como referente la DMU eficiente.

La técnica DEA ha sido implementada en diversos temas a nivel mundial. Algunos de los sectores que comenzaron con su implementación y en los cuales ha habido avances más significativos, es el sector de la medicina (Hollingsworth, Dawson y Maniadakis, 1999). En las universidades se ha usado para evaluar la eficiencia de los planes de estudio (Villarreal y Tohmé, 2017). Otros autores han enfocado sus estudios a problemas ambientales y a las eficiencias de los biocombustibles (Gómez, 2016; Kang, Xie, Wang y Wang, 2017). Además, se ha aplicado la metodología en la fase de exploración de algunos proyectos mineros (Kauppinen y Khajehzadeh, 2015; Kauppinen, 2016) y en el estudio de la selección de mercados de exportación (Cano, Campo y Baena, 2017), entre otros.

Zhou, Yang, Chen y Zhu (2017), realizan un estudio de revisión bibliográfica de la aplicación de DEA en el tema de desarrollo sostenible y clasifican parte de su investigación por sectores, dejando en evidencia que aproximadamente el 22% de los estudios realizados durante 1996 y 2016 son aplicados a la industria manufacturera, mientras que el 63% de los estudios se realizaron en temas forestales, de agricultura, de pesca, entre otros. Además, la mayor parte de los estudios usan los modelos básicos (CCR y BCC), mientras que un porcentaje menor implementan modelos especiales.

Algunos modelos AR han sido aplicados para evaluar una localización eficiente de granjas (Thompson et al., 1990) y de estaciones de metro (Wey, 2015). Otros autores han aplicado estas restricciones para comparar aeropuertos, de modo que permita identificar la eficiencia real de estos (Lai, Potter, Beynon y Beresford, 2015). En este caso, la aplicación de los  modelos DEA en empresas manufactureras  logra establecer la eficiencia real de la empresa y de los procesos involucrados en la fabricación de los diferentes productos,   y de esta forma crear planes de mejora continua en los procesos menos eficientes.

Debido a la cantidad de reprocesos y de retrasos en la producción de puertas en la empresa metalmecánica localizada en el departamento de Antioquia (Colombia), se hizo necesario realizar un estudio que permitiera identificar de manera precisa, cuál de los procesos es el más ineficiente, a fin de intervenir inicialmente allí en procuras de obtener mejoras en los tiempos de producción de los demás procesos.

La investigación es de tipo cuantitativo y descriptivo, ya que mediante la herramienta DEA se analiza la eficiencia de cada proceso y se estiman posibles mejoras, de este modo se selecciona cuál es el modelo DEA más pertinente para el caso de estudio. Además, para poder cuantificar las DMU, se hizo necesario realizar un trabajo de observación directa de cada operación, durante el cual se tomaron algunas variables como los tiempos, cantidades de insumos y salidas entre cada proceso. La metodología empleada consta de 3 etapas: Identificación y selección de los parámetros del modelo; recolección de la información y orientación del modelo DEA; y ejecución del modelo

2.1. Identificación y selección de los parámetros del modelo

La fabricación de puertas en la empresa consta de diversos procesos que varían de acuerdo al tipo o referencia que se esté produciendo, sin embargo, hay 11 procesos que siempre están en todas las referencias. Debido a esto, las DMU usadas para desarrollar el modelo fueron los 11 procesos que se presentan en su respectivo orden de ejecución en la tabla 1.

Tabla 1
Unidades de toma de decisiones
seleccionadas para el modelo DEA

Cada una de estas actividades son necesarias para elaborar una puerta, y esencialmente, constan de mano de obra calificada y de puestos o máquinas de trabajo en los cuales se llevará a cabo la operación requerida para darle continuidad al flujo del proceso. Para elegir las entradas y las salidas del modelo, se llevó a cabo una revisión de cada proceso, se analizó el flujograma del proceso y, debido al carácter cuantitativo del estudio, se tomaron como variables de entrada el número de máquinas por proceso y el número de personas involucrado directamente en cada uno de estos. Como variable de salida se seleccionan las unidades producidas por hora en cada proceso. Para dicha elección de las variables se tuvo en cuenta que las de entrada debe de reunir todos los recursos que influyan en las salidas, y, a su vez las salidas, deben de abarcar todos los resultados útiles, con los cuales se pretende evaluar las DMU seleccionadas (Fernández & Quesada, 2015).

Tabla 2
Variables de entrada (I) y de salida (O)
propuestas para el modelo DEA

2.2. Recolección de la información y orientación del modelo DEA

La información para cada variable fue obtenida a través de la observación directa de cada proceso en diferentes intervalos de tiempo de cada turno laboral y en distintos días de la semana, de este modo se evita algún sesgo en la toma de datos. También se comparó la información recolectada con los registros de producción que cada operario lleva en su puesto de trabajo. Por último, se realizaron entrevistas con expertos y de este modo se logra alimentar el modelo con los diferentes datos obtenidos.

El objeto de estudio va enfocado al aumento de salidas (unidades producidas por hora), por lo tanto, la formulación del modelo va orientada hacia las salidas.

2.3. Ejecución del modelo

El software empleado para la realización del estudio fue DEA-SOLVER-PRO versión V.9.0, generado por la firma SAITECH, empresa dedicada a realizar herramientas de optimización y sistemas de soporte para la toma de decisiones. Inicialmente se implementó el modelo BCC-O, dado que el comportamiento de cada variable al interior de cada proceso (DMU) era variable y el modelo debía contemplar este aspecto al momento de calcular las eficiencias respectivas. Luego, al analizar los resultados obtenidos con base en la ponderación de pesos, se logra observar que las eficiencias obtenidas eran parciales, dado la presencia de pesos ponderadores con valor de cero, por lo tanto, se implementó el modelo Assurance Region Variable Output Oriented (AR-O-V) en busca de eliminar la aparición de “ceros” en dichos pesos ponderadores. Cabe resaltar que estos modelos en su planteamiento matemático se trabajaron con los modelos duales de programación lineal que se enfocan en los pesos ponderadores, puesto que, uno de los objetivos del análisis era hallar las eficiencias de las DMU con la inclusión de todas las variables, es decir, que no se podía aceptar pesos ponderadores con valor de cero. Es así, como el modelo dual del BCC-O se plantea de manera generalizada en la ecuación 3:

Donde vi y ur representan los pesos ponderadores de las variables de entrada y de salida que serán encontrados, xi y yr representan los valores de las variables de entrada y de salida y v0 representa el peso asignado por la restricción de convexidad, dado que es un modelo de escala de retorno variable (Cook y Zhu, 2008).

Luego de ejecutar el modelo de escala de retorno variable enfocado a las salidas BCC-O para observar qué impacto tendría en el comportamiento general de las eficiencias y analizar el comportamiento de los pesos ponderadores, se obtuvieron los siguientes resultados:

Tabla 3
Resultado de la eficiencia del modelo BCC-O en los procesos para
la fabricación de puestas de distintas especificaciones técnicas

-----

Tabla 4
Ponderaciones de los pesos variables de entrada (I)
y de salida (O) propuestas para el modelo BCC-O

En la tabla 3 se observa que el único proceso que alcanza la frontera de eficiencia es el de “Empaque” (Score = 1) y los demás son ineficientes (Score <1) y requieren mejoras, pero es el proceso “Soldadura” el que requiere mayor intervención ya que es el más ineficiente (menor score).  La letra E que aparece al lado de algunos valores de la tabla 4, muestra el número en notación exponencial, sustituyendo parte de este por E+n, donde “E” multiplica al número anterior por 10 a la n. Al analizar las ponderaciones de los pesos en la tabla 4, se puede observar la presencia de ceros en todas las DMU de la variable “Operarios” y en algunas DMU de la variable “Máquinas”, lo cual indica que la variable “Operarios” es muy débil e implica que el modelo aún no se ajusta a la realidad de la empresa, y que sus eficiencias no son confiables mientras que los ceros en los pesos ponderadores aparezcan.

Dado los resultados obtenidos, es necesario proceder a implementar modelos más especializados, en los cuales se imponen ciertas restricciones, con la finalidad de anular la aparición de ceros en los pesos de las variables y de esta manera determinar la eficiencia de los procesos (DMU´s) incluyendo todas las variables de estudio.

Como se mencionó anteriormente, uno de los modelos especiales para tal fin, es el AR y para este caso se implementó el “AR-O-V”, dado que se busca determinar la región de seguridad que evite la aparición de ceros en los pesos ponderadores y que contemple la restricción de escala de retorno variable, ya que, se identificó que los procesos no son homogéneos entre sí por sus valores en cada una de sus variables.

Para lo anterior, se hizo un análisis con el jefe de producción de la compañía, con el cual se tomó la decisión de asignarle el nivel de importancia mostrado en la tabla 5 a las variables de estudio, dado los costos de operación. Es así como, la variable “Operarios” presenta un nivel de importancia igual o hasta dos veces más que la variable “Máquinas” y que la variable “Unidades Producidas”.

Tabla 5
Límites para
las variables

Fuente: elaboración propia

Con base en ello, al modelo dual de programación lineal presentado en la ecuación 3 se la adicionaría las siguientes restricciones de la ecuación 4 y 5.

Al ejecutar nuevamente el modelo con las restricciones adicionales se construye la tabla 6.

 donde se muestra las eficiencias del sistema productivo calculadas mediante el modelo AR-O-V.

Tabla 6
Eficiencias del sistema productivo
calculadas mediante el modelo AR-O-V

En los resultados que se muestran en la tabla 6 se observa que el proceso de “Empaque” sigue siendo el más eficiente y que el resto de procesos requieren mejoras para que alcancen la frontera de eficiencia. En este caso el proceso más ineficiente (menor valor del Score)  es el de “Soldadura”, seguido del proceso de “Pulido”.

Además al analizar los resultados de las ponderaciones de los pesos en la tabla 7 se puede observar que finalmente en este escenario, los pesos de las variables no dan cero, lo cual brinda confianza para el modelo, ya que incluye todas las variables en los cálculos de las eficiencias. 

Tabla 7
Ponderaciones de los pesos variables de entrada (I)
y de salida (O) propuestas para el modelo AR-O-V

Dado los resultados obtenidos en este escenario, se selecciona el modelo AR-O-V como el indicado para estudiar la situación de la empresa. En la figura 1 se muestran los diferentes procesos (DMU), las eficiencias obtenidas con el modelo AR-O-V; además se muestra la clasificación por eficiencia de los procesos, donde los procesos clasificados como “Eficientes” son aquellos cuya eficiencia (Score) corresponde a 1, los procesos clasificados como “No eficiente moderado” son los que están en un rango de 0,8-0,99, y por último, los procesos llamados “No eficiente crítico” son los que obtuvieron una eficiencia menor a 0,8.

Figura 1
Eficiencia y clasificación por eficiencia de los
procesos (DMU) obtenidas con el modelo AR-O-V

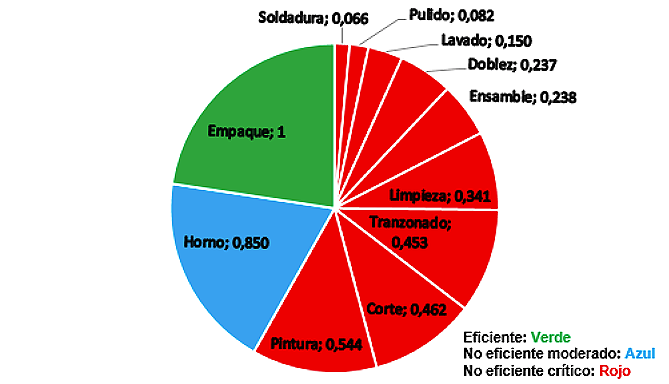
En la figura 1, se observa que solo el proceso (DMU) clasificado como “Eficiente” es el “Empaque” y que el proceso “Horno” se clasifica como “No eficiente crítico”, por lo que este proceso requiere una mayor intervención, ya que tiene mayor impacto negativo en el rendimiento de la operación, y se debe mejorar con el fin de aumentar la eficiencia en la fabricación de puertas.

Inicialmente, el jefe de producción y las personas a cargo de los procesos de la compañía sugerían antes de la realización del estudio que el proceso más ineficiente era el de “Pintura”, dado que en ocasiones era necesario retocar las puertas y  solo contaban con un puesto de trabajo para esta actividad, sin embargo, una vez realizado el estudio DEA, queda en evidencia que realmente el proceso al cual debe dirigirse una  primera medida correctiva a fin de que  la operación sea más eficiente, es la “Soldadura”, cuya eficiencia obtenidas con el modelo AR-O-V es la más distante cuantitativamente de 1 .

A pesar de que el modelo muestra que la “Soldadura” junto con el “Pulido” son los procesos más ineficientes, es posible que, una vez solucionado el problema en el proceso de soldadura, el pulido pase a alcanzar su frontera de eficiencia, ya que este proceso es afectado directamente en tiempo debido a la gran cantidad de puntos de soldadura que se deben retocar.

La implementación de la técnica DEA es conveniente para este tipo de empresas, en las cuales tradicionalmente han medido la eficiencia de las operaciones mediante indicadores aislados, pues al aplicar estos estudios, deja en evidencia que realmente los procesos que requieren intervención como primera medida, no son necesariamente los que dichos indicadores están mostrando porque no se evalúan de una manera integral.

Adicional a esto, resulta de bastante utilidad usar desde los modelos básicos de DEA hasta los especiales, ya que, al ir analizando el comportamiento de cada modelo se logra ir mejorando el análisis volviéndolo más confiable para la toma de decisiones.

Con base en el estudio presentado, es posible observar que la técnica DEA trae consigo diversos modelos que se pueden adaptar a varios escenarios, permitiendo ajustar la herramienta según sea la necesidad del sector al que vaya dirigido el estudio.

La utilidad de la técnica es importante en la fase de diagnóstico para poder identificar verdaderamente cuál es el proceso que está siendo ineficiente y poder llevarlo a la frontera de eficiencia con un plan de mejora pertinente. En este caso se puede considerar que el 81% de los procesos son ineficientes, y que solo el 19% de los procesos presentan niveles altos de eficiencia.

Para mejorar la eficiencia operacional en la fabricación se puertas se hace necesario intervenir el proceso de “Soldadura”, y luego volver a realizar el análisis de eficiencia de los procesos y así determinar el proceso más crítico nuevamente. Este proceso de mejora continua es fácil ya que una vez diseñado el modelo DEA para este problema solo se debe actualizar los datos.

Para este caso, resulta novedoso aplicar la técnica a una industria metalmecánica y poder determinar mediante un modelo AR cuál de los procesos es el más ineficiente. Aunque es un primer paso para mejorar todo el proceso de producción; intervenir adecuadamente este proceso hasta alcanzar su frontera de eficiencia permitiría a la compañía obtener un mayor nivel de eficiencia real y de este modo ir mejorando cada actividad según los resultados obtenidos en el modelo.

Aristizábal, D., Castro, M. Y., Echeverri, P. A., & Valencia, J. D. (2017). Assessing the efficiency of science, technology and innovation using Data Envelopment Analysis (DEA): The case of Colombia. DYNA (Colombia), 84(202), 215–220. https://doi.org/10.15446/dyna.v84n202.59554

Azadi, M., Jafarian, M., Farzipoor, R., & Mostafa, S. (2014). Computers & Operations Research A new fuzzy DEA model for evaluation of ef fi ciency and effectiveness of suppliers in sustainable supply chain management context. Computers and Operation Research, 54, 1–12. https://doi.org/10.1016/j.cor.2014.03.002

Banker, R., Charnes, A., & Cooper, W. (1984). Some models for estimating technical and scale inefficiences in Data Envelopment Analysis. Managment Science, 30(9), 1078–1092.

Cano, J. A., Campo, E. A., & Baena, J. J. (2017). Application of DEA in international market selection for the export of goods. DYNA (Colombia), 84(200), 376–382. https://doi.org/http://dx.doi.org/10.15446/dyna.v84n2010.63612

Cano, J., Campo, E., & Gómez, R. (2018). Simulación de eventos discretos en la planificación de producción para sistemas de confección modular. Revista Técnica de la Facultad de Ingeniería Universidad del Zulia, 41(1), 50-58.

Charnes, A., Cooper, W. W., & Rhodes, E. (1978). Measuring the efficiency of decision making units. European Journal of Operational Research, 2(6), 429–444. https://doi.org/10.1016/0377-2217(78)90138-8

Cook, W. D., Tone, K., & Zhu, J. (2014). Data envelopment analysis : Prior to choosing a model. Omega, 44, 1–4. https://doi.org/10.1016/j.omega.2013.09.004

Cook, W. D., & Zhu, J. (2008). Data envelopment analysis: Modeling Operational Processes and Measuring Productivity.

Cooper, W. W., Seiford, L. M., & Tone, K. (2007). Data Envelopment Analysis, 178.

Farrel, M. J., & Fieldhouse, M. (1962). Estimating Efficient Production Functions under Increasing Returns to Scale. Journal of the Royal Statistical Society. Series A (General), 125(2), 252–267.

Farrell, M. J. (1957). The Measurement of Productive Efficiency. Journal of the Royal Statistical Society. Series A (General), 120(3), 253–281.

Fernández, S., & Quesada, M. R. (2015). Estudio de eficiencia aplicado a productos lácteos bajo la técnica DEA. Teuken Bidikay, 07, 135–153.

Fuchs, C., & Schreier, M. (2011). Customer Empowerment in New Product Development. Jorunal of Product Innovation Management, 28(1), 17–32.

Gómez, J. M. (2016). Análisis de la variación de la eficiencia en la producción de biocombustibles en América Latina. Estudios Gerenciales, 32(139), 120–126. https://doi.org/10.1016/j.estger.2016.01.001

Hatami-Marbini, A., & Toloo, M. (2017). An Extended Multiple Criteria Data Envelopment Analysis Model. Expert Systems with Applications, 73, 201–219. https://doi.org/10.1016/j.eswa.2016.12.030

Hollingsworth, B., Dawson, P., & Maniadakis, N. (1999). Efficiency measurement of health care: A review of non-parametric methods and applications. Health Care Management Science, 2(3), 161–172.

Hu, X., & Liu, C. (2015). Managing undesirable outputs in the Australian construction industry using Data Envelopment Analysis models. Journal of Cleaner Production, 101, 148–157. https://doi.org/10.1016/j.jclepro.2015.03.077

Kang, Y. Q., Xie, B. C., Wang, J., & Wang, Y. N. (2017). Environmental assessment and investment strategy for China’s manufacturing industry: A non-radial DEA based analysis. Journal of Cleaner Production, 175, 501–511. https://doi.org/10.1016/j.jclepro.2017.12.043

Kauppinen, T. (2016). Data Envelopment Analysis as a tool for the exploration phase of mining. Computers and Geosciences, 93, 96–102. https://doi.org/10.1016/j.cageo.2016.05.005

Kauppinen, T., & Khajehzadeh, N. (2015). Sustainability in the exploration phase of mining: A Data Envelopment Analysis approach. IFAC-PapersOnLine, 28(17), 114–118. https://doi.org/10.1016/j.ifacol.2015.10.088

Koopmans, T. C. (1951). An analysis of production as an efficient combination of activities. In: Koopmans, T.C. (Ed.), Activity Analysis of Production and Allocation, Cowles Commission for Research in Economics, Monograph, Vol. 13. Willey, New York.

Lai, P. L., Potter, A., Beynon, M., & Beresford, A. (2015). Evaluating the efficiency performance of airports using an integrated AHP/DEA-AR technique. Transport Policy, 42, 75–85. https://doi.org/10.1016/j.tranpol.2015.04.008

Sekhri, V. V. (2011). A DEA and Malmquist Index Aproach to Measuring Productivity and Efficiency of Banks in India. The IUP Journal of Bank Management, 10(3), 49–64.

Sherman, H. D., & Zhu, J. (2013). Analyzing Performance of Service Organizations: Balanced Benchmarking Can Identify Best Practices That Are Often Hidden. MIT Sloan Management Review, 54(4), 37–42.

Stancheva, N., & Angelova, V. (2008). Research methodology on Data Envelopment Analysis (DEA). Florida: Universal -Publishers.

Thompson, R. G., Langemeier, L. N., Lee, C. T., Lee, E., & Thrall, R. M. (1990). The role of multiplier bounds in efficiency analysis with application to Kansas farming. Journal of Econometrics, 46(1–2), 93–108.

Thompson, R. G., Singleton, F. D., Thrall, R. M., & Smith, B. A. (1986). Comparative site evaluation for locating high energy lab in Texas. Interfaces, 16(6), 35–49.

Valencia, M., & Restrepo, J. A. (2016). Evaluación de la gestión financiera usando variables latentes en modelos estocásticos de fronteras eficientes. DYNA (Colombia), 83(199), 35–40. https://doi.org/10.15446/dyna.v83n199.54612

Villarreal, F., & Tohmé, F. (2017). Análisis envolvente de datos. Un caso de estudio para una universidad Argentina. Estudios Gerenciales, 33(144), 302–308. https://doi.org/https://doi.org/10.1016/j.estger.2017.06.004

Wey, W. M. (2015). Smart growth and transit-oriented development planning in site selection for a new metro transit station in Taipei, Taiwan. Habitat International, 47, 158–168. https://doi.org/10.1016/j.habitatint.2015.01.020

Zhou, H., Yang, Y., Chen, Y., & Zhu, J. (2017). Data envelopment analysis application in sustainability : The origins , development and future directions. European Journal of Operational Research, 264, 1–16. https://doi.org/10.1016/j.ejor.2017.06.023

1. Facultad de Administración, Politécnico Jaime Isaza Cadavid, Colombia. Ingeniero Industrial, Magister en Investigación  operativa y estadística. safernandez@elpoli.edu.co

2. Facultad de Ingeniería, Universidad de Medellín, Colombia. Ingeniero Industrial, Magister en Ingeniería Industrial. ecampo@udem.edu.co

3. Facultad de Administración, Politécnico Jaime Isaza Cadavid, Colombia. Ingeniero de Productividad y Calidad. david_palacio92121@elpoli.edu.co