

 Vol. 41 (Nº 06) Año 2020. Pág. 24
Vol. 41 (Nº 06) Año 2020. Pág. 24
VILLARRAGA, Beatriz A. 1; ROJAS, Osvaldo J. 2 y SIGARRETA, José M. 3
Recibido: 20/11/2019 • Aprobado: xx/02/2020 • Publicado: 27/02/2020
RESUMEN: Se implementa una metodología sustentada en un modelo didáctico, que permite formar conceptos asociados a las funciones de variable compleja en estudiantes universitarios de la licenciatura en matemática. Dicha metodología propicia imbricar la formación de conceptos, según las etapas propuestas por Galperin (1956) y la resolución de problemas de Polya (1965); mediante un sistema de actividades, establecido en cuatro fases. La aproximación es en forma de “espiral”, donde cada concepto subordinado, colateral y superior, alcanza grados de complejidad más avanzados. |
ABSTRACT: A methodology based on a didactic model, that is conductive to forming associated concepts to complex variable functions in college students is implemented This methodology promotes the imbrication of concept learning according to the stages proposed by Galperin (1956) and problem solving posed by Polya (1965); this through a system of activities stablished in four phases. Approach is in form of a “spiral”, where each subordinate, lateral and superior concept reaches higher degrees of complexity each time. |
Aprender a conocer, a hacer, a convivir y a ser, constituyen pilares básicos del aprendizaje que la educación debe crear y desarrollar (Delors, et al., 1997). En el proceso de enseñanza-aprendizaje de las matemáticas en el aula, la formación de conceptos matemáticos, en general, y la resolución de problemas, en particular, contribuyen a favorecer el desarrollo de dichos pilares.
Las Investigaciones de Tall y Vinner (1981), Sfard (1991), Duval (1999), entre otros, han sentado las bases para una teoría sobre la formación de los conceptos matemáticos, basados en la relación entre la definición de concepto y su imagen. En esas investigaciones se pone de manifiesto la necesidad de presentar actividades que permitan el paso entre los distintos sistemas de representación dentro del proceso de enseñanza aprendizaje de la construcción de los conceptos matemáticos (Duval, 1999). Por su parte, D’Amore (2001) asevera que no sólo a través de múltiples representaciones se logra el aprendizaje de un concepto, sino que además se necesita de la lógica.
En relación a la resolución de problemas, es de destacar que: Polya (1965), Falk (1980), Schoenfeld (1985, 1987, 1994), Sigarreta, Rodríguez y Ruesga (2006), Santos (2007), Cai & Nie (2007), Sriraman y English (2010), Pochulu y Rodríguez (2012), Parra & Breda (2017), entre otros, enriquecen la investigación, pues establecen que el uso iterativo de tecnicismos, como algoritmos, palabras claves, procedimientos, definiciones y memoria del estudiante, predomina sobre el tratamiento de los conceptos, hecho que impide el planteamiento, análisis y solución de problemas.
Fischbein (1990) establece algunas líneas generales que se pueden desarrollar en torno a la formación de conceptos, en particular, expone un conjunto de indicaciones para el tratamiento de problemas relacionados con conceptos matemáticos, tales como: el infinito actual y potencial, y números complejos, entre otros. Por otra parte, Falk (2015) asevera que:
… en lo concerniente a un concepto matemático el aprendizaje es un proceso de construcción de significado del concepto. El proceso de construcción pasa por etapas donde el significado es construido… El proceso de construcción de significado se desarrolla en la actividad de la solución de problemas, cada problema nuevo contribuye a mirar el concepto en un nuevo contexto que enriquece su significado... y permite establecer las relaciones que cumple el concepto con otros conceptos (p. 6).
Santiesteban y Rodríguez (2004) establecen métodos de trabajo en el aula, a través de unidades didácticas o sistemas de actividades que según se asevera, permiten facilitar el proceso de enseñanza-aprendizaje haciendo uso de la resolución de problemas para la formación de conceptos. Duke, Dwyer, Wilhelm y Moskal (2008), se enfocan en el significado de los conceptos de función de variable compleja, sus dificultades, solución de problemas y representaciones.
A través, de la aplicación de métodos empíricos como la observación en clase, encuestas a los estudiantes y la experiencia de los investigadores, se pudo constatar las siguientes insuficiencias: son limitados los conocimientos previos que poseen los estudiantes, son mínimos los sistemas de representación que se dan a conocer por parte del docente, es limitado el empleo de métodos que induzcan a la actuación productiva de los estudiantes, las actividades asignadas en el aula no propician la experimentación, búsqueda y exploración. En particular, respecto a la construcción del concepto de función de variable compleja, no se introduce a partir de los conocimientos existentes y de las experiencias acumuladas en la práctica, y se desconoce una adecuada metodología para la integración, entre la resolución de problemas y la formación de conceptos matemáticos.
Para lograr los objetivos se implementó un sistema de actividades orientado a la construcción del concepto de unidad imaginaria, representaciones de los números complejos, operaciones, potenciación, raíces, lugar geométrico y funciones de variable compleja. Cada una de estas actividades se establece bajo las cuatro fases que conforman la etapa de integración a saber: motivación, adquisición, elaboración y fijación-aplicación.
El marco teórico en que se enfoca la investigación se explica en la siguiente sección. A continuación, se explica la metodología de investigación. Para finalizar se presentan los resultados obtenidos de la Metodología para la formación de conceptos asociados con las funciones de variable compleja y la discusión de estos.
Desde el punto de vista filosófico se asume la concepción dialéctica (Afanasiev, 1979) y en el orden psicopedagógico el sustento teórico está dado por el enfoque histórico-cultural de Vigotsky (1988) y sus seguidores. Esencialmente, se asume la zona de desarrollo próximo (ZDP), la cual, puede ser entendida como la diferencia entre el nivel de desarrollo real o zona de desarrollo actual, determinada por el conjunto de actividades que el sujeto puede hacer por sí mismo, sin recurrir más que a sus conocimientos previos, y sin la ayuda de alguien que posea mayor conocimiento o información en relación al problema o tema; con el nivel de desarrollo potencial o zona de desarrollo potencial, que está determinado por el nivel de conocimientos que el sujeto podría alcanzar al interactuar con los medios de instrucción de la sociedad o la ayuda de otras personas expertas en el tema.
Dentro de los elementos metodológicos asociados a la formación de conceptos matemáticos, se considera que los conceptos no se forman en el ser humano de manera inmediata, sino que son el resultado de un proceso que puede estructurarse, para su estudio en niveles: Análisis-Abstracción, Discriminación-Identificación y Síntesis-Concreción (Ballester et al. 1992). Para el trabajo con la formación de conceptos en el aula se trabaja, en lo fundamental, con la vía inductiva y, en menor medida, con la vía deductiva, sin dejar de lado para los autores, una vía mixta que combina procesos inductivos y deductivos.
Existe una gran diversidad de criterios y definiciones acerca del concepto problema. Por ejemplo, las dadas por Pólya (1965), Schoenfeld (1985, 1987, 1994), Sriraman y English (2010), Cai & Nie (2007), entre otros. En esta dirección se asume lo planteado por Campistrous y Rizo (1996: 9) al expresar que un problema es:
… toda situación en la que hay un planteamiento inicial y una exigencia que obliga a transformarla. La vía de pasar de la situación o planteamiento inicial a la nueva situación exigida tiene que ser desconocida y la persona debe querer realizar la transformación.
Así mismo, se comparte el criterio de Pérez (2004: 1), respecto a los problemas retadores, cuando plantea que: «… invitan al estudiante a pensar autónomamente, a indagar, a cuestionar, a razonar y a explicar su razonamiento».
Por su parte Falk (2001) afirma que un problema retador propicia en el estudiante establecer redes o mapas conceptuales cada vez más enriquecidos. Los problemas retadores generan motivación e interés en los estudiantes, pues tienen tres características especiales, al ser una situación «… que estimula el pensamiento, que sea interesante para el alumno, y que la solución no sea inmediata» (Falk, 1980: 16).
En relación al proceso de resolución de problemas se asume las fases propuestas por Pólya (1965): orientación hacia el problema, trabajo en el problema, solución del problema, evaluación de la solución y de la vía.
La metodología de la investigación utilizada tiene un carácter fundamentalmente cualitativo, donde se muestran los fundamentos teóricos y metodológicos asociados al proceso de enseñanza aprendizaje asociados a la formación de conceptos, a la teoría de la resolución de problemas y la constatación de una experimentación en la práctica con estudiantes de la Licenciatura en Matemáticas y Física. Se presenta un estudio de caso de tipo único, descriptivo, teniendo en cuenta que se describe la situación observada dentro del grupo de estudiantes, cuando se enfrentan a tareas enfocadas a la formación de conceptos asociados a las funciones de variable compleja a través de la resolución de problemas.
En el desarrollo de la investigación se utilizaron métodos teóricos (histórico-lógico y análisis-síntesis) y empíricos (observación participante, instrumentos de contenido, además de guías). También se utilizan los métodos estadísticos matemáticos para el procesamiento de la información obtenida, a través de los métodos y técnicas del nivel empírico, durante el desarrollo de la investigación. Este estudio se ubica en el paradigma de investigación cualitativa-interpretativa. Una de los métodos básicos, a utilizar, asociado a dicho enfoque es el estudio de casos, en lo fundamental, apoyado por la observación, interpretación y análisis de escenarios culturales naturales, para su comprensión y posterior transformación.
En la investigación participaron 13 estudiantes de quinto semestre de la Licenciatura en Matemáticas y Física de la Universidad de los Llanos, pertenecientes al curso electivo variable compleja del primer periodo del año 2016. La muestra es no probabilística, pues por ser un curso electivo, la participación de estudiantes es voluntaria, lo cual refleja la importancia educativa de la temática abordada para el desempeño profesional de los estudiantes, constatándose esto, en el aumento de la significación de los resultados en los estudiantes.
Para el trabajo en el aula se utilizan software de geometría dinámica (GeoGebra), materiales de geometría, instrumentos tradicionales, guías de trabajo, entre otros; donde las actividades establecidas permiten poner de manifiesto el proceso de formación de los conceptos asociados a las funciones de variable compleja.
En la construcción de la metodología de trabajo se tuvo en cuenta los tres niveles para la formación de conceptos propuesta por Ballester et al. (1992), que forman las categorías con las cuales se hace el análisis: (1). Análisis-Abstracción, (2). Discriminación-Identificación y (3). Síntesis-Concreción. Estas son conocidas como los niveles de desarrollo de los conceptos que dependen directamente de la actividad, es decir, de las acciones que el sujeto realiza sobre los objetos, de su experiencia, nivel de abstracción y generalización.
Cuando se lleva a cabo la acción de la metodología, para la formación de conceptos asociados con las funciones de variable compleja, es necesario establecer un proceso de integración que permite a través de un sistema de actividades la aproximación al concepto de función de variable compleja. En este se hace uso de la resolución de problemas, caracterizando los problemas con el fin que tributen a las fases de motivación, adquisición, elaboración, y fijación-aplicación, en el desarrollo de los contenidos matemáticos a tratar (funciones de variable compleja) y las funciones didácticas de la clase de matemática. Un esquema de la metodología se muestra en la figura 1.
Figura 1
Esquema de la metodología (Villarraga, 2016).
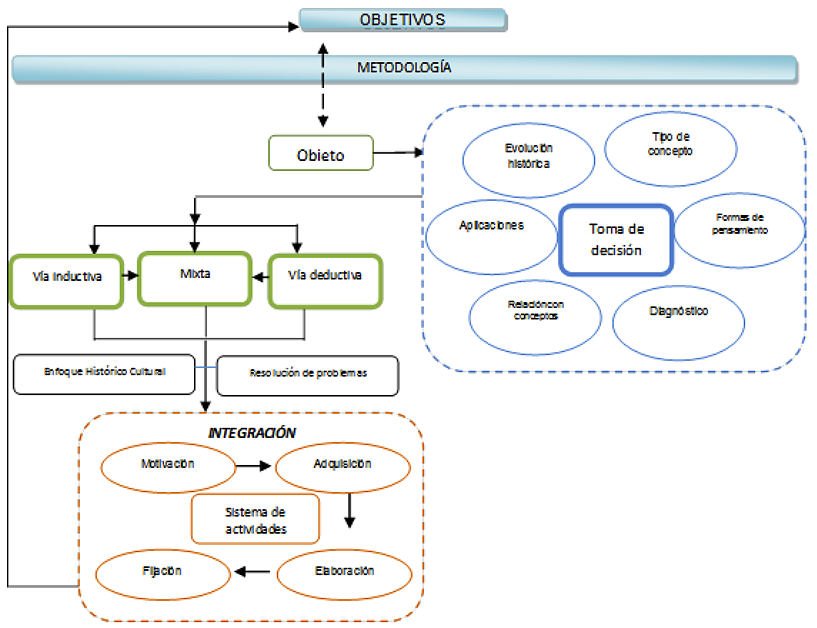
En el desarrollo de la metodología se establecen varios subprocesos, que son analizados uno a uno, con el fin de construir patrones de relación en cada uno de ellos. Dado que los objetivos de cada actividad y el sistema de control previsto, están presentes en el desarrollo de todo el proceso de enseñanza-aprendizaje, también es claro que dicho proceso está determinado por la selección del objeto matemático, que son los conceptos (subordinados, colaterales o superiores).
Para establecer las relaciones existentes entre los conceptos y poder tomar una decisión sobre la vía a seguir (inductiva, deductiva o mixta), con respecto a la instrucción, se establecen los siguientes requisitos:
De esta forma se puede establecer no sólo las relaciones conceptuales, sino que a su vez se puede llegar a determinar la vía en el proceso de enseñanza- aprendizaje del concepto, con lo cual, se da camino a construir una secuencia de acciones en la integración, que permite imbricar la resolución de problemas y las fases para la formación de conceptos. En este proceso es donde se realiza la toma de decisión como se muestra en la Figura 1.
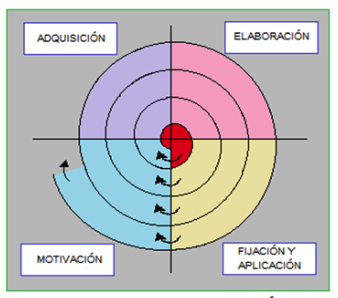
El proceso de integración posee 4 fases a saber: motivación, adquisición, elaboración, y fijación-aplicación (ver figura 2), las cuales han sido caracterizadas a través de problemas que permiten el tránsito entre ellas y un acercamiento al concepto.
Figura 2
Proceso de integración a partir de las vías
inductiva, deductiva o mixta (Villarraga, 2016)

Es de notar que, en las etapas de motivación y adquisición, para una mejor comprensión de los estudiantes en la resolución de los problemas propuestos, se puede utilizar la representación geométrica. Desde esta perspectiva, este proceso es más complejo, pues por un lado se implica mayor actividad cognitiva requerida (Arcavi, 2003; Rivera, 2011; Ramírez y Flores, 2017) y por otro, la necesidad de relacionar operaciones lógicas del pensamiento, con los procesos cognitivos de manipulación, visualización y razonamiento (Rojas, 2009; Torregrosa, Quesada y Penalva, 2010; Prior y Torregrosa, 2013; Ramírez y Flores, 2017). Este trabajo desarrollado en estas fases propicia llegar con una idea de resolución del problema acertada en la fase de elaboración.
Cada una de estas fases está orientada por dos vías principales que permiten la aproximación hacia los conceptos: la vía inductiva, donde se parte de descripciones para llegar a la definición, es decir parte de lo particular a lo general; y la vía deductiva, que inicia con la definición y a través de ejemplos de objetos se descubre el contenido y extensión del concepto, es decir se parte de lo general a lo particular. De otra parte, no se descarta el uso de una vía mixta que permite en algunas ocasiones la inductividad y la deductividad, teniendo en cuenta las características del objeto para la toma de decisiones.
De igual forma Ballester et al. (1992), no establecen en la vía deductiva la posibilidad de la aplicación como parte de la formación del concepto, situación que para los autores es necesaria, debido a los múltiples problemas a los cuales el estudiante se enfrenta de forma natural, y que permiten enriquecer el concepto en cuanto a su contenido y extensión.
El carácter dinámico de la metodología, permite construcciones y reconstrucciones entre sus componentes, estableciéndose como complementario la formación de un concepto para el acercamiento a otro nuevo. Es así, que el aproximarse a un concepto superior, sugiere una comprensión mayor de otros conceptos mediante problemas que permiten percibir y acercarse al nuevo concepto como una totalidad; tal situación se asemeja a una espiral, la cual relaciona la formación de conceptos y la resolución de problemas (ver figura 3).
Esta visión integradora de conceptos se concibe como un proceso o cambio continuo del conocimiento, en otras palabras, un devenir de los conceptos en nuevos o reconstruidos conceptos. En este devenir, el conocimiento anterior no se desprecia, sino que hace parte de las estrategias para la comprensión del nuevo conocimiento, situaciones que son usadas por el docente para lograr que el estudiante alcance niveles de conocimiento más elaborados. Desde este punto de vista la aproximación a un concepto superior, se hace de manera paulatina y permanente en forma de “espiral”, donde cada concepto subordinado, colateral y superior, alcanza grados de complejidad cada vez más avanzados. Con esta metodología se muestra que los conceptos se construyen, se van refinando y se perfeccionan en la medida en que se transita por cada uno de los niveles pasando de la Zona de Desarrollo Real a la Zona de Desarrollo Potencial.
Figura 3
Relación metodológica para la construcción de conceptos
por aproximaciones sucesivas (Villarraga, 2016)

Cada uno de estos niveles deja observar el paso de las diferentes Zona de Desarrollo Próximo, además del uso del diagnóstico como parte del proceso metodológico; el sistema de actividades como un eje que traspasa de manera ascendente a la metodología; el sistema de evaluación y control que brinda información para el mejoramiento y seguimiento de los conceptos (ver figura 3).
Figura 4
Proceso de integración desplegado
desde la metodología (Villarraga, 2016).
Cada una de las vueltas de la espiral corresponde a un objetivo dentro del proceso de aproximación al concepto de función de variable compleja; donde cada objetivo es alcanzado a partir de actividades sucesivas que permiten al estudiante a partir de problemas, relacionar conceptos entre sí y formar los conceptos en tres niveles distintos (Análisis-Abstracción, Discriminación-Identificación y Síntesis-Concreción). Aduciendo a las fases descritas anteriormente; para el proceso de integración se genera un sistema de actividades que responde a cada una de estas fases y permite cumplir los objetivos propuestos en el modelo didáctico (Villarraga, 2016).
De otra parte, la caracterización de los problemas, permiten hacer un tránsito por las diferentes fases de Pólya (1965), además de establecer los distintos momentos en los cuales el docente estará en la capacidad de ofrecer a sus estudiantes cada tipo de problema que tribute a la etapa de integración de la metodología y por ende a la formación de conceptos.
Problemas que permiten la motivación, los cuales se caracterizan por cumplir las siguientes cualidades:
Problemas que permiten la adquisición, estos se caracterizan por cumplir las siguientes cualidades:
Problemas que permiten la elaboración, estos se caracterizan por cumplir las siguientes cualidades:
• Debe dar las condiciones necesarias para pasar a la etapa de formación en el plano del lenguaje, donde los elementos de la acción deben estar representados en forma verbal (oral o escrita) por el estudiante.
Problemas que permiten la fijación – aplicación, estos se caracterizan por cumplir las siguientes condiciones:
Esta caracterización contribuye a que el docente en ejercicio, pueda establecer o seleccionar una secuencia de actividades que favorezcan el tránsito por las fases de la etapa de integración de la metodología.
Se entiende por sistema de actividades a la propuesta de acciones y operaciones relacionadas entre sí, dirigidas a favorecer el proceso de formación de conceptos asociados con las funciones de variable compleja, mediante la resolución de problemas, sin dejar de lado el desarrollo integral del estudiante. Las actividades desarrolladas se encuentran directamente relacionadas con las fases y objetivos de la metodología propuesta.
Estas actividades se estructuran en: título de la actividad, objetivo, sugerencia metodológica, motivación, adquisición, elaboración, fijación-aplicación y unas conclusiones de la actividad. A continuación, a título de ejemplo se describe una actividad, de seis propuestas.
Objetivo: Comprender el concepto de unidad imaginaria.
Sugerencia Metodológica: La siguiente secuencia de actividades, se encuentra programada siguiendo la vía inductiva, es decir, permitiéndose con ello poner a los estudiantes en situación de construir los conceptos con la ayuda de los compañeros y del profesor.
Para estructurar la información proveniente del análisis, se procedió a enumerar a los estudiantes (E1, E2, E3,…, E13) y se crearon unas escalas de valoración cualitativas basadas en la clasificación que realizan Ballester et al. y otros (1992), sobre los niveles de desarrollo de los conceptos, como se muestra a continuación en la tabla 1.
Tabla 1
Escalas de valoración cualitativas basadas en la caracterización de los niveles de
desarrollo de los conceptos mediante la resolución de problemas (Villarraga, 2016)
Nivel de solución |
Caracterización |
Análisis-Abstracción (A-A) |
El estudiante analiza los grupos o conjuntos de objetos en función de sus propiedades comunes; luego determina cuales de esas características son esenciales, forma conjuntos más complejos y elaborados, basándose en las propiedades. La caracterización permite que el estudiante determine la presencia o no del concepto superior y las relaciones existentes con otros conceptos (colaterales y subordinados) en los problemas propuestos. |
Discriminación-Identificación (D-I) |
El estudiante determina qué propiedades del nivel anterior, pueden extenderse al resto de los elementos de un conjunto, se deducen e inducen las propiedades fundamentales a la totalidad de los elementos del conjunto. Identifica el concepto como parte de la solución de un problema, donde se puede apreciar características necesarias y suficientes o aquellas en donde algunas características sean modificadas de tal manera que el estudiante compara y establece similitudes en cuanto a cada problema y la relación con el concepto. |
Síntesis-Concreción. (S-C) |
El estudiante determina las características esenciales, la estructura o el sistema de la totalidad de los elementos, donde se sintetiza el proceso y puede construir una definición. Aplica el concepto frente a problemas en nuevos contextos, donde el uso de diferentes sistemas de representación permite que el estudiante establezca las relaciones entre los conceptos superiores con los subordinados o colaterales, conduciendo a nuevos problemas en donde se pone a prueba el concepto. |
Actividad 1
Etapa de motivación, se entrega a los estudiantes una reseña histórica de los números complejos, además de algunas preguntas que relacionan los problemas históricos con la necesidad del estudio de los números complejos; adicionales a ello se presentan problemas que permiten despertar la atención y el interés por el concepto de unidad imaginaria.
Cada actividad analizada se codificó con la letra A (actividad), punto (.), el número correspondiente de la actividad 1 a la 6, punto (.), el número del problema en la actividad y punto (.); es así que el código A.1.3., hace referencia al problema 3 de la actividad 1.
A.1.1. Solucione el siguiente problema planteado por Cardano en 1545: Sea un segmento AB de longitud 10 unidades, divídelo en dos partes de tal forma que el rectángulo que se forma tenga un área de 40 unidades cuadradas. ¿Es posible construir dicho rectángulo? ¿Qué dimensiones tendría?
En el nivel de Análisis-abstracción se ubican 6 estudiantes (46,1%), los cuales no presentan dificultades en la solución, pues determinan que el rectángulo con mayor área que se puede construir es de 25 unidades cuadradas, aunque no solucionan el problema de manera algorítmica, establecen una solución y la verifican, 5 de los estudiantes (38,5%), establecen una solución algebraica haciendo uso de sistemas de ecuaciones y la ecuación cuadrática, esto se evidencia con el estudiante E3 como se muestra a continuación en la figura 5.
Figura 5
Respuesta estudiante E3
Actividad N°1 problema 1. D-I.

Etapa de adquisición, con problemas que permiten la exploración de ideas previas, estos problemas tienen el fin de establecer una primera aproximación al concepto desde el punto de vista geométrico, sobre los números complejos y el significado de i.
A.1.2. Usa el siguiente plano cartesiano, e interpreta qué significa multiplicar por -1. ¿Cómo puedes interpretar una rotación de 90°?
Los 13 estudiantes (100%) desarrollaron la actividad estableciendo que rotar 90° corresponde a multiplicar por raíz de menos uno, con lo cual se tendría que en el eje que ellos suelen llamar “y” se coloca el eje imaginario. Estas situaciones se pueden observar en la figura 6.
Figura 6
Respuesta estudiante E11
Actividad N°1 problema 2. A- A.

A.1.3. Identifica geométricamente lo que sería:

Generalice para cualquier exponente natural.
Los estudiantes establecen una relación entre la representación geométrica de los números complejos, la multiplicación por i, sus potencias y la representación algebraica de los números, sólo 3 estudiantes lograron generalizar las potencias de i cuando n es natural, otros sólo generalizaron para potencias pares e impares, pero no se percataron que las potencias pares al igual que las impares generan dos respuestas diferentes, un ejemplo de ello se aprecia en la figura 7.
Figura 7
Respuesta estudiante E2 y E11 Actividad N°1 problema 3. S-C

Etapa de elaboración, se hace referencia a problemas retos, donde se exige la interrelación de otros conceptos, procedimientos y actitudes necesarios para su resolución.
A.1.4. Observa la siguiente igualdad y determina si hay o no algún error, justifica tu respuesta:

¿Es posible esto?
Todos los estudiantes pudieron dar una razón por la cual había un error en las igualdades presentadas, sin embargo, uno de ellos se limitó a indicar el error mas no a establecer una razón o justificación del por qué sucedía que -1=1, esto se puede apreciar en la figura 8.
Figura 8
Respuesta estudiante E3 y E12
Actividad N°1 problema 4. D- I.

Etapa de fijación-aplicación, son problemas que requieren de los conceptos inter e intradisciplinarios trabajados y adquiridos en cursos anteriores, para la resolución de situaciones nuevas.
A.1.5. ¿Si se hace una rotación de 45° al vector (0,1) qué significado geométrico tiene? ¿Qué coordenadas cartesianas posee este nuevo vector?

Figura 9
Respuesta estudiante E9 Actividad N°1 problema 5. S- C.

La figura 10, presenta los resultados obtenidos por los estudiantes según los niveles de desarrollo del concepto, en cada actividad y fase. Cabe destacar que estos niveles no necesariamente necesitan de un nivel anterior en un problema para alcanzar el siguiente, por esa razón el análisis se realiza en base a las respuestas de cada problema y de las discusiones que se presentaron al interior del aula de clase.
Figura 10
Niveles de desarrollo en cada
problema. Actividad 1. exto

Al asumir la concepción dialéctica, esta ofrece al enfoque histórico-cultural de Vygotsky (1995) fundamentos psicopedagógicos de carácter teórico-práctico. Es así que el utilizar dentro del marco metodológico este enfoque, la teoría de la actividad de Leontiev (1983) y las bases de las acciones mentales propuestas por Galperin (1956); permitió enriquecer y determinar la estructura y puesta en escena de la metodología. Es de resaltar que la teoría de la Formación por Etapas de las Acciones Mentales es utilizada en diferentes asignaturas con el objetivo de favorecer el proceso de enseñanza-aprendizaje en el aula, como lo hacen Mendoza, Acevedo y Tejada (2016) para el trabajo en sus clases con el fin de lograr el concepto de Valencia Química.
La estructuración del proceso de enseñanza-aprendizaje de los conceptos asociados al de función de variable compleja hacia la búsqueda activa y dinámica del conocimiento en el estudiante, a través de un sistema de actividades, donde fundamentalmente se utiliza la tecnología, la historia de las matemáticas como recurso didáctico, la representación geométrica y procedimientos heurísticos, desde posiciones reflexivas que estimulen el desarrollo del pensamiento y la independencia cognoscitiva, pone de manifiesto que es más enriquecedor que un cúmulo de ejercicios, sin tener en cuenta el carácter dinámico y contextualizado de la enseñanza-aprendizaje de las matemáticas. La metodología sustentada en dicho sistema, favorece la formación de conceptos sobre función de variable compleja, a través de la resolución de problemas y propicia el desarrollo de los procesos lógicos del pensamiento y el dominio de los contenidos teóricos necesarios para garantizar un aprendizaje significativo.
El elemento dinamizador en la metodología se desarrolla en cuatro etapas, las cuales propician la construcción de un robusto concepto de función de variable compleja, contribuyendo a la solución del problema científico planteado. En tal dirección, se hace necesario establecer un sistema de actividades relacionado con la metodología propuesta que permite estudiar a profundidad la teoría de funciones de variable compleja desde todos los sistemas de representación sugeridos, haciendo énfasis en la representación geométrica, debido a su carácter práctico y visual, que permite mayor aprehensión por parte de los estudiantes.
El trabajo con la formación de conceptos matemáticos es importante para lograr un proceso de enseñanza - aprendizaje robusto de la matemática, en particular de las funciones de variable compleja, pues éste le propicia tratar los conceptos de objeto, de relación y de operaciones, asociados esencialmente al pensamiento abstracto, el cual está basado en conceptos, juicios y razonamientos. Los conceptos en el estudiante no se forman de manera inmediata, son el resultado de un proceso que puede estructurarse, en tres niveles: Análisis-Abstracción, Discriminación-Identificación y Síntesis-Concreción (Ballester et al. 1992; Villarraga, 2016).
Las actividades se sustentan en la teoría de la resolución de problemas, en particular los problemas retadores constituyen uno de los pilares básicos para el trabajo con la formación del concepto de función de variable compleja. La implementación de la estrategia de Pólya (1965) en el momento de resolución de cada uno de los problemas: orientación hacia el problema, trabajo en el problema, solución del problema, y la evaluación de la solución y de la vía; centrada en el apoyo de la heurística, propicia la construcción robusta de dicho concepto.
La investigación se sustenta en el paradigma cualitativo interpretativo. Los instrumentos y métodos utilizados durante el desarrollo de la investigación, permiten elaborar e implementar un sistema de actividades, para favorecer la formación del concepto de función de variable compleja.
Las actividades están estructuradas en cuatro etapas, que establecen un orden para la puesta en práctica, de manera que el proceso se hace más organizado, situación que es necesaria para un buen aprendizaje; además de ello incluye herramientas tecnológicas para la puesta en escena de las representaciones visuales de los problemas, situaciones que ponen en juego conocimientos anteriores para la construcción de nuevos conceptos, aplicaciones para facilitar la fijación y la generalización de conceptos y una serie de preguntas que permiten llevar un hilo conductor.
Es necesaria una formación sólida sobre el contenido matemático del concepto, lo que permite entender el sentido de cada una de las actividades que se han propuesto e identificar qué se logra con cada una de ellas, y cómo la resolución de problemas finalmente permite al estudiante la formación de conceptos por aproximaciones sucesivas (Villarraga, 2016).
Luego de llevar a cabo el desarrollo de las actividades, se arrojaron elementos que permiten determinar situaciones sobre los procesos de asimilación del concepto de función de variable compleja a través de la puesta en escena de la estrategia metodológica. En este proceso se identificó en los alumnos los siguientes resultados: los procesos de motivación son esenciales cuando se abarcan temas relacionados con la matemática, la incorporación de una vía mixta permite al docente tener diferentes perspectivas frente a cómo abarcar el contenido, el uso de situaciones problema ayuda a los estudiantes a una mejor comprensión de los conceptos, aproximadamente un 70% alcanzó un nivel óptimo frente a la comprensión no solo del concepto de función de variable compleja, sino de los conceptos asociados a este. También, se precisa que la evaluación frente al concepto de número complejo, representación y función de variable compleja se puede apreciar a medida que las actividades abarcan problemas de mayor complejidad.
El empleo de las TICs en la formación de conceptos y en especial en los procesos de enseñanza-aprendizaje en el nivel universitario, ofrece múltiples ventajas en el mejoramiento de los diferentes procesos de asimilación de conceptos, procedimientos que se tratan en el proceso de enseñanza-aprendizaje de las matemáticas, debido a que permiten la visualización y por ende la asimilación de conceptos abstractos sobre la base de imágenes o representaciones que las TICs proporcionan.
Afanasiev, V. (1979). El Enfoque sistémico Aplicado al Conocimiento social. Ciencias Sociales, 35 (1), 31-47.
Aníbal Mendoza, A., Acevedo, D. y Tejada, C. (2016). Teoría de la Formación por Etapas de las Acciones Mentales (TFEAM) en la Enseñanza y Aprendizaje del Concepto de Valencia Química, Formación Universitaria, 9(1), 71-76
Arcavi, A. (2003). The role of visual representations in the learning of mathematics. Educational Studies in Mathematics, 52(3), 215-241.
Ballester, S. et al. (1992). Metodología de la enseñanza de la matemática. Tomo I y II. La Habana: Pueblo y educación.
Campistrous, L. y C. Rizo. (1996). Aprende a resolver problemas aritméticos. Proyecto TEDI. La Habana: Pueblo y Educación.
D’Amore B. (2001). Una contribución al debate sobre conceptos y objetos matemáticos. Revista Uno. [Barcelona, España]. 27, 51-76. Recuperado de http://www.dm.unibo.it/rsddm/it/articoli/damore/402%20contribucion%20al%20debate%20sobre%20conceptos%20y%20objetos.pdf
Delors, J., Amagi, I., Carneiro, R., Chung, F., Geremek, B., Gorham, W. y Nanzhao, Z. (1997). La educación encierra un tesoro: informe para la UNESCO de la Comisión Internacional sobre la Educación para el Siglo Veintiuno. Unesco.
Duke, B. J., Dwyer, J. F., Wilhelm, J., y Moskal, B. (2008). Complex variables in junior high school: the role and potential impact of an outreach mathematician. Teaching Mathematics and its Applications, 27(1), 38-47.
Duval, R. (1999). Semiosis y pensamiento humano. Registros semióticos y aprendizajes.
Estándares Básicos de Competencias en Matemáticas. Potenciar el pensamiento matemático: ¡un reto escolar! (2006). Recuperado de http://www.mineducacion.gov.co/1621/articles-116042_archivo_pdf2.pdf p.57
Falk, M. (1980). La enseñanza a través de problemas. Bogotá: Universidad Antonio Nariño.
Falk, M. (2001). Olimpiadas de Matemáticas: retos, logros (y frustraciones). Boletín de la Asociación Matemática Vanezolana, VIII (1).
Falk, M. (2015). Mathematics and Cognition. Seminario Pensamiento Matemática y Educación Matemática. Universidad Antonio Nariño. 28 de marzo de 2015.
Fischbein, E. (1990). Introdution (Mathematics and Cognition). En: P. Neshery J. Kilpatrick (Eds), Mathematics and cognition. Cambridge: Cambridge University Press.
Galperin, G. I. (1956). Ration of the intensity components of the sodium yellow doublet in the twilight spectrum. Astron Reports, 33, 173-181.
https://doi.org/10.1007/978-94-007-0014-7
Leontiev, A. N. (1983). Teoría psicológica de la actividad. Selección de Obras de Psicología, 2, 94-261
Pérez, F. (2004). Olimpiadas Colombianas de Matemáticas para primaria 2000 - 2004. Bogotá: Universidad Antonio Nariño.
Polya, G. (1965). Cómo plantear y resolver problemas. Ciudad México: Editorial Trillas.
Prior, J. y Torregrosa, G. (2013). Razonamiento configural y procedimientos de verificación en contexto geométrico. Revista Latinoamericana de Investigación en Matemática Educativa (RELIME), 16(3), 339-368.
Ramírez Uclés, R., Flores Martínez, P., (2017). Habilidades de visualización de estudiantes con talento matemático: comparativa entre los test psicométricos y las habilidades de visualización manifestadas en tareas geométricas. Enseñanza de las Ciencias, 35.2, pp. 179-196
Rivera, F. D. (2011). Towards a visually-oriented school mathematics curriculum. Nueva York: Springer.
Rojas, O. (2009). Modelo didáctico para favorecer la enseñanza - aprendizaje de la geometría con un enfoque desarrollador. (tesis doctoral). Holguín: Universidad de Ciencias Pedagógicas José de la Luz y Caballero.
Santiesteban, I. y Rodríguez, M. (2004). Propuesta metodológica para aprender a resolver problemas matemáticos. Acta Latinoamericana de Matemática Educativa, Volumen 17.
Santos, L. (2007). La resolución de problemas matemáticos fundamentos cognitivos. México: Trillas.
Schoenfeld, A. (1985). Mathematical Problems Solving. Academic Press.
Schoenfeld, A. (1987). A brief and biased history of problem solving. In: F. R. Curcio (Ed.) Teaching and Learning: A problem Solving Focus (pp. 27–46). Reston, VA: NCTM.
Schoenfeld, A. (1994). Reflections on doing and teaching mathematics. Mathematical thinking and problem solving, 53-70.
Sfard, A. (1991). On the dual nature of mathematical conceptions: Reflections on processes and objects as different sides of the same coin. Educational studies in mathematics, 22(1), 1-36.
Sigarreta, J. M., Rodríguez, J. M., y Ruesga, P. (2006). La resolución de problemas: una visión histórico-didáctica. Boletín de la Asociación Matemática Venezolana, 13(1), 53.
Sriraman, B. y Engish, L. (2010). Theories of Mathematics Education. New York: Springer.
Tall, D., & Vinner, S. (1981). Concept image and concept definition in mathematics with particular reference to limits and continuity. Educational studies in mathematics, 12(2), 151-169.
Torregrosa, G., Quesada, H. y Penalva, M. (2010). Razonamiento configural como coordinación de procesos de visualización. Enseñanza de las Ciencias, 30(2), 327-340.
Vigotsky, L. (1988). El desarrollo de los procesos psicológicos superiores. México: Grijalbo.
Villarraga, B. (2016). Modelo didáctico para la formación del concepto de función de variable compleja mediante la resolución de problemas. (tesis doctoral no publicada). Bogotá: Universidad Antonio Nariño.
Cai, J., & Nie, B. (2007). Problem solving in Chinese mathematics education: Research and practice. ZDM, 39(5-6), 459-473.
Parra, Y., & Breda, A. (2017). La Enseñanza de o desde la Resolución de Problemas Matemáticos: concepciones de Profesores de Matemática en Formación. Acta Scientiae, 19(2).
Pochulu, M. y Rodríguez, M. (2012). Educación Matemática. Aportes a la formación docente desde distintos enfoques teóricos. Buenos Aires. Argentina.
1. Docente del programa de Licenciatura en Matemática. Universidad de los Llanos, Villavicencio, Colombia. E-mail: beatrizave@gmail.com
2. Docente del programa de Maestría y Doctorado de Educación Matemática. Universidad Antonio Nariño (UAN), Bogotá, Colombia. E-mail: orojasv69@uan.edu.co
3. Profesor Investigador de la Facultad de Matemáticas (Sede Acapulco). Universidad Autónoma de Guerrero, Acapulco, México. E-mail: josemariasigarretaalmira@hotmail.com
[Índice]
revistaespacios.com

Esta obra está bajo una licencia de Creative Commons
Reconocimiento-NoComercial 4.0 Internacional