

Vol. 41 (Nº 03) Año 2020. Pág. 30
LONDOÑO Roman, Milton A. 1; OREJUELA Cabrera, Juan P. 3 y GIL Gonzalez, Cristiam A.
Recibido: 05/11/2019 • Aprobado: 14/01/2020 • Publicado 06/02/2020
RESUMEN: Se presenta una propuesta metodológica para la programación multi-objetivo de cirugías electivas con restricciones de capacidad, la cual: maximiza el número de pacientes atendidos, minimiza el tiempo promedio de espera de los pacientes y el porcentaje medio del tiempo de cirugía no programado para los médicos. La propuesta considera pacientes con diferentes niveles de prioridad, incluyendo aquellos con fechas vencidas en sus cirugías. Para la generación de la frontera de Pareto se emplea épsilon restricciones y para la selección de una solución de la frontera para implementar, se propone una medida de desempeño basada en el balance de tiempo en función de los objetivos propuestos. Con la propuesta se obtuvieron 1875 soluciones y de las cuales 12 forman la frontera de Pareto. |
ABSTRACT: A multi-objective mathematical model with capacity constraints for scheduling elective surgeries is presented: maximizing the number of patients attended, minimizing the average waiting time of patients and the average percentage of unscheduled surgery time for doctors. For the generation of the Pareto border, epsilon restrictions are used and for the selection of a border solution to implement, a performance measure based on the time balance based on the stated objectives is proposed. 1875 solutions were obtained of which 12 form the Pareto border. |
Las cirugías se clasifican en dos tipos de casos (Pham & Klinkert, 2008): i. casos electivos, donde los pacientes generalmente pueden esperar sus operaciones; y ii. casos complementarios, que incluyen: casos de emergencia que requieren cirugía en muy poco tiempo (menos de dos horas) para evitar la pérdida de vidas o grandes daños a los pacientes, y casos urgentes que necesitan atención dentro de las 24 horas para evitar el deterioro de la salud.
La cirugía es una actividad importante para los hospitales, ya que se estima que genera alrededor de dos tercios de los ingresos hospitalarios y representa aproximadamente el 40% de los costos de recursos hospitalarios, incluidos los costos de personal e instalaciones (Conforti, Guerriero, & Guido, 2010), (Denton, Viapiano, & Vogl, 2007).
De acuerdo con (Pham & Klinkert, 2008), solo se pueden planificar y programar las cirugías electivas. La planificación determina el conjunto de cirugías que deben realizarse en un día determinado. La programación establece los tiempos de inicio y de finalización de la cirugía, y también la asignación de recursos (Salas, cirujanos, enfermeras, anestesista, etc.) (Akbarzadeh, Moslehi, Reisi-Nafchi, & Maenhout, 2019).
Una inadecuada planeación y programación de cirugías conlleva a usar horas extras de recursos limitados como las salas y los equipos médicos (Médicos, enfermeras, anestesiólogos), además implica demoras en la cirugía o cancelación de los procedimientos, que son costosos tanto para los pacientes como para el hospital (Conforti et al., 2010).
El problema de planeación y programación de cirugías implica la asignación y secuenciación, que son problemas catalogados como un NP-Hard (nondeterministic polynomial-hard) (Garey & Johnson, 1977). Dentro de las metodologías de solución se encuentra técnicas exactas (Guido & Conforti, 2017),(Molina-Pariente, Fernandez-Viagas, & Framinan, 2015),(Ribeiro, Leoneti, & Costa, 2018),(Vali-Siar, Gholami, & Ramezanian, 2018) y heurísticas (Akbarzadeh et al., 2019),(Guido & Conforti, 2017),(Molina-Pariente et al., 2015),(Duenas, Di Martinelly, Tütüncü, & Aguado, 2017),(Conforti et al., 2010),(Xiang, 2017),(Vali-Siar et al., 2018),(Meskens, Duvivier, & Hanset, 2013),(Belkhamsa, Jarboui, & Masmoudi, 2018).
La programación matemática es una de las metodologías exactas más usadas por los investigadores, sin embargo, al ser un problema NP-Hard, varios autores han implementado diferentes heurísticas y meta heurísticas de solución como: Colonia de Hormigas (Xiang, 2017), Algoritmos Genéticos (Guido & Conforti, 2017),(Vali-Siar et al., 2018),(Conforti et al., 2010), Búsqueda Local (Duenas et al., 2017),(Meskens et al., 2013) y Algoritmos Constructivos (Molina-Pariente et al., 2015), (Vali-Siar et al., 2018).
Otro aspecto importante en la programación de cirugías es que este problema participa diferentes actores, con diferentes motivaciones, lo cual genera conflictos de interés al materializarse sus respectivas funciones de desempeño que representan sus preferencias. Por ejemplo, un administrador del hospital podría estar interesado en lograr altos niveles de utilización y bajos costos, mientras que el personal médico podría preocuparse menos por los factores de costo y más bien tratar de lograr bajas horas extras o lograr un mejor bienestar para el personal médico. Al paciente, como cliente del hospital, puede importarle poco los factores anteriores y solo desea tiempos de espera cortos (Samudra et al., 2016).
Lo anterior evidencia la naturaleza multi objetivo del problema, es por ello que en la literatura se han investigado diferentes medidas desempeño y se han empleado para la solución enfoques ya sea de forma mono objetivo o multi objetivo. Dentro de las investigaciones que han empleado un enfoque mono objetivo se tienen como medidas de desempeño la utilización eficiente de los recursos: minimización de la sobre-utilización (horas extras) (Vali-Siar et al., 2018), maximización de los pacientes programados (Molina-Pariente et al., 2015); minimización de los tiempos de espera, reduciendo la tardanza de las cirugías (Molina-Pariente et al., 2015), (Vali-Siar et al., 2018), o el tiempo indirecto (Akbarzadeh et al., 2019);
De los artículos que consideraran el enfoque multi objetivo, se contemplan las siguientes funciones de desempeño, la reducción de los tiempos de espera (Xiang, 2017), (Meskens et al., 2013), el costo de los recursos (Duenas et al., 2017), y la nivelación de los recursos (Vali-Siar et al., 2018). (Guido & Conforti, 2017) Propone un modelo para maximizar el número de pacientes programados, maximizar la prioridad de los pacientes, maximizar la utilización de los quirófanos y minimizar el uso de horas extras de los recursos.
A pesar de la naturaleza multi objetivo del problema de programación de cirugías, el enfoque mono objetivo es el más empleado (Vali-Siar et al., 2018) , (Molina-Pariente et al., 2015), (Molina-Pariente et al., 2015), (Vali-Siar et al., 2018), (Akbarzadeh et al., 2019), este enfoque no permite abordar el conflicto que existe entre algunas medidas de desempeño.
Alguno autores abordan el problema considerando múltiples objetivos los consolidan a una sola función de desempeño, utilizando el método de suma ponderada, pero tal como lo menciona (Guido & Conforti, 2017) esta estrategia presenta una desventaja al momento de asignar coeficientes de peso a las funciones de desempeño. Sin embargo, esta dificultad es superada por la programación multi objetivo, cuando se emplean estrategias que definen una Frontera de Pareto.
Por otro lado existen otros aspectos importantes a tener en cuenta en la programación de cirugías, por ejemplo hay investigaciones donde se tienen en cuenta las preferencias del paciente o del cirujano, como la preferencia por practicar la cirugía en determinada sala y horario (Ribeiro et al., 2018), preferencia para realizar la cirugía con un equipo médico que tenga alta afinidad (Meskens et al., 2013).
Otro aspecto de gran importancia en este problema es la estrategia de priorización de los pacientes (Wolff, Durán, & Rey, 2012). En este sub problema se debe establecer un tiempo máximo de espera para la realización de cada cirugía, basándose en el diagnóstico y en los agravantes médicos del paciente, (Wolff, Durán, & Rey, 2012) desarrollan una estrategia de priorización basada en tres criterios que son el progreso en la enfermedad, el dolor y la discapacidad (ver figura 1).
Figura 1
Categorización del Paciente

Fuente: (Wolff, Durán, & Rey, 2012)
El presente documento aborda el problema de la programación de cirugías, bajo un enfoque multi objetivo, en que además de considerar la estrategia de priorización de (Wolff, Durán, & Rey, 2012), se considera una lista de pacientes cuyas prioridades o fechas de cirugía ya han sido vencidas.
Las medidas de desempeño, que se emplean permiten maximizar el nivel de servicio y la utilización eficiente de los recursos que intervienen en la prestación de estos servicios. Por el lado del nivel del servicio se tuvo en cuenta la minimización del tiempo de espera y la minimización del número de pacientes no atendidos; y por el lado de la utilización eficiente de los recursos se planteó, la minimización del tiempo medio no operativo de los médicos.
De acuerdo con la revisión de artículos, la minimización de la tardanza es una de las medidas de desempeño más utilizadas, sin embargo, muy pocas veces se tiene en cuenta cirugías vencidas, es decir que no fueron programadas en horizontes de programación pasados, en tal sentido en el presente artículo se tienen en cuenta estas cirugías asignándoles una fecha máxima de cirugía con valor negativo, permitiendo que el modelo programe estas cirugías en el momento más temprano posible cuando se minimice la tardanza.
La minimización del tiempo medio no operativo de los médicos no se ha considerado en la literatura, y es otro aporte en esta investigación. Esta medida de desempeño busca garantizar que los médicos con cirugías muy especializadas, poco frecuentes, se programen con una mayor prioridad, lo que es equivalente a y minimizar su tiempo no operativo.
La metodología se basa en 5 fases para la programación de cirugías electivas: Fase I, formulación del modelo matemático. Fase II: generación de soluciones. Fase III, construcción de la frontera de Pareto. Fase IV, selección de una solución final. Fase V, se realiza un análisis de correlación de los objetivos de las soluciones dominantes encontradas.

Se describe el modelo matemático para la programación de cirugías no prioritarias. Se busca establecer una programación que minimice el tiempo promedio de espera de los pacientes y que a su vez maximice el número de pacientes atendidos, considerando que existen pacientes con diferentes niveles de prioridad para su cirugía, en especial existen pacientes cuya fecha de cirugía planeada ya se encuentra vencida, dadas las limitaciones de capacidad del sistema, y que a la vez minimice el tiempo medio no operativo de los médicos.
Para este entorno, la maximización del número de pacientes atendidos, representa una medida de desempeño de interés dado que las limitantes de capacidad y la duración de las cirugías es condicional en este problema, sin embargó, esto puede ocasionar que pacientes con muy alta prioridad y con tiempos de cirugía muy altos tienda a no ser atendidos.
Por su parte la minimización de la tardanza total, puede generar que los pacientes con prioridad alta y con tiempos de cirugía muy largos se programen primero y esto podría hacerse a costa de que muchos otros pacientes no se programen, en tal sentido es necesario encontrar un equilibrio entre la espera promedio de los pacientes y número de pacientes
En cuanto a la función de desempeño de minimizar el promedio de tiempo no operativo de los médicos que, en condiciones de déficit de capacidad, se intentarán que los médicos con pocas cirugías sean programados con mayor prioridad y esto se debe balancear con la potencial tardanza que genera esto en los pacientes que pertenecen a médicos que tienen un gran número de cirugías.
Según complejidad de la enfermedad del paciente, se tiene una fecha máxima en la que la cirugía podría realizarse sin generar un compromiso mayor (Ver Figura 1).
Para cada paciente ya se sabe que medico realizará la cirugía
Los quirófanos son multifuncionales.
Los tiempos de limpieza de los quirófanos depende de la cirugía que se realice.
Todo medico después de realizar una cirugía debe tomar un receso y se asume que lo más corto que este puede ser es igual al tiempo que se realiza la limpieza del quirófano.
Las cirugías que se programen en el horizonte de planeación, solo se pueden realizar en un único quirófano sin interrupción



2.1.5.1. Minimizar el número de pacientes no atendidos
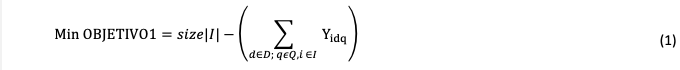
2.1.5.2. Minimizar la suma de todas las tardanzas
Minimiza las tardanzas y para esto se suma la tardanza de los pacientes que fueron programados y la tardanza de los pacientes que no fueron programados en el horizonte de programación.
La tardanza de los pacientes programados se calcula realizando la diferencia entre el día d que fue programado el paciente i y su máxima fecha para realizarle la cirugía, y solo toma valores cuando esta cirugía se programa después de la máxima fecha de entrega.
La tardanza de los no programados, asume que las cirugías que no se programan en este periodo serán programadas la semana siguiente y tiene una penalidad de 5 días debido a: que como media se atenderán estas cirugías a mitad de la semana (en el día 3, miércoles) más dos días del fin de semana.

2.1.5.3. Minimizar el porcentaje medio no operativo de los médicos
Minimizar el porcentaje medio no operativo se calcula, restándole al total de médicos que deberían ser programados la cantidad porcentual de los que fueron programados, este a su vez se determina a partir del tiempo de las cirugías que se programaron de cada médico dividido el tiempo que se requiere para realizar todas las cirugías del médico. Y para expresarlo como un promedio se divide entre el total de médicos.


Para dar solución a los modelos matemáticos multi-objetivo existe una metodología propuesta por (YV, Lasdon, & DA, 1971),se trata de épsilon – restricciones. Esta técnica, básicamente, consiste en convertir un modelo multi-objetivo en mono-objetivo, escogiendo una función objetivo como principal y configurando las demás como restricciones, asociadas a un conjunto de parámetros llamados épsilon, determinados especialmente para cada función objetivo presentada como restricción (Osorio Muriel, Brailsford, & Smith, 2014).
Inicialmente se optimiza el modelo por cada función objetivo.
Después de haber calculado las medidas de desempeño por cada función objetivo se determinan los máximos y mínimos, para calcular un rango.
Luego este rango lo dividimos por un número de pasos (np) para así obtener diferentes soluciones.
Seguidamente para los objetivos diferentes al que se va a optimizar, se calcula un límite superior que disminuye según la amplitud calculada anteriormente.
Estos límites superiores se imponen al modelo como restricciones y se optimiza el modelo.
Se obtienen las soluciones y se guardan los valores de las medidas de desempeño.
Figura 2
Algoritmo para generar soluciones con épsilon restricciones

Fuente: Autores
En problemas de optimización con un solo objetivo, el determinar si una solución es mejor que otra es fácil de resolver, solo comparamos el valor de la función objetivo en ambas soluciones. En problemas de optimización multi-objetivo, que tan buena es una solución es determinada mediante el concepto de dominancia (Villarreal Marroquín, 2015). Donde estas soluciones dominantes conforman la frontera de Pareto.
Dadas 2 soluciones x1 y x2, se dice que x1 domina a x2, si (Villarreal Marroquín, 2015):
En otras palabras, cada solución i está compuesta por un conjunto de características que componen un estado, en la literatura una combinación de valores de cada una de las características de un estado se denomina label o etiqueta. Sea Li el label de la solución i, compuesta por cada uno de los valores de las funciones objetivo alcanzadas por tal solución: Li= (OBJETIVO1i OBJETIVO 2i, OBJETIVO 3i).
Sean L1 y L2, las etiquetas de dos soluciones cualquiera. L1 dominará al label L2 si OBJETIVO11<= OBJETIVO12, OBJETIVO21<= OBJETIVO22, OBJETIVO31<= OBJETIVO32. Esto significa que el label L1 supera o iguala en todas las características del label L2. L1 dominará fuertemente L2 si todas sus características son superadas. Un label dominado supedita a que su respectiva solución sea eliminada del conjunto de soluciones, debido a que existe una o más soluciones dominantes que encuentran soluciones de mejor calidad. Cuando del conjunto de soluciones no puede eliminarse más elementos porque no existen más label dominados, este conjunto se denomina en este trabajo como soluciones dominantes o frente de Pareto.
Todos los puntos de la frontera de Pareto no dominados son eficientes en las medidas de desempeño, sin embargo, ello no resuelve el problema de establecer que solución implementar que es lo que requiere la entidad objeto de estudio. Y para la elección de una solución final respecto a las dominantes, se propone el indicador PAC/MED; esta expresión computa las horas de cirugía de los pacientes que no fueron programados en la solución respecto al número equivalente de médicos ocupados.
El porcentaje de no ocupación de una solución (OBJ3) es una representación de la proporción media de la carga de trabajo de cada médico (en termino de tiempo) que no es atendida, haciendo que el modelo matemático tenga mayor predilección por no satisfacer pacientes con cirugías que requieren menor tiempo, y que pertenecen a aquellos médicos con mayor número de horas de cirugías a programas dado las restricciones de capacidad, ya que estos pacientes ponderan porcentualmente menos que un paciente de un médico con pocas horas a programar en su carga laboral.
Esto tiene dos efectos indirectos deseables para la operación de las salas de cirugía. Por un lado, propende a mantener programadas cirugías de médicos con menor carga procurando que todos los médicos tengan pacientes programados cada semana, su relación con el hospital se mantenga y la reputación del servicio por tener menor frecuencia de operación no se vea afectada con sus pacientes.
Por otro lado, pacientes con cirugías que requieren menor tiempo, tienen mayor probabilidad de agendamiento a posteriori de la programación, debido a cancelaciones de cirugías de tiempos igual o mayor a los requeridos, y dada su urgencia, podrían ser realizadas no por los médicos originalmente destinados, sino por aquellos con disponibilidad de tiempo, haciendo que los niveles de servicio incrementen con mayor facilidad. (obteniéndose así, un incremento en los niveles de servicio.)
Con el fin de identificar la relación entre las funciones objetivo se realiza un análisis estadístico de las soluciones que finalmente fueron las dominantes. Para este análisis se utilizó el Coeficiente de Correlación Spearson. Este, tiene por objetivo medir la fuerza o grado de asociación entre dos variables aleatorias cuantitativas que poseen una distribución normal bivariada conjunta. (Restrepo & Gonzáles, 2007)
La propuesta se valido en una clínica del Centro del Valle del Cauca, Colombia, la cual presta servicios de salud altamente especializados, a esta llegan pacientes remitidos de los hospitales regionales de algunos municipios del centro y norte del departamento del Valle del Cauca como Tuluá, Andalucía, Bugalagrande, Riofrío, Trujillo, San Pedro, Roldanillo, El Dovio, Bolívar, Sevilla y Caicedonia. La clínica cuenta con un gran número de especialistas: cardiólogos, dermatólogos, siquiatras, neurólogos y nefrólogos, entre otros. Además cuentan con unidades especiales, tales como neurocirugía, unidad renal, unidad de cuidados intensivos, laboratorios especializados, imágenes como TAC y resonancia magnética entre otros.
El modelo de optimización fue implementado en AMPL y el MILP fue solucionado con CPLEX 12.4, buscando satisfacer las necesidades de 77 pacientes (p), los cuales demandan cirugías que consumen tiempos de sala entre 30 y 210 minutos. Cada uno de estos pacientes, tiene una fecha postergada (vencida) si su cirugía no fue programada en horizonte de programación pasada, o con una fecha de expectativa de cirugía a lo largo de los 5 días calendario de la semana (d) y asignado a uno de los 26 médicos disponibles (m), para cada paciente se debe definir si él es operado o no, y en cuál de las 4 salas multifuncionales (q) y en qué día de la semana.
El modelo matemático se ejecutó en el software de modelación matemática AMPL (A Mathematical Programming Language) en un computador con procesador AMD Ryzen de 3.6GHz y una memoria RAM de 32 GB (Gigabyte).
El modelo inicialmente se ejecutó 3 veces de forma mono-objetivo, y en cada ejecución varió solo la función objetivo, este modelo presentó 142 variables continuas y 1528 enteras binarias, arrojando los resultados que se presenta en la tabla 1.
Tabla 1
Resultados por ejecución y
por medida de desempeño.
Número de Pacientes no atendidos |
Tardanza total en días |
% No operativo de los médicos |
|
Ejecución 1 |
8 |
139 |
14.86 |
Ejecución 2 |
8 |
85 |
16.83 |
Ejecución 3 |
12 |
164 |
7.92 |
Fuente: Autores
Con los valores de funciones obtenidas, se definieron los máximos, mínimos y rangos de cada objetivo, ver tabla 2. Dado que son 26 médicos y que el objetivo tres tiene como mayor valor este número de médicos, se empleó 25 como el número de paso para cada objetivo, con esto el modelo se ejecutó 1875 veces en AMPL, por cada uno de los tres objetivos 125 que son los 25X25 paso de los otros dos objetivos.
Derivado de la metodología para determinar la frontera de Pareto mediante la tupla de las tres funciones objetivo-deseadas: pacientes no atendidos (OBJ1), tardanza total (OBJ2) y no ocupación de médicos (OBJ3). En general, entre 8 y 12 fue el número de pacientes no atendidos; la tardanza total (días de desvió respecto a la fecha esperada de cirugía por el paciente) entrego cifras entre 85 y 164 días; y la no ocupación de los médicos se registró entre 7.92 % y 16.6% del tiempo requerido para cirugías, ver tabla 2.
Tabla 2
Valores para obtener épsilon restricciones
Min |
Max |
Rango |
Número Pasos |
Amplitud |
|
Objetivo 1 |
8 |
12 |
4 |
25 |
0.16 |
Objetivo 2 |
85 |
164 |
79 |
25 |
3.16 |
Objetivo 3 |
7.92 |
16.6 |
6.9 |
25 |
0.356 |
Fuente: Autores
Con las 1875 soluciones y los valores de cada una de las tres funciones de desempeño, se aplica un algoritmo “Non-dominated Sorting”, el cual se implementó y se ejecutó en el Software de programación MATLAB, y así seleccionar las soluciones no dominadas y construir la frontera de Pareto, ver gráfica 1. Como resultado se identificaron 12 soluciones no dominadas que hacen parte de la frontera de Pareto estas se resaltan en color naranja en la gráfica 1.
Gráfica 1
Grafica de soluciones
con su frontera de Pareto.

Fuente: Autores
En la tabla 3, se tabulan los valores numéricos para las múltiples funciones objetivo valoradas en el modelo para los 12 puntos dominantes, también se incluye el valor del indicador PAC/MED.
De las soluciones dominantes, fue elegida la solución número 5 por su indicador PAC/MED de 0.5089, el menor valor de todos. Esta solución tiene la particularidad que atiende el mayor número de cirugías posibles, a pesar de que entre el conjunto de soluciones con esta misma característica es la de peor tardanza total, tiene una diferencia de 5 días respecto a la mejor tardanza total encontrada.
La ventaja de esta solución radica en su porcentaje de no ocupación (9,31%), el cual es el menor posible entre todas las soluciones con 8 pacientes no atendidos (con 12 horas de cirugías pendientes a ser programadas) y equivale proporcionalmente al tiempo de 2,42 médicos disponibles. Por lo tanto, el indicador PAC/MED para la solución número 5 es interpretado como: potencialmente cada uno de estos médicos disponibles equivalentes en promedio pueden realizar 0.5089 horas de cirugía de pacientes no programados por el sistema, quedando la programación de cirugías como se detalla en la tabla 4.
Tabla 3
Soluciones dominantes
NO ATENDIDOS |
TARDANZA TOTAL |
NO OCUPACIÓN |
PAC/MED |
|
1 |
8 |
85 |
11.58% |
0.5220 |
2 |
8 |
86 |
10.53% |
0.5159 |
3 |
8 |
87 |
10.16% |
0.5137 |
4 |
8 |
88 |
9.69% |
0.5111 |
5 |
8 |
90 |
9.31% |
0.5089 |
6 |
9 |
94 |
9.02% |
0.5707 |
7 |
9 |
94 |
8.90% |
0.5700 |
8 |
9 |
96 |
8.43% |
0.5670 |
9 |
9 |
98 |
8.18% |
0.5655 |
10 |
10 |
103 |
8.12% |
0.6279 |
11 |
11 |
110 |
7.97% |
0.6896 |
12 |
12 |
116 |
7.92% |
0.7518 |
Fuente: Autores
Una solución es dominante cuando no existe otra solución que pueda mejorar o igualar el desempeño de la solución en las tres funciones objetivo formuladas. Como datos particulares se encontró que:
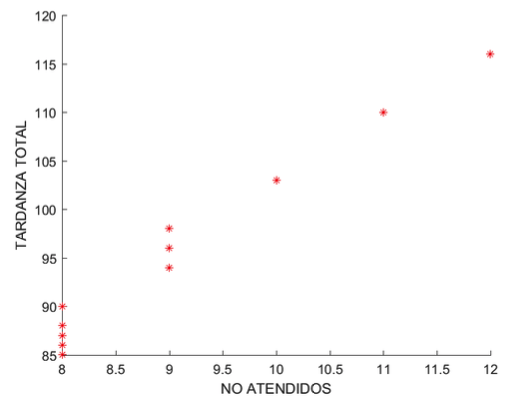
Existe una correlación (de Spearson) fuerte entre las funciones OBJ1 y OBJ2: r2 igual a 0.986 (Gráfica2). En otras palabras, a menor número de pacientes atendidos mayor retraso en el día de operación. Resultado no tan intuitivo, porque ante la posibilidad de atender un número menor de cirugías, la capacidad adicional podría favorecer los pacientes con diferencias en sus fechas esperadas (tardanza total). Para atender un número menor de pacientes obligatoriamente, el modelo debe retirar de la programación de pacientes con un consumo de tiempo menor e incluir pacientes de mayor consumo de tiempo de cirugía, pero dado la naturaleza entera del modelo, esto obliga a generar nuevas combinaciones de operaciones entre días y eventualmente entre días, desmejorando el OBJ2.
Gráfica 2
No Atendidos VS
Tardanza total
Fuente: Autores
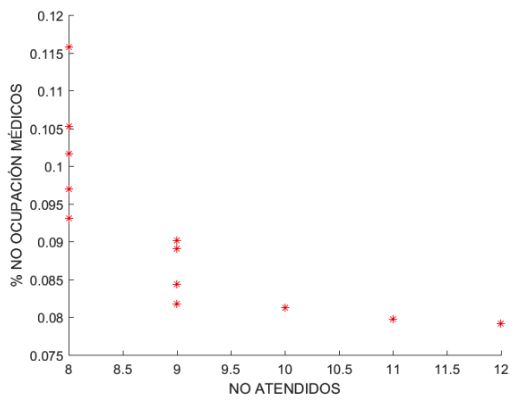
Existe una correlación (de Spearson) fuerte entre las funciones OBJ2 y OBJ3 (Gráfica 3): r2 igual a -0.839. En otras palabras, a mayor retraso en el día de operación mayor no ocupación de los médicos. Si observamos este resultado, desde la perspectiva de OBJ1 vs OBJ3 (Gráfica 4) (r2 = -0.757) significa que para atender un número mayor de pacientes el modelo debe cambiar en la programación pacientes de consumo de mayor tiempo por pacientes de menor consumo de tiempo, haciendo que algún medico se ocupe menos y por ello deteriorando OBJ3. Esto es consecuente con la conclusión derivada entre la correlación de OBJ1 vs OBJ2.
Gráfica 3
No atendidos VS
% No ocupación médicos
Fuente: Autores
-----
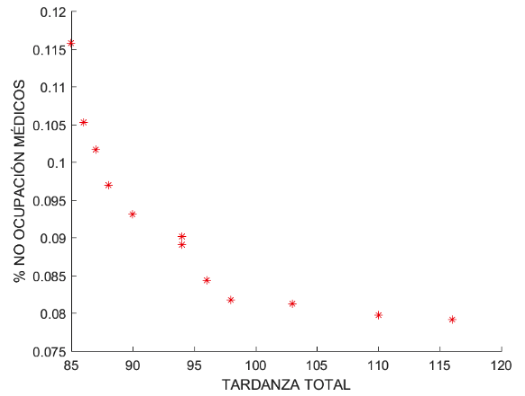
Gráfica 4
Tardanza total VS
% No ocupación médicos
Fuente: Autores
A continuación, en la tabla 4, se presenta una propuesta de programación de los quirófanos derivada de la solución que se seleccionó mediante el indicador PAC/MED, que este caso fue la solución 5. Dado que el modelo asigna en el mismo quirófano las cirugías que se realizan por el mismo médico, y además controla la capacidad de los quirófanos y los médicos por día, para obtener una programación detallada se pueden emplear simples reglas de despacho o algunos criterios adicionales, en este caso se programa las cirugías del mismo medio consecutivas y se emplea la regla SPT (Shortest Processing Time), donde las cirugías con menor duración se programan de primero.
Tabla 4
Programación de
cirugías propuesta

Fuente: Autores
En esta investigación se ha propuesto un modelo de programación de cirugías multi-objetivo que considera niveles de prioridad de los pacientes basado en la complejidad de sus procedimientos. Además, resaltar que esta metodología considerando múltiples objetivos permitió brindar una solución que mejora el nivel del servicio y la utilización eficiente de los recursos. La instancia de aplicación del modelo es derivada de la realidad de un hospital colombiano con prestación de servicios nivel III. Los resultados son prometedores, mostrando las ventajas de realizar herramientas de programación, en este caso, para salas de cirugías electivas.
De acuerdo con el estado del arte, diferentes investigaciones han abordado el problema de asignación y programación con medidas de desempeño como la minimización de la tardanza y la minimización de pacientes no atendidos, sin embargo, la función de desempeño que busca minimizar el tiempo no operativo de los médicos no se ha tenido en cuenta, y es una medida que aporta en gran medida la programación de cirugías electivas ya que permite maximizar el número de pacientes atendidos por un médico.
Además, cuando se tienen cirugías atrasadas y se sabe que por problemas de capacidad no todas las cirugías pueden ser programadas, minimizar esta medida de desempeño (tardanza y pacientes no atendidos) sin imponer restricciones de cumplimiento de demanda genera infactibilidad técnica en el caso real.
Otro aspecto relevante de la investigación es la programación de pacientes de acuerdo a su priorización, según la metodología planteada, los pacientes con fechas vencidas y prontas a vencerse son programados lo más temprano posible, cuando se minimiza la tardanza, mejorando por ende el nivel de servicio y la satisfacción de estos.
Investigaciones futuras se centrarán en dos ramas: primero, existen variantes como la asignación de médico a cirugía/paciente, salas de cirugías dedicadas y de capacidades heterogéneas entre otras restricciones de paciente que enriquecen el problema desde la perspectiva del entorno de la salud colombiana y las especificidades del caso en el que se aplique. Segundo, desde la formulación y el desempeño del modelo, aún con resultados prometedores, la naturaleza entera de este problema (que se aproxima a un set covering problem) requiere ser abordado desde técnicas más avanzadas de solución que puedan garantizar soluciones cercanas a las óptimas ya sean desde métodos heurísticos, meta-heurísticos o exactos a instancias más grandes o complejas (como por ejemplo incluir la decisión de asignación de médico a paciente/cirugía).
La modelación propuesta esencialmente explota la no dependencia de los tiempos de cirugía ni por trabajos sucesivos. Se proponen restricciones que controlan el uso de una sala de cirugía para un mismo médico en un mismo día solo haciendo uso de las variables de asignación Yidq, evitando la creación de un conjunto de variables binarias adicionales que prolongan los tiempos de solución, estas simplificaciones no son normalmente abordadas en problemas de programación generalmente por la complejidad de creación de estas restricciones y/o por el acotamiento sub-óptimo del espacio solución. Lo que en nuestro caso no sucede por la estructura del problema real que abordamos.
Akbarzadeh, B., Moslehi, G., Reisi-Nafchi, M., & Maenhout, B. (2019). The re-planning and scheduling of surgical cases in the operating room department after block release time with resource rescheduling. European Journal of Operational Research, 278(2), 596–614. https://doi.org/10.1016/j.ejor.2019.04.037
Belkhamsa, M., Jarboui, B., & Masmoudi, M. (2018). Two metaheuristics for solving no-wait operating room surgery scheduling problem under various resource constraints. Computers and Industrial Engineering, 126(July), 494–506. https://doi.org/10.1016/j.cie.2018.10.017
Conforti, D., Guerriero, F., & Guido, R. (2010). A multi-objective block scheduling model for the management of surgical operating rooms: New solution approaches via genetic algorithms. 2010 IEEE Workshop on Health Care Management, WHCM 2010, 1–5. https://doi.org/10.1109/WHCM.2010.5441264
Denton, B., Viapiano, J., & Vogl, A. (2007). Optimization of surgery sequencing and scheduling decisions under uncertainty. Health Care Management Science, 10(1), 13–24. https://doi.org/10.1007/s10729-006-9005-4
Duenas, A., Di Martinelly, C., Tütüncü, G. Y., & Aguado, J. (2017). A multi-objective hospital operating room planning and scheduling problem using compromise programming. Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 10061 LNAI, 379–390. https://doi.org/10.1007/978-3-319-62434-1_31
Garey, M. R., & Johnson, D. S. (1977). Computers and intractability: a guide to the theory of NP-completeness, Freeman.
Guido, R., & Conforti, D. (2017). A hybrid genetic approach for solving an integrated multi-objective operating room planning and scheduling problem. Computers and Operations Research, 87, 270–282. https://doi.org/10.1016/j.cor.2016.11.009
Meskens, N., Duvivier, D., & Hanset, A. (2013). Multi-objective operating room scheduling considering desiderata of the surgical team. Decision Support Systems, 55(2), 650–659. https://doi.org/10.1016/j.dss.2012.10.019
Molina-Pariente, J. M., Fernandez-Viagas, V., & Framinan, J. M. (2015). Integrated operating room planning and scheduling problem with assistant surgeon dependent surgery durations. Computers and Industrial Engineering, 82, 8–20. https://doi.org/10.1016/j.cie.2015.01.006
Osorio Muriel, A. F., Brailsford, S., & Smith, H. (2014). Un modelo de optimización bi-objetivo para la selección de tecnología y asignación de donantes en la cadena de suministro de sangre. Revista Sistemas &Telemática, 12(30), 9–24.
Pham, D. N., & Klinkert, A. (2008). Surgical case scheduling as a generalized job shop scheduling problem. European Journal of Operational Research, 185(3), 1011–1025. https://doi.org/10.1016/j.ejor.2006.03.059
Restrepo, L., & Gonzáles, J. (2007). From Pearson to Spearman. Revista Colombiana de Ciencias Pecuarias, 20(2), 183–192. Retrieved from http://www.scielo.org.co/scielo.php?script=sci_arttext&pid=S0120-06902007000200010
Ribeiro, J. F. F., Leoneti, A. B., & Costa, A. L. (2018). A two-phase method for operating room scheduling. Brazilian Journal of Operations & Production Management, 15(4), 471–480. https://doi.org/10.14488/bjopm.2018.v15.n4.a1
Samudra, M., Van Riet, C., Demeulemeester, E., Cardoen, B., Vansteenkiste, N., & Rademakers, F. E. (2016). Scheduling operating rooms: achievements, challenges and pitfalls. Journal of Scheduling, 19(5), 493–525. https://doi.org/10.1007/s10951-016-0489-6
Vali-Siar, M. M., Gholami, S., & Ramezanian, R. (2018). Multi-period and multi-resource operating room scheduling under uncertainty: A case study. Computers and Industrial Engineering, 126(March), 549–568. https://doi.org/10.1016/j.cie.2018.10.014
Villarreal Marroquín, M. G. (2015). Optimización Multi- ‐‑ objetivo Contenido. 99. Retrieved from http://modelacion2015.eventos.cimat.mx/sites/modelacion2015/files/Maria_Guadalupe_Villarreal-Optimizacion_Multi-objetivo1.pdf
Xiang, W. (2017). A multi-objective ACO for operating room scheduling optimization. Natural Computing, 16(4), 607–617. https://doi.org/10.1007/s11047-016-9607-9
YV, Y. H., Lasdon, L. S., & DA, D. W. (1971). On a bicriterion formation of the problems of integrated system identification and system optimization. IEEE Transactions on Systems, Man and Cybernetics, 47(JULy), 296–297.
1. Ingeniero Industrial, Universidad del Valle, Cali, Colombia, Facultad de ingenierías, Escuela de ingeniería industrial. milton.londono@correounivalle.edu.co
2. Profesor Tiempo completo, Universidad del Valle, Cali, Colombia, Facultad de ingenierías, Escuela de ingeniería industrial. Master en Ingeniería industrial, Ingeniero industrial, universidad del Valle. juan.orejuela@correounivalle.edu.co
3. Ph.D (c) Sistemas de Ingeniería, Facultad de Ciencias Físicas y Exactas, Universidad de Chile, Chile. cristiam.gil@gmail.com
[Índice]
revistaespacios.com

Esta obra está bajo una licencia de Creative Commons
Reconocimiento-NoComercial 4.0 Internacional