

Vol. 41 (Nº 01) Año 2020. Pág. 7
ORAMAS, Onailis 1; ORTIZ, Maritza 2 y MARQUEZ Sánchez, Fidel 3
Recibido: 16/08/2019 • Aprobado: 28/12/2019 • Publicado 15/01/20
RESUMEN: Esta investigación hace uso de la lógica difusa para establecer la política óptima de inventarios de 10 productos seleccionados de un Centro Comercial, perteneciente a la cadena de tiendas TRD Caribe los cuales tienen una política de revisión continua y sus parámetros presentan incertidumbre en su comportamiento. El uso de la matemática de la borrosidad ofreció esencialmente, la flexibilidad de la que se encuentran desprovistos los modelos que se desarrollan en los ámbitos de la certeza y del riesgo. |
ABSTRACT: This research makes use of the fuzzy logic to establish the optimal inventory policy of 10 selected products from a shopping center, belonging to the TRD Caribe chain of stores, which have a policy of continuous review and their parameters present uncertainty in their behavior. The use of the fuzzy logic offered, essentially, the flexibility of which the models of the fields of certainty and risk are lacking. |
Integración multinacional, globalización de los mercados, crisis económico-financiera, internacionalización de las culturas, riesgo, incertidumbre alrededor del futuro, lucha por la seguridad alimentaria y por el cuidado medioambiental son, entre otros, procesos que impactan profundamente tanto a las organizaciones como al hombre en su papel de consumidor y de trabajador.
Esta realidad impone un gran reto a la logística empresarial, dada la imperiosidad de, por un lado, entregarle al cliente el producto o servicio exigido, y por otro, de concentrar esfuerzos con el fin de minimizar los costos y de desarrollar estrategias que desemboquen en una mejor posición ante la competencia.
Es en la gestión de aprovisionamiento donde primero se ha de hacer hincapié, especialmente en la administración de inventarios, pues esta constituye un área perfecta para la reducción de los costos, sin afectar, ni la calidad del bien o servicio ofertado, ni la generación de ingresos; jugando un papel primordial la utilización, para ello, de técnicas o modelos económico-matemáticos que, dada la diversidad y complejidad del entorno, necesitan ser esquemas cada vez más flexibles.
Existen diversos modelos de inventario, entre los que se destacan el modelo EOQ (cantidad económica de pedidos) que opera bajo la filosofía de punto de reorden, momento en el cual se debe hacer un pedido, dependiendo del nivel de inventario que se tenga, quiere ello decir que, bajo revisión continua, se realiza un pedido con una cantidad siempre fija, suficiente para tener los inventarios cerca del nivel deseado. Sin embargo, es bastante posible que se tenga faltante durante el plazo de entrega del pedido (Asencio Cristóbal, González Asencio E, & Lozano Robles 2017), pues dada la variabilidad de los parámetros, los pronósticos que se realizan de las demandas y/o el tiempo de entrega ofrecen soluciones con un alto grado de incertidumbre. El uso de la lógica difusa o matemática de la borrosidad para el tratamiento de la incertidumbre concede esencialmente, la flexibilidad de la que se encuentran desprovistos los modelos deterministas y probabilistas de inventario.
El presente trabajo tiene como objetivo responder una interrogante cuya solución sugiere cambios en los modelos empleados para establecer los parámetros del sistema de inventario a implementar en una organización: ¿cómo proceder a la hora de determinar la política de inventario de un producto, cuando los parámetros del mismo son inciertos?
En un conjunto clásico se asigna el valor 0 ó 1 a cada elemento para indicar la pertenencia o no a dicho conjunto. Esta función puede generalizarse de forma que los valores asignados a los elementos del conjunto caigan en un rango particular, y con ello indiquen el grado de pertenencia de los elementos al conjunto en cuestión. Esta función se denomina “función de pertenencia” y el conjunto por ella definido, “conjunto borroso”. La función de pertenencia µA por la que un conjunto borroso A se define, siendo [0, 1] el intervalo de números reales que incluye los extremos, tiene la forma:
µA=X→ [0, 1]
Un subconjunto de un conjunto no comprende la totalidad de los elementos del conjunto (conjunto referencial), aunque a veces por comodidad los matemáticos asumen que un conjunto es un subconjunto de sí mismo. Dado un conjunto borroso referencial se construyen subconjuntos borrosos de tal manera que la función característica de pertenencia µ(x) puede tomar sus valores no solo en el conjunto {0 ,1} sino en el segmento [0, 1], es decir en 0, 1 y también en todos los valores intermedios, de tal manera que se asignará un valor tanto más cercano a la unidad cuanto más se acerque o cumpla el elemento considerado la propiedad o proposición establecida. Con el fin de distinguir el subconjunto borroso del subconjunto ordinario se acostumbra a colocar una tilde (~) debajo de la letra mayúscula que lo representa (Kauffman, Aluja, & Pirla, 1986).
El gran mérito de la teoría de los subconjuntos borrosos consiste en que, a través de ella, se han podido traducir los matices en símbolos matemáticos mediante los cuales se consigue arribar a conclusiones también matizadas.
Resulta importante destacar que los subconjuntos borrosos se asocian a distribuciones de posibilidad, las cuales son diferentes de las distribuciones de probabilidad. (Bustelo de la Casa, 2018)
Se define un número borroso como un subconjunto borroso del referencial de los reales, que tiene una función de pertenencia normal (debe existir una Xi para la que μ (x) toma el valor 1) y convexa (cualquier desplazamiento a la derecha e izquierda de este valor xi,μ (x) va disminuyendo) (Kauffman, Aluja, & Pirla, 1986).
Un número borroso puede ser representado a través de los segmentos formados al “cortar” (asignar un valor) la función de pertenencia a unos determinados niveles α (nivel de presunción), como se ilustra en la siguiente figura:
Figura 1
Número Difuso Normal
y Convexo con α- cortes.
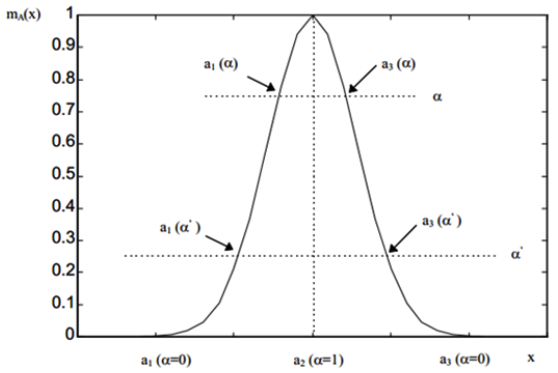
Fuente: (Morrillas Raya, 2006)
A medida que el nivel de presunción α disminuye, los segmentos obtenidos se encajan progresivamente. El nivel 0 corresponde siempre al referencial y al máximo nivel de presunción (1) es posible que el subconjunto sea vacío.
Al concepto de α-corte también se le llama conjunto de nivel (umbral) α. Este concepto permite un enfoque muy interesante de la teoría de subconjuntos borrosos, ya que la familia formada por los α-cortes contiene toda la información sobre el subconjunto borroso. Quizás el α-corte sea uno de los conceptos más importantes, dado que, ajustando el valor se determina el rango o conjunto de valores que satisfacen un determinado grado de pertenencia o compatibilidad (Gutierrez, Vergara , Rodríguez, & Baber, 2018).
Expertos plantean que la teoría de los números borrosos puede considerarse como una ampliación de la teoría de los intervalos de confianza, cuando se consideran estos intervalos a todos los niveles desde 0 hasta 1, en lugar de considerar un solo nivel (Aluja & Kaufman, 1986). Al decir de Gil Aluja y Kaufmann: “un número borroso es una secuencia finita o infinita de intervalos de confianza” (Kaufman, Aluja, & Barre, 1987)
Los intervalos de confianza son uno de los elementos principales de la matemática borrosa, dado que el intervalo de confianza recoge un rango de valores en el cual va a encontrarse el valor buscado o especificado de la variable en estudio. (Bustelo de la Casa, 2018)
De todo lo anterior se puede concluir que un número borroso se caracteriza por los pares “nivel de presunción”; “intervalo de confianza”, ya que a cada nivel de presunción le corresponde un intervalo de confianza.
De esta forma, un número borroso asocia dos conceptos: relacionado a la noción de incertidumbre se encuentra el concepto de intervalo de confianza y relacionado a la percepción del individuo el de nivel de presunción. Por analogía, el concepto de variable aleatoria está relacionado a la noción de aleatoriedad y por ley de probabilidad a la concepción de medida (Rondón Casas, Farreras Noguer, & Linares, 2015)
La particularidad del número borroso triangular consiste en estar determinado por tres cantidades: una por debajo de la cual no va a descenderse, otra a la que por encima no será posible llegar, y finalmente, aquella que representa el máximo nivel de presunción (Kauffman, Aluja, & Pirla, 1986). La representación gráfica del número borroso triangular queda reflejada en un sistema de coordenadas de la siguiente forma:
Figura 2
Número difuso triangular

Fuente: (Morrillas Raya, 2006)
Alternativamente se puede precisar un número borroso triangular definiendo el intervalo de confianza de nivel α como sigue:
Con los números borrosos triangulares se pueden realizar operaciones matemáticas tales como adiciones y sustracciones; si por el contrario se efectúan multiplicaciones y divisiones el resultado constituye una aproximación triangular, pues el número borroso obtenido ha quedado deformado, es decir las funciones de pertenencia dejan de ser lineales para ser, por ejemplo, parabólicas.
En este apartado se plantea un modelo matemático que permite representar el comportamiento de los sistemas de inventario aplicando la lógica de la borrosidad, para así determinar la política a seguir en términos de cuánto pedir y cada qué tiempo, de manera que se logre el manejo del sistema con un costo total económico; de ahí la importancia práctica del mismo para la toma de decisiones en las empresas en condiciones de incertidumbre.
Antes de plantear la formulación matemática del modelo, es necesario puntualizar algunos elementos generales relacionados con los sistemas de inventario, donde la incertidumbre juega un papel primordial, los cuales están referidos a:
Con independencia del tipo de modelo que lleve a cabo la entidad objeto de estudio para gestionar sus stocks, el propósito del diseño de las políticas de inventario es minimizar los costos totales en los que incurre la organización por ese concepto.
Existe un conjunto de costos relacionados con los sistemas de inventario y que tributan a la magnitud del costo total. Estos son:
“En la práctica, tanto el costo del lanzamiento de un producto (Co) como su costo de conservación (Ch), no se conocen con exactitud, de ahí que se pueda plantear que Co y Ch son números borrosos y que, para mayor facilidad, toman la forma triangular” (Aluja & Kaufman, 1986). Sean, pues:

La demanda (D), su comportamiento, resulta de vital importancia a la hora de determinar el modelo matemático más adecuado para la gestión de los inventarios, sobre todo aquellos artículos cuya demanda está influenciada por las condiciones del mercado y existe gran incertidumbre en cuanto a su valor real.
Los modelos se clasifican en deterministas, cuando la demanda es conocida y constante, y probabilista cuando esta es aleatoria pero su comportamiento se puede establecer a través de un patrón de probabilidad.
Para los productos con demanda independiente y aleatoria, en el procedimiento para la Gestión de Inventarios en Empresas Comerciales y de Servicios (GISERCOM) (Ortiz Torres M., 2012) se propone realizar un estudio de su comportamiento teniendo en cuenta tres escenarios posibles: pesimista, más probable y optimista, para así obtener un intervalo que encierre los valores mínimo y máximo en los que puede oscilar la demanda de ese producto.
Partiendo de dicho resultado las autoras consideran que es posible la formación de un número borroso triangular (tal como se procedió anteriormente con los costos), cuyo límite inferior equivale al valor del escenario pesimista (D1), el límite superior coincidirá con el escenario optimista (D3) y el valor central será el del escenario más probable (D2) y corresponderá al máximo nivel de presunción. (Ortiz Torres & Oramas Santos, 2015)
Alternativamente se puede definir dicho número triangular en forma de intervalo de confianza para su posterior utilización en dependencia del modelo matemático seleccionado, como sigue (Oramas Santos, 2014).
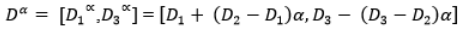
Cuando se habla de suministro se hace referencia a la cantidad y forma en que los productos se reciben en la empresa, de ahí que, en este momento, sean los proveedores los que adquieran un papel primordial, teniendo en cuenta la variedad de sus ofertas y sus condiciones.
Los atributos más importantes a tener en cuenta en este sentido serán:
En tal sentido se considerará en esta investigación la incertidumbre en el parámetro tiempo de entrega del suministrador, estableciéndose el mismo como un número borroso triangular cuyo tratamiento será exactamente el mismo que el de la demanda:

Una vez apuntados los elementos fundamentales que caracterizan los sistemas de inventario donde la incertidumbre juega un papel preponderante, se proseguirá al desarrollo del modelo de inventario EOQ básico. Dicho modelo toma por base las ecuaciones matemáticas que ya han sido definidas con anterioridad por los estudiosos del tema para los modelos deterministas de inventario; pero introduciendo las variaciones correspondientes a los parámetros demanda, tiempo de entrega del suministrador, costo de ordenar y de conservar a través de los números borrosos triangulares e intervalos de confianzas definidos con anterioridad.
En estas condiciones se consideran supuestos los siguientes:
Además, Ch se trabajará en $/u/año y el horizonte de planificación es de un año, por lo que la demanda a emplear será la anual.


La entidad objeto de estudio es un Centro Comercial perteneciente a la cadena de tiendas TRD Caribe, cuya actividad económica fundamental es la venta de productos tanto alimenticios como no alimenticios, contando con diferentes departamentos que brindan al público artículos de perfumería, equipos electrónicos y electrodomésticos, confecciones, calzado, entre otros.
La actividad comercial tiene, entre otras, las siguientes funciones:
Dado que el objetivo de la investigación se centra en el diseño de políticas de inventarios en condiciones de incertidumbre resulta necesario describir en detalle cómo se efectúa la actividad de almacenamiento en la entidad objeto de estudio.
La actividad relacionada con el almacenaje tiene entre sus funciones:
Los clientes potenciales de esta entidad son las personas residentes en el municipio donde se ubica el Centro Comercial y la población de municipios cercanos, de ahí la afluencia de gran cantidad de personas, mayormente en los meses que se conmemoran fechas significativas debido a la variedad de productos ofertados, siendo esta una oportunidad para incrementar las ventas. Además, es suministradora de mercancías de los kioscos [5] que forman parte de la propia cadena TRD cuando estos incurren en agotamiento de existencias.
Con el fin de determinar la situación de la gestión de aprovisionamiento en el centro comercial se realiza un diagnóstico de la misma, presentándose las principales dificultades:
Dado que la política de revisión de los inventarios es de forma continua, el modelo de gestión de stocks a aplicar en esta entidad se corresponde con el modelo de cantidad fija de reorden. En el caso de la presente investigación se seleccionó una muestra de 10 productos en el área de perfumería. Para ello se aplicó el método ABC multicriterio [6], escogiéndose los 10 productos de mayor puntuación.
Los números borrosos triangulares correspondiente a los parámetros del modelo: demanda anual, costo de ordenar un pedido, costo de conservación por unidad de producto y de tiempo, así como el tiempo de entrega del suministrador fueron determinado por un equipo de experto formado en su mayoría por los especialistas comerciales de la entidad.
Los resultados obtenidos para las variables Q, CT, R y T resultantes de la aplicación del Modelo EOQ en condiciones de incertidumbre desarrollado por las autoras para cada uno de los productos se presentan en la tabla que se muestra a continuación:
Tabla 1
Intervalos de Q, C, R y T.

Los resultados presentados permiten el diseño de políticas de inventario para cada uno de los productos de la muestra. Por ejemplo para el producto Jabón de tocador 125 mg M. Four Seasons (1) se deben emitir pedidos cuando los niveles de inventario alcancen entre 473 y 591 unidades, y el tamaño del lote a solicitar oscilará entre las 3462 y 4784 unidades de producto, para un tiempo de ciclo de 0.2 a 0,3 de años, es decir entre 73 y 110 días aproximadamente, superior al tiempo de entrega del suministrador como se indicó en uno de los supuestos del modelo. El costo total anual de inventario de aplicar esta política a este producto oscilará entre $143 y $285 aproximadamente. El mismo razonamiento realizado con este producto es válidos para el resto de los productos de la muestra.
Como se puede apreciar los resultados obtenidos en forma de intervalo le dan a la empresa cierta movilida en el proceso de toma de deciones con relación a la política de inventario a mantener, de forma tal que se puedan ir ajustando en consonancia con el comportamietno tanto de productos como de proveedores.
El modelo propuesto presenta una forma razonable para el tratamiento de la incertidumbre en la gestión de los inventarios mediante la aplicación de la modelación-económico matemáticas.
Es aplicable tanto a entidades comerciales y de servicios como a empresas productivas, permitiendo arribar a políticas de inventario económica en términos de costos, con demanda, costo de ordenar, costo de conservar y tiempo de entrega del proveedor en condiciones de incertidumbre.
La propuesta permite simplificar la cantidad de información y de tiempo necesarios a la hora de trabajar con los modelos probabilistas, los cuales requieren de series de tiempo que le permitan realizar pronósticos con un alto grado de certeza, y de información confiable referida a las desviaciones estándar, para así asegurar inventarios de seguridad que respondan a las necesidades de la empresa, y no incurrir en altos costos por este concepto.
Acevedo, J. A., & Gómez, M. (2010). La logística moderna en la empresa. La Habana: Félix Varela.
Asencio Cristóbal, L., González Asencio E, & Lozano Robles , M. (2017). El inventario como determinante en la rentabilidad de las distribuidoras farmacéuticas. Revista de Ciencias de la Administración y Economía, 231-250.
Bustelo de la Casa, A. (2018). Tesis de Maestría. Modelos de predicción de índices de mercados de valores mediante el uso de la lógica difusa. Barcelona, España.
Gutierrez, F., Vergara , E., Rodríguez, M., & Baber, F. (2018). Un modelo de optimizacion difusa para el problema de atraque de barcos. Investigación operacional., 160-168.
Kauffman, A., Aluja, J. G., & Pirla, J. M. (1986). Introducción de la teoría de los subconjuntos borrosos a la gestión de las empresas. España: Milladoiro.
Kaufman, A., Aluja, J. G., & Barre, R. (1987). Técnicas operativas de gestión para el tratamiento de la incertidumbre. . España: Hispano Europea.
Kaufmann, A., & Aluja, J. G. (1990). Las matemáticas del azar y de la incertidumbre: elementos básicos para su aplicación en economía. España: Centro de Estudios Ramón Areces.
Morrillas Raya, A. (2006). Introducción al análisis de datos difusos. Depto. de Estadística y Econometría. . Málaga, España: Dpto. de Estadística y Econometría. Universdiad de Málaga. Recuperado el 23 de junio de 2018, de www. eumed. net/libros/2006b/amr/
Oramas Santos, O. (2014). La gestión de inventarios en condiciones de incertidumbre.Tabajo de diploma. La Habana, Cuba.
Ortiz Torres, M. (2012). GISECOM. UN procedimiento eficiente para la getión de inventario em empresas comerciales y de servicios. Observatorio de la Economía Latinoamericana, 176.
Ortiz Torres, M., & Oramas Santos, O. (2015). La lógica difusa en la gestión de la cadena de suministros/The fuzzy sets in the supply chain management/A logica fuzzy na gestao da cadeia de abastecimento. Gestión & Desarrollo, 12(1), 53-68.
Rondón Casas, E., Farreras Noguer, M., & Linares, M. S. (2015). El Número Borroso Triangular “Ratio Acid-Test Mínima”.
Stevenson, W., & Hojati, M. (2001). Production Operation Management. Canadá: Mc Graw-Hill. Ryerson Limited.
1. Master en Administración de Negocios. Profesora del Departamento Ciencias Empresariales de la Facultad de Economía de la Universidad de La Habana. onailisos@fec.uh.cu
2. Doctora en Ciencias. Profesora Titular, jefa del Departamento Ciencias Empresariales de la Facultad de Economía de la Universidad de La Habana. maritza@fec.uh.cu
3. Rector Universidad Ecotec. Escuela de Postgrado. Doctor en Ciencias Económicas. Profesor Titular Principal, Universidad ECOTEC. Profesor Titular, Universidad de Especialidades Espíritu Santo. fmarquez@ecotec.edu.ec
4. Tarjeta de estiba. Documento primario donde se controlan las entradas y salidas de inventario por producto, consignándose la fecha y la cantidad recibida o emitida.
5. Kioskos. Puntos de ventas pequeños que se ubican en diversos puntos del territorio en el municipio y que se encarga de expender mercancías de alto consumo, con esto se garantiza acercar la oferta al consumidor final.
6. El desarrollo del ABC multicriterio puede ser consultado en: Ortiz, M. (2004). Procedimiento para la gestión de inventarios en empresas comerciales y de servicios (GISERCOM). Tesis Doctoral. La Habana, Cuba.
[Índice]
revistaespacios.com

Esta obra está bajo una licencia de Creative Commons
Reconocimiento-NoComercial 4.0 Internacional