ISSN 0798 1015

Vol. 40 (Nº 41) Año 2019. Pág. 22

Acceso a la información en el libro de texto de matemática de primer año en educación primaria en Chile

Access to information in the first grade mathematics textbook of primary education in Chile

GUTIÉRREZ-SALDIVIA, Ximena 1; DÍAZ-LEVICOY, Danilo 2; BARRÍA NAVARRO, Cecilia 3 y SALGADO-ORELLANA, Norma 4

Recibido: 30/07/2019 • Aprobado: 06/11/2019 • Publicado 25/11/2019

Contenido

1. Introducción

2. Diseño Universal para el Aprendizaje

3. Metodología

4. Conclusiones

Referencias bibliográficas

1. Introducción

El libro de texto es una herramienta pedagógica que cuenta con un reconocido prestigio y tradición en las aulas (Braga y Belver, 2016), pues permite la implementación de las directrices curriculares. En las últimas décadas, el análisis de los libros de texto se ha convertido en un tema de interés para la comunidad científica de Educación Matemática, consolidándose como línea de investigación (Gómez, 2011). Así, lo demuestran investigaciones actuales que analizan libros de texto desde la Didáctica de la Matemática (Batanero, Gea, Díaz-Levicoy y Cañada, 2015; Cárcamo, Díaz-Levicoy y Ferrada, 2018; Cobo y Batanero, 2004; Díaz-Levicoy, Ferrada, Salgado-Orellana y Guerrero-Contreras, 2019; Díaz-Levicoy, Ferrada, Salgado-Orellana y Vásquez, 2019; Díaz-Levicoy, Giacomone y Arteaga, 2017; Díaz-Levicoy, Osorio, Arteaga y Rodríguez-Alveal, 2018; Ferrada,  Díaz-Levicoy y  Salgado-Orellana, 2018). Sin embargo, son escasos los estudios que analicen los libros de texto desde la Educación Matemática Inclusiva.

En este contexto, la producción científica sobre Educación Matemática Inclusiva se centra principalmente en el aprendizaje de estudiantes con necesidades educativas especiales (Meneghello, Meneghello y de Mello, 2013). Ejemplo de esto son los trabajos de Delabona y Civardi (2016), que estudiaron el dominio de conceptos geométricos de niños con síndrome de Asperger, y el de Yokoyama (2017), que investiga la evolución del concepto de número en una adolescente con síndrome de Down. Otros autores han realizado estudios teóricos sobre la enseñanza de la matemática de estudiantes sordos (Pinheiro y Rosa, 2016), la enseñanza de la matemática e inclusión en Educación Infantil (Alencar y Silva, 2017), entre otros.

En Chile, durante los últimos años ha aumentado la producción científica sobre inclusión educativa (Apablaza, 2014; Espinosa y Valdebenito, 2016; Queupil y Durán, 2018). Sin embargo, los estudios sobre Educación Matemática Inclusiva aún son escasos. Entre ellos, destacamos el estudio de Howard-Montaner, San Martin, Salas-Guzmán, Blanco-Vargas y Díaz-Cárcamo (2018), quienes exploraron las oportunidades de aprendizaje de la matemática que ofrecen las escuelas especiales a estudiantes con discapacidad intelectual. Además, destacamos el estudio de Munoz-Soto et al. (2016), quienes presentan el diseño y validación de un objeto de aprendizaje para dispositivos táctiles que tiene como objetivo potenciar el pensamiento lógico matemático en niños con trastornos del espectro autista. Las consideraciones anteriores motivan el desarrollo de este estudio, que tiene por objetivo analizar la accesibilidad a la información en el libro de texto de matemática de primer curso de Educación Primaria en Chile. Para el análisis seleccionamos el enfoque del Diseño Universal para el Aprendizaje (DUA), porque el Ministerio de Educación de Chile, por medio del Decreto 83 (MINEDUC, 2015), establece que los centros educativos de infantil y primaria deben promover prácticas de enseñanza inclusivas y diversificadas desde este enfoque.

En síntesis, este trabajo aportará información relevante con respecto a la accesibilidad de los libros de texto que proporciona el MINEDUC desde la perspectiva del DUA, como también permitirá reflexionar sobre el uso de esta herramienta pedagógica en contextos de aulas diversas.

El Diseño Universal para el Aprendizaje (DUA) surge a partir del movimiento del Diseño Universal (DU). El DU se origina desde la arquitectura en la década de los 70, con Ron Mace de la Universidad de Carolina del Norte en Estados Unidos. El DU propone el diseño de productos y entornos que puedan ser utilizados por todas las personas, sin necesidad de adaptación (Alba-Pastor, 2016; Universal Design Institute [UDI], 2018). Desde esta perspectiva, en el ámbito de la educación, se propone el DUA, entendido como un marco curricular y didáctico basado en los conocimientos de las neurociencias sobre el aprendizaje (Rose y Meyer, 2002). Este enfoque busca generar un currículo que responda adecuadamente a la diversidad natural presente en las salas de clase (Rose y Meyer, 2002).

La importancia del DUA radica en orientar la práctica educativa, ya que proporciona flexibilidad en la presentación de la información, en las formas en que los estudiantes dan a conocer sus aprendizajes, y en las formas en que se implican en el proceso de enseñanza-aprendizaje, reduciendo las barreras en el logro de estos (Rose, 2016).

En Estados Unidos, las investigaciones del Center for Applied Special Technology (CAST) han demostrado que las barreras en el aprendizaje no son inherentes al estudiante, sino que surgen en la interacción de estos con los materiales y métodos de enseñanza (Meyer, Rose y Gordon, 2014). De esta forma, el DUA surge como una estrategia de respuesta a la diversidad. El CAST (2013) señala que es un enfoque para diseñar currículos accesibles para que todos los estudiantes puedan desarrollar conocimientos, habilidades, motivación e implicación con el aprendizaje.

Rose y Meyer (2002) plantean que son tres las acciones básicas del cerebro durante el aprendizaje, las que tienen relación con las redes neuronales de reconocimiento, estratégicas y afectivas. El DUA se estructura - a partir de estas tres redes neuronales- en 3 principios fundamentales, 9 pautas y 31 puntos de verificación. Estas estrategias tienen como objetivo minimizar las barreras del currículo y maximizar las posibilidades de aprendizaje de todos los estudiantes (Meyer, Rose y Gordon, 2014).  En la Tabla 1 se indica la relación que existe entre los principios, las redes neuronales y los componentes del diseño curricular desde el rol del estudiante.

Tabla 1
Relación entre principios del DUA, redes
neuronales y componentes del diseño curricular

Cabe destacar que en este trabajo nos centramos en el principio II, que se relaciona con el componente del diseño curricular qué se enseña y qué se aprende. Este principio se basa en la idea en que todas las personas perciben y comprenden la información de diferentes maneras, por esto se requiere enseñar utilizando múltiples formas de representación de la información (Blanco, Sánchez y Zubillaga, 2016).

Consideramos este principio, para analizar el libro de texto de matemática del primer curso de Educación Primaria, porque nos ofrece opciones para indagar si todos los estudiantes perciben y comprenden los contenidos presentados, es decir, su nivel de accesibilidad.

En la Tabla 2 presentamos la estructura del principio II, el que está conformado por tres pautas y doce puntos de verificación.  

Tabla 2
Estructura del principio II: Proporcionar
múltiples formas de representación

En resumen, el enfoque DUA nos aporta los elementos teóricos para analizar la accesibilidad a la información en los libros de texto desde la perspectiva de la Educación Matemática Inclusiva.

Esta investigación es de tipo cuantitativa y de nivel descriptivo (Hernández, Fernández y Baptista, 2010), donde analizamos el acceso a la información en el libro de texto de matemática de primer curso de Educación Primaria (Cortés, 2017) que proporciona el MINEDUC a los centros educativos públicos y particulares subvencionados.

Para la recolección de los datos, utilizamos el instrumento para evaluar el acceso a la información en libros de texto de matemática en Educación Primaria, cuyo proceso de diseño, validación y pilotaje se describen en Díaz-Levicoy, Salgado-Orellana, Gutiérrez-Saldivia y Barría (2018).  Este instrumento (ver anexo) consta de tres dimensiones y 37 indicadores que responden a los aspectos teóricos del DUA, específicamente al principio II (Tabla 3).

Tabla 3
Síntesis instrumento de evaluación

La muestra del estudio estuvo constituida por 84 lecciones del libro de texto de matemática de primer curso, de las cuales 49 corresponden al tema de números (58,3%), 18 al estudio de geometría y medición (21,4%), 10 al estudio de la estadística (11,9%) y 7 al estudio de patrones y algebra (8,3%).  En este análisis, cada lección del libro de texto constituye un elemento de estudio, donde se consideró la presencia/ausencia de cada indicador del instrumento, los que se ingresaron a una hoja de cálculo Excel, para su posterior análisis descriptivo.

4.1. Proporcionar opciones para la comprensión

En la Tabla 4 mostramos los resultados del análisis del libro de texto del primer curso de primaria con respecto a la dimensión 1 (proporcionar opciones para la comprensión). Se observa, que en las lecciones del libro predominan estrategias correspondientes a la sub-dimensión 1.2 asociada a destacar patrones, características fundamentales, ideas principales y relaciones (66,4%).  Dentro de esta sub-dimensión predominan los indicadores 1.2.1 y 1.2.2 relacionados con destacar tanto los contenidos principales a aprender (95,2%), como las ideas principales (89,3%) que se presentan en las lecciones en bloques de textos y párrafos resumen. Además, se observa que predominan estrategias asociadas al indicador 1.1.1 (90,5%) e indicador 1.3.1 (81%), vinculadas a que las lecciones incluyen actividades para explorar los conocimientos previos de los estudiantes y a la organización progresiva de las actividades según la complejidad de los contenidos.

Cabe destacar que las estrategias mencionadas favorecen la comprensión de los contenidos matemáticos en libros de texto. Sin embargo, no son suficientes, ya que el libro de texto utiliza estrategias que no respondan necesariamente a múltiples formas de representación de los contenidos. Esto se observa en el análisis al constatar que el indicador 1.1.2 (10,7%) y 1.1.3 (4,8%) se identifican escasamente en las lecciones, donde las tareas de activación de conocimientos previos no incluyen organizadores gráficos ni se complementan con el uso de recursos digitales. Además, se observa en las lecciones escasas estrategias asociadas a la sub-dimensión 1.4 (25,6%), es decir, que permitan la transferencia y generalización de los aprendizajes matemático. Como por ejemplo el indicador 1.4.2 (0%) asociado al uso de listas de comprobación para que los estudiantes revisen lo aprendido, o el indicador 1.4.5 (1,2%) que señala que en la lección se utilizan estrategias nemotécnicas para recordar información.

Tabla 4
Frecuencia (y porcentaje) de la dimensión 1
(proporcionar opciones para la comprensión)

A modo de ejemplo, en la Figura 1 se muestra un extracto de una lección del libro de texto donde se identifican tres estrategias de la dimensión 1 (proporcionar opciones para la comprensión). La primera estrategia asociada al indicador 1.2.1 que consiste en explicitar en la lección el contenido que se aprenderá; la segunda estrategia correspondiente al indicador 1.1.1, donde se presenta una actividad que permite activar el conocimiento previo; y la tercera estrategia se vincula con el indicador 1.2.2, pues se utiliza en la lección un bloque de texto para destacar información relevante. Cabe mencionar que estas estrategias son las más frecuentes en las lecciones del libro de texto analizado.

Figura 1
Estrategias para proporcionar opciones
para la comprensión (Cortés, 2017, p. 14)

3.2 Proporcionar opciones para el lenguaje, las expresiones matemáticas y los símbolos

En la Tabla 5 se presentan los resultados del análisis del libro de texto respecto a la dimensión 2 (proporcionar opciones para el lenguaje, las expresiones matemáticas y los símbolos). A nivel general, se observa que en las lecciones del libro de texto predominan estrategias de la sub-dimensión 2.2 (68,7%) relacionadas con clarificar la sintaxis y la estructura. Específicamente esto se evidencia en el indicador 2.2.1 (96,4%) asociado a que las instrucciones de las lecciones explicitan la acción que deben realizar los estudiantes; y en el indicador 2.2.2 (100%) donde se menciona que los enunciados de los problemas planteados presentan la información necesaria para su resolución, ya que se explicitan los datos y la(s) pregunta(s) para su resolución.

Tabla 5
Frecuencia (y porcentaje) de la dimensión 2 (proporcionar opciones
para el lenguaje, las expresiones matemáticas y los símbolos)

Cabe destacar, que el análisis nos permite afirmar que las lecciones del libro de texto analizado no proporcionan variadas estrategias que favorezcan la comprensión del lenguaje y los símbolos. Por ejemplo, en las lecciones se evidencian escasas estrategias de la sub-dimensión 2.3 (8,3%) para facilitar la decodificación de textos, notaciones matemáticas y símbolos. En relación con esto, identificamos escasa presencia del indicador 2.3.1 (4,8%) que hace referencia el uso de pictogramas o iconos en las lecciones; además el indicador 2.3.4 (13,1%), ya que no se explicitan con frecuencia los símbolos y notaciones matemáticas. Asimismo, se observa ausencia de estrategias de la sub-dimensión 2.4 (0%) asociada a promover la comprensión entre diferentes idiomas, pues no se incorpora una alternativa lingüística a la lengua castellana, a pesar de que en las escuelas chilenas conviven estudiantes indígenas, inmigrantes y no indígenas.

Un libro de texto para ser accesible debe partir de la premisa de que no todas las personas comprendemos de la misma manera los símbolos y las palabras. En este contexto, uno de los desafíos del libro de texto analizado es la incorporación de estrategias asociadas al indicador 2.5.1 (7,1%) que señala que la lección presenta un mismo contenido por medio de múltiples formas. Somos conscientes que el libro de texto es un recurso fijo. Sin embargo, sostenemos que las lecciones deben promover el uso de recursos adicionales al texto.

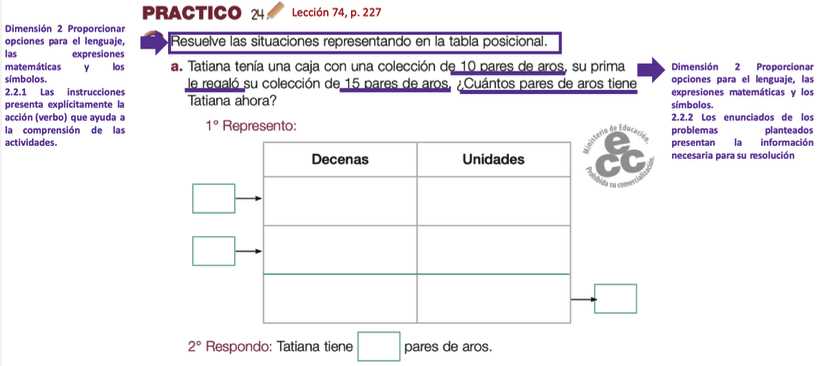
En la Figura 2 se muestra un extracto de una lección del libro de texto analizado, donde se identifican estrategias de la sub-dimensión 2.1 correspondiente a facilitar la comprensión de la sintaxis y la estructura. La primera estrategia corresponde al indicador 2.2.1 que consiste en explicitar en la instrucción de la lección el verbo (acción), lo que permite al estudiante identificar lo que debe realizar. Mientras que la segunda estrategia que se identifica corresponde al indicador 2.2.2 donde el enunciado del problema matemático incluye explícitamente la información para su resolución (datos y pregunta). Cabe destacar que cuando las reglas y estructuras no son explícitas se puede ver afectada la comprensión de la información.

Figura 2
Estrategias para clarificar la sintaxis
y la estructura (Cortéz, 2017, p. 227)

3.3. Proporcionar diferentes opciones para la percepción

En la tabla 6 se presentan los resultados respecto a la dimensión 3 (proporcionar opciones para la percepción). De acuerdo al análisis podemos afirmar que el libro de texto analizado, en su formato impreso, no ofrece múltiples opciones para la percepción de la información. Esto se evidencia por la ausencia de estrategias asociadas a la sub-dimensión 3.1 (0%) que hace referencia a que las lecciones deben ofrecer opciones que permitan la modificación y personalización en la presentación de la información; y la ausencia de estrategias de la sub-dimensión 3.2 asociada a ofrecer alternativas para la información visual. Por ejemplo, se observa ausente el indicador 3.2.1 (0%), pues las lecciones no incluyen una descripción textual o auditiva de la información que se presenta en imágenes, gráficos o tablas.

Tabla 6
Frecuencia (y porcentaje) de la dimensión 3
(proporcionar opciones para la percepción)

Analizar el libro de texto de primer curso de matemática para Educación Primaria, nos permite un primer acercamiento sobre la accesibilidad a la información que entrega esta herramienta pedagógica en el contexto chileno.  Mediante este análisis, observamos que, si bien el libro de texto no está diseñado desde el marco teórico del DUA, la autora del libro de texto y los editores realizan un esfuerzo de incluir estrategias que permiten proporcionar opciones alternativas de representación de la información de los contenidos matemáticos. Específicamente, evidenciamos un predominio de estrategias asociadas a la dimensión 1 proporcionar opciones para la comprensión de los temas en estudio. Desde la perspectiva de la Educación Matemática Inclusiva se hace necesario intencionar, en los libros de texto, estrategias que ayuden a todos los estudiantes a decodificar el lenguaje, las expresiones matemáticas y los símbolos, debido a que cada uno tiene diferentes formas para acceder a la información. Por ejemplo, el signo igual (=) en matemática puede ser interpretado de distintas maneras, ya sea como una invitación a hacer algo, operar sobre los números o como un símbolo relacional (Ramírez, 2010). Es por ello, la importancia de clarificar a través de significados alternativos los elementos semánticos (CAST, 2011), siendo necesario explicitar en el libro de texto los significados según los contenidos y habilidades que se enseñen.

Este estudio nos permite sostener que el libro de texto analizado, a pesar de ser un recurso que presenta los contenidos de manera fija e impresa, tiene posibilidades de ser una herramienta pedagógica de mayor accesibilidad a la información. Para esto se requiere que las diversas entidades encargadas de diseñar los planes de estudios, los editores y autores de libros de texto consideren en sus propuestas enfoques de estrategias diversificadas como el DUA y estándares de accesibilidad, como por ejemplo los estándares de textos digitales Daisy u otros.

 Finalmente, para que la información del libro de texto sea más accesible para todos los estudiantes, es clave que el formato impreso sea complementado con una versión digital del libro (no basta con un formato PDF) o una plataforma virtual que proporcione opciones que permitan la personalización de la información y alternativas a la información visual, de manera que el libro de texto se pueda modificar a las características perceptivas de cada estudiante.

ALBA-PASTOR, C. (2016). Diseño universal para el aprendizaje: educación para todos y prácticas de enseñanza inclusivas. Madrid: Morata.

ALENCAR, E. y SILVA, R. J. (2017). A literatura infantil na educação matemática inclusiva. Educação Matemática em Revista-RS, 3(18), 68-74.

APABLAZA, M. (2014). Representaciones sociales de profesores respecto de la diversidad escolar en relación a los contextos de desempeño profesional, prácticas y formación inicial. Estudios Pedagógicos, 40(1), 7-24.

BATANERO, C., GEA, M. M., DÍAZ-LEVICOY, D. y  CAÑADAS, G. R. (2015). Objetos matemáticos ligados a la regresión en los textos españoles de bachillerato. Educación matemática, 27(2), 9-35.

BLANCO, M., SÁNCHEZ, P. y ZUBILLAGA, A. (2016). El modelo del Diseño Universal para el Aprendizaje: principios, pautas y propuestas para la práctica. En C. Alba-Pastor, (Eds.), Diseño universal para el aprendizaje: educación para todos y prácticas de enseñanza inclusivas (pp. 25-58). Madrid: Morata.

BRAGA, G. y BELVER, J. L. (2016). El análisis de libros de texto: una estrategia metodológica en la formación de los profesionales de la educación. Revista Complutense de Educación, 27(1), 199-218.

CÁRCAMO, M., DÍAZ-LEVICOY, D. y FERRADA, C. (2018). Los ejemplos en la enseñanza de las ecuaciones en libros de texto de Educación Primaria. REMAT: Revista Eletrônica da Matemática, 4(1), 38-54.

CAST. (2011). Universal Design for Learning Guidelines versión 2.0. Wakefield, MA: CAST.

CAST. (2013). Pautas sobre el Diseño Universal para el Aprendizaje (DUA) (Trad. C. Alba Pastor, P. Sánchez, J. M. Sánchez-Serrano y A. Zubillaga). Wakefield, MA: Autor.

COBO MERINO, B. y  BATANERO BERNABEU, C. (2004). Significado de la media en los libros de texto de secundaria. Enseñanza de las Ciencias, 22(1), 005-18.

CORTÉS, C. (2017). Texto de la estudiante matemática 1º básico. Santiago: Cal y Canto.

DELABONA, S. C. y CIVARDI, J. A. (2016). Conceitos geométricos elaborados por um aluno com síndrome de asperger em um laboratório de matemática escolar. Revista Paranaense de Educação Matemática, 5(9), 203-232.

DÍAZ-LEVICOY, D., FERRADA, C., SALGADO-ORELLANA, N. y GUERRERO-CONTRERAS, O. (2019). Las actividades de evaluación en los textos escolares de Educación Básica en Chile. Trilhas Pedagógicas, 9(11), 28-44.

DÍAZ-LEVICOY, D., FERRADA, C., SALGADO-ORELLANA, N. y VÁSQUEZ, C. (2019). Análisis de las actividades evaluativas sobre estadística y probabilidad en libros de texto chilenos de Educación Primaria. Premisa, 21(80), 5-21.

DÍAZ-LEVICOY, D., OSORIO, M., ARTEAGA, P. y RODRÍGUEZ-ALVEAL, F. (2018). Gráficos estadísticos en libros de texto de matemática de Educación Primaria en Perú. BOLEMA. Boletim de Educação Matemática, 32(61), 503-525.

DÍAZ-LEVICOY, D., SALGADO-ORELLANA, N., GUTIÉRREZ-SALDIVIA, X. y BARRÍA, C. (2018). Validación y pilotaje de un instrumento para evaluar el acceso a la información en libros de texto de matemática en Educación Primaria. Revista Paranaense de Educação Matemática, 7(13), 7-32.

DÍAZ-LEVICOY, D., GIACOMONE, B. y ARTEAGA, P. (2017). Caracterización de los gráficos estadísticos en libros de texto argentinos del Segundo Ciclo de educación primaria. Profesorado. Revista de Curriculum y Formación de Profesorado, 21(3), 299-326.

ESPINOSA, J. y VALDEBENITO, V. (2016). Explorar las concepciones de los docentes respecto al proceso de educación inclusiva para la mejora institucional. Revista Latinoamericana de Educación Inclusiva, 10(1), 195-213.

FERRADA, C., DÍAZ-LEVICOY, D. y SALGADO-ORELLANA, N. (2018). Análisis de actividades sobre educación financiera en libros de texto chilenos de Educación Primaria. TANGRAM. Revista de Educação Matemática, 1(4), 41-65.

GÓMEZ, B. (2011). El análisis de manuales y la identificación de problemas de investigación en Didáctica de las Matemáticas. PNA, 5(2), 49-65.

HERNÁNDEZ, R., FERNÁNDEZ, C. y BAPTISTA, P. (2010). Metodología de la Investigación. México: McGraw Hill.

HOWARD-MONTANER, S., SAN MARTIN, C., SALAS-GUZMÁN, N., BLANCO-VARGAS, P. y DÍAZ- CÁRCAMO. (2018).  Oportunidades de aprendizaje en matemáticas para estudiantes con discapacidad intelectual. Revista Colombiana de Educación, (74), 197-219

MENEGHELLO, A., MENEGHELLO, M. y DE MELLO, S. (2013). A Educação Matemática Inclusiva no Brasil: uma análise baseada em artigos publicados em revistas de Educação Matemática. Revista Brasileira de Ensino de Ciência e Tecnologia, 6(2) 1-22.

MEYER, A., ROSE, D. y GORDON, D. (2014). Universal design for learning: theory and practice. Wakefield, MA: CAST.

MINEDUC.(2015). Diversificación de la enseñanza. Decreto N°83/2015: Aprueba criterios y orientaciones de adecuación curricular para estudiantes con necesidades educativas especiales de Educación Parvularia y Educación Básica. Santiago: Unidad Educación Especial.

MUNOZ-SOTO, R., BECERRA, R., NOEL, R., BARCELOS, T., VILLARROEL, R., KREISEL, S. y CAMBLOR, M. (2016). Proyect@ Matemáticas: A Learning Object for Supporting the Practitioners in Autism Spectrum Disorders. En M. Chacón (Ed.), XI Latin American Conference on Learning Objects and Technology: proceedings, Actas..., San Carlos: Instituto Tecnológico de Costa Rica.

PINHEIRO, R. C. y ROSA, M. (2016). Uma perspectiva etnomatemática para o processo de ensino e aprendizagem de alunos Surdos. Revista Paranaense de Educação Matemática, 5(9), 56-83.

QUEUPIL, J. P. y DURÁN DEL FIERRO, F. (2018). El principio de inclusión: similitudes y diferencias en la educación escolar y superior en Chile. Revista latinoamericana de educación inclusiva, 12(1), 111-128.

RAMÍREZ, M. (2010). Interpretaciones del signo igual. Un estudio de libro de texto.  (Trabajo fin de Máster). Universidad Complutense de Madrid, Madrid.

ROSE, D.H. (2016). Prólogo. En C. Alba-Pastor, (ed.), Diseño Universal para el aprendizaje: Educación para todos y prácticas de enseñanza inclusiva (pp. 9-10). Madrid: Morata.   

ROSE, D. H. y MEYER, A. (2002). Teaching every student in the digital age: Universal Design for Learning. Alexandria, VA: Association for Supervision and Curriculum Development.

UDI. Aboud UDI. Recuperado (12.01.2018) de http://udinstitute.org/aboutudi.php

YOKOYAMA, L. A. (2017). Primeiras noções numéricas de uma adolescente com síndrome de Down através de materiais multissensoriais. Educação Matemática em Revista-RS, 3(18), 75-82.

Fuente: Díaz-Levicoy, Salgado-Orellana,
Gutiérrez-Saldivia y Barría (2018)

1. Máster Universitario en Intervención Psicopedagógica por la Universidad de Granada, Doctoranda en Educación en Consorcio, Universidad Católica de Temuco. Académica planta temporal Carrera de Pedagogía en Educación Diferencial, Facultad de Educación, Departamento de Infancia y Educación Básica, Universidad Católica de Temuco. Email: xgutierrez.saldivia@gmail.com

2. Doctor en Ciencias de la Educación. Académico Departamento de Matemática, Física y Estadística, Facultad de Ciencias Básicas, Universidad Católica del Maule. E-mail: dddiaz01@hotmail.com

3. Máster en integración de personas con discapacidad por la Universidad de Salamanca. Académica Carrera de Pedagogía en Educación Diferencial, Facultad de Educación, Departamento de Infancia y Educación Básica, Universidad Católica de Temuco. Email: cbarria@uct.cl

4. Máster Universitario en Intervención Psicopedagógica por la Universidad de Granada, Doctoranda en Ciencias de la Educación, Departamento de Métodos de Investigación y Diagnóstico en Educación, Universidad de Granada. E-mail: nsalgado@correo.ugr.es