ISSN 0798 1015

Vol. 40 (Nº 41) Año 2019. Pág. 20

Diseño y validación de un cuestionario para evaluar la comprensión de gráficos estadísticos en futuras educadoras de párvulos

Design and validation of a questionnaire to evaluate the understanding of statistical graphs in prospective preschool teachers

SAMUEL, Marjorie 1; DÍAZ-LEVICOY, Danilo 2 y RODRÍGUEZ-ALVEAL, Francisco 3

Recibido: 08/08/2019 • Aprobado: 20/11/2019 • Publicado 25/11/2019

Contenido

1. Introducción

2. Marco teórico

3. Metodología

4. Resultados

5. Conclusión

Referencias bibliográficas

Anexos: Gráficos estadísticos para estudiantes de Educación Parvularia

1. Introducción

En el último tiempo, la estadística se ha convertido en un área fundamental para otras disciplinas y para la vida cotidiana de los ciudadanos, dado que tienen acceso a abundante información de tipo estadística, la que deben interpretar adecuadamente y de manera crítica, para  comprender el mundo que les rodea y tomar decisiones acertadas (Díaz-Levicoy, Batanero, Arteaga y López-Martín, 2015). Mucha de esta información viene por medio de gráficos estadísticos, especialmente en los medios de comunicación y la vida cotidiana (Ainley, Pratt y Nardi, 2001; Cavalcanti, Natrielli y Guimarães, 2010). Esta relevancia los hace ser parte de la cultura estadística (Arteaga, Batanero, Cañadas y Contreras, 2011; Cazorla y Utsumi, 2010; Gal, 2002; English y Watson, 2015; Lopes, 2004; Watson, 2013).

En diferentes países, vemos como la enseñanza de la estadística, y de los gráficos estadísticos en particular, se propone desde los primeros cursos de Educación Primaria, por ejemplo, Brasil (MEC, 1997; MEC, 2017), Chile (MINEDUC, 2012), España (MECD, 2014), o Perú (MINEDU, 2009, 2016), impactando en la organización de los procesos de enseñanza y aprendizaje, la formación inicial y continua del profesorado, y el diseño de los materiales de apoyo a la instrucción (libros de texto, cuadernillos de trabajo, plataformas, etc.).

En el caso de Educación Infantil, la literatura muestra la factibilidad en trabajar aspectos básicos de la estadística desde edades tempranas (e.g., Alsina, 2012; Alsina y Vásquez, 2017; Cervilla, Arteaga y Díaz-Levicoy, 2014; Vásquez y Alsina, 2019; Vásquez, Díaz-Levicoy, Coronata y Alsina, 2018). Además, es un tema que se incluye dentro del itinerario formativo de las futuras Educadoras de Párvulos. Es decir, es necesario dotar a las futuras Educadoras de Párvulos del conocimiento didáctico y disciplinario para generar las situaciones de aprendizaje de los elementos básicos de estadística (Díaz-Levicoy, Sepúlveda, Vásquez y Opazo, 2017), propio de las edades tempranas.

De acuerdo con las consideraciones anteriores, en este artículo, nos proponemos el objetivo de describir el proceso de diseño y validación de un instrumento que evalúe el conocimiento pedagógico y del contenido sobre gráficos estadísticos de futuras Educadoras de Párvulos.

En lo que sigue, describimos el modelo de conocimiento que utilizaremos como marco teórico y que sustenta muestro estudio, siguiendo con la descripción del proceso de diseño y validación del instrumento, para finalizar con las conclusiones.

El conocimiento que deben tener los profesores para enseñar matemática, o estadística en nuestro caso, ha sido objeto de investigación y reflexión por diversos autores (e.g., Ball y Bass, 2000; Ball, Hill y Bass, 2005; Ball, Lubienski y Mewborn, 2001; Ball, Thames y Phelps, 2008; Carrillo, Climent, Contreras y Muñoz-Catalán, 2013; Godino, 2009; Gómez, 2007; Hill, Rowan y Ball, 2005; Pino-Fan y Godino, 2015; Ponte y Chapman, 2008), motivados por los trabajos de Shulman (1986, 1987), han propuesto, desde diversas perspectivas epistemológicas del conocimiento y de la educación, modelos que han de describir, valorar y guiar los procesos de enseñanza y aprendizaje, relevando el conocimiento y el uso de este en las distintas situaciones del enseñar.

En este contexto, la indagación sobre el conocimiento del contenido matemático, está configurando una agenda internacional de investigación apoyada en la noción de conocimiento matemático para enseñar (Mathematical Knowledge for Teaching - MKT) (Ball, Thames y Phelps, 2008; Carrillo, Climent, Contreras y Muñoz-Catalán, 2013; Varas, Lacourly, López y Giaconi, 2013), planteando que este conocimiento juega un papel importante, porque permite que los profesores se anticipen a los posibles conflictos de significado que emergen durante la solución de tareas matemáticas por parte del estudiante y prever la complejidad del proceso de enseñanza. En este sentido, el MKT introduce la noción de conocimiento matemático para la enseñanza, asumiéndola como “el conocimiento matemático que utiliza el profesor en el aula para producir instrucción y desarrollo en el alumno” (Hill, Ball y Schilling, 2008, p. 374). Este tipo de conocimiento caracteriza al profesor, de cualquier nivel educativo, que enseña matemática.

En este ámbito, diversos autores (Ball, 1990; Ball, Thames y Phelps, 2008; Hill y Ball, 2004; Ball, Lubienski y Mewborn, 2001) han aportado información sobre la naturaleza y características del conocimiento que debería tener un profesor que enseña matemática, enfatizando en dos tipos: el conocimiento de la matemática y el conocimiento pedagógico de la matemática. A partir de este modelo plantean una conceptualización de subdominios o categorías (Figura 1), las que se describen en la Tabla 1.

Figura 1
Conocimiento matemático para la enseñanza

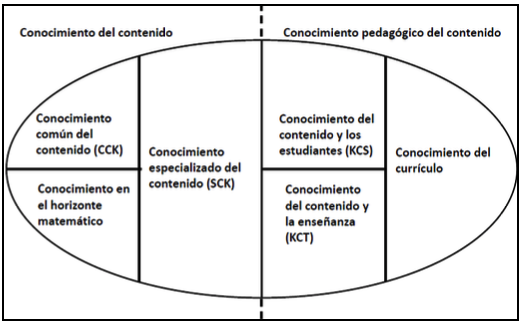
(Hill, Ball y Schilling, 2008, p. 403)

------

Tabla 1
Descripción de los subdominios del modelo de conocimiento
matemático para la enseñanza del Ball y cols.

Dichas descripciones fueron las consideradas para diseñar un cuestionario para evaluar el conocimiento sobre gráficos estadísticos de futuras educadoras de párvulos en el contexto chileno.

Para dar cumplimiento al objetivo de este documento, en primer lugar, se revisaron y adaptaron ítems de estudios de comprensión de gráficos estadísticos en estudiantes chilenos de Educación Básica (Díaz-Levicoy, 2018), y sobre la lectura de tablas estadísticas por estudiantes chilenos de Educación Básica (Díaz-Levicoy, Morales, Cruz y López-Martín, 2016; Sepúlveda, Díaz-Levicoy y Jara, 2018) y por futuras educadoras de párvulos (Díaz-Levicoy, Sepúlveda, Vásquez y Opazo, 2017). Además, se crean otros que aborden aspectos que no se han considerado en los estudios previos, producto del marco teórico utilizado o la naturaleza de la muestra.

Luego del proceso de depuración y selección, se decidió que el instrumento conste de 7 ítems, un número apropiado, que aborde diferentes aspectos del conocimiento matemático para la enseñanza y que se puede responder en una sesión de clase. En la Tabla 2 especificamos el conocimiento que considera cada ítem.

Tabla 2
Tipo de conocimiento
considerado en cada ítem

Para la validación de los ítems se recurrió al método de juicio de expertos (Barraza, 2007), y que se define como “una opinión informada de personas con trayectoria en el tema, que son reconocidas por otros como expertos cualificados en éste, y que pueden dar información, evidencia, juicios y valoraciones” (Escobar-Pérez y Cuervo-Martínez, 2008, p. 29). Para este estudio, utilizamos la caracterización de experto realizado por Millman y Greene (1989), es decir, que depende del objetivo del instrumento.  En nuestro caso, son investigadores que trabajen sobre: formación de profesores de diferentes niveles y/o educadoras de párvulos y educación estadística y/o gráficos estadísticos. Finalmente, los que participaron en esta validación se seleccionaron de acuerdo con los siguientes criterios: 1) Experiencia investigativa, publicaciones y proyectos; 2) Reconocimiento por la comunidad científica; 3) Disponibilidad y motivación para participar en el proceso; 4) Imparcialidad en el proceso de investigación (Skjong y Wentworht, 2001).

En este proceso, se consideró un total de 15 posibles investigadores para que participen en la validación, a los que se contactó por medio de correo electrónico, para hacer un primer contacto, indicar el objetivo de nuestro estudio y de su participación, y ver si está dispuesto a colaborar. A los que manifestaron su intención de colaborar, se les envió una carta formal de presentación, indicando el objetivo del instrumento, la importancia de su colaboración y el agradecimiento de los investigadores (Figura 2).

Figura 2
Presentación cuestionario a expertos

En una segunda hoja se presentaron las definiciones conceptuales de las variables, que en nuestro caso corresponden a la descripción de los subdominios del modelo de conocimiento matemático para la enseñanza del Ball y cols. (Tabla 1).

En la tercera página (Figura 3), se entregan instrucciones para realizar la valoración de cada ítem (asignar puntuación), respecto de la claridad, pertinencia y relevancia. Además, se proporciona una sección para que el experto realice los comentarios que estime pertinente.

Figura 3
Indicaciones para realizar la validación

Finalmente, después de un mes, recibimos la validación de 11 investigadores, cuyos perfiles académicos e investigativos resumimos en la Tabla 3.

Tabla 3
Perfil profesional e investigador de los
expertos partícipes de la validación

El perfil y diversidad de expertos nos permite obtener una versión mejorada del instrumento (ver Anexo), cuyo proceso se describe en el siguiente apartado.

La Tabla 4 resume la puntuación (promedio, moda, desviación estándar y coeficiente de asimetría) con respecto a la claridad (se entiende sin dificultad alguna el enunciado, siendo conciso, exacto y directo), pertinencia (pertenece a la categoría) y relevancia (es apropiado para representar a la categoría específica del constructo) de cada ítem. Dichas puntuaciones promedio son todas mayores a los 4 puntos y siendo el valor más frecuente los 5 puntos (excepto en el ítem 2), evidenciando que la evaluación de los expertos es alta, lo que se corrobora con el coeficiente de asimetría negativo en cada uno de los ítems.

También, los expertos coinciden en que los ítems del instrumento son pertinentes y relevantes para la temática en estudio, dada la correlación positiva en estos criterios, cuyos coeficientes de correlación fluctúan entre 0,7 a 1,0. Salvo el ítem 5d donde la relevancia y pertinencia presenta la correlación más baja (0,39).

Tabla 4
Puntuación asignada
por los expertos

Estas puntuaciones se complementan con los comentarios realizados por los expertos y que se detallan a continuación.

4.1. Ítem 1

El primer ítem (¿Cómo definiría usted un gráfico estadístico?), que se relaciona con el conocimiento especializado del contenido, se mantiene sin modificaciones en su versión original, por su alta puntuación media y modal. Si bien es una pregunta amplia, esta decisión se apoya en el propósito que buscamos (caracterización de un gráfico) y por el comentario de un experto:

Me parece interesante que los y las estudiantes comprendan el concepto de gráfico, y qué características debe tener para que sea estadístico (Experto 4).

4.2. Ítem 2

El segundo ítem (Haga una lista considerando todos los conceptos estadísticos que usa cuando trabaja con un gráfico), relacionado con el conocimiento especializado del contenido, es valorado positivamente por los expertos (claridad: 4,3 de media y 4 de moda; pertinencia: 4,6 de media y 5 de moda; relevancia: 4,5 de media y 5 de moda), pero se modifica de acuerdo con los comentarios de los siguientes expertos:

Yo diría “conocimientos estadísticos”, y no “conceptos estadísticos” (Experto 1).

Creo que considerar “todos” los conceptos es ambicioso. Pondría “conceptos” (Experto 4).

Creo que sería más pertinente especificar un gráfico en concreto, para que se describan todos los conceptos estadísticos involucrados en él. Dependiendo del gráfico, puede haber más o menos conceptos involucrados. Ejemplo, no es lo mismo un diagrama de sectores que un diagrama de barras o un diagrama de cajas y bigotes (Experto 6).

De acuerdo con lo anterior, se elimina la palabra todos; se cambia conceptos estadísticos por conocimientos matemáticos y estadísticos; y se especifica que este ítem es en torno al gráfico de barras, por su facilidad para trabajar en las primeras edades de formación.

4.3. Ítem 3

El tercer ítem (Figura 4) se asocia al conocimiento del contenido y la enseñanza, es evaluado con una media de 4,7 y una moda de 5 para los tres criterios considerados (Tabla 4).

Figura 4
Versión sometida a juicio
de expertos del ítem 3

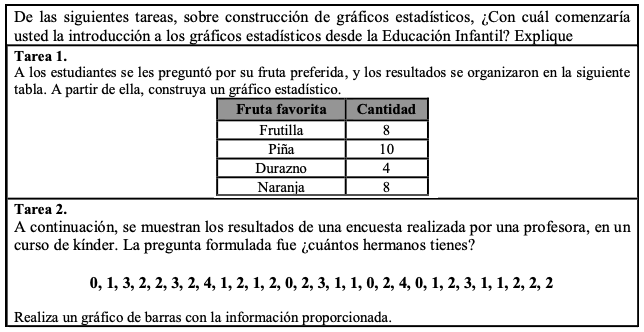
Si bien este ítem obtiene una alta valoración por parte de los expertos, el 3 realizó un comentario que consideramos pertinente, porque está en concordancia con el objetivo de nuestro instrumento y que aporta directamente a la mejora de este:

Realiza un gráfico de barras con los datos la información proporcionados (Experto 3).

Otros comentarios se han descartado por no estar en correspondencia con nuestro objetivo. Por ejemplo, dando respuesta al experto 7, los gráficos de barras son también pertinentes para trabajar en las primeras edades; o al experto 10, nuestro centro de atención es el conocimiento de las futuras educadoras de párvulos y no los niños.

Un pictograma podría ser más adecuado ya que se trata de Educación Infantil (Experto 7).

No estoy segura que todos los niños y niñas de Educación Infantil completaran con éxito la segunda tarea (Experto 10).

Además, cambiamos el contexto en que se presenta la situación, de número de hermanos a mascotas, para hacerlo más cotidiano para los niños.

4.4. Ítem 4

El cuarto ítem (Figura 5) pretende evaluar el conocimiento especializado del contenido sobre gráficos estadísticos de las futuras educadoras de párvulos, mediante preguntas de diferentes dificultades.

Figura 5
Versión sometida a juicio
de expertos del ítem 4

Las puntuaciones que han dado los expertos respecto a la claridad (4,3 de media y 5 de moda), pertinencia (4,5 de media y 5 de moda) y relevancia (4,5 de media y 5 de moda) del ítem son altas. Estas puntuaciones se acompañan de comentarios positivos como los siguientes:

Me parece un buen ítem para evaluar el conocimiento especializado del contenido ya que requiere por parte de las futuras maestras buenos niveles de comprensión gráfica que al fin y al cabo es un conocimiento que deben de tener para la enseñanza del tema (Experto 2).

Las educadoras de párvulos deben saber responder con éxito a todas las preguntas (Experto 10).

Dentro de los cambios realizados en este ítem, motivados por los expertos, está la modificación de los valores del gráfico porque en algunos casos los porcentajes de aprobación y desaprobación no suman 100; agregar los signos de interrogación en la pregunta c); y cambiar la palabra estimó por obtuvo.

El gráfico me parece confuso. A mi modo de ver, los porcentajes de aprobación y desaprobación deberían sumar, en todos los casos, el 100%, pero no ocurre así. ¿Qué pasa con el % que se omite? ¿A qué valor de la variable se refiere? (Experto 1).

El enunciado del ejercicio me lleva a error. Puede que sea una cuestión de lenguaje, pero la redacción no me queda clara. ¿El porcentaje de reprobación + el porcentaje de aprobación no suma nunca 100%? ¿Por qué? ¿De qué estamos hablando, de alumnado que reprueba y aprueba? Si es esto así, ¿por qué los porcentajes de cada mes no suman 100%? Creo que la redacción del ejercicio debe estar más contextualizado para poderse entender. Si se está valorando alguna otra opción de la variable analizada que no aparece, debería decirse… (Experto 6).

Poner interrogantes en la c) (Experto 5).

e) ¿Cuál será el porcentaje de aprobación que tendría la directora del Jardín en el décimo mes? Explique cómo lo estimó obtuvo (Experto 3).

4.5. Ítem 5

El quinto ítem (Figura 6) pretende evaluar tres subdominios del modelo de conocimiento matemático para la enseñanza (del contenido y los estudiantes, especializado del contenido, y del contenido y la enseñanza) sobre gráficos estadísticos de las futuras educadoras de párvulos.

Figura 6
Versión sometida a juicio de expertos del ítem 5

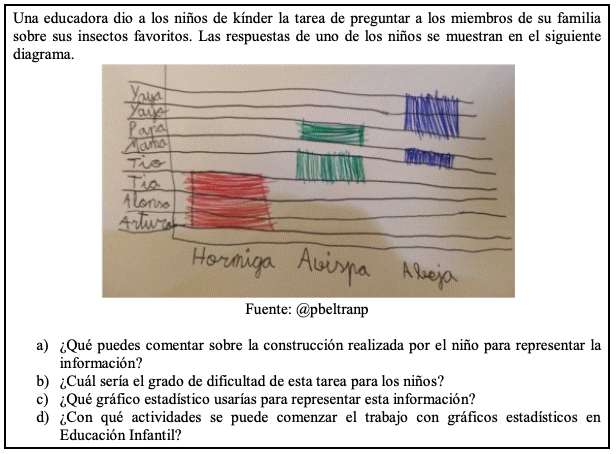
Las puntuaciones dada por los expertos son altas, todas con una media mayor a 4,2 en claridad y 4,5 en pertinencia y relevancia; y 5 de moda para todos los criterios de evaluación.

Pese a estas puntuaciones, realizamos algunas modificaciones que consideramos pertinentes de acuerdo con los comentarios de los expertos. Por ejemplo, se cambia la primera pregunta para que sea más clara y concisa; en la segunda se pide asignar una valoración tipo Likert a la dificultad de la tarea para el estudiante; en ambos casos es necesario justificar la respuesta entregada. Finalmente, la cuarta pregunta se elimina, además por su bajo coeficiente de correlación. Los comentarios de los expertos son:

5a. Me parece muy ambigua/poco clara la formulación. Sugiero que la pregunta se centre más en el conocimiento especializado del contenido. 5b. Hay que especificar más, por ejemplo a partir de un rango 1-5 (Experto 1).

Me da la sensación que la tarea 5d es como una tarea que no tiene estrecha relación con el resto de apartados ni con la imagen de la tarea 5, me da la sensación que la tarea 5d podría ser una pregunta que podría ir sola en un ítem debido a las características de la misma  (Experto 2).

En la 5b hay que poner una escala para que los participantes elijan. Se puede complementar con un campo abierto para que justifiquen su elección, pero tal como está no conviene dejarla. En la 5c poner un campo abierto para que se expliquen. La 5d la propondría como un ítem aparte, así parece estar relacionada con el resto de apartados del ítem 5 (Experto 5).

La pregunta del 5a es poco clara. Debería ser más dirigida si se espera que las maestras aporten argumentos asociados a la estadística. La pregunta 5b es poco clara. Cuando se pregunta por el grado de dificultad, se quiere preguntar por el grado de dificultad en que los niños realicen la representación gráfica o en que los niños pregunten a su familia por el tipo de insecto. Las dificultades son completamente diferentes. Además debería tenerse en cuenta la edad de los niños, la respuesta de las maestras variará en gran medida dependiendo de los niños que tengan. 5d: No veo la relación de la última pregunta con la tarea expuesta. La pregunta es tan abierta, que da pie a cualquier tipo de respuesta, ¿cómo se va a evaluar? (Experto 6).

4.6. Ítem 6

El sexto ítem (Propone un objetivo de aprendizaje para la enseñanza de los gráficos estadísticos en Educación Parvularia), que busca evaluar el conocimiento del contenido y el currículo, obtuvo una puntuación alta como se puede ver en la Tabla 4.  El cambio realizado en este ítem tiene relación con la redacción del enunciado, reemplazando propone por proponga, tal como lo sugieren los expertos:

En todo el cuestionario, ya redactaría en tercera persona y con trato de Vd. “proponga” (Experto 1).

Proponga en vez de propone (Experto 5).

Cambiar “Propone” por “Proponga” (Experto 6).

4.7. Ítem 7

El séptimo ítem (Figura 7) aborda el conocimiento del contenido y los estudiantes, y el conocimiento del contenido y la enseñanza. Los expertos asignaron puntuaciones altas para cada criterio considerado.

Figura 7
Versión sometida a juicio de expertos del ítem 7

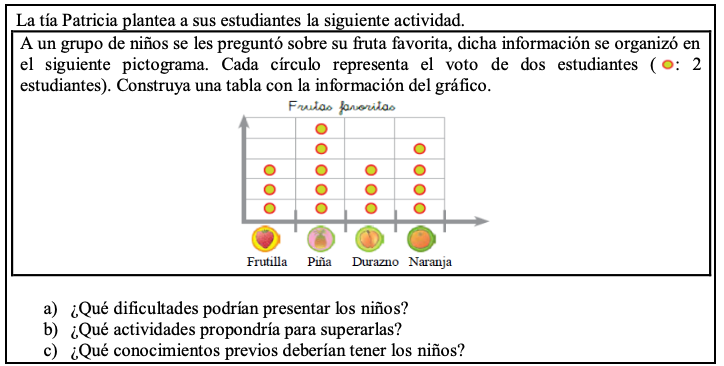
La puntuación de los expertos fluctúa entre 4,5 y 4,7 en claridad; entre 4,7 y 4,8 en pertinencia; y 4,8 en relevancia en cada pregunta del ítem. En el caso de la moda, en todos los aspectos se puntúa 5. Junto con estas puntuaciones, se consideran algunos comentarios que están en concordancia con nuestro objetivo y apuntan a la mejora del instrumento:

a) ¿Qué dificultades podrían presentar los niños PARA QUÉ?; b) ¿Qué actividades propondría para superarlas QUÉ?; c) ¿Qué conocimientos previos deberían tener los niños PARA QUÉ? (Experto 3).

En la 7b conviene preguntar por la justificación. Respecto de la enseñanza (y en relación con el horizonte), también propondría algún ítem con errores, para ver si los detectan y explican de dónde nacen (Experto 5).

Creo que la actividad debería estar contextualizada para una edad determinada de los niños, o las respuestas pueden ser demasiado amplias. ¿Hay algún análisis previo de las respuestas correctas que se esperan? ¿Un listado con las dificultades tipo? (Experto 6).

Entre los cambios realizados está el precisar un nivel educativo para los niños (kinder). Además, en la primera pregunta se agrega para construir la tabla; en la segunda se añade la pregunta ¿Por qué?, para que las futuras educadoras de párvulos tengan que justificar sus respuestas; en la tercera se agrega la expresión desarrollar la tarea.

4.8. Ítem 8

El octavo ítem (¿Qué importancia asigna usted a los gráficos estadísticos en la formación del futuro ciudadano?) tiene por propósito evaluar el conocimiento del horizonte matemático sobre gráficos estadísticos por futuras educadoras de párvulos. Este ítem, pese a su alta valoración en los criterios considerados (claridad, pertinencia y relevancia), es modificado para atender de mejor forma al tipo de conocimiento en cuestión. Los siguientes son los comentarios de expertos que permitieron la mejora del ítem:

Hay que tener claro que esto es preguntar por una creencia, no por un conocimiento, por lo tanto hay que reformularla, porque lo interesante es ver por qué es importante esto para el participante, que sepa conectarlo con usos o le dé valor por sí mismo. Así se da respuesta al indicador del conocimiento del horizonte. Por otro lado, el conocimiento del horizonte tiene una representación pobre en este estudio. Se pueden preguntar por conexiones con la probabilidad y por sesgos y dificultades (tanto probabilísticos como estadísticos) que se identifican más adelante (Experto 5).

La pregunta es demasiado amplia. En las respuestas quizá no se vea clara la importancia que las maestras pueden dar a la conexión de los gráficos estadísticos con otras áreas (Experto 6).

Se podría mejorar la relación con el horizonte matemático haciendo alguna referencia a qué situaciones o conceptos estadísticos debe conocer o desarrollar para ampliar su dominio en estadística (Experto 7).

En este artículo se han descrito los procesos de diseño y validación, por juicio de expertos, de un cuestionario para evaluar el conocimiento matemático para la enseñanza de los gráficos estadísticos en las futuras educadoras de párvulos en el contexto chileno. Con esto se aporta un instrumento con altas valoraciones sobre un tema y nivel formativo que son poco estudiados.

Ainley, J., Pratt, D. y Nardi, E. (2001). Normalising: children’s activity to construct meanings for trend.Educational Studies in Mathematics, 45(1-3), 131 – 146.

Alsina, A. (2012). La estadística y la probabilidad en Educación Infantil conocimientos disciplinares, didácticos y experienciales. Didácticas Específicas, 7, 4-22.

Alsina, A. y Vásquez, C. (2017). Hacia una enseñanza eficaz de la estadística y la probabilidad en las primeras edades. Didasc@lia: Didáctica y Educación, 8(4), 199-212.

Arteaga, P., Batanero, C., Cañadas, G. y Contreras, J. M. (2011). Las tablas y gráficos estadísticos como objetos culturales. Números, 76, 55-67.

Ball, D. L. (1990). Breaking with experience in learning to teach mathematics: the role of a preservice methods course. For the Learning of Mathematics, 10(2), 10-16.

Ball, D. L. y Bass, H. (2000). Interweaving content and pedagogy in teaching and learning to teach: Knowing and using mathematics. En J. Boaler (Ed.), Multiple perspectives on the teaching and learning of mathematics (pp. 83-104). Westport, CT: Ablex.

Ball, D. L., Lubienski, S. y Mewborn, D. S. (2001). Research on teaching mathematics: the unsolved problem of teachers’ mathematical knowledge. En V. Richardson (Ed.), Handbook of research on teaching (pp. 433-456). New York, NY: Macmillan.

Ball, D. L., Hill, H. C. y Bass, H. (2005). Knowing mathematics for teaching: Who knows mathematics well enough to teach third grade, and how can we decide? American Educator, 29(3), 14-17, 20-22, 43-46.

Ball, D., Thames, M. y Phelps, G. (2008). Content Knowledge for Teaching: what makes it special? Journal of Teacher Education, 59(5), 389-407.

Barraza, M. A. (2007). La consulta a expertos como estrategia para la recolección de evidencias de validez basadas en el contenido. Revista de Investigación Educativa Duranguense, 2(7), 5-14.

Carrillo, J., Climent, N., Contreras, L. C. y Muñoz-Catalán, M. C. (2013). Determining specialised knowledge for mathematics teaching. En B. Ubuz, C. Haser y M. Mariotti (Eds.), Proceedings of the CERME 8 (pp. 2985-2994). Antalya, Turquía: ERME.

Cavalcanti, M. R., Natrielli, K. R. Y Guimarães, G. (2010). Gráficos na mídia impressa. BOLEMA, 23(36), 733-751.

Cazorla, I. y Utsumi, M. C. (2010). Reflexões sobre o ensino de estatística na educação básica. En I. Cazorla y E. Santana (Eds.), Do tratamento da informação ao letramento estatístico (pp. 9-18). Itabuna: Via Litterarum.

Cervilla, C., Arteaga, P. y Díaz-Levicoy, D. (2014). ¿Es posible trabajar con gráficos estadísticos en preescolar? RECHIEM, 8(1), 33-38.

Ponte, J. P. y Chapman, O. (2008). Preservice mathematics teachers’ knowledge and development. En L. D. English (Ed.), Handbook of International Research in Mathematics Education (pp. 233 -261). New York, NY: Routledge.

Díaz-Levicoy, D. (2018). Comprensión de gráficos estadísticos por alumnos chilenos de Educación Primaria (Tesis Doctoral). Universidad de Granada, España.

Díaz-Levicoy, D., Batanero, C. Arteaga, P. y López-Martín M. M. (2015). Análisis de los gráficos estadísticos presentados en libros de texto de Educación Primaria chilena. Educação Matemática Pesquisa, 17(4), 715-739.

Díaz-Levicoy, D., Morales, R., Cruz, A. y López-Martín, M. M. (2016). Validación de un cuestionario para evaluar la comprensión sobre tablas estadísticas en Educación Primaria. Libro de actas del IV Congreso Internacional de Investigación e Innovación en Educación Infantil y Educación Primaria (pp. 518-524). Murcia: Universidad de Murcia.

Díaz-Levicoy, D., Sepúlveda, A., Vásquez, C. y Opazo, M. (2017). Organización de las respuestas sobre tablas estadísticas por futuras maestras de educación infantil desde la taxonomía SOLO. Didasc@lia: Didáctica y Educación, 8(2), 193-212.

English, L. D.  y Watson, J. M. (2015). Statistical literacy in the elementary school: Opportunities for problem posing. En F. Singer, N. Ellerton y J. Cai (Eds.), Mathematical problem posing: from research to effective practice (pp. 241-256). New York, NY: Springer.

Escobar-Pérez, J. y Cuervo-Martínez, A. (2008). Validez de contenido y juicio de expertos: una aproximación a su utilización. Avances en Medición, 6(1), 27-36.

Gal, I. (2002). Adult´s statistical literacy: Meaning, components, responsibilities. International Statistical Review, 70(1), 1-25.

Godino, J. D. (2009). Categorías de análisis de los conocimientos del profesor de matemáticas. UNIÓN, 20, 13-31.

Gómez, P. (2007). Desarrollo del conocimiento didáctico en un plan de formación inicial de profesores de matemáticas de secundaria (Tesis Doctoral). Universidad de Granada, España.

Hill, H. C. y Ball, D. L. (2004). Learning mathematics for teaching: Results from California's mathematics professional development institutes. Journal for Research in Mathematics Education, 35(5), 330-351.

Hill, H. C., Ball, D. L. y Schlling, S. G. (2008). Unpacking pedagogical content knowledge of students. Journal for Research in Mathematics Education, 39(4), 372-400.

Hill, H. C., Rowan, B. y Ball, D. L. (2005). Effects of teachers’ mathematical knowledge for teaching on student achievement. American Educational Research Journal, 42(2), 371-406.

Lopes, C. A. E. (2004). Literacia estatística e o INAF 2002. En M. Fonseca, (Ed.), Letramento no Brasil: habilidades matemáticas (pp. 187-197). São Paulo: Global.

MEC (1997). Parâmetros Curriculares Nacionais: Matemática, Ensino de 1a à 4a série. Brasília: Secretaria de Educação Fundamental.

MEC (2017). Base Nacional Comum Curricular. Brasília: Secretaria de Educação Básica.

MECD (2014). Real Decreto 126/2014, de 28 de febrero, por el que se establece el currículo básico de la Educación Primaria. Madrid: Ministerio de Educación, Cultura y Deporte.

Millman, J. y Greene, J. (1989). The specification and development of tests of achievement and ability. En R. Linn (Ed.), Educational measurement (p p. 335-366). Londres: Macmillan.

MINEDU (2009). Diseño Curricular Nacional de Educación Básica Regular. Lima: DIGEBR.

MINEDU (2016). Programa curricular de Educación Primaria. Lima: Ministerio de Educación.

MINEDUC (2012). Matemática educación básica. Bases curriculares. Santiago: Unidad de Currículum y Evaluación.

Pino-Fan, L. y Godino, J. D. (2015). Perspectiva ampliada del conocimiento didáctico-matemático del profesor. Paradigma, 36(1), 87-109.

Sepúlveda, A., Díaz-Levicoy, D. y Jara, D. (2018). Evaluación de la comprensión sobre Tablas Estadísticas en estudiantes de Educación Primaria. BOLEMA, 32(62), 869-886.

Shulman, L. S. (1986). Those who understand: Knowledge growth in teaching. Educational researcher, 15(2), 4-14.

Shulman, L. (1987). Knowledge and teaching: Foundations of the new reform. Harvard educational review, 57(1), 1-23.

Skjong, R. y Wentworth, B. H. (2001). Expert judgement and risk perception. ISOPE. Offshore and polar engineering conference, 4, 537–544.

Varas, L., Lacourly, N., López, A. y Giaconi, V. (2013). Evaluación del conocimiento pedagógico del contenido para enseñar matemáticas elementales. Enseñanza de las Ciencias, 31(1), 0171-187.

Vásquez, C. y Alsina, A. (2019). Intuitive ideas about chance and probability in children from 4 to 6 years old. Acta Scientiae, 21(3), 131-154.

Vásquez, C., Díaz-Levicoy, D., Coronata, C. y Alsina, Á. (2018). Alfabetización estadística y probabilística: primeros pasos para su desarrollo desde la Educación Infantil. Cadernos Cenpec, 8(1), 154-179.

Watson, J. M. (2013). Statistical literacy at school: growth and goals. Mahwah, NJ: Lawrence Erlbaum.

Estimados estudiantes, el siguiente instrumento tiene por objetivo identificar los conocimientos y habilidades de comprensión sobre gráficos. Agracemos, desde ya, su colaboración al responder estas preguntas. La información que se recogerá es exclusivamente con propósitos investigativos para, posteriormente, hacer propuestas de mejora en la formación docente. Además, los datos entregados por ustedes son anónimos.

Semestre que cursa  en la carrera:___________ Edad (años): _________ Sexo:___________

Ítem 1. ¿Cómo definiría usted un gráfico estadístico?

Ítem 2. Haga una lista considerando los conocimientos matemáticos y estadísticos que usa cuando trabaja con un gráfico de barras.

Ítem 3. De las siguientes tareas, sobre construcción de gráficos estadísticos, ¿Con cuál comenzaría usted la introducción a los gráficos estadísticos desde la Educación Infantil? Explique

Tarea 1

A los estudiantes se les preguntó por su fruta preferida, y los resultados se organizaron en la siguiente tabla. A partir de ella, construya un gráfico estadístico.

Tarea 2

A continuación, se muestran los resultados de una encuesta realizada por una profesora, en un curso de kínder. La pregunta formulada fue ¿cuántas mascotas tienes?

0, 1, 3, 2, 2, 3, 2, 4, 1, 2, 1, 2, 0, 2, 3, 1, 1, 0, 2, 4, 0, 1, 2, 3, 1, 1, 2, 2, 2

Realiza un gráfico de barras con los datos proporcionados.

Ítem 4. En el siguiente gráfico se muestra el nivel de aprobación y reprobación (en porcentaje: %) del desempeño de la directora del jardín infantil “Caracolito” durante los últimos nueve meses.

De acuerdo con la información mostrada en el gráfico, responda las siguientes preguntas.

1. Indique el tipo de gráfico.
2. ¿Qué porcentaje de desaprobación alcanzó la directora del jardín infantil en el Mes 5?
3. ¿Se observa algún tipo de tendencia en relación al nivel de aprobación y reprobación de la directora del jardín infantil? Explique brevemente.
4. ¿Cuál es el promedio de aprobación de la gestión durante los nueve meses?
5. ¿Cuál será el porcentaje de aprobación que tendría la directora del Jardín en el décimo mes? Explique cómo lo obtuvo.

Ítem 5. Una educadora dio a los niños de kínder la tarea de preguntar a los miembros de su familia sobre sus insectos favoritos. Las respuestas de uno de los niños se muestran en el siguiente diagrama.

Fuente: @pbeltranp

1. ¿Es correcta la representación realiza por el niño? Explique
2. ¿Cuál sería el grado de dificultad de esta tarea para los niños? Puntúe entre 1 y 5, donde 1 es muy fácil y 5 es muy difícil. Justifique.
3. ¿Qué gráfico estadístico usarías para representar esta información?

Ítem 6. Proponga un objetivo de aprendizaje para la enseñanza de los gráficos estadísticos en Educación Parvularia.

Ítem 7. La tía Patricia plantea a sus estudiantes la siguiente actividad.

1. ¿Qué dificultades podrían presentar los niños para construir la tabla?
2. ¿Qué actividades propondría para superarlas? ¿Por qué?
3. ¿Qué conocimientos previos deberían tener los niños desarrollar la tarea?

Ítem 8. ¿Con qué otros conocimientos matemáticos relaciona los gráficos estadísticos?

1. Doctora en Educación. Académica de la Facultad de Educación, Universidad Católica del Maule. E-mail: msamuel@ucm.cl

2. Doctor en Ciencias de la Educación.  Académico de la Facultad de Ciencias Básicas, Universidad Católica del Maule. E-mail: dddiaz01@hotmail.com

3. Doctor en Educación. Académico de la Facultad de Educación y Humanidades, Universidad del Bío-Bío. E-mail: frodriguez@ubiobio.cl