ISSN 0798 1015

Vol. 40 (Issue 40) Year 2019. Page 19

Multicriteria optimization model of the interaction of elements when managing network integrated structures

Modelo de criterios múltiples de optimización de las interacciones de elementos al gestionar estructuras integradas de red

PROSVIRKIN, Nikolai 1; BLINOVA, Ekaterina 2 & GERASIMOV, Kirill 3

Received: 03/08/2019 • Approved: 11/11/2019 • Published 18/11/2019

Contents

1. Introduction

2. Methodology

3. Results

4. Conclusions

Bibliographic references

1. Introduction

In practice, there are several basic organizational options for inter-company interactions. A variety of options for enterprises’ linking varies from almost complete freedom to full integration with loss of independence. The choice of a particular type of partnership is determined by the conditions in which companies operate. Integrated structures can be divided into two main types: vertically and horizontally integrated structures (Geraskin, 2017). Regardless of the nature of the interaction, a number of common problems arise, as follows:

– each participant seeks to get the greatest profit;

– coordination of interests must be carried out at different levels;

– interaction is carried out in conditions of limited information.

Managing the interactions of companies in network structures is a complicated and knowledge-intensive process. The management requires knowledge in various fields of science (Berrah et al, 2011). We analyzed the publications of various areas related to the management of interactions of elements in network structures.

In recent decades, the material flows management was studied by Russia authors: Gadzhinsky, 2006; Anikin et al., 2006; Ryzhikov, 1969; Sterligova, 2004.

The scientific substantiation of the methods for organizational systems managing (such as contract theory, operations research, the theory of active systems, etc.) is represented in works of Germeyer, 1976; Gorelik et al., 1999; Burkov et al., 1994; Kukushkin et al., 1984; Nash et al., 2016; Aumann et al., 1988; Moulin, 1991.

The development of vector optimization and graph theory methods is presented in the works of Mashunin, 1986; Harary, 1969.

The development of solutions to multicriteria problems is presented in the works of Shikin et al., 2006; Steuer, 1986.

An analysis of publications shows that scientists have substantiated the basic principles of product management, developed many models of inventory management, but not all aspects of interaction management have been thoroughly studied and developed from a practical point of view.

It should be noted that the specific features of the interaction of companies in integrated network structures, such as the need to ensure cost reduction while reducing the delivery time of products and increasing the workload of warehousing and transport, have not yet been reflected. This circumstance determined the relevance and expediency of choosing this topic as a subject of study.

The aim of the study is to increase the efficiency of companies integrated into network structures by developing an interaction optimization model for integrated companies. Achieving this goal identified the following objectives of this research.

1. Definition of interrelated criteria for optimizing the interactions of companies integrated into network structures, which will allow to quantify the costs of product distribution, delivery times, as well as the workload of equipment, warehousing and transport.

2. Development of a multi-criteria interaction optimization model for integrated companies focused on system management methods that simultaneously takes into account the costs of product distribution, delivery times, traffic of vehicles and equipment.

The object of the research is the relations arising in the process of business and interaction of companies integrated into network structures.

The subject of the study are models that ensure the organization of effective work of integrated network structures. Information base of the research is the materials published on the research topic in the scientific, periodical and special literature.

Chapter 1 text

Usually, when modeling interactions in integrated structures, many modern studies do not take into account the multifactorial nature of relationships. In our opinion, the lack of consideration of multi-criteria in theory leads to erroneous conclusions, and in practice – to the loss of profits. Therefore, to increase the efficiency of business, it is necessary to consider separately each type and form of interaction in order to establish an exhaustive number of criteria (Currarini et al, 2016).

The scientific novelty of the research is as follows.

1. Criteria for optimizing the interaction of integrated companies into network structures have been formed, which allow quantifying the distribution costs, delivery times and workload of warehousing and transport.

2. A multi-criteria model of optimization of interactions of integrated companies into network structures based on established criteria has been developed, which makes it possible to fully take into account the costs of product flow, delivery times and workload of warehousing and transport at the same time.

In the general case, when interacting elements within a single technological process, as well as when moving products along distribution channels, the following main criteria should be considered.

1. Reducing the cost of product distribution.

2. Reducing time spent on product delivery.

3. Accounting for the loading of warehousing and transport.

The article proposed a multi-criteria model that takes into account the above criteria. Vertical integration is considered without joining any alliances, etc. The interaction begins only under the condition that it is beneficial to the final part - the trading company. In practice, the individual parts of the distribution network have their own interests, but they were not taken into account in the criteria or restrictions, since the movement of a through material flow was considered. The movement of the material flow along the parts of the chain should be optimal from the point of view of the final part.

The question of whether the parts are independent economic entities remains outside the scope of the model, since the form of ownership does not matter for the model (Ivanov et al, 2018).

There are several possible suppliers on the market for a trading company (or an assembly plant) that can supply a resource (goods, products, components) of several product groups A = {1,…, a,… m}, where a is a serial number of the nomenclature product group. N = {1,…i, j…n} is the number of elements (workshop, production, agents, warehouses, etc.) that can participate in the interaction. Every production company i N can produce a resource in volume of 0 ≤ wi ≤ Wi and sell the goods to another company j N, j ≠ i in volume 0 ≤ vij ≤ Vij.

There may be a large number of suppliers for the existing trading structure. The same company can act as both a buyer and a seller.

It is required to construct a scheme for the interaction X of production and trade elements for the optimal movement of goods from producers to consumers, if the agreed supply volume is vs, purchase price of the product item from the manufacturer is Pai, the number of items ordered by the trading structure for one delivery  is Qa, number of working days per year is Tr.

The interaction of elements (Burkov et al., 2015; Geraskin, 2005) is represented as an oriented graph (Zykova, 1987), consisting of N elements (see fig. 1 and 2).

Figure 1
Real interaction scheme

-----

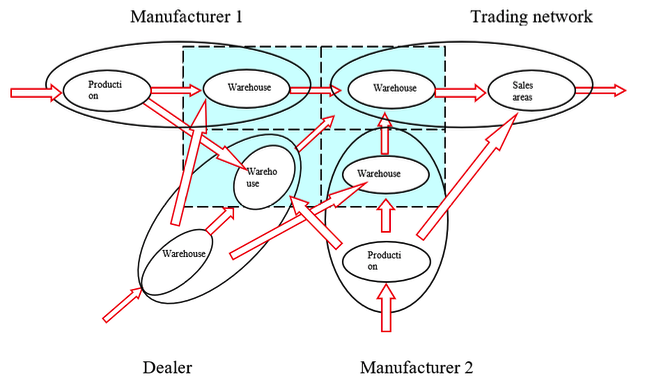
Figure 2
Formal interaction system

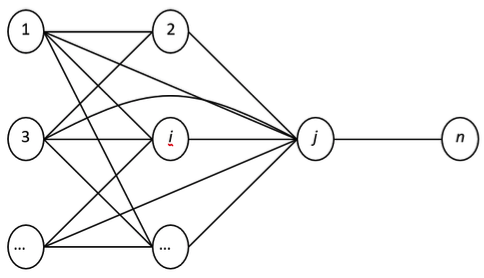
The company possesses the retrospective information about the values of demand in the market for previous periods vt. Basing on information on the market volume, the trading company determines the required volume of deliveries vs, which is subsequently subject to sale.

We introduce the following notation.

In this case, transportation and procurement costs and storage costs are denoted equally as types of costs. However, along the diagonal of the matrix, storage costs are postponed for the period, while the remaining matrix elements reflect transportation and procurement costs. Costs are calculated on the basis of cost estimates and, in turn, consist of a number of items. Transportation and procurement costs are expenses for a certain period (for which i orders are made), they are not necessarily related to one order. They have to be lead to the same order.

Estimated transportation and procurement costs (per order) includes the following types of costs:

The formulation of performance criteria and a system of constraints makes it possible to approach the formulation of the problem of forming an interaction scheme, which consists in the following. It is required to construct a matrix of a directed graph X representing the product supply structure, which contains n vertices interconnected so that the selected efficiency criteria reach optimal values taking into account the constraints. The search for optimal interaction is carried out using the principles of solving multicriteria problems (Geraskin, 2017). The criteria of the task are heterogeneous, as part of the optimization criteria tends to the minimum value, and one to the maximum. The method of optimizing the supply chain and product distribution involves the choice of supply chain based on the Pareto-optimal controls (Nogin et al, 1982). The above optimization criteria are in significant economic contradiction, since with a reduction in the time of delivery of goods from producer to consumer, transport and procurement costs and costs associated with storage increase. Transportation and procurement costs of system elements increase with shorter delivery times, since in this case it is necessary to use more mobile vehicles for cargo delivery g4, the associated costs increase significantly g1, g2, g3. The cost of storing cargo also increases, due primarily to the need to maintain large quantities of products in warehouses r1, r2, r3. In addition, each element of the system is interested in increasing load factors. However, as load factors increase, product delivery time increases.

The complexity of the problems and the inconsistency of the criteria led to the emergence of a number of mathematical models that can adequately reflect the stated problem and its multi-purpose nature (Gorodnov et al., 2005; Burkov et al, 2013). There are a number of methods for solving multicriteria problems described in (Shikin et al., 2006). The main ones include the assignment method, the ideal point method, the folding method, the constraint method, the hierarchy analysis method. These methods are general, and it is necessary to select and adapt a specific method for solving the stated problem. In solving the formulated problem, in the author’s opinion, it is advisable to use multi-criteria optimization models. In this case, the question arises about the choice of a complex optimality criterion, which includes all three criteria. We formulate the problem of vector interaction optimization in general.

4. Conclusions

Analysis of the proposed model allows us to draw several conclusions. First, the model has a network nature of the interaction of elements and leads to a class of multicriteria vector optimization problems. Secondly, when forming the optimal interaction, it is advisable to use methods based on the choice of a compromise solution. Thirdly, the formation of the system takes place under conditions of limited delivery times, volumes of deliveries while simultaneously fulfilling the requirements for a minimum economic effect, the minimum required number of connections between the elements and the maximum loading of equipment, warehousing and transport. And finally, the solution to the compromise task of finding the optimal interaction is to find such a number of connections between the elements of the system and their mutual arrangement, in which the system is the least expensive in terms of costs and delivery time and most loaded in the use of equipment, storage and transport.

1. Anikin, B.A. & Tyapukhin, A.P. (2006). Commercial logistics. Мoscow. Prospect Publ.

2. Aumann, R. & Myerson, R. (1988). Endogenous Formation of Links Between Players and Coalitions: An Application of the Shapley Value. Cambridge University Press.

3. Berrah, L., Montmain, J., Mauris, G. & Clivillé, V. (2011). Optimising industrial performance improvement within a quantitative multi-criteria aggregation framework. International Journal of Data Analysis Techniques and Strategies, 3(1), pp. 42-65.

4. Burkov, V.N., Novikov, D.A. & Shchepkin, A.V. (2015). Control mechanisms at the level of industrial enterprises. Studies in Systems, Decision and Control. 10, pp. 25-70.

5. Burkov, V.N., Goubko, M.V., Korgin, N.A. & Novikov, D.A. (2013). Integrated mechanisms of organizational behavior control. Advances in Systems Science and Applications. 13(3), pp. 218-226.

6. Burkov, V.N. & Enaleev, A.K. (1994). Stimulation and decision-making in the active system theory. Review of problems and new results. Mathematical Social Sciences. 27(3), pp. 271-291.

7. Currarini, S., Marchiori, C. & Tavoni, A. (2016). Network Economics and the Environment: Insights and Perspectives. Environmental and Resource Economics. 65(1), pp. 159-189.

8. Gadzhinsky, A.M. (2006). Logistics. Moscow. Dashkov and Co Publ.

9. Geraskin, M. (2017). Game-theoretic analysis of Stackelberg oligopoly with arbitrary rank reflexive behavior of agents. Kybernetes. 46(6), pp. 1052-1067.

10. Geraskin, M. (2005). Coordination of economic interests in structures of corporations. Moscow. ICS RAS, Anko Publ.

11. Germeyer, Yu.B. (1976). Games with Opposite Interests. Moscow. Nauka Publ.

12. Gorelik, V.A. & Fomina, T.P. (1999). Game Theory Elements. Lipetsk: LGYU Publ.

13. Gorodnov, V.P. & Fyk, O.V. (2005). Mathematical modeling, performance evaluation and synthesis of organizational structures of enterprises. Kharkov. NUA Publ.

14. Harary, F. (1969). Graph theory. Addison-Wesley.

15. Ivanov, D., Belyaeva, E., Kurilova, A. & Popkova, E. (2018). Models for the interaction between space services providers and manufacturers of space vehicles. Entrepreneurship and Sustainability Issues. 5(4), pp. 846-857.

16. Kukushkin, N.S. & Morozov, V.V. (1984). Theory of non-antagonistic games. Moscow. MSU Publ.

17. Mashunin Yu.K. (1986). Methods and models of vector optimization. Moscow. Nauka Publ.

18. Moulin, H. (1991). Axioms of Cooperative Decision Making, Cambridge University Press.

19. Nash, J.F. & Rassias, M.Th. (2016). Open Problems in Mathematics. Springer International Publishing Switzerland.

20. Nogin, V.D. & Podzhovsky, V.V. (1982). Pareto-optimal solutions to multicriteria problems. Moscow. Nauka Publ.

21. Ryzhikov, Yu. (1969). Inventory Management. Мoscow. Nauka Publ.

22. Shikin, E.V. & Shikina, E.V. (2006). Operations research. Moscow. Prospect Publ.

23. Sterligova, A.N. (2004). Logistic terminology structure. Logistics and Supply Chain Management. 4-5, pp. 101-119.

24. Steuer, R.E. (1986). Multiple criteria optimization; theory, computation, and application. Wiley.

25. Zykova, А.А. (1987). Graph theory basics. Moscow. Nauka Publ.

1. Department of Management, Samara National Research University, Samara, Russian Federation; Contact e-mail: nik-prosvirkin@ssau.ru

2. Department of Mathematical Methods in Economics, Samara National Research University, Samara, Russian Federation; Contact e-mail: blinova@ssau.ru

3. Department of Economics, Samara National Research University, Samara, Russian Federation; Contact e-mail: kgerasimov@ssau.ru