

Vol. 40 (Nº 38) Año 2019. Pág. 18
GARCIA, Fernando 1; GONZÁLEZ-BUENO, Jairo 2; OLIVER, Javier 3 y RUEDA-BARRIOS, Gladys 4
Recibido: 07/05/2019 • Aprobado: 30/10/2019 • Publicado 04/11/2019
2. Medidas de riesgo en la selección de carteras
RESUMEN: La esencia del problema de selección de cartera es encontrar las proporciones óptimas del capital que ha de invertir en cada activo buscando un equilibrio entre la maximización del rendimiento y la minimización del riesgo de la inversión. En atención a lo anteriormente expuesto, este articulo presentará un análisis comparativo de las medidas de riesgo utilizadas en los modelos de optimización de carteras. |
ABSTRACT: The essence of the portfolio selection problem is to determine the optimal amount of capital to invest in each asset, and seeking a balance between maximizing returns and minimizing risk. Based on the above statement, this paper analyses the risk measures used in portfolio optimization models. |
La toma de decisiones multicriterio incluye un grupo de métodos de investigación operativa que persiguen la toma de decisiones en presencia de múltiples criterios, metas u objetivos. Este tipo de método se apartan de los métodos tradicionales de investigación operativa basados en un único objetivo y tienen por objeto apoyar a los decisores en la optimización simultánea de varios objetivos que generalmente presentan conflictos entre sí (Ballestero, Pérez-Gladish, y Garcia-Bernabeu, 2015). Las decisiones multicriterio han sido aplicadas en numerosos ámbitos (Arribas, García, Guijarro, Olive, y Tamošiūnienė, 2016; Boza Valle, Manjarrez Fuentes, y Vega De La Cruz, 2018; Dassan, Santos, Da Silva, Kawamoto, y Rodrigues, 2016) y el de las inversiones financiaras no es una excepción (García, González-Bueno, Oliver, y Tamošiūnienė, 2019; García, Guijarro, y Moya, 2013; García, Guijarro, Oliver, y Tamošiūnienė, 2018; Masood, Tvaronavičienė, y Javaria, 2019; Xidonas, Doukas, Mavrotas, y Pechak, 2016).
Un ejemplo característico en la toma de decisiones multicriterio es el problema de optimización de carteras. Desde el punto de vista financiero, una cartera es un grupo de títulos o de otras inversiones, creado comúnmente para lograr una o más metas de inversión (Gitman y Joehnk, 2009). En los mercados de valores existe una gran variedad de activos en los cuales un inversionista puede invertir su riqueza. Sin embargo, estos activos poseen diferentes niveles de riesgo e, igualmente, los inversionistas poseen sus propias preferencias y actitudes frente el riesgo. Dado un conjunto de N activos con diferentes características, la esencia del problema de selección de cartera es encontrar las proporciones óptimas del capital que ha de invertir en cada activo buscando un equilibrio entre la maximización del rendimiento y la minimización del riesgo de la inversión (Bermúdez y Vercher, 2012). El primer trabajo novedoso sobre este tema fue el modelo de cartera de media-varianza propuesto por Markowitz (1952), quien asumió el rendimiento de cada activo como una variable aleatoria y el riesgo de la inversión como la varianza de los rendimientos de la cartera (Vercher y Bermúdez, 2015). Desde la propuesta de Markowitz, la teoría de selección de cartera se ha desarrollado y se ha extendido para resolver algunos inconvenientes del modelo original (Ponsich, Jaimes, y Coello, 2013). La mayor parte de las investigaciones han abordado problemas como la medición del rendimiento y el riesgo, la introducción de nuevos criterios y restricciones realistas, y la selección de carteras especificas a lo largo de la frontera eficiente (F. García et al., 2019).
Sobre la base de las consideraciones anteriores, este articulo tiene como pretensión realizar una revisión sistemática de la literatura que permita analizar no solo el modelo clásico de media-varianza, sino también revisar varias extensiones de este modelo considerando medidas alternativas para cuantificar el riesgo.
El articulo está organizado de la siguiente manera: La sección 2 abordará un análisis de las medidas de riesgo de dispersión y las medidas de riesgo downside utilizadas en los modelos de optimización de carteras, y la sección 3 presentará las conclusiones correspondientes a esta investigación.
El concepto de riesgo no tiene una definición universalmente aceptada, ya que éste varía no solo según el campo de aplicación, sino también según la situación. No obstante, la mayoría de las definiciones de riesgo comparten dos elementos comunes. El primer elemento es la posibilidad de un resultado indeseable que se desvía de lo que se espera. El segundo elemento es una incertidumbre básica asociada a la ocurrencia de este resultado indeseable. Sí esta incertidumbre se puede cuantificar en términos de las evaluaciones de probabilidad, entonces se dice que la situación de riesgo es calculable. Sí, además, estas evaluaciones de probabilidad se interpretan como evaluaciones objetivas (i.e., independientemente de las creencias humanas), se dice que el riesgo es objetivo; de lo contrario se dice que es subjetivo (Nanpeng Yu, Somani, y Tesfatsion, 2010).
Figura 1
Tipos de Riesgos Financieros

Fuente: Elaboración propia a partir de McNeil et al. (2005) y, Unger y Poddig (2014)
En finanzas, el riesgo se define como “la incertidumbre asociada con el valor y/o retorno de una posición financiera” (Montoya, Rave, y Castaño, 2006, p. 275). Usualmente, según su naturaleza los riesgos financieros se clasifican en: riesgo de mercado, riesgo de crédito, riesgo de operación y riesgo de liquidez (McNeil, Frey, y Embrechts, 2005; Unger y Poddig, 2014) tal y como se muestra en la figura 1. Además, Dowd (2002) subraya que el riesgo de mercado se subdivide en otros tipos más específicos de riesgo, como por ejemplo, riesgo del subyacente, riesgo de tasas de interés, riesgo de tipo de cambio, riesgo asociado al precio de los commodities, entre otros. A este respecto, este articulo cubre el aspecto relacionado con el riesgo de mercado, esto es, el riesgo derivado de la variación en los precios de mercado de los activos en una cartera dada.
Sobre la base de las consideraciones anteriores, en el problema de selección de cartera se distinguen dos tipos de medidas de riesgo: medidas de riesgo de dispersión y medidas de riesgo downside (Fabozzi, Kolm, Pachamanova, y Focardi, 2007; Ortobelli, Rachev, Stoyanov, Fabozzi, y Biglova, 2005). A continuación, se expone un análisis comparativo de las medidas de riesgo mencionadas y su uso en problema de selección de carteras.
Estas medidas de riesgo, denominadas también como “simétricas”, penalizan los rendimientos tanto por encima como por debajo del rendimiento esperado; es decir, no hacen distinción entre las desviaciones positivas (i.e. ganancias) y desviaciones negativas (i.e. perdidas) respecto al valor esperado del rendimiento (Fabozzi, Focardi, y Kolm, 2010). A continuación, se analizarán las medidas de riesgo simétricas de varianza y desviación absoluta.
El paso más importante en la dirección de la gestión cuantitativa de carteras fue realizado por Markowitz (1952) con la introducción del modelo de optimización de cartera basado en un contexto bi-criterio de riesgo-retorno (media-varianza). Esta teoría popularmente referida como teoría moderna de portafolio, proporciono una respuesta a la pregunta fundamental: ¿Cómo debería un inversionista asignar el capital entre las posibles opciones de inversión? En este orden de ideas, el análisis de cartera se debe fundamentar en algunos criterios que sirvan de guía para lo importante y lo poco importante, lo relevante y lo irrelevante (Azmi, 2013). La elección adecuada de estos criterios depende de la situación y la naturaleza del inversionista. No obstante, hay dos criterios que son comunes a todos los inversionistas: la media (retorno esperado) y la varianza del retorno (riesgo). Para Markowitz, las “creencias” o proyecciones respecto a los activos, siguen las mismas reglas de probabilidad que obedecen a las variables aleatorias. Bajo esta suposición, se deduce que el rendimiento esperado de la cartera, es el promedio ponderado de los rendimientos esperados de los activos individuales, y la varianza del rendimiento de la cartera es una función particular de las varianzas de, y las covarianzas entre, los activos y sus pesos en la cartera (Gupta, Mehlawat, Inuiguchi, y Chandra, 2014). Por lo tanto, los inversionistas deben considerar de forma conjunta el riesgo y el retorno, y determinar la asignación de capital entre las alternativas de inversión sobre la base del principio trade-off entre ellos (Kolm, Tütüncü, y Fabozzi, 2014). Además, Markowitz sugirió que la selección de carteras debe basarse en las creencias razonables sobre el desempeño futuro más que el desempeño pasado per se. Las percepciones basadas en los desempeños pasados asumen, en efecto, que el promedio de los retornos en el pasado son buenas estimaciones del retorno “probable” en el futuro, y la varianza del retorno en el pasado es una buena medida de la incertidumbre del retorno en el futuro (Gupta et al., 2014). A continuación se presentará la formulación matemática del modelo de media varianza propuesto por Markowitz (1952):
El rendimiento de un activo se expresa como la tasa de rendimiento, que se define durante un período dado como:

Así mismo, es importante señalar que bajo el contexto de este modelo un inversionista preferirá tener una cartera que ofrezca el mayor retorno esperado posible y además que la rentabilidad de ésta tenga la mínima dispersión o variabilidad posible. Con este propósito, Markowitz sugirió que la varianza que mide la dispersión del rendimiento esperado, podría ser utilizada para cuantificar el riesgo de la cartera. En este orden de ideas, la varianza del rendimiento esperado de una cartera estará dada por (Gupta et al., 2014, p. 4):
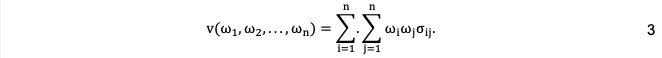
Prosiguiendo con el análisis del modelo de media varianza, es importante señalar que el cálculo del riesgo como la varianza de los rendimientos de los activos ha generado varias críticas entre los investigadores y académicos (Artzner, Delbaen, Eber, y Heath, 1999; Fabozzi et al., 2007; Metaxiotis y Liagkouras, 2012; Vercher y Bermúdez, 2012), las cuales se relacionan a continuación (Gupta et al., 2014):
i) El supuesto de una distribución normal multivariante de la tasa de rendimiento de los activos no se mantiene en la práctica (las distribuciones son típicamente asimétricas).
ii) Los problemas de programación cuadrática de gran escala son difíciles de resolver (complejidad computacional).
iii) Para los mercados reales, el tamaño de la matriz de varianza-covarianza puede ser muy grande y, por lo tanto, difícil de estimar.
Varios autores trataron de aliviar estas dificultades utilizando diversos esquemas de aproximación. El modelo de índice único de Sharpe (1963) es un avance en esta dirección. Este autor señaló que, si el problema de la selección de la cartera pudiera formularse como un problema de programación lineal, las perspectivas de las aplicaciones prácticas serían mejoradas. Como resultado de esto, en las últimas décadas se han hecho varios intentos para linealizar el modelo de optimización de cartera utilizando medidas alternativas de riesgo que serán analizadas en las siguientes secciones.
El modelo de optimización de carteras de desviación media absoluta fue introducido por Konno (1988, 1990) y, posteriormente refinado por Konno y Yamazaki (1991), como una alternativa al modelo de optimización de carteras de media varianza de Markowitz. Para los autores la desviación absoluta de una variable aleatoria es el valor absoluto esperado de la diferencia entre la variable aleatoria y su media. A este respecto, el riesgo de la cartera medido como desviación absoluta se expresa como (Gupta et al., 2014, p.21):

Konno y Yamazaki (1991) presentaron un teorema y probaron la equivalencia del modelo de media varianza y de desviación media absoluta, en un entorno en el cual la distribución conjunta de los rendimientos de los activos se asume como normal multivariante. Los resultados obtenidos en el modelo de desviación media absoluta, en el que solo se necesita estimar los retornos esperados de los activos, provee resultados similares a los proporcionados en el modelo de media varianza, aunque en la práctica se obtienen carteras óptimas diferentes (Vercher, 2015). Esto obedece al hecho de que cada uno de los modelos utiliza diferentes estadísticos para estimar los parámetros de entrada del problema de optimización (Simaan, 1997). No obstante, ni el modelo de media varianza ni el modelo de desviación media absoluta es superior al otro desde el punto de vista de la estabilidad y rendimiento esperado de la inversión (Vercher, 2015, p. 26).
Prosiguiendo el análisis, es conveniente señalar que diversos estudios muestran que “los inversores o gestores de carteras asocian el riesgo a la variabilidad de los resultados negativos o pérdidas (downside risk) y no tanto a la de sus ganancias (upside potential)” (Manzana, 2009, p. 161). En otras palabras, los inversionistas o gestores de carteras se preocupan más por evitar las pérdidas que por buscar ganancias. Esta asimetría entre los resultados positivos y negativos respecto del valor esperado del rendimiento pone de manifiesto que tanto la varianza como la desviación absoluta no son medidas adecuada para cuantificar el riesgo, al menos tal y como es percibido por los inversionistas. Como se verá a continuación, varias medias de riesgo de tipo downside han sido propuestas en las últimas décadas para resolver este conflicto.
El objetivo de las medidas de riesgo downside en los modelos de optimización de carteras es maximizar la probabilidad de que el rendimiento esperado de la cartera esté por encima de cierto nivel mínimo aceptable (a menudo denominado nivel de referencia o nivel de desastre) (Fabozzi, Focardi, y Kolm, 2006). La ubicación del riesgo downside en una distribución hipotética del retorno de un activo se muestra figura 2. Como se puede apreciar, estas medidas de riesgo hacen una clara distinción entre las volatilidades de pérdidas (downside) y las volatilidades de ganancias (upside), y solo la volatilidad que se encuentra por debajo del nivel mínimo aceptado incurre en riesgo. En otras palabras, todas las rentabilidades por encima de este nivel de referencia generan "incertidumbre”, que no es más que una oportunidad sin riesgos para rendimientos inesperadamente altos (Rom y Ferguson, 1994). Nótese que frecuentemente las medidas de riesgo downside son computacionalmente más complicadas de usar bajo el contexto de la teoría de selección de carteras, debido a que con frecuencia se tiene que recurrir a estimaciones no paramétricas, a simulaciones y a técnicas de optimización computacionalmente intensivas (Fabozzi et al., 2010). Por otro lado, para la estimación de las medidas de riesgo downside solo se utiliza una porción de los datos originales, incluso solo la cola de la distribución empírica, ocasionando un aumento en el error de estimación. No obstante, estas medidas de riesgo son muy útiles para evaluar el riesgo de los activos financieros con distribuciones de retorno asimétricas, como por ejemplo las opciones de compra y venta y otros contratos de derivados (Fabozzi et al., 2007). A continuación, se analizarán las medidas de riesgo downside más comunes en el problema de selección de cartera.
Figura 2
Riesgo Downside
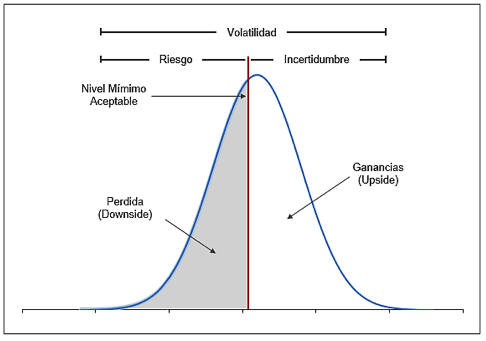
Fuente: Rom y Ferguson (1994)
Roy (1952) a través de su principio comportamental de “primero la seguridad”, proporcionó el primer paso hacia el modelo más completo de lo que la literatura financiera contemporánea denominada como teoría conductual de la cartera (Shefrin y Statman, 2000, citado en Chen, 2016). Este principio afirma que “la riqueza de las personas se encuentra constantemente expuesta a situaciones externas adversas, por lo cual es lógico que ellas, influidas por el miedo y la necesidad de seguridad, traten de reducir la probabilidad de ocurrencia de una catástrofe financiera”(Useche-Arévalo, 2015). En la teoría clásica de cartera, un inversionista construye una cartera bajo el principio de trade-off riesgo-retorno. El trade-off entre el riesgo y el retorno, y la asignación de los activos de la cartera, dependen de la función de utilidad del inversionista. Bajo este contexto, puede ser difícil, o incluso imposible, determinar la función de utilidad real de un inversionista (Fabozzi et al., 2006). Ahora bien, bajo el enfoque de “primero la seguridad”, un inversor en lugar de pensar en términos de la función de utilidad, primero debe asegurarse conservar una cierta cantidad de capital (Fabozzi et al., 2010). A partir de entonces decide el retorno mínimo aceptable que logre la preservación de este capital. En esencia, el inversor elige su cartera resolviendo el siguiente problema de optimización (Chapados, 2011):

Markowitz (1959) propuso el uso de la semivarianza para corregir el hecho de que la varianza penaliza por igual las rentabilidades positivas y negativas. Años más tarde reconoció que la semivarianza es una medida de riesgo más plausible que la varianza, debido a que solo tiene en cuenta las desviaciones adversas (Markowitz, 1991). Matemáticamente la semivarianza es el valor esperado de las desviaciones negativas de los posibles resultados del rendimiento esperado al cuadrado. El riesgo de la cartera medido a través de la semivarianza se define como (Gupta et al., 2014):
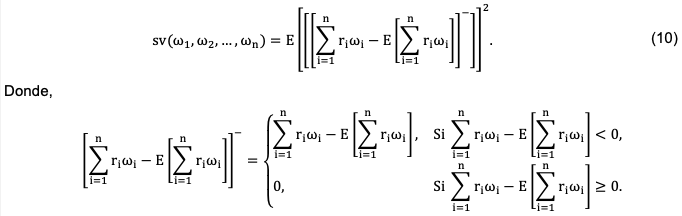
Obsérvese que al utilizar el modelo de media semivarianza no es necesario calcular la matriz de varianza-covarianza, pero la función de distribución conjunta de los activos es necesaria. Así mismo, es importante resaltar que esta medida de riesgo trata de minimizar la dispersión del rendimiento de la cartera con respecto al rendimiento esperado, pero solo cuando la primera es inferior a la última (Gupta et al., 2014). Cabe agregar que si la distribución de los rendimientos de los activos es simétrica o tiene el mismo grado de simetría, la semivarianza y la varianza producen el mismo conjunto de carteras eficientes (Markowitz, Todd, Xu, y Yamane, 1993).
La semidesviación absoluta fue propuesta por Speranza (1993) como una medida alternativa para cuantificar el riesgo. Esta autora comprobó que al tomar la función de riesgo como una combinación lineal de las semidesviaciones medias absolutas (i.e. las desviaciones medias por debajo y por encima del retorno de la cartera), se puede obtener un modelo equivalente al modelo de desviación media absoluta (Konno y Yamazaki, 1991), sí la suma de los coeficientes de la combinación lineal es positiva. En efecto, este modelo es equivalente al modelo de media varianza (Markowitz, 1952), sí los rendimientos de los activos se distribuyen normalmente. La semidesviación absoluta del rendimiento de la cartera por debajo del rendimiento esperado en el período pasado t (t = 1, 2,. . . , T), puede expresarse como (Gupta et al., 2014):
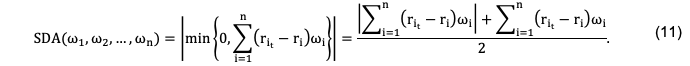
Por lo tanto, la semidesviación absoluta esperada del rendimiento de la cartera por debajo del rendimiento esperado viene dada por (Gupta et al., 2014):

El momento parcial más bajo (Lower Partial Moment)fue introducido por Bawa (1975, 1976) y Fishburn (1977), y además desarrollado y analizado por Bawa y Lindenberg (1977), Harlow y Rao (1989) y Grootveld y Hallerbach (1999). Esta media de riesgo downside provee una generalización natural de la semivarianza descrita previamente y propone medir lo que se conoce como momento parcial más bajo (Lower Partial Moment), ya que solo la parte a la izquierda de un valor objetivo de la distribución de una variable es utilizada para su cálculo. En otras palabras, consiste en ajustar la función de distribución por debajo de un umbral u objetivo determinado (Manzana, 2009). El momento parcial más bajo viene dado por (Fabozzi et al., 2010):
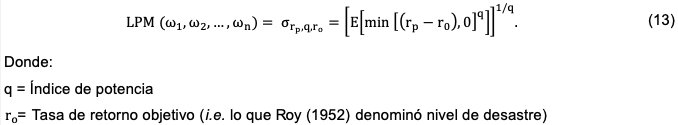
Nótese que al establecer q = 2 y igual al rendimiento esperado se obtiene la semivarianza. Además, Fishburn comprobó que q = 1 representa un inversor de riesgo neutro, mientras que 0 < q ≤ 1, y, q > 1 corresponden a un inversor amante del riesgo (risk-seeking) y a un inversor adverso al riesgo (risk-averse), respectivamente (Fabozzi et al., 2006).
El Valor en Riesgo (VaR) fue desarrollado por primera vez por J.P. Morgan a principios de la década de 1990 y puesto a disposición a través del software Risk-Metrics™ en octubre de 1994 (J.P.Morgan,1996). El VaR se centra en determinar la máxima perdida esperada asociada al riesgo de mercado que puede sufrir una cartera, en un horizonte temporal determinado, bajo unas circunstancias normales de los mercados y para un nivel de confianza dado (Gordon, 2009; Moscoso, 2014). Desde el punto de vista matemático, el nivel de confianza de una cartera en cierto horizonte de tiempo t es el retorno de la cartera tales que la fracción de los retornos será mejor que el en el horizonte de tiempo. Más formalmente, el nivel de confianza de una cartera se define como el (1-)-percentil de la distribución de los retorno de la cartera (Chapados, 2011):
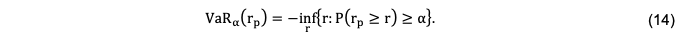
Donde:
P = Función de probabilidad
El VaR resulta útil para los tomadores de decisiones debido a que proporciona una cifra expresada en unidades monetarias que resume la exposición de un activo financiero al riesgo de mercado, lo cual facilita su comprensión. No obstante, el uso del VaR presenta algunos problemas prácticos y computacionales los cuales fueron analizados por Gordon y Baptista (2002), Gaivoronski y Pflug (2005), y, Mittnik, Rachev y Schwartz (2002). En efecto, el VaR tiene varias propiedades que no son deseables en una medida de riesgo:
i) El VaR no posee la propiedad de subaditividad, por lo que la cuantía del VaR de una cartera formada por dos subcarteras puede ser mayor que la suma de los riesgos individuales de ambas. La propiedad de subaditividad es la descripción matemática del efecto de la diversificación y por lo tanto no es razonable pensar que una cartera más diversificada tendría un mayor riesgo (Fabozzi et al., 2007; Scutellà y Recchia, 2013).
ii) Cuando el VaR se calcula a partir de la generación o simulación de escenarios, resulta ser una función no lisa y no convexa de las carteras. En consecuencia, la función VaR tiene múltiples puntos estacionarios, haciendo que resulte más difícil encontrar el valor óptimo en el proceso de optimización de la cartera (Fabozzi et al., 2010);
iii) El VaR le da poca importancia a las pérdidas más extremas o extraordinarias, debido a que no refleja adecuadamente la asimetría y la curtosis de la distribución (Moscoso, 2014).
iv) El supuesto de normalidad sobrestima el VaR para valores percentiles muy altos, mientras que subestima los valores de percentiles bajos los cuales corresponden a los eventos extremos o extraordinarios (Moscoso, 2014).
Las deficiencias en el VaR conducen a Artzner et al. (1999) a derivar cuatro propiedades deseables que debería cumplir una medida de riesgo para ser denominada “coherente”. En la misma línea, Rockafellar y Uryasev (2000, 2002) proponen el Valor en Riesgo Condicional (CVaR) como una medida “coherente” que describe el tamaño promedio que puede tener las pérdidas que están por encima del nivel de VaR estimado, de modo que provee información adicional sobre la cola de la distribución de pérdidas y ganancias de una cartera (Moscoso, 2014). Desde el punto de vista matemático, la expresión del CVaR se define como (Chapados, 2011):

Figura 3
CVaR y VaR para una Distribución t de Student

Fuente: Chapados (2011)
Una de las ventajas del CVaR se fundamenta en que analiza los rendimientos inferiores al VaR, cuantificando la pérdida esperada en ese escenario. A modo de ejemplo, dos carteras pueden tener igual VaR y aparentar poseer el mismo nivel de riesgo, no obstante, al analizar el CVaR se podrá determinar que la cartera de mayor riesgo será la que cuente con el mayor CVaR. Como se observa, el análisis de esta situación se escapa al análisis del VaR, por lo que se prefiere en algunas ocasiones trabajar con el CVaR. Como se aprecia, el VaR nunca será mayor que el CVaR, por ello, las carteras con bajo CVaR tendrán un VaR aún menor. Otra de las ventajas del CVaR en su utilidad especialmente cuando la distribución de los retornos de los activos no es continua y lejos de la hipótesis de normalidad (Moscoso, 2014). Las propiedades del CVaR son analizadas en detalle por Acerbi y Tasche (2002), Gordon (2009), y, Rockafellar y Uryasev (2002). La ubicación del VaR en una distribución hipotética del retorno de un activo y su relación con el CVaR se presentan en la figura 3.
En la optimización de carteras el riesgo de mercado, esto es, el riesgo de la variación de los activos financieros que conforman una cartera dada, se puede medir utilizando medidas de riesgo de dispersión. Los enfoques comunes que utilizan este tipo de medidas de riesgo son el modelo seminal de media varianza y el modelo de desviación media absoluta.
El modelo de media varianza fue publicado hace 67 años, y es poco probable que su popularidad e impacto tanto en el entorno académico e investigador como en la industria financiera desaparezcan en el futuro. La hipótesis básica de este modelo es que las preferencias de un inversor se pueden representar por la función cuadrática (i.e. función de utilidad) del rendimiento esperado y la varianza de la cartera. Así mismo, el principio básico subyacente de este modelo clásico es que los inversionistas actúan racionalmente y sus decisiones siempre estarán orientadas a maximizar la rentabilidad esperada para un determinado nivel de riesgo o minimizar el riesgo soportado para un determinado nivel de rentabilidad esperada.
Con el modelo de media varianza Markowitz introdujo por primera vez el concepto de diversificación a través de la noción estadística de la covarianza entre los activos individuales, y la desviación estándar global de la cartera. Antes de la publicación de esta teoría, la literatura financiera había tratado la interacción entre el retorno y el riesgo de una manera ad hoc.
El modelo de desviación media absoluta es equivalente al modelo de media varianza si los rendimientos siguen una distribución normal multivariante. No obstante, cuando los rendimientos de los activos de una cartera son típicamente asimétricos, la varianza y la desviación absoluta no son apropiadas para medir el riesgo de la cartera debido a que este tipo de medidas de riesgo no hace distinción entre ganancias y pérdidas respecto del valor esperado del rendimiento. Con el propósito de resolver este conflicto, en los últimos años se han propuesto diversas medidas de riesgo denominadas downside, es decir, que solo consideran como arriesgado los resultados por debajo de cierto nivel de referencia. Las medidas de riesgo downside más comunes son: safety-risk , semivarianza, semidesviación absoluta, lower partial moment, VaR y CVaR.
El modelo de media semivarianza y el modelo de media varianza producen el mismo conjunto de carteras eficientes si la distribución de los rendimientos de los activos es simétrica o tienen el mismo grado de simetría. Así mismo, el modelo de semidesviación media absoluta es equivalente al modelo de media varianza si los rendimientos de los activos se distribuyen normalmente.
El planteamiento del enfoque de media varianza y safety-risk es dual. Markowitz concede más importancia al riesgo como factor determinante de las preferencias del inversor a la hora de formar la cartera, mientras que Roy se inclina por la determinación de una rentabilidad mínima. Así mismo, quedo patente que desde el punto de vista matemático ambos modelos se reducen a lo mismo, salvo algunas excepciones presentadas en el capítulo.
La medida de riesgo lower partial moment es una generalización natural de la semivarianza. Por otra parte, respecto a la medida del riesgo del VaR, se puede concluir que es una medida útil para medir la exposición de un activo financiero al riesgo de mercado. No obstante, el uso del VaR presenta algunos problemas prácticos y computacionales. En este propósito, la media de riesgo del CVaR se propuso para corregir las deficiencias presentadas con el VaR.
Acerbi, C., & Tasche, D. (2002). On the coherence of expected shortfall. Journal of Banking & Finance, 26(7), 1487–1503. https://doi.org/10.1016/S0378-4266(02)00283-2
Arribas, I., García, F., Guijarro, F., Olive, J., & Tamošiūnienė, R. (2016). Mass appraisal of residential real estate using multilevel modelling. International Journal of Strategic Property Management, 20(1), 77–87. https://doi.org/10.3846/1648715X.2015.1134702
Artzner, P., Delbaen, F., Eber, J. M., & Heath, D. (1999). Coherent Measures of Risk. Mathematical Finance, 9(3), 203–228. https://doi.org/10.1111/1467-9965.00068
Azmi, R. (2013). Investment Portfolio Selection Using Goal Programming: An Approach to Making Investment Decisions. Newcastle: Cambridge Scholars Publishing.
Ballestero, E., Pérez-Gladish, B., & Garcia-Bernabeu, A. (2015). The Ethical Financial Question and the MCDM Framework. In E. Ballestero, B. Pérez-Gladish, & A. Garcia-Bernabeu (Eds.), Socially Responsible Investment. International Series in Operations Research & Management Science (Vol. 219, pp. 3–22). Springer, Cham. https://doi.org/10.1007/978-3-319-11836-9_1
Bawa, V. S. (1975). Optimal rules for ordering uncertain prospects. Journal of Financial Economics, 2(1), 95–121. https://doi.org/10.1016/0304-405X(75)90025-2
Bawa, V. S. (1976). Admissible Portfolio for All Individuals. The Journal of Finance, 31(4), 1169–1183. https://doi.org/10.1111/j.1540-6261.1976.tb01967.x
Bawa, V. S., & Lindenberg, E. B. (1977). Capital market equilibrium in a mean-lower partial moment framework. Journal of Financial Economics, 5(2), 189–200. https://doi.org/10.1016/0304-405X(77)90017-4
Bermúdez, J. D., & Vercher, E. (2012). Selección de carteras mediante un algoritmo evolutivo con múltiples objetivos. In VIII Congreso Español sobre Metaheurística, Algoritmos Evolutivos y Bioinspirados (MAEB 2012) (pp. 383–389). Albacete (España).
Boza Valle, J. A., Manjarrez Fuentes, N. N., & Vega De La Cruz, L. O. (2018). Evaluación multicriterio del control interno en una entidad hotelera. Espacios, 39(48).
Chapados, N. (2011). Portfolio choice problems: an introductory survey of single and multiperiod models. Springer.
Chen, J. M. (2016). Postmodern Portfolio Theory. New York: Palgrave Macmillan US. https://doi.org/10.1057/978-1-137-54464-3
Dassan, E. F., Santos, D., Da Silva, A. M., Kawamoto, L. T., & Rodrigues, E. F. (2016). Otimização Multiobjetivo em uma Linha de Produção de Placas Eletrônicas de uma Pequena Empresa. Espacios, 37(26).
Dowd, K. (2002). Measuring market risk. John Wiley & Sons.
Fabozzi, F. J., Focardi, S. M., & Kolm, P. N. (2006). Financial modeling of the equity market: from CAPM to cointegration. Wiley.
Fabozzi, F. J., Focardi, S. M., & Kolm, P. N. (2010). Quantitative equity investing: techniques and strategies. John Wiley.
Fabozzi, F. J., Kolm, P. N., Pachamanova, D. A., & Focardi, S. M. (2007). Robust portfolio optimization and management. John Wiley.
Fishburn, P. C. (1977). Mean-Risk Analysis with Risk Associated with Below-Target Returns. The American Economic Review, 67(2), 116–126. https://doi.org/10.2307/1807225
Gaivoronski, A. A., & Pflug, G. C. (2005). Value-at-risk in Portfolio Optimization: Properties and Computational Approach. Journal of Risk, 7(2), 1–31.
García, F., González-Bueno, J., Oliver, J., & Tamošiūnienė, R. (2019). A credibilistic mean-semivariance-PER portfolio selection model for Latin America. Journal of Business Economics and Management, 20(2), 225–243. https://doi.org/10.3846/jbem.2019.8317
García, F., Guijarro, F., & Moya, I. (2013). A multiobjective model for passive portfolio management: an application on the S&P100 index. Journal of Business Economics and Management, 14(4), 758–775. https://doi.org/10.3846/16111699.2012.668859
García, F., Guijarro, F., Oliver, J., & Tamošiūnienė, R. (2018). Hybrid fuzzy neural network to predict price direction in the german DAX-30 index. Technological and Economic Development of Economy, 24(6), 2161–2178. https://doi.org/10.3846/tede.2018.6394
García, J., Sánchez, M. Á., & Trinidad, J. E. (1998). El principio primero la seguridad de Roy y su derivación hasta el modelo de Markowitz. Cuadernos Aragoneses de Economía, ISSN 0211-0865, Vol. 8, No 2, 1998, Págs. 423-429, 8(2), 423–429.
Gitman, L. J., & Joehnk, M. D. (2009). Fundamentos de inversiones (10th ed.). Mexico: Pearson Educacion, Inc.
Gordon, A. (2009). From Markowitz to modern risk management. The European Journal of Finance, 15(5–6), 451–461. https://doi.org/10.1080/13518470902853566
Gordon, A., & Baptista, A. (2002). Economic implications of using a mean-VaR model for portfolio selection: A comparison with mean-variance analysis. Journal of Economic Dynamics and Control, 26(7–8), 1159–1193. https://doi.org/10.1016/S0165-1889(01)00041-0
Grootveld, H., & Hallerbach, W. (1999). Variance vs downside risk: Is there really that much difference? European Journal of Operational Research, 114(2), 304–319. https://doi.org/10.1016/S0377-2217(98)00258-6
Gupta, P., Mehlawat, M. K., Inuiguchi, M., & Chandra, S. (2014). Portfolio Optimization: An Overview. In Fuzzy Portfolio Optimization. Studies in Fuzziness and Soft Computing (Vol 316, pp. 1–31). Springer-Verlag Berlin Heidelberg. https://doi.org/10.1007/978-3-642-54652-5_1
Harlow, W. V., & Rao, R. K. S. (1989). Asset Pricing in a Generalized Mean-Lower Partial Moment Framework: Theory and Evidence. The Journal of Financial and Quantitative Analysis, 24(3), 285–311. https://doi.org/10.2307/2330813
J.P.Morgan. (1996). Riskmetrics technical document (4th ed.). New York: Morgan Guaranty Trust Company of New York.
Kolm, P. N., Tütüncü, R., & Fabozzi, F. J. (2014). 60 Years of portfolio optimization: Practical challenges and current trends. European Journal of Operational Research, 234(2), 356–371. https://doi.org/10.1016/j.ejor.2013.10.060
Konno, H. (1988). Portfolio optimization using L1 risk measure (IHSS Repor). Institute of Human and Social Sciences, Tokyo Institute of Technology.
Konno, H. (1990). Piecewise linear risk functions and portfolio optimization. Journal of the Operations Research Society of Japan, 33(2), 139–156. https://doi.org/10.15807/jorsj.33.139
Konno, H., & Yamazaki, H. (1991). Mean-Absolute Deviation Portfolio Optimization Model and Its Applications to Tokyo Stock Market. Management Science, 37(5), 519–531. https://doi.org/10.1287/mnsc.37.5.519
Manzana, V. A. (2009). Teorías sobre coberturas con contratos de futuro. Cuadernos de Economía, 28(50), 157–190.
Markowitz, H. (1952). Portfolio Selection. The Journal of Finance, 7(1), 77–91. https://doi.org/10.1111/j.1540-6261.1952.tb01525.x
Markowitz, H. (1959). Portfolio selection: efficient diversification of investments. New York: Jhon Wiley & Sons, Inc.
Markowitz, H. (1991). Foundations of Portfolio Theory. The Journal of Finance, 46(2), 469–477. https://doi.org/10.1111/j.1540-6261.1991.tb02669.x
Markowitz, H., Todd, P., Xu, G., & Yamane, Y. (1993). Computation of mean-semivariance efficient sets by the Critical Line Algorithm. Annals of Operations Research, 45(1), 307–317. https://doi.org/10.1007/BF02282055
Masood, O., Tvaronavičienė, M., & Javaria, K. (2019). Impact of oil prices on stock return: evidence from G7 countries. Entrepreneurship and Sustainability Issues, 1(2), 129–137. https://doi.org/10.9770/ird.2019.1.2(4)
McNeil, A. J., Frey, R., & Embrechts, P. (2005). Quantitative risk management: concepts, techniques and tools. Princeton University Press.
Metaxiotis, K., & Liagkouras, K. (2012). Multiobjective Evolutionary Algorithms for Portfolio Management: A comprehensive literature review. Expert Systems with Applications, 39(14), 11685–11698. https://doi.org/10.1016/j.eswa.2012.04.053
Mittnik, S., Rachev, S., & Schwartz, E. (2002). Value-at-risk and asset allocation with stable return distributions. AStA Advances in Statistical Analysis, 86(1), 53–68.
Montoya, A. L., Rave, A. S., & Castaño, B. J. (2006). Metodologías para la medición del riesgo financiero en inversiones. Scientia Et Technica, XII(32), 275–278.
Moscoso, J. A. (2014). Distribuciones de probabilidad alternativas para la gestión de riesgo en mercados financieros (Ph.D. dissertation). Universitat de Valencia.
Nanpeng Yu, Somani, A., & Tesfatsion, L. (2010). Financial risk management in restructured wholesale power markets: Concepts and tools. In IEEE PES General Meeting (pp. 1–8). Providence, RI, USA: IEEE. https://doi.org/10.1109/PES.2010.5589886
Ortobelli, S., Rachev, S. T., Stoyanov, S., Fabozzi, F. J., & Biglova, A. (2005). The proper use of risk measures in portfolio theory. International Journal of Theoretical and Applied Finance, 08(08), 1107–1133. https://doi.org/10.1142/S0219024905003402
Ponsich, A., Jaimes, A., & Coello, C. A. (2013). A Survey on Multiobjective Evolutionary Algorithms for the Solution of the Portfolio Optimization Problem and Other Finance and Economics Applications. IEEE Transactions on Evolutionary Computation, 17(3), 321–344. https://doi.org/10.1109/TEVC.2012.2196800
Rockafellar, R. T., & Uryasev, S. (2000). Optimization of conditional value-at-risk. Journal of Risk, 2(3), 21–41.
Rockafellar, R. T., & Uryasev, S. (2002). Conditional value-at-risk for general loss distributions. Journal of Banking & Finance, 26(7), 1443–1471. https://doi.org/10.1016/S0378-4266(02)00271-6
Rom, B. M., & Ferguson, K. W. (1994). Post-Modern Portfolio Theory Comes of Age. The Journal of Investing, 3(3), 11–17. https://doi.org/10.3905/joi.3.3.11
Roy, A. D. (1952). Safety First and the Holding of Assets. Econometrica, 20(3), 431–449. https://doi.org/10.2307/1907413
Scutellà, M. G., & Recchia, R. (2013). Robust portfolio asset allocation and risk measures. Annals of Operations Research, 204(1), 145–169. https://doi.org/10.1007/s10479-012-1266-3
Sharpe, W. F. (1963). A Simplified Model for Portfolio Analysis. Management Science, 9(2), 277–293. https://doi.org/10.2307/2627407
Sharpe, W. F. (1966). Mutual Fund Performance. The Journal of Business, 39(1), 119–138. https://doi.org/10.2307/2351741
Shefrin, H., & Statman, M. (2000). Behavioral Portfolio Theory. Journal of Financial and Quantitative Analysis, 35(02), 127–151.
Simaan, Y. (1997). Estimation Risk in Portfolio Selection: The Mean Variance Model versus the Mean Absolute Deviation Model. Management Science, 43(10), 1437–1446. https://doi.org/10.2307/2634417
Speranza, M. (1993). Linear programming models for portfolio optimization. Finance, 14, 107–123.
Unger, A., & Poddig, T. (2014). The use of risk budgets in portfolio optimization. Friedrichsdorf: Springer Gabl.
Useche-Arévalo, A. J. (2015). Construcción de portafolios de inversión desde las finanzas del comportamiento: una revisión crítica. Cuadernos de Administración, 28(51), 11–43. https://doi.org/10.11144/Javeriana.cao28-51.cpif
Vercher, E. (2015). Soft Computing approaches to portfolio selection. Boletin de Estadística e Investigación Operativa, 31(1), 23–46.
Vercher, E., & Bermúdez, J. D. (2012). Fuzzy Portfolio Selection Models: A Numerical Study. In M. Doumpos, C. Zopounidis, & P. M. Pardalos (Eds.), Springer Optimization and Its Applications (Volumen 70, pp. 253–280). Springer, Boston, MA. https://doi.org/10.1007/978-1-4614-3773-4_10
Vercher, E., & Bermúdez, J. D. (2015). Portfolio optimization using a credibility mean-absolute semi-deviation model. Expert Systems with Applications, 42(20), 7121–7131. https://doi.org/10.1016/j.eswa.2015.05.020
Xidonas, P., Doukas, H., Mavrotas, G., & Pechak, O. (2016). Environmental corporate responsibility for investments evaluation: an alternative multi-objective programming model. Annals of Operations Research, 247(2), 395–413. https://doi.org/10.1007/s10479-015-1820-x
1. Department of Economics and Social Sciences, Universitat Politècnica de València, Valencia, 46022, Spain, fergarga@esp.upv.es
2. Faculty of Business Administration, Universidad Pontificia Bolivariana, Bucaramanga, 681017, Colombia, jairoa.gonzalez@upb.edu.co
3. Department of Economics and Social Sciences, Universitat Politècnica de València, Valencia, 46022, Spain, jaolmun@ade.upv.es
4. Faculty of Business Administration, Universidad Pontificia Bolivariana, Bucaramanga, 681017, Colombia, gladys.rueda@upb.edu.co