

Vol. 40 (Issue 38) Year 2019. Page 17
JARAMILLO-VALBUENA, Sonia 1; AUGUSTO-CARDONA, Sergio 2 y ALDANA, Jorge Alejandro 3
Received: 24/12/2018 • Approved: 25/10/2019 • Published 04/11/2019
ABSTRACT: Many internet-based applications generate data streams, among others, the financial markets, computer network, phone conversations, biological and medical applications. Streaming data presents challenges in different level that cannot be handled by traditional database management systems. Reliability, scalability, durability, lack of structure, response time are some of them. Motivated by the industry’s need to obtain useful knowledge from data streams on the fly, several clustering methods have been proposed. In particular, in this paper, we compare experimentally 5 state of the art stream clustering algorithms: StreamKM++, CluStream, DenStream, ClusTree and ClusCTA-MEWMA. We assess their robustness in the presence of noisy data. We conduct experiments based on synthetic datasets. The results show that ClusCTA-EWMA has better performance than the other algorithms in datasets with noise. |
RESUMEN: Muchas aplicaciones basadas en Internet generan streams de datos. Algunas de ellas son los mercados financieros, redes informáticas, conversaciones telefónicas, aplicaciones biológicas y médicas. El procesamiento de streams de datos representa grandes desafíos a nivel de fiabilidad, escalabilidad, durabilidad, falta de estructura, memoria y tiempo de respuesta, que no pueden ser resueltos mediante los sistemas de gestión de bases de datos tradicionales. La necesidad de obtener conocimiento útil a partir de streams de datos ha llevado a la construcción de diferentes métodos de clustering. En particular, en este documento, se comparan experimentalmente 5 algoritmos de clustering sobre streams de datos: StreamKM ++, CluStream, DenStream, ClusTree y ClusCTA-MEWMA. Se evalúa su robustez ante la presencia de ruido. Los experimentos realizados se efectúan sobre datasets sintéticos. Los resultados muestran que ClusCTA-EWMA tiene mejor rendimiento que los otros 4 algoritmos en datasets con ruido. |
Clustering algorithms are the most traditional unsupervised machine learning technique. Clustering is the process of partitioning a set of objects in subgroups (called clusters), such that objects in the same cluster are similar and objects belonging to other clusters are dissimilar (Ackermann, et al., 2012). In general, the data stream clustering takes place in two stages: online and offline. The online phase summarizes the data, and the offline creates the final clusters (Ghesmoune; Lebbah; Azzag, 2016). Data stream clustering has important applications in areas such as opinion mining, sentiment analysis, city-planning, intrusion detection, libraries, stock market analysis, earthquake studies and biomedical Text Mining (Jaramillo; Londoño; Cardona, 2108).
Data stream clustering algorithms can be broadly classified into three different categories: stream partitioning methods, density-based stream clustering methods and hierarchical stream clustering methods. The first class of algorithms, organizes the instances into clusters, which are formed using a distance function. The obtained clusters have a spherical shape (Ghesmoune; Lebbah; Azzag, 2016). Density-based stream clustering methods associate clusters to high density hyper-volumes in the feature space. Samples in low density areas are considered noise. These methods find clusters of arbitrary shapes. The main challenge of this kind of algorithms is the process of density estimation, which may be computationally expensive (Aggarwal C. , 2013). The last category represents data clusters as a binary decision-tree (or a dendrogram), which summarizes the classes and allows an easy visualization of the classifier. Once the tree is constructed, it is possible to adjust the number of clusters by splitting the dendrogram at different levels without re-executing the algorithm for the same dataset (Ghesmoune; Lebbah; Azzag, 2016).
In this paper, we compare experimentally 5 data stream clustering algorithms: StreamKM++, CluStream, DenStream, ClusTree and ClusCTA-MEWMA. The quality metric that we use is the Silhouette coefficient. For the evaluation we use datasets with different noise levels: 0%, 5%, 10%, 15%, and 20%.
The paper is organized as follows. Section 2 presents preliminaries on data stream clustering. Section 3 describes the model evaluation. The last section provides a summary of the findings in this work.
Several approaches have been proposed to data stream clustering. In this section we describe 5 known algorithms in the literature: StreamKM++, CluStream, DenStream, ClusTree and ClusCTA-MEWMA.
StreamKM++ (Ackermann M. R., et al., 2012) is a partitioning-based clustering algorithm, that works in a top-down mode. StreamKM++ uses a new data structure known as Coreset Tree to represent a coreset. A coreset is a subset of input examples, that approximates the original input instance set, such that we can get a good estimate of the solution by resolving the optimization problem on the coreset. The coreset tree is a binary data structure that performs a hierarchical divisive clustering for the set. The clustering process starts with a single cluster, which contains the complete set of examples P. Each successive iteration divides the most heterogeneous clusters into two subclusters, with the constraint that the instances in one subcluster are far from instances in the other subcluster. The process is iterated until the number of clusters corresponds to k clusters. The coreset tree fulfills 2 properties: 1) Each coreset tree node is linked with a cluster in the divisive hierarchical clustering process. 2) The coreset tree root is associated with the lone cluster. StreamKM++ is unable to detect arbitrary shapes (Jaramillo; Londoño; Cardona, 2108). StreamKM++ do not differentiate the occurrence of outliers or noise in the data stream.
CluStream is partitioning-based clustering method that uses the concepts of the concepts of microclustering and pyramidal time frame (Aggarwal, Han, Wang, & Yu, 2003). The microclusters let to compress, preserve the data temporal locality, summarize and analyze the data evolution. The pyramidal time frame technique stores data snapshots at differing time horizons. CluStream works in two phases: onlineand offline. In the first phase, CluStreamplaces each arriving example in a new microcluster or in one of the existing microclusters. Later, CluStream calculates the distance of the example to the micro-cluster centroids M1 …Mq, and evaluates based on this, if the instance naturally belong to a cluster Mi. If the instance does not lie within the boundary of the nearest micro-cluster, then CluStream generates a new micro-cluster. A microcluster disappear if it reaches its expiration time or when close microclusters merge. In the last phase, CluStream gets the final clusters running k-means on the microclusters (Aggarwal, Han, Wang, & Yu, 2003) (Jaramillo; Londoño; Cardona, 2108). CluStream do not differentiate the occurrence of outliers or noise in the data stream.
DenStream (Cao, Ester, Qian, & Zhou, 2006) is a density -based clustering algorithm that use core micro-clusters and outlier micro-clusters. The core micro-cluster lets to summarize the clusters with arbitrary shape. The outlier micro-cluster lets to distinguish outliers. DenStream considers low density areas as noise. DenStream runs the DBSCAN (Ester, Kriegel, Sander, & Xu, 1996) algorithm to set up the candidate micro-cluster set. DenStream creates a new candidate micro cluster for instance p when the total weight in this neighborhood is overhead βµ, where β (0<β≤1) is a threshold parameter and µ is an integer representing the overall weight of data points in a core object. DenStream prunes low weight micro-clusters, that is, when we < βµ. Two weaknesses of this algorithm are the time-consumed by the pruning phase for deleting outlier process and no detecting concept drift (Jaramillo; Londoño; Cardona, 2108) (Amini, Wah, & Saboohi, 2014).
ClusTree is a hierarchical clustering algorithm. ClusTree inserts instances upon arrival, from the stream into a micro-cluster. To place a new instance, ClusTree run down the hierarchy to get the leaf micro-cluster more similar to the example. Each entry defines the cluster features (CF) properties of their corresponding subtree in the hierarchy. The creation and update process ClusTree process is similar to that of any multidimensional index. The ClusTree, for insertion uses Euclidean distance and for the splitting, combines the entries in two sets such the sum of the intra-group distances is minimal. ClusTree incorporates a decay factor, to weigh down the influence of older data, thus this keeps an up-to-date view of the data distribution. For this, temporal information is added to the nodes. The value λ is a decay rate which controls how much more one favors new instances compared to old samples. If λ is higher, then the faster the ClusTree forgets old data (Kranen, Assent, Baldauf, & Seidl, 2011) (Jaramillo; Londoño; Cardona, 2108).

The clustering resulting from the ClusTree is the group of cluster features kept on the leafs. To detect clusters of arbitrary shape and noise, it is possible to apply a DBSCAN or anyother density based algorithm on the CF’s (Ghesmoune; Lebbah; Azzag, 2016) (Jaramillo; Londoño; Cardona, 2108).
ClusCTA-MEWMA, described in (Jaramillo; Londoño; Cardona, 2108) (Jaramillo; Londoño; Cardona, 2018), is a new clustering technique that uses multiple sliding windows and centroid tracking for maintaining enough knowledge about centroid behavior, and multivariate EWMA to report the occurrence of concept drift. In order for ClusCTA to start the process of tracking centroids, it must have initial centroids of good quality (even if there is noise in the data stream). ClusCTA-EWMA uses MCOD (Tran, Fan, & Shahabi, 2016) (Kontaki; Gounaris; Papadopoulos; Tsichlas.; Manolopoulos, 2011), as noise filtering method. MCOD is an approach based on microclusters that uses a priority queue to store instances and Euclidean distance to report noise.
This section describes the evaluation of the different approaches to cluster from data streams, described above. StreamKM++, CluStream, DenStream, ClusTree and ClusCTA-MEWMA are implemented on top of the Massive On-line Analysis (MOA) framework ( The University of Waikato, 2015), a widely known framework for data mining evolving data streams written in Java (Jaramillo; Londoño; Cardona, 2108). The experiments focus on assessing the quality of the clustering methods.
To evaluate the performance of each algorithm we executed a set of experiments using synthetic datasets. Synthetic datasets were created with the class RandomRBFGeneratorEvents (Bifet, Holmes, Kirkby, & Pfahringer, 2010), which is part of MOA. RandomRBFGeneratorEvents is a generator based on the random Radial Basis Function that adds drift to samples in a stream. The random radial basis function (Bifet, Holmes, Pfahringer, & Gavalda, 2009) generates a fixed number of random centroids. Each centroid is defined by the initial random position, the class label, its standard deviation, and its weight. RandomRBFGeneratorEvents creates instances by doing a weighted random selection of a centroid, which determines the label. The random radial basis function gives rise to a normally distributed hyper sphere of instances enclosing each centroid. Drift is added by moving the centroids at different rates (Jaramillo; Londoño; Cardona, 2018).
We create 5 clusters, of which 2 have no movement (speedOption=0) and 3 do. During the experiment execution, a moving cluster can change its speed (speedOption may take 3 different values: 0.01/500, 0.001/500 and 0.1/500). Speed is given as distance units in the feature space every 500 samples (Jaramillo; Londoño; Cardona, 2108).
We calculated the quality of clustering and made the comparative analysis for different noise levels: 0%, 5%, 10%, 15%, and 20%, respectively. We used the Silhouette coefficient as quality metric. We got the coefficients by using Eq. (1).

a(i) is the average distance between i and all other examples within the same cluster (intra-cluster distance) and b(i) is the the smallest average distance of i to all points not contained in its own cluster (the mean nearest-cluster distance).
The quality results obtained on synthetic datasets over time, are summarized in Figures 1-5. To analyze them we consider the Silhouette coefficient as random variables that change over time. These random variables do not follow a Gaussian distribution, therefore we used the non-parametric alternative test (Mann-Whitney U Test) to compare the collections of measures. We test the hypothesis of equal medians for two independent samples. Then we register a performance index for StreamKM++, CluStream, DenStream, ClusTree and ClusCTA-MEWMA (Jaramillo, Londoño, & Cardona).
Figure 1 reports the experimental result for a dataset without noise. From the observation, we can find that StreamKM++, CluStream, DenStream, ClusTree and ClusCTA-MEWMA have similar behavior. In this case, the analysis shows that the null hypothesis is not rejected, meaning there is not a statistical significant difference between the performances of these algorithms.
Figure 1
Clustering quality of ClusCTA-MEWMA, ClusTree, StreamKM++,
DenStreamandCluStream, noise level=0% (Silhouette index)
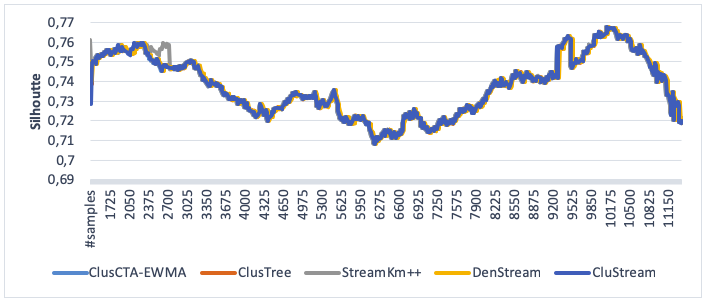
Source: Own image
From Figure 2 and Figure 3 , we observe that DenStream and ClusTree have similar behavior. In this case, the analysis shows that the null hypothesis is not rejected, meaning there is not a statistical significant difference between the performances of both algorithms (p-value = 0,9434 for alpha = 0.05).
Figure 2
Clustering quality of ClusCTA-MEWMA, ClusTree, StreamKM++
DenStreamandCluStream, noise level=5% (Silhouette index)
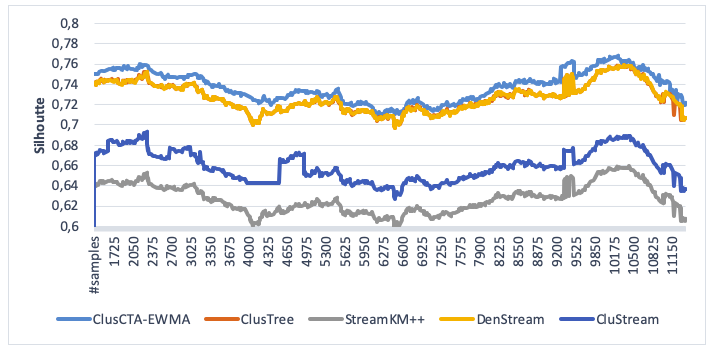
Source: Own image
-----
Figure 3
Clustering quality of ClusCTA-MEWMA, ClusTree, StreamKM++,
DenStream and CluStream, noise level=10% (Silhouette index)
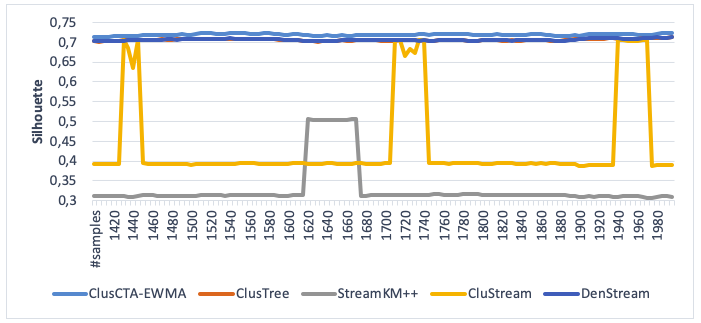
Source: Own image
-----
Figure 4
Clustering quality of ClusCTA-MEWMA, ClusTree, StreamKM++
DenStreamandCluStream, noise level=15% (Silhouette index)
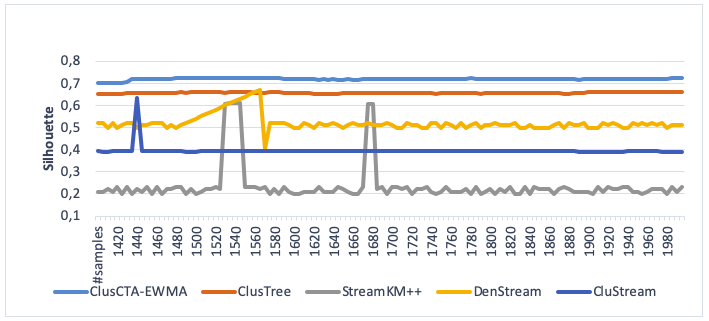
Source: Own image
-----
Figure 5
Clustering quality of ClusCTA-MEWMA, ClusTree, StreamKM++
DenStreamandCluStream, noise level=20% (Silhouette index)
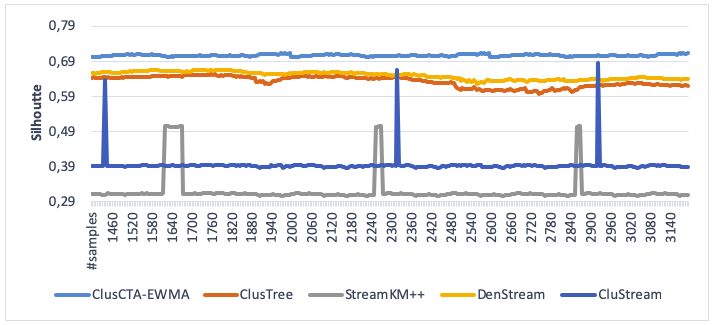
Source: Own image
From Figures 2-5, we observe that ClusCTA-EWMA outperform the other four algorithms, namely ClusTree, StreamKM++, DenStreamandCluStream, in all the test cases. The StreamKM++ algorithm shows the worst performance for all noise levels (5%, 10%, 15% and 20%).
In this paper, we compare 5 different methods to cluster data streams: StreamKM++, CluStream, DenStream, ClusTree and ClusCTA-MEWMA. We evaluate the quality of clustering produced by each of them. We use the Silhouette coefficient as quality metric. In datasets without noise, all algorithms have similar performance. With noise, ClusCTA-MEWMA shows better performance and StreamKM++ shows the worst performance for all datasets.
Each algorithm addresses the noise problem in a different way. The noise filtering process is still a challenging and interesting problem to consider for future work.
ACKERMANN, M. R., MARTENS, M., RAUPACH, C., SWIERKOT, K., LAMMERSEN, C., & SOHLER, C. (2012, may). StreamKM++: A Clustering Algorithm for Data Streams. Journal of Experimental Algorithmics JEA, 17, 1-31.
AGGARWAL, C. (2013). A survey of stream clustering algorithms. Data Clustering: Algorithms and Applications. Chapman and Hall/CRC: 2013. p. 231–58.
AGGARWAL, C., HAN, J., WANG, J., & YU, P. S. (2003). A Framework for Clustering Evolving Data Streams. Proceeding VLDB '03 Proceedings of the 29th international conference on Very large data bases, (págs. 81-92). Berlin, Germany.
AMINI, A., WAH, T. Y., & SABOOHI, H. (2014). On Density-Based Data Streams Clustering Algorithms: A Survey. Journal of Computer Science and Technology, 29(1), 116-141. Obtenido de http://dx.doi.org/10.1007/s11390-014-1416-y
BIFET, A. (2012). RandomGeneratorDrift. Recuperado el 5 de abril de 2016, de http://www.cs.waikato.ac.nz/~abifet/MOA/API/_random_r_b_f_generator_drift_8java_source.html
BIFET, A., HOLMES, G., KIRKBY, R., & PFAHRINGER, B. (2010). MOA: Massive Online Analysis. J. Mach. Learn. Res., 11, 1601-1604. Obtenido de http://dl.acm.org/citation.cfm?id=1756006.1859903
BIFET, A., HOLMES, G., PFAHRINGER, B., & GAVALDA, R. (2009). Improving Adaptive Bagging Methods for Evolving Data Streams. (págs. 23-37). Berlin, Heidelberg: Springer-Verlag. Obtenido de http://dx.doi.org/10.1007/978-3-642-05224-8_4
CAO, F., ESTER, M., QIAN, W., & ZHOU, A. (2006). Density-based clustering over an evolving data stream with noise. SIAM Conference on Data Mining, (págs. 328-339).
ESTER, M., KRIEGEL, H.-P., SANDER, J., & XU, X. (1996). A Density-based Algorithm for Discovering Clusters a Density-based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (págs. 226-231). Portland: AAAI Press. Obtenido de http://dl.acm.org/citation.cfm?id=3001460.3001507
JARAMILLO, LONDOÑO, & CARDONA. (2018). ClusCTA MEWMAChart: A clustering-based technique to detect Concept Drift in the presence of noise. Espacios, 27-41.
JARAMILLO, LONDOÑO, & CARDONA. (2108). ClusCTA: A Clustering technique based on Centroid Tracking for Data Streams. Espacios, Vol. 39(14), 25.
JARAMILLO, Sonia., LONDOÑO, Jorge M., & CARDONA, Sergio A. (2017). Performance Evaluation of Concept Drift Detection Techniques in the presence of noise. Revista Espacios, Vol.38(38).
KONTAKI, M., GOUNARIS, A., PAPADOPOULOS, A. N., TSICHLAS, K., & MANOLOPOULOS, Y. (2011). Continuous monitoring of distance-based outliers over data streams. In 2011 IEEE 27th International Conference on Data Engineering. 35-146.
KRANEN, ASSENT, BALDAUF, & SEIDL. (2011). The ClusTree Indexing Micro-clusters for Anytime Stream Mining. Journal Knowledge and Information Systems, 29(2), 249-272.
THE UNIVERSITY OF WAIKATO. (2015). MOA. Recuperado el 04 de december de 2015, de http://moa.cms.waikato.ac.nz/details/
TRAN, L., FAN, L., & SHAHABI, C. (2016). Distance based Outlier Detection in Data Streams. Proceedings of the VLDB Endowment, Vol. 9, No. 12.
1. PhD in Engineering. Computer Engineering Dept., Universidad del Quindío, UQ. Armenia, (Colombia), 57-036-7359355, sjaramillo@uniquindio.edu.co
2. PhD in Engineering. Computer Engineering Dept., Universidad del Quindío, UQ, Armenia, (Colombia), 57-036-7359355, sergio_cardona@uniquindio.edu.co
3. Master in Administration. Engineering Dept. Universidad del Quindío, UQ, Armenia, (Colombia), 57-036-7359355, jaldana@uniquindio.edu.co