ISSN 0798 1015

Vol. 40 (Number 35) Year 2019. Page 15

Application of the sequential analysis method in the justification of optimal managerial decisions in the context of uncertainty

Aplicación del método de análisis secuencial en la justificación de decisiones gerenciales óptimas en contexto de incertidumbre

KAMENETSKAYA, Natalia V. 1; MEDVEDEVA, Olga M. 2; GORBUNOV, Aleksey A 3; KHITOV, Sergey B. 4 & SMIRNOVA, Irina V. 5

Received: 08/06/2019 • Approved: 08/10/2019 • Published 14/10/2019

Contents

1. Introduction

2. Methods

3. Results

4. Discussion

5. Conclusion

Acknowledgements

Bibliographic references

1. Introduction

Development and adoption of managerial decisions by the authorities (officials, commanders (heads)) of the executive department of the Russian Federation government are aimed at developing ways of using subordinate forces and measures that are optimal in the expected conditions of the situation.

Undoubtedly, the solution formation remains a deeply creative process. However, mathematical modeling, the efficiency of which has been repeatedly confirmed in various fields of applied science over the years, helps developing possible ways of using forces and measures and choosing the optimal one, (Akbar & Beg, 2016; Fitzgibbon et al., 2014; Siddiqi et al., 2015; Giordano et al., 2013; Habib, 2016; Meerschaert, 2013; Yang, 2013; Batkovskiy et al., 2016; Gorbunov & Vasilieva, 2014; Gorbunov et al., 2017; Malygin & Schetka, 2014).

The mathematical modeling methods allow a comparative assessment of the efficiency of various planned options for action (alternatives). The remarkable property of mathematical models allows to estimate the impact of various elements of the situation on the selected efficiency indicator, taking such interconnections and interdependencies between them into account, which the human brain cannot estimate. This allows to quantitatively estimate the best options for action (the best alternatives) from among those considered by a complete enumeration of all possible options. However, this is not always feasible.

This is primarily due to the limiting factors that describe situations where decisions should be formulated and made. These factors can be divided into three main groups (Motorygin & Galishev, 2013; Malygina & Marin, 2013):

• Economic factors (money, production and human resources, time, etc.);
• Technical factors (dimensions, weight, power consumption, reliability, accuracy, etc.); and
• Social factors that account for the human ethics and morality, ensuring the safety of people, and environmental requirements.

As such, the number of compared options can be so large that the enumeration cannot be completed within the available time.

In many cases, uncertainty may arise at the time of making a decision regarding the true state of the number of elements of the situation. In this case, identifying the best course of action by simple sequential comparison of all the options will be impossible.

These circumstances necessitate the use of mathematical optimization methods for the quantitative justification of decisions. Such methods, as well as the decision-making models obtained with their help, can be divided into the following groups:

• Methods and models used in conditions of certainty (reliable knowledge of situation elements) (Balychev et al., 2018);
• Methods and decision-making models used in the context of risk. The following criteria are applied for choosing the "optimal solution" in these models: a) minimization of expected losses (Batkovskiy et al., 2017); b) maximization of the expected result expressed as cash payments; and c) maximization of the expected result as a utility value (Motorygin & Galishev, 2013); and
• Methods and models used in the context of uncertainty regarding the true state of the situation elements.

In the context of uncertainty, the operational tactical formulation of the simulation problem should contain all the information required for the mathematical formulation of the problem and the choice of the optimization method.

First of all, it is required to formulate the purpose of using forces and measures. This needs to be done to determine the performance indicator. After that, the optimization purpose and the way to implement the plan are indicated. The optimization structure may vary, depending on whether the plan can be adjusted during its implementation.

After that, it is advisable to present the following factors:

• Need to choose one of several options for action; and
• Possibility of several situation options when the task is performed by forces.

In this case:

• It is unknown in what situation the task will have to be performed at the time of making a decision; and
• Various options of actions are optimal at various options of an expected situation.

Both the number of options for action and the number of options for the situation can actually be finite (but not less than two) and infinite.

Next, the factor creating uncertainty is indicated, as a rule. For example, it may be the lack of knowledge of the true state of any elements of the situation as a result of objective causes, independent of the human will and consciousness.

Making a decision on the adoption of a new complex technical system, a sample of special technique, a new sample technique (ST) of measures when performing a task depends on the knowledge of probabilistic characteristics in some cases. They can be the probability of a failure-free equipment operation, probability of completing a task, dispersion of a normally distributed random variable, etc. At the same time, the required probability characteristic is unknown and can only be estimated through a specially arranged experiment (training, test).

It is known (Wentzel, 2009; Wentzel, 2010; Kremer, 2012) that the researcher does not receive the true values of random variables, but their statistical estimates, when processing the experimental data. The more the data are processed, the more accurate and reliable these estimates are. However, better accuracy and reliability can be associated with the influence of such limiting factors as the large waste of effort, money, and time for testing. Besides, the increase in the specimens’ testing, especially expensive and single-use, for determining suitability for use (arming), leads to the decrease in their number. Better accuracy and reliability of statistical estimates for such equipment samples is not always possible and appropriate to achieve through more tests.

In such cases, SAM developed by the Hungarian mathematician Wald (1947), is a fairly efficient mathematical method. It allows to justify the choice in conditions when it depends on the knowledge of some unknown probabilistic characteristic, where a limited number of tests can be conducted for its determination or estimation.

2. Methods

The key advantage of the SAM in comparison with the classical methods of mathematical statistics is that it requires significantly smaller number of observations, which allows to make a guaranteed scientifically grounded managerial decision, provided the above conditions and restrictions.

Unlike other statistical methods, the required number of observations is not determined in advance in the SAM, and the results of the experiment are evaluated after each test. In this case, two hypotheses are considered: about conformity ( ) and nonconformity ( ) of the process under study with the requirements (sample of a complex technical system, ST of forces, achieved level of training, etc.). These requirements are set by some probabilistic characteristic.

One of three solutions is recommended after each test:

• Accept an ST as complying with the requirements (implementation of hypothesis ).
• Reject an ST (implementation of hypothesis ).
• Conduct another test, because the obtained information is insufficient for accepting or rejecting hypothesis or .

If the first or the second decision is made, the experiment ends; if the third decision is made, then it continues. Therefore, the number of tests is a random variable.

The sequential analysis does not allow to completely remove the uncertainty regarding the true value of the required probability characteristic. In this regard, it can be recommended to accept an unsuitable sample of equipment or reject the best ST when performing the task, according to test data. The fewer are the observations, the greater is the possibility of such errors.

To determine the SAM scope, the specific features are required that distinguish it from the already known features. These features can be identified if the essence of the method is known. The following reasoning can be provided to clarify it.

The requirements for the technique sample or any process on reliability, probability of completing the task, dispersion, etc. should be determined prior to the experiment.

Let us review the possibility of mathematical modeling for making scientifically based decisions on the adoption of a new ST of actions based on checking its compliance with the performance requirements (Kamenetskaya et al., 2017a).

3. Results

3.1. Justification of a managerial decision on the efficiency of the new sample technique for fire fighting and rescue efforts

One of the key areas contributing to the solution of the EMERCOM FERU tasks is the development of new sample techniques (STs) for conducting operational actions on fires and in the aftermath of emergency situations (ES).

Undoubtedly, the adoption of new STs of action by FERU should be preceded by a series of experiments (training) proving their higher efficiency (according to specified criteria) compared to the existing ones.

However, the limiting factors that have significant impact on the possibility of experiments related to the use of such methods of FERU actions in various dangerous situations include significant waste of effort, time, and money. In addition, the experiment is impossible in cases where it is associated with a threat to the life or health of people.

Problem setting. Based on the analysis of the FERU operational activities, a new ST has been developed to fight fires and conduct rescue efforts (eliminating emergency consequences).

The requirements are determined that a new ST must meet (Rodionov, 2003). For example, the probability of fighting a fire in a standard time is specified or the mathematical expectation of the maximum prevented material damage caused by an emergency (fire), which must be not less than a specified value. To estimate the efficiency of a new ST, it should be tested in training (tests). The expediency of adopting a new ST should be determined on the basis of a limited number of such trainings with the SAM use.

The probability that fire will be extinguished in time not exceeding the given is taken as a probability characteristic and performance criterion:

Figure 1
Zones of values of the possible
threshold probability p'

Figure 2
Zones of values of ratio µ when checking a new ST

3.2. Practical implementation of the SAM when testing the new ST. Graphic interpretation of the method

Figure 3
Chart of the sequential
analysis of the new ST

3.3. Tabular interpretation of the method

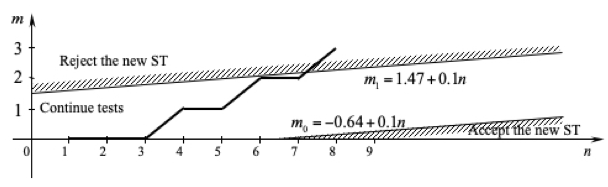
Table 1
Data of possible test option

As a result of a sequential analysis after the eighth check, a decision was made that the new ST of the actions of the FERU did not meet the requirements for the fire fighting efficiency criterion; therefore, more efficient ST should be considered.

3.4. Operational characteristics of the SAM criterion

An important characteristic of the described process is the probability that it will end with the adoption of one of two hypotheses, i.e., with the conclusion that the ST should be considered efficient and recommended for use, for example.

This probability is called the power function of a test in the literature devoted to the SAM (Wald, 1947).

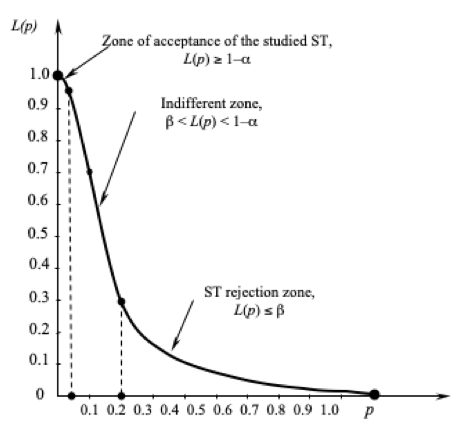
Figure 4
A chart of the operational characteristics of the criterion
in the sequential analysis of the feasibility of the new ST

4. Discussion

The application of SAM in an applied task to develop an optimal managerial decision in the context of uncertainty has been demonstrated in the article, which is devoted to making a conclusion about the efficiency of new ST for fighting fires and rescue efforts.

The considered example of the practical application of the SAM illustrates the solution of this problem with the following results:

 – Eight trainings were required with the use of the new ST of FERU actions to make a conclusion that this technique did not meet the requirements set by the criterion of efficiency in fighting fires, and more efficient ST should be considered;

 – At selected values of α and β, the power of the criterion, determined by its power function, is quite high (Figure 4), and the approximate value of the average expected number of tests is 10.

The advantage of the SAM over the classical methods of mathematical statistics is shown in the particular example, which consists in the fact that this method allows to make a guaranteed scientifically-based managerial decision with a small number of tests in the context of uncertainty.

The formulas on which the SAM is based are substantiated. The possibilities of its practical implementation in two forms – graphical and tabular – are reviewed.

The SAM can be applied to solve a wide range of planning and management tasks in various areas:

 – To develop optimal managerial decisions in the operational activities of the EMERCOM of Russia with little effort and resources;

 – To conduct a comparative assessment of the efficiency of two actions or processes (Kamenetskaya et al., 2017b);

 – To check the batch of products for compliance with specifications;

 – To develop recommendations for the acceptance of one of the competing types of equipment to be tested;

 – To develop recommendations when checking of a normally distributed random variable with unknown dispersion or with unknown expectation for compliance with the requirements;

 – To develop recommendations on the feasibility of adopting a new model of fire fighting equipment that has been modernized; and

 – To check the compliance of the range of fire fighting equipment with the specifications.

The advantages of the SAM also include the relative simplicity of its practical application: the mathematical modeling of the above tasks requires only a statement of the success or failure of a particular test performed, which corresponds to two possible values of some random variable: 0 or 1.

5. Conclusion

The advantage of the SAM over other methods lies in its ability to significantly reduce the number of experiments required to collect statistical information. As such, in particular, there is the possibility of forming a guaranteed and scientifically grounded decision on the expediency of applying new STs of FERU actions with relatively little forces and measures.

There is a wide range of technical, economic, and military planning and management tasks similar to those reviewed, for which the use of the SAM ensures relative simplicity, accessibility, fairly high accuracy and reliability of conclusions (Diner, 1969; Kamenetskaya et al., 2017a; 2017b; Volgin et al., 1981).

Acknowledgements

The authors are grateful to the Doctor of Technical Sciences, Professor V.Ya. Trofimets for his constructive comments on the essence of the problem.

6. Bibliographic references

Akbar, N.S., & Beg, O.A. (eds.). (2016). Modeling and simulation in engineering sciences. New York: iTexLi, 289 p. DOI: 10.5772/62109.

Diner, I.Y. (1969). Issledovaniye operatsiy [Operations’ research]. Leningrad: Naval Academy Publ., 605 p (in Russian).

Balychev, S.Yu., Batkovskiy, A.M., Kravchuk, P.V., Trofimets, E.N. & Trofimets, V.Ya. (2018). Situational modeling of transportation problems: applied and didactic aspects. Espacios, 39 (10), 27. Retrieved from: https://www.revistaespacios.com/a18v39n10/a18v39n10p27.pdf

Batkovskiy, A.M., Semenova, E.G., Trofimets, E.N., Trofimets, V.Ya., & Fomina, A.V. (2016). Computer Modeling of Leasing Operations. Indian Journal of Science and Technology, 9(28), 2-12. DOI: 10.17485/ijst/2016/v9i28/97661.

Batkovskiy, A.M., Semenova, E.G., Trofimets, E.N., Trofimets, V.Ya., & Fomina, A.V. (2017). Statistical simulation of the break-even point in the margin analysis of the company. Journal of Applied Economic Sciences, Romania: European Research Centre of Managerial Studies in Business Administration, Volume XII, 2(48), 558-570.

EMERCOM of Russia. (2010). Methodical recommendations on the actions of units of the federal firefighting service for extinguishing fires and conducting emergency rescue operations. Approved by the order of Emercom of Russia on 26.05.2010 No. 43-2007-18 (in Russian). Retrieved from: http://lawru.info/dok/2010/05/26/n220225.htm.

Fitzgibbon, W., Kuznetsov, Yu.A., Neittaanmäki, P., & Pironneau, O. (eds.). (2014). Modeling, simulation and optimization for science and technology. Amsterdam: Springer, 248 p. DOI: 10.1007/978-94-017-9054-3.

Giordano, F.R., Fox, W.P., & Horton, S.B. (2013). A first course in mathematical modeling. 5th ed. Boston: Cengage Learning, 704 p.

Gorbunov, A.A., & Vasilieva, A.I. (2014). The control system of civil protection. Problemy upravleniya riskami v tekhnosfere [Problems of Technosphere Risk Management], 2(30), 91-95 (in Russian).

Gorbunov, A.A., Shangin, V.N., & Ponomorchuk, A.Yu. (2017). Solution of the task of optimizing the location of the elements of the grouping of the forces for the liquidation of the consequences of emergencies of the rses. Problemy upravleniya riskami v tekhnosfere [Problems of Technosphere Risk Management], 2(42), pp. 31-36 (in Russian).

Habib, M. (ed.). (2016). Empirical modeling and its applications. New York: ExLi4EvA, 146 p. DOI: 10.5772/61406.

Kamenetskaya, N.V., Medvedeva, O.M., Khitov, S.B., & Bardulin, E.N. (2017a). Justification of effective tactical procedure choice fire fighting wrecking by means of sequential analysis method. Pozharovzryvobezopasnost [Fire and Explosion Safety], 26(5), 5–12 (in Russian). DOI: 10.18322/PVB.2017.26.05.5-12.

Kamenetskaya, N.V., Medvedeva, O.M., Khitov, S.B., & Gromov, V.N. (2017b). Comparative analysis of two tactical procedures of fire exercise and carrying out emergency rescue operations by the fire divisions of the MES of Russia. Pozharovzryvobezopasnost [Fire and Explosion Safety], 26(10), 20-26 (in Russian). DOI: 10.18322/PVB.2017.26.10.20-26.

Kremer, N.Sh. (2012). Teoriya veroyatnostey i matematicheskaya statistika [Probability theory and mathematical statistics], 3rd ed. Moscow: UNITY-DANA, 552 p.

Malygina, E.A., & Marin, M.L. (2013). The role of human factor in transport safety problem. Problemy upravleniya riskami v tekhnosfere [Problems of Technosphere Risk Management], 2(26), 19-26 (in Russian).

Malygin, I.G., & Schetka, A.V. (2014). An algorithm for optimizing information flows in automated control system forces and means of EMERCOM of Russia. Problemy upravleniya riskami v tekhnosfere [Problems of Technosphere Risk Management], 4(32), 74-78 (in Russian).

Meerschaert, M.M. (2013). Mathematical modeling, 4th ed. New York: Academic Press, 368 p.

Motorygin, Yu. D., & Galishev, M. A. (2013). Stochastic methods of decision-making for decreas probability of emergencies. Problemy upravleniya riskami v tekhnosfere [Problems of Technosphere Risk Management], 4(28), 59-64 (in Russian).

Rodionov, E. G. (2003). The duration of extinguishing fires on exits of certain categories. In: Materialy 12 nauchno-tekhnicheskoy konferentsii “Sistemy bezopanosti-2003” [Proceedings of 12 Scientific-Technical Conference “Safety Systems–2003”]. Moscow: State Fire Academy of Emercom of Russian Publ., (in Russian). Available at: http://agps-2006.narod.ru/konf/2003/sb-2003/sec-2/16.pdf.

Siddiqi, A.H., Manchanda, & P., Bhardwaj, R. (2015). Mathematical models, methods and applications. New York: Springer, 309 p. DOI: 10.1007/978-981-287-973-8.

Terebnev, V.V., & Terebnev, A.V. (2003). Upravleniye silami i sredstvami na pozhare [Managing forces and measured in a fire]. Study guide / ed. by E.A. Meshalkin. Moscow: Academy of the State Fire Service of the EMERCOM of Russia, 261 p.

Volgin, N.S., Makhrov, N.V., & Yurovskiy, V.A. (1981). Issledovaniye operatsiy [Operations’ research]. Leningrad: Naval Academy Publ., 605 p (in Russian).

Wald, A. (1947). Sequential analysis. New York: John Wiley & Sons, Inc., 221 p.

Wentzel, E.S. (2009). Issledovaniye operatsiy. Zadachi, printsipy, metodologiya [Operations’ research. Tasks, principles, methodology]. Moscow: Science, 207 p.

Wentzel, E.S. (2010). Teoriya veroyatnostey [Probability theory], 11th ed. Moscow: KnoRus, 576 p.

Yang X.-S.(ed.) (2013). Mathematical modeling with multidisciplinary applications. New York: John Wiley & Sons, 592 p. DOI: 10.1002/9781118462706.

1. Saint Petersburg University of State Fire Service of Emercom of Russia, Russian Federation. E-mail: natalia_kamenetska@mail.ru

2. Saint Petersburg University of State Fire Service of Emercom of Russia, Russian Federation

3. Saint Petersburg University of State Fire Service of Emercom of Russia, Russian Federation

4. Saint Petersburg University of State Fire Service of Emercom of Russia, Russian Federation

5. Saint Petersburg University of State Fire Service of Emercom of Russia, Russian Federation