ISSN 0798 1015

Vol. 40 (Nº 30) Año 2019. Pág. 6

Contraste de la hipótesis de mercados fractales en el mercado latinoamericano de valores

Contrast of the fractal market hypothesis in the latin american stock markets

BALLADARES, Karen A. 1; TRINIDAD-SEGOVIA, Juan E. 2 y SÁNCHEZ-GRANERO, Miguel A. 3

Recibido: 02/05/2019 • Aprobado: 02/09/2019 • Publicado 09/09/2019

Contenido

1. Introducción

2. Metodología: Exponente de Hurst

3. Resultados

4. Conclusiones

Agradecimientos

Referencias bibliográficas

1. Introducción

Tal como señalan numerosas investigaciones Barna, Stefana & Pasca (2016); Kristoufek (2012); Kristoufek & Vosvrda (2014); Kumar & Bandi (2015); Lim (2007) la Hipótesis de eficiencia de mercados (EMH), propuesta por Fama (1965) ha sido la referencia para los estudios en el ámbito de las finanzas durante las últimas cuatro o cinco décadas.  Kristoufek & Vosvrda (2014) señalaron que la EMH es la piedra angular de las finanzas modernas; así mismo, que la idea principal de EMH es que los rendimientos ajustados al riesgo no pueden predecirse sistemáticamente y que no puede haber ganancias a largo plazo por encima de las ganancias del mercado que asumen el mismo riesgo.  La definición de EMH también está estrechamente relacionada con una noción de agentes

homogéneos racionales y la distribución Gaussiana de los rendimientos.  Por otra parte, Noakes & Rajaratnam (2016) indicaron que, en un mercado eficiente de acciones, los precios reflejan toda la información disponible, y que cualquier nueva información es asimilada rápidamente por el mercado y reflejada nuevamente en sus valores.  Fue Roberts en 1967, quien menciona que existen tres formas de eficiencia de mercados de acciones: (a) la forma débil, que describe cómo los precios de las acciones reflejan toda la información histórica de los precios y los volúmenes a negociar en el mercado; (b) la forma semi-fuerte, que postula que los precios de las acciones están determinados por cualquier tipo de información pública referente a las mismas acciones; y (c) la forma fuerte, que afirma que los precios de las acciones reflejan toda la información de las dos formas anteriores de eficiencia, añadiéndose la información que es solo conocida por agentes cercanos a las compañías que emiten las acciones.  Según Fama (1970) las siguientes serían las condiciones suficientes para que un mercado sea eficiente: (a) inexistencia de costos de transacción, (b) toda la información disponible se puede obtener sin costo por todos los participantes del mercado, (c) todos los participantes están de acuerdo con las implicaciones que la información actual existente tiene sobre los precios actuales y las distribuciones de los precios futuros de cada activo.  Por consiguiente, si un mercado reúne estas condiciones, el precio de cada activo relejaría plenamente toda la información disponible. Otros autores como Lo & MacKinlay (1988) probaron la hipótesis de la caminata aleatoria mediante la comparación de estimadores de varianza en diferentes frecuencias para un período comprendido entre 1962 y 1985.  Esta línea se ha seguido en varios artículos donde los autores tratan de analizar el grado de eficiencia de los diferentes mercados desarrollados. Lima & Tabak (2005) y Fifield & Jetty (2008) utilizaron la prueba individual Lo-MacKinlay VR para estudiar la forma débil de eficiencia para los mercados de valores chinos.  La hipótesis se prueba con nuevas pruebas de coeficiente de varianza múltiple.  Metodología similar es utilizado por Sqaulli (2006) para analizar los índices sectoriales diarios del mercado financiero de Dubai (DFM) y el Mercado de Valores de Abu Dhabi (ADSM) entre 2000 y 2005. En el caso del stock africano Mlambo & Biekpe (2017) utilizaron la correlación en serie y realizaron pruebas para estudiar la eficiencia de 10 mercados de valores africanos.

Varios autores han propuesto el exponente de Hurst como una medida de la ineficiencia del mercado de valores.  Zunino, Tabak, Pérez, Garavaglia & Rosso (2007) estudiaron la eficiencia en los rendimientos y la volatilidad de los Índices del mercado latinoamericano también a través de esta metodología.  Los resultados globales sugieren que existe una mayor dependencia a largo plazo en los retornos del mercado.  Cajueiro & Tabak (2005) estudiaron la variabilidad de los exponentes de Hurst para clasificar la eficiencia para los mercados emergentes en comparación con las economías desarrolladas.  La conclusión principal es que los países asiáticos son más eficientes que los de América Latina con la excepción de México.

Kristoufek & Vosvrda (2014) construyeron un índice de eficiencia basado en el concepto de memoria a largo plazo, memoria a corto plazo y medidas de dimensión fractal.  Aplicando la metodología en un conjunto de 41 índices bursátiles en el período comprendido entre 2000 y 2011, los autores encontraron que el mercado NIKKEI es el mercado más eficiente, mientras que los menos eficientes son América Latina, Asia y Oceanía.  Más específicamente, los mercados menos eficientes fueron IBC venezolano, KLSE de Malasia, SAX de Eslovaquia, CSE de Sri Lanka e IGRA peruano.  Finalmente, Ferreira, Dionisio & Movahed (2017) analizaron la eficiencia de los mercados de valores africanos, utilizando el exponente de Hurst para evaluar la dependencia serial.  Ellos compararon los resultados obtenidos con los mercados de valores del Reino Unido, Estados Unidos y Japón.  Los resultados mostraron la existencia de la dependencia serial estadísticamente significativa.

1.1. La hipótesis del Mercado Fractal (FMH).

Peters (1994) propone el análisis del mercado fractal, que puede resumirse como el conflicto entre aleatoriedad y el determinismo.  Por un lado, según Peters, hay analistas que sienten que el mercado es perfectamente determinista; por otro lado, hay un grupo que siente que el mercado es completamente aleatorio, destaca que existe la posibilidad de que ambos grupos tengan razón de forma limitada.  Sin embargo, lo que surge de estas verdades parciales es un análisis bastante diferente, se enfoca principalmente en el análisis r/s, el cuál puede distinguir los fractales de otros tipos de estructura de mercado.  Kristoufek (2012) consideró que la piedra angular de FMH es el enfoque en la heterogeneidad de los inversores, principalmente con respecto a sus horizontes de inversión.  El mercado consiste según la FMH en un conjunto de inversores con diferentes horizontes temporales para obtener sus ganancias, puede ser minutos, horas, semanas, meses e incluso años.  Weron & Weron (2000) rechazaron el principio de homogeneidad de los inversores en los mercados de capitales y propusieron utilizar la hipótesis de mercados heterogéneos, donde diferentes participantes del mercado, analizan eventos pasados y nuevos con diferentes horizontes temporales.  En base a esta hipótesis, estos autores utilizaron el enfoque de los mercados fractales, en donde se reconoce una dependencia exponencial, no lineal, entre la información y los horizontes de inversión con el comportamiento de los inversores.  La hipótesis del mercado fractal según Kristoufek (2012) sugiere que, durante las fases estables del mercado, todo horizonte de inversión está igualmente representado para que la oferta y la demanda en el mercado se eliminen sin problemas.  Ocurriendo todo lo contrario, en períodos inestables como “crisis”. Se trata de un concepto que está estrechamente conectado a una noción de multifractalidad y dependencia a largo plazo en la serie subyacente.  El proceso Xt se considera multifractal si tiene incrementos estacionarios cuya escala sea:

Para τ > 0 y para todo q.  H(q) es llamado exponente de Hurst generalizado y su dependencia de q separa los procesos en dos categorías: monofractal (o unifractal) para constante H(q) y multifractal cuando H(q) es una función de q.  Para q = 2, se consideró la dependencia a largo plazo de los incrementos del proceso Xt.  De igual manera, se designó H = H (2).  El exponente de Hurst está conectado a la función de autocorrelación hiperbólicamente asintótica p(k), es decir p(k) αk2H−2 para k→ ∞ (Calvet y Fisher,2008).  Para H=0.5, existe un proceso aleatorio; para H>0.5, tenemos un proceso persistente; y para H<0.5, un proceso antipersistente.  Los procesos persistentes tienen una tendencia visual pero aún permanecen estacionarios, mientras que los procesos antipersistentes cambian su signo con mayor frecuencia que los procesos aleatorios.

Así mismo, Lo (2005) propone unir los conceptos de la EHM con los principios de la conducta de los inversores.  Por otro lado, Di Matteo, Aste & Dacorogna (2005) estudian empíricamente las propiedades de tipos de cambio, índices bursátiles e instrumentos de renta fija mediante el uso del exponente de Hurst generalizado.  Mostrando que los exponentes de escala están asociados con características de mercados específicos y se puede usar para diferenciar mercados en su etapa de desarrollo. Investigaciones como la de Sánchez, Trinidad y García (2008) estudiaron la presencia de procesos de memoria a largo plazo en los mercados de capitales.  En este artículo, los autores realizaron una revisión de la metodología más utilizada hasta el momento en investigaciones respecto a los procesos de memoria a largo plazo, que son el exponente de Hurst y el análisis de rango reescalado (R/S analysis).  Propusieron dos métodos, desde el punto de vista de la geometría, para calcular el exponente de Hurst, demostrando que la simple utilización de estas técnicas puede llevar a la obtención de conclusiones equivocadas, especialmente cuando se trata de series de tiempo cortas.

Zunino, Zanin & Tabak (2010) argumentaron que el entendimiento de las series de tiempo en economía, especialmente la evolución de las secuencias de precios de acciones, ha sido objeto de estudio por parte de matemáticos y físicos durante los recientes años.  Estos autores utilizaron los conceptos físicos de complejidad y entropía para evaluar el grado de orden o de desorden de los datos de en una serie de tiempo.  Básicamente, argumentaron que a medida que los datos presentaban mayor desorden, mayor era su entropía, lo que dificultaba su predicción.  Una entropía negativa permitía un mayor grado de predictibilidad de la variable.  Esta investigación se basó en los trabajos de Bentes, Menezes y Mendes (2008), quienes introdujeron el enfoque de entropía de Shannon (1948), de Rényi (1961) y de Tsallis, Anteneodo, Borland y Osorio (2003).  Onali y Goddard (2011) por otra parte, llevaron a cabo análisis fractales en mercados de acciones europeos y de Estados Unidos, encontrando evidencia de dependencia en el largo plazo en los logaritmos de los retornos de las acciones dispuestas en series de tiempo.  Estos resultados contradicen la hipótesis de eficiencia de mercados de Fama (1965).  Estos autores, señalaron que corrigiendo la dependencia a corto plazo se puede determinar la dependencia a largo plazo, sugiriendo que el mercado es eficiente, cuando en realidad no lo es.  Lo (2012) plantea la necesidad de incorporar la hipótesis de mercados adaptativos (AMH), una alternativa a la EMH que reconcilia la contradicción entre sesgos de comportamiento, enfocándose en la respuesta del comportamiento humano a las condiciones cambiantes de los mercados financieros, bajo el contexto de la agitación del mercado en el 2011 y la popularidad de la EMH en dicha década.  Contrario a la corriente de la época, el autor considera que la EMH no está equivocada; es simplemente incompleta.  Los mercados se comportan bien la mayor parte del tiempo, pero como cualquier otra invención humana, no son infalibles y pueden descomponerse de vez en cuando por razones comprensibles y predecibles.  Sánchez, Fernández & Trinidad (2012) indicaron que las investigaciones a lo largo de los últimos 50 años se podían agrupar en dos tendencias: (a) aquellos que consideraban que los precios de las acciones siguen el movimiento Browniano; y (b) aquellos que quieren demostrar que los precios siguen un movimiento Browniano fractal.  En este artículo, los autores introdujeron un nuevo concepto de dimensión fractal (Fractal Dimension), el cual llamaron método FD por sus siglas en inglés, evaluando el comportamiento y la confiabilidad de series de tiempo con diferentes longitudes utilizando simulaciones de Monte Carlo.  Por otra parte, Kristoufek & Vosvrda (2013) introdujeron una nueva medida para la eficiencia de mercados, considerando la estructura de la correlación de los retornos y el comportamiento local de los inversores.  En un trabajo posterior Kristoufek & Vosvrda (2014) utilizaron la memoria a largo plazo, la dimensión fractal y la entropía aproximada, como variables de entrada para medir la eficiencia.  De esta manera, lograron revisar sobre la eficiencia del mercado de valores después de controlar los diferentes tipos de ineficiencias.  Aplicando el análisis del exponente de Hurst, la dimensión fractal y la entropía aproximada en 38 índices de todo el mundo, encontraron que los mercados más eficientes se encuentran en la Eurozona (Países Bajos, Francia y Alemania) y las menos eficientes en América Latina (Venezuela y Chile).  Manahov y Hudson (2014) por su parte, desarrollaron mercados de acciones artificiales o ficticios, utilizando plataformas en donde los usuarios pueden simular la compra y venta de acciones.  Con toda la información recaudada, utilizaron una serie de técnicas econométricas para analizar las propiedades emergentes de los mercados de capitales.  Analizaron la evolución histórica de tres índices: FTSE 100, S&P 500 y Russell 3000.  Encontraron que la heterogeneidad es una característica básica de un mercado eficiente y que la eficiencia de mercados no se basa necesariamente en el supuesto de racionalidad.  Señalaron también, que los mercados de acciones no muestran un comportamiento lineal, sino que muestran un proceso evolutivo más relacionado con la Hipótesis de Mercado Adaptado, debido a que las diferentes poblaciones de inversores existentes presentan diferentes sistemas de adaptación al mercado a lo largo del tiempo.  Así mismo, para garantizar la eficiencia, estos autores aconsejan la participación del gobierno con ciertas regulaciones en el mercado de capitales.

Por otro lado, Duarte y Mascareñas (2014) comprobaron la eficiencia débil en los 5 principales mercados bursátiles de Latinoamérica, usando 2 enfoques.  Primero evaluaron la normalidad de las series mediante las estadísticas básicas, el test Jarque-Bera y la prueba de bondad de ajuste de la chi-cuadrado.  En segundo lugar, contrastaron la caminata aleatoria de los activos en sus versiones RW1 (test Rachas y test BDS), RW2 (filtros de Alexander con algoritmos genéticos) y RW3 (Test Ljung-Box e Intervalo de Bartlett).  Encontrando que las 5 principales economías latinoamericanas han experimentado un cambio de no eficiencia a eficiencia en los últimos años de acuerdo con el siguiente orden cronológico: México (2007), Brasil (2008), Colombia (2008), Chile (2011) y Perú (2012).

Kumar & Bandi (2015) mencionaron en su trabajo que cada inversionista se comporta diferente bajo los diferentes horizontes de tiempo en que operan, el estudio se basó en el análisis desde 1999 al 2013, de dos principales índices de la India: BSE SENSEX y NSE NIFTY.  Dentro del período analizado incluye la caída de las punto.com, la crisis mundial del 2008, así como dos elecciones en la India.  Durante esta época de crisis, el comportamiento del mercado marcó mayor actividad entre todas las escalas de tiempo, según lo propuesto por la FMH.  Entre los resultados encontraron que la equidad de mercados en la India está influenciada posiblemente por las turbulencias políticas internas y las crisis financieras en mercados internacionales.  Así mismo, consideran que el comportamiento de los inversores durante eventos extremos impacta en la eficiencia de los mercados.  Barna et al. (2016) [3] propusieron la hipótesis de los mercados fractales, como alternativa para superar los límites de la EMH.  El autor considera que la FMH provee explicaciones interesantes de varios tipos de imperfecciones de mercado, como los efectos de las llamadas “colas gordas” o “fat tail”, volatilidad estocástica y la autosimilitud.  En este artículo, se encontró que los mercados emergentes de Europa y Asia están más cerca del estatus de "no persistencia" mientras que los mercados de América Latina exhiben signos más significativos de persistencia local, es decir, que los mercados latinoamericanos muestran fuertes autocorrelaciones positivas para el período analizado.

Linton y Smetanina (2016) plantearon una alternativa para medir la predictibilidad de los precios de las acciones.  Su trabajo se basa en los rendimientos reales en lugar de los rendimientos logarítmicos, asegurando que es la metodología más adecuada para obtener la predictibilidad del precio.  De esta manera, captura no solo la dependencia lineal, como el test de ratio de varianzas de Lo y MacKinlay (1988), sino también algunas dependencias no lineales.  Los autores derivan la distribución asintótica de los estadísticos bajo la hipótesis nula que los simples rendimientos brutos son impredecibles después de un ajuste medio constante.  Aplicando su metodología para diferentes series financieras, no encontraron evidencia contra la hipótesis de la martingala en horizontes cortos, sin embargo, la nulidad de la predictibilidad media se rechaza en horizontes más largos (K>80 días).  También compararon su prueba con el comúnmente utilizado test de ratio de varianzas y muestra que, aplicando a la misma media de datos y las estadísticas de ratio de varianzas, los test pueden ofrecer diferentes resultados.

Continuando con sus investigaciones Ferreira et al. (2017) examinaron el co-movimiento o “movimiento correlacionado” del mercado de valores utilizando cointegración, pruebas de causalidad de Granger y enfoques no lineales en el contexto de la información mutua y correlaciones.  Aplicaron Análisis adaptado Multifractal de Fluctuaciones sin tendencia (AMF-DFA) y Análisis adaptado Multifractal de correlaciones cruzadas sin tendencia (AMF-DXA).  Encontrando solo 170 pares de mercados de acciones cointegrados y de acuerdo con la causalidad de Granger y la información mutua, lograron notar que las relaciones más fuertes se encuentran entre los mercados emergentes, y entre los emergentes y mercados fronterizos.

Gil, Ávila & Ortiz (2017) basándose en el trabajo de Lo (2011) introducen el concepto de adaptación para comprender la eficiencia en los mercados financieros.  Considera que algunos antecedentes teóricos muestran la necesidad y pertinencia del análisis adaptativo como respuesta al paradigma tradicional enfocado en los planteamientos de la hipótesis de los mercados eficientes.  En particular expone dos críticas a la EMH: una desde la racionalidad del agente, que muestra la imposibilidad de la existencia de mercados eficientes a escala informacional, y otra desde la economía conductual, enfocada en la heterogeneidad de los agentes y la racionalidad limitada de aquellos.  Argumenta que, el planteamiento principal de la AMH muestra a la eficiencia de los mercados financieros no como una característica presente o ausente, sino como una cualidad que varía acorde con las condiciones del mercado, las cuales son determinadas por las intenciones entre sus agentes.  El autor menciona que, el principal postulado de la AMH radica en que la eficiencia del mercado depende de sus condiciones; es decir, es resultado de las interacciones de sus agentes.  Señala también que, la AMH permite explicar fenómenos como el comportamiento de rebaño o manada, que genera grandes caídas, aparentemente espontáneas, de los precios de los activos.  De igual manera, agrega que el agente contemplado en la AMH es un agente con racionalidad limitada, es decir, susceptible de cometer errores sistemáticos generados por procesos heurísticos o sesgos cognitivos.  Gil et al. (2017) concluyeron que la AMH contempla diferentes tipos de agentes que estarían en capacidad de: crear expectativas diversas con la misma información, tener diferentes grados de aversión al riesgo, cometer errores sistemáticamente, pero con el fin de sobrevivir en el mercado; y usar la innovación como herramienta principal para lograr su fin último de permanencia en el mercado.

A autores como Ramos, Trinidad & Sánchez (2017) les parece interesante el pair trading o estrategias de trading sobre pares de activos, porque consideran que es una prueba contra la EMH, puntualizan que bajo un mercado eficiente estas estrategias de negociación no funcionan en ningún caso.

El método del exponente de Hurst fue desarrollado originalmente para estudios hidrológicos.  Harold Edwin Hurst (1951), como Director General del Departamento de Física, era responsable, entre otras cosas, del estudio de las propiedades hidrológicas de la cuenca del Nilo, por lo que se encargó de idear un método de control del agua tomando una visión holística de la cuenca del Nilo.  Un valor H en el rango de 0, 5−1 indica una serie de tiempo con autocorrelación positiva a largo plazo, lo que significa que un valor alto en la serie probablemente será seguido por otro alto valor y que los valores durante un periodo de tiempo tenderán a ser altos.  Un valor en el rango 0−0, 5 indica una serie de tiempo con conmutación a largo plazo entre valores altos y bajos en pares adyacentes, lo que significa que un único valor alto probablemente será seguido por un valor bajo y que el valor después tenderá a ser alto.

Tabla 1
Interpretación Coeficiente Hurst

Dentro de las diferentes metodologías desarrolladas para obtener un valor numérico de este exponente, la más popular es el análisis R/S, desarrollado por Mandelbrot & Wallis en 1969.  No obstante, y prácticamente ya, desde su nacimiento autores como Lo (1989), y más recientemente autores como Weron (2002) o Sánchez et al. (2008), han puesto de manifiesto que el valor resultante para el exponente cuando la longitud de la serie temporal es demasiado corta está muy lejos de ser el adecuado, acentuándose el problema en el caso de series financieras.  Por ello, una de las líneas de investigación clásica consiste en el depurado y mejora de las técnicas de estimación del exponente de Hurst, ya sea mejorando el análisis R/S como lo mencionan, Lo (1989) y Weron (2002) o mediante el desarrollo de metodologías nuevas.  Podemos citar el Método Semiparamétrico de Hudaks (GPH) propuesto por Geweke & Porther-Judak (1983), el análisis Quasi Máximo Verosimilitud (QML) desarrollado por Haslett & Raftery (1989), el exponente de Hurst Generalizado (GHE) analizado por Barabasi & Vicsek (1991), el método del Periodograma según Taqqu, Teverovsky & Willinger (1995).  La metodología wavelets, como lo indica Veitch & Abry (1999), el método de la media móvil centrada (CMA) planteada por Alessio, Carbone, Castelli & Frappietro (2002), las metodologías MF-DFA observada por Kantelhardt, Zschiegner, Koscielny-Bude, Havlin, Bunde & Stanley (2002).  El exponente de Lyadpunov como lo señala Bensaïda (2014) y Das & Das (2006), los métodos basados en procedimientos geométricos (GM) como afirma Sánchez et al. (2012), y más recientemente el algoritmo de dimensión fractal (FD) como expresa Fernández, Sánchez & Trinidad (2013).

2.1. Algoritmos FD

3. Resultados

3.1. Brasil

El índice Bovespa es el indicador más importante del mercado de acciones de Brasil. Su importancia viene explicada por el hecho de que el índice refleja el comportamiento de los principales valores negociados en la Bolsa de Valores de Sao Paolo.  Este índice bursátil representa el valor actual de una cartera teórica de acciones constituida con un valor base de 100 puntos el 2 de enero de 1968.  Por tanto, el Ibovespa refleja tanto las variaciones de los precios de las acciones, como la repercusión de la distribución de los rendimientos. Su finalidad principal, es la de servir como indicador medio del comportamiento del mercado.

Figure 1
Evolución H para el período

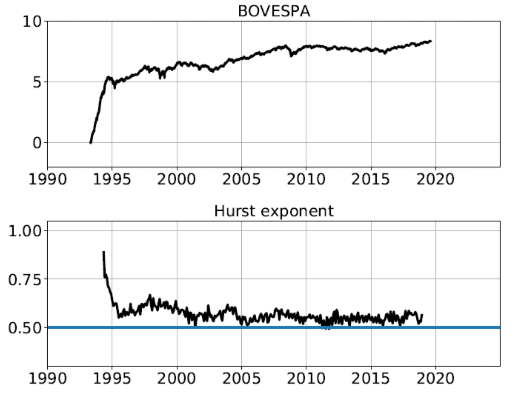
Puede observarse como hasta 2005 el valor deH está muy por encima de 0,5, mostrando una fuerte persistencia.  A partir de ese periodo se sitúa en valores próximos a un movimiento browniano e incluso llega a mostrar antipersistencia, lo que representa una clara mejora en la eficiencia del mercado.

3.2. Perú

El índice S&P/BVL Peru General está diseñado para ser el referente (benchmark) amplio del mercado peruano reflejando la tendencia promedio de las principales acciones cotizadas en Bolsa.  El S&P/BVL Peru General sigue la historia del antiguo IGBVL, manteniendo la base 30 de diciembre de 1991 = 100.  Sin embargo, a partir del 4 de octubre del 2015 es un índice de capitalización del free float.

Figura 2
Evolución H para el periodo

Del gráfico 2 se puede deducir de forma clara, que nos encontramos ante uno de los mercados latinoamericanos más ineficientes, con valores de H que casi alcanzan 0,75, lo que resulta muy extremo.  Tan sólo en momentos muy concretos el mercado llega a valores de 0,5.

3.3. México

El cálculo del índice IPC MEXICO viene determinado por la junta directiva de la Bolsa Mexicana de Valores, y puede cambiar cada trimestre o año, dependiendo de sus decisiones.

Figura 3
Evolución H para el periodo

La gráfica 3 muestra un comportamiento que guarda cierta similitud con el caso de Brasil, si bien la ineficiencia del mercado es más acentuada.  El exponente de Hurst muestra una elevada volatilidad, con valores muy por encima de 0,5, llegando a alcanzar valores superiores a 0,65, y otros periodos de mercado con una marcado antipersistencia.  La memoria a largo plazo es clara desde la creación del mercado hasta prácticamente el año 2015, fecha en la que se inicia una fuerte antipersistencia.

3.4. Argentina

El índice Merval refleja el valor de mercado de una cartera de acciones, seleccionada de acuerdo a la participación, cantidad de transacciones y valor de cotización en la Bolsa de Comercio de Buenos Aires.  El índice se computa continuamente durante la jornada de transacciones y se exhibe en las pantallas del Sistema de Información Bursátil.

Figura 4
Evolución H para el período

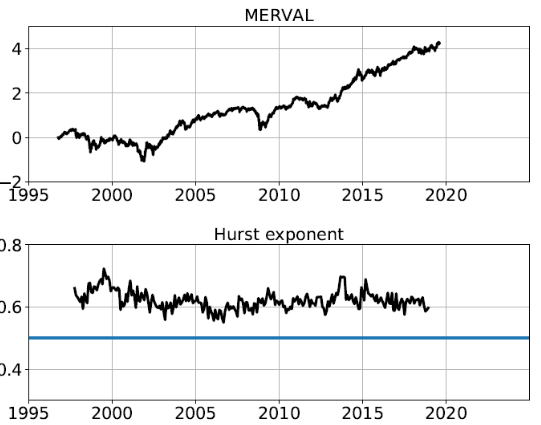
El gráfico 4 contiene el comportamiento del índice, así como el exponente de Hurst dinámico tal y como se ha mostrado en los casos anteriormente analizados.  En este caso, a diferencia de los anteriores, existe una memoria a largo plazo que se puede observar en todo el periodo estudiado.  En los gráficos se puede apreciar como H mantiene igualmente un comportamiento lateral muy claro sin que haya indicios, en ningún caso, que nos hagan suponer que hay una mejora en la eficiencia del mercado.

3.5. Chile

El índice IPSA es considerado el mejor indicador de rentabilidad del mercado de Chile. El IPSA se calcula mediante el promedio ponderado de las transacciones de las acciones de la cartera del índice, su finalidad es valorar las variaciones de precio de los títulos más líquidos del mercado.

Figura 5
Evolución H para el periodo

En la gráfica 5 se puede ver dos periodos claramente diferenciados en lo que al comportamiento del H se refiere.  Un primer periodo que abarca desde 2002 a 2013 marcado por una fuerte memoria a largo plazo y una volatilidad muy elevada, con valores de H que oscilan entre 0,65 y 0,5.  En el año 2013 se inicia una fuerte caía de la memoria hasta niveles de antipersistencia, manteniendo H estabilizado en valores próximos a 0,5 hasta 2016, fecha en la que se vuelve a disparar la memoria.

De la aplicación práctica se puede concluir que, en el caso de Brasil, hasta el 2005 el mercado muestra una fuerte persistencia, para posteriormente pasar a una clara antipersistencia, lo que representa una mejora en la eficiencia en comparación con el resto de mercados estudiados, si bien no podemos concluir de ninguna forma que el mercado sea eficiente.  Es importante resaltar que este intervalo de tiempo está caracterizado por ser el periodo pre-crisis de las hipotecas subprime.  Por otro lado, Perú es uno de los mercados latinoamericanos más ineficientes, con valores de H que casi alcanzan 0,75.  La memoria a largo plazo de México es clara desde la creación del mercado hasta prácticamente el año 2015, fecha en la que se inicia una fuerte antipersistencia.  En Argentina existe una memoria a largo plazo que se puede observar en todo el periodo estudiado.  Se apreció como H mantiene un comportamiento lateral muy claro sin que haya indicios, en ningún caso, que nos hagan suponer que hay una mejora en la eficiencia del mercado.  En el caso de Chile, se observaron dos periodos claramente diferenciados en lo que al comportamiento del H se refiere. Un primer periodo que abarca desde 2002 a 2013, marcado por una fuerte memoria a largo plazo y una volatilidad muy elevada.  En el año 2013 se inicia una fuerte caída de la memoria hasta niveles de antipersistencia, manteniendo H estabilizado en valores próximos a 0,5 hasta 2016, fecha en la que se vuelve a disparar la memoria.

Los resultados obtenidos están en la línea de la hipótesis del mercado fractal, con movimientos que van desde una acentuada persistencia a momentos de ligera persistencia.  Los responsables del comportamiento de estos mercados posiblemente sean, por una parte, el aumento en la capitalización de estos mercados, debido al crecimiento de la inversión directa extranjera a partir del 2007, motivado por las inversiones en infraestructura y explotación de materias primas por parte de países como Estados Unidos, Holanda, China, Canadá y España.  Por otra parte, pero relacionada con la anterior, por la movilización de capitales desde las economías desarrolladas hacia mercados emergentes, como consecuencia de la crisis económica originada en los Estados Unidos en noviembre del 2007.  Estos resultados, que van en la línea de los que presentan Duarte y Mascareñas (2014), son una primera aproximación a un estudio que debe de profundizar en otros aspectos tales como el estudio de los patrones de multifractalidad de los distintos mercados, el análisis de H dinámico y la extensión del estudio de H de forma individualizada para los principales valores de cada mercado.

MASG y JETS agradecen la ayuda del Ministerio Español de Ciencia, Innovación y Universidades y FEDER, ref. PGC2018-101555-B-I00. MASG también agradece la ayuda del CDTIME. JETS agradece la ayuda del Ministerio Español de Economía y Competitividad, ref. DER2016-76053-R (MINECO/FEDER, UE).

Financial support from the Spanish Ministerio de Ciencia, through project PGC2018-101555-B-I00 is acknowledged. We also acknowledge the support of UAL-FEDER through project UAL18-FQM-B038-A.

Alessio, E.; Carbone, A.; Castelli, G. & Frappietro, V. (2002). Second-order moving average and scaling of stochastic time series. The European Physical Journal B-Condensed Matter and Complex Systems. Vol. 27, no 2, 197-200.

Barabasi, A. & Vicsek, T.  (1991).  Multifractality of self-affine fractals. Physical Review A. Vol. 44, no 4, 2730.

Barna, F.; Stefana, M. & Pasca, L. (2016). Fractal Market Hypothesis: The Emergent Financial Markets Case.  Economic Computation and Economic Cybernetics Studies and Research.  Vol. 50, 137-150.

Bensaïda, A. (2014). Noisy chaos in intraday financial data: Evidence from the American index.  Applied Mathematics and Computation.  Vol. 226, 258-265.

Bentes, S.; Menezes, R. & Mendes, D. (2008). Long memory and volatility clustering: Is the empirical evidence consistent across stock markets? Physica A: Statistical Mechanics and its Applications.  Vol. 387, 3826-3830.

Cajueiro, D. & Tabak, B. (2005). Ranking efficiency for emerging equity markets II. Chaos, Solitons and Fractals.  Vol. 23, 671-675.

Calvet, L. & Fisher, A. (2008). Multifractal volatility: theory, forecasting, and pricing.  Academic Press.

Das, A. & Das, P. (2006). Does composite index of NYSE represent chaos in the long-time scale? Applied mathematics and computation.  Vol. 174, no 1, 483-48.

Di Matteo, D.; Aste, A. & Dacorogna, A. (2005). Long-term memories of developed and emerging markets: Using the scaling analysis to characterize their stage of development. Journal of Banking & Finance.  Vol. 29, 827-851.

Duarte, J. y Mascareñas, J. (2014). Comprobación de la eficiencia débil en los principales mercados financieros latinoamericanos.  Estudios Gerenciales.  Vol. 30, 365-375.

Fama, E. (1970). Efficient capital markets: A review of theory and empirical work. The journal of Financial.  Vol. 25, 383-417.

Fama, E. (1965). The behavior of stock-market prices.  The Journal of Business.  Vol. 38, 34-105.

Fernández, M. & Sánchez, M. (2012). Fractal dimension for fractal structures: A Hausdor approach.  Topology and its Applications.  vol. 159, no 7, 1825-1837.

Fernández, M.; Sánchez, M.; Trinidad, J. & Roman. I. (2014). An accurate algorithm to calculate the Hurst exponent of self-similar processes.  Physics Letters A. Vol. 378, 2355-2362.

Fernández, M.; Sánchez, M. & Trinidad, J. (2013). Measuring the self-similarity exponent in Lévy stable processes of financial time series. Physica A: Statistical Mechanics and its Applications.  Vol. 392, no 21, 5330-5345.

Ferreira, P.; Dionisio, A. & Movahed, S. M. S. (2017). Assessment of 48 Stock markets using adaptive multifractal approach. Physica A: Statistical Mechanics and its Applications.  Vol. 486, 730-750.

Fifield, S. & Jetty, J. (2008). Further evidence on the efficiency of the Chinese stock markets: A note.  Research in International Business and Finance.  Vol. 22(3), 351-361.

Geweke, J. & Porther-Judak, S. (1983). The estimation and application of long memory time series models. Journal of time series analysis.  Vol. 4, no, 4, 221-238.

Gil, M.; Ávila P. & Ortiz, A. (2017). Financial markets, efficiency and adaptation.

Haslett, J. & Raftery, A. (1989). Space-time modelling with long-memory dependence: Assessing Irelands wind power resource. Journal of the Royal Statistical Society: Series C (Applied Statistics).  Vol. 38, no 1, p. 1-21.

Hurst, H. (1951). Long-term storage capacity of reservoirs.  Trans. Amer. Soc. Civil Eng.  Vol. 116, 770-808.

Kantelhardt, J.; Zschiegner, S.; Koscielny-Bude, E.; Havlin, S.; Bunde, A. & Stanley, H. (2002). Multifractal detrended fluctuation analysis of nonstationary time series. Physica A: Statistical Mechanics and its Applications.  Vol. 316, no 1, 87-114.

Kristoufek, L. (2012). Fractal markets hypothesis and the global financial crisis: Scaling, investment horizons and liquidity. Advances in Complex Systems.  Vol. 15.

Kristoufek L. & Vosvrda M. (2013). Measuring capital market efficiency: Global and local correlations structure.  Physica A: Statistical Mechanics and its Applications.  Vol. 392, 184-193.

Kristoufek L. & Vosvrda M. (2014). Measuring capital market efficiency: long-term memory, fractal dimension and approximate entropy.  The European Physical Journal B.  Vol. 87, 162.

Kumar A. & Bandi K. (2015). Explaining financial crisis by fractal market hypothesis: Evidences from Indian Equity Markets.  Hyperion International Journal of Econophysics. New Economy.  Vol. 8.

Lim K. (2007). Ranking market efficiency for stock markets: A nonlinear perspective.  Physica A: Statistical Mechanics and its Applications.  Vol. 376, 445-454

Linton, O. & Smetanina, E. (2016). Testing the martingale hypothesis for gross returns. Journal of Empirical Finance.  Vol. 38, 664-689.

Lima, E. J. & Tabak, B. M. (2005). Testing the random walk hypothesis for emerging market exchange rates. In Banco Central de Brasil Working Paper.

Lo, A. (2012). Adaptive markets and the new world order (corrected May 2012). Financial Analysts Journal.  Vol. 68, 18-29.

Lo, A. (1989). Long-term memory in stock market prices.  National Bureau of Economic Research.

Lo, A. & MacKinlay, A. C. (1988). Stock market prices do not follow random walks: Evidence from a simple specification test. The review of financial studies.  Vol. 1(1), 41-66.

Lo, A. (2005). Reconciling efficient markets with behavioral finance: the adaptive markets hypothesis.  Journal of investment consulting.  Vol. 7, no 2, 21-44.

Manahov, V. & Hudson, R. (2014). A note on the relationship between market efficiency and adaptability–New evidence from artificial stock markets. Expert Systems with Applications.  Vol. 41, 7436-7454.

Mlambo, C. & Biekpe, N.  (2017).  The efficient market hypothesis: Evidence from ten African stock markets.  Investment Analysts Journal.  Volume 36 (66), 5-17.

Mandelbrot, B. & Wallis, J. (1969). Robustness of the rescaled range R/S in the measurement of noncyclic long run statistical dependence.  Water Resources Research, Vol. 5.5, 967-988.

Noakes M. & Rajaratnam K. (2016). Testing market efficiency on the Johannesburg Stock Ex- change using the overlapping serial test. Annals of Operations Research.  Vol. 243, 273-300.

Onali, E. & Goddard, J. (2011). Are European equity markets efficient? New evidence from fractal analysis. International Review of Financial Analysis.  Vol. 20, 59-67.

Peters, E. (1994). Fractal market analysis: applying chaos theory to investment and economics, John Wiley & Sons, Vol. 24.

Ramos, R.; Trinidad, S. & Sánchez, G. (2017). Introducing Hurst exponent in pair trading. Physica A: statistical mechanics and its applications.  Vol. 488, 39-45.

Rényi, A. (1961). On measures of entropy and information.  In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Contributions to the Theory of Statistics. The Regents of the University of California.

Roberts, H. (1967). Statistical versus clinical prediction of the stock market.  Unpublished manuscript.

Sánchez, M.; Trinidad, J. & García, J. (2008). Some comments on Hurst exponent and the long memory processes on capital markets. Physica A: Statistical Mechanics and its Applications.  Vol. 387, no 22, 5543-5551.

Sánchez, M.; Fernández, M. & Trinidad, J. (2012). Introducing fractal dimension algorithms to calculate the Hurst exponent of financial time series. The European Physical Journal B.  Vol. 85, 86.

Shannon, CE. (1948). A Mathematical Theory of Communication. Bell System Technical Journal. Vol. 27, 379-423.

Squalli, J. (2006).  A non-parametric assessment of weak form efficiency in the UAE financial markets.  Applied Financial Economics.  Vol. 16, 1365:73.

Taqqu, M.; Teverovsky, V. & Willinger, W. (1995). Estimators for long-range dependence: an empirical study. Fractals.  Vol. 3, no 04, 785-798.

Tsallis, C.; Anteneodo, C.; Borland, L. & Osorio, R. (2003). Nonextensive statistical mechanics and economics. Physica A: Statistical Mechanics and its Applications.  Vol. 324, 89-100.

Veitch, D. & Abry, P. (1999). A wavelet-based joint estimator of the parameters of long-range dependence. IEEE Transactions on Information Theory.  Vol. 45, no 3, 878-897.

Weron, A. & Weron, R. (2000). Fractal market hypothesis and two power-laws. Chaos, Solitons & Fractals.  Vol. 11, 289-296.

Weron, R. (2002). Estimating long-range dependence: finite sample properties and confidence intervals. Physica A: Statistical Mechanics and its Applications.  Vol. 312, no 1, 285-299.

Zunino, L.; Zanin, M. & Tabak, B. (2010). Complexity-entropy causality plane: A useful approach to quantify the stock market inefficiency. Physica A: Statistical Mechanics and its Applications.  Vol. 389, 1891-1901.3  

Zunino, L.; Tabak, B.; Pérez, D.; Garavaglia, M. & Rosso, O. A. (2007). Inefficiency in Latin-American market indices. The European Physical Journal B.  Vol 60(1), 111-121.

1. Facultad de Ciencias Administrativas, Universidad de Guayaquil. karen.balladaresp@ug.edu.ec

2. Departamento de Economía y Empresa, Universidad de Almería. jetrini@ual.es

3. Departamento de Matemáticas, Universidad de Almería. misanche@ual.es