ISSN 0798 1015

Vol. 40 (Number 28) Year 2019. Page 4

A strategy based on the open traveling salesman problem to solve the vehicle routing problem with backhauls (Colombia)

Una estrategia basada en el problema del vendedor ambulante de calle para resolver el problema de ruta de vehículos con remolque

LONDOÑO, Julio C. 1; NARVAEZ, Lady T. 2; VASQUEZ, Stephania 3 & BRAVO, Juan J. 4

Received: 11/03/2019 • Approved: 08/08/2019 • Published 26/08/2019

Contents

1. Introduction

2. Methodology

3. Case study and results

4. Conclusions

Bibliographic references

1. Introduction

The problem of routing vehicles with pickups and deliveries (linehaul-backhaul) has been defined as a capacitated Vehicle routing problem (VRP) in which delivery points and collection points are involved, implying a backhaul process (Vehicle routing problem backhaul or VRPB), and this problem has a critical assumption which states that all deliveries must be made on each route before any collection can be made (Blecha and Goetschalckx, 1993; Ferdinand, Kim, Lee & Ko, 2012). This assumption is motivated by the fact that in many practical applications the delivery service has a higher priority (Thoth and Vigo, 1997). The problem being considered is to design a set of routes, one for each available vehicle, so that each client is visited exactly once and the sum of the costs of the route is minimized (Mingozzi et al., 1999). 

In the VRPB solution, several heuristic algorithms have been presented in Deif and Bodin (1988), Blecha and Goetschalckx (1993), Potvin et al., (1996), Thangiah et al., (1996), Anily (1996), Yano et al., (1997), Tavakkoli et al., (2006), among others. Also, it can be resolved as a traditional VRP by assigning first and routing later, which operates in two phases (Toth and Vigo, 2002), where the first phase seeks to generate groups of customers who will be on the same route and then, in the second phase, for each group a route is created. In the first phase, it can be used the Savings Method, a simple and practical heuristic used in many articles (e.g., Park & Yoon, 2012). The capacity constraints are considered in the first stage, ensuring that the total demand of each group does not exceed the capacity of the vehicle, and then, for each group the route is built, solving in each case a TSP-type problem (Traveling Salesman Problem) with backhaul (TSPB).

The TSPB can be considered as a special case of the VRPB, in which the capacity of the vehicle is greater than the maximum value of the total demand to be delivered or the total amount to be picked up, and only a single vehicle is available (Toth and Vigo, 2002; Süral et al., 2010). In addition, it can be treated as a special case of the Clustered Traveling Salesman Problem CTSP (Gendreau et al., 1996). Mladenović and Hansen indicate that in the TSPB, customers (or cities) are divided into three disjoint sets: deposit, linehaul customers “L” and backhaul clients “B” and that a route that starts in the deposit must be designed such that all linehaul clients are visited contiguously before all backhaul clients (Süral et al., 2010). For the TSPB, a specific mathematical formulation has not been presented, and the proposed solutions correspond to heuristics. In Aramgiatisiris (2004), a solution proposal to the TSPB is presented by means of decomposition algorithms.

In this article, a special case of VRPB is considered. This consists of a set of clients that receive products which are handled by means of returnable transport items or RTIs (e.g., plastic baskets, containers) (Yu, Wang & Ha, 2013). The RTIs are used to favor the conservation of products during the delivery process and also during the first internal handling at the client location. The last reason, combined with the fact that deliveries have a high priority, is why RTIs are left at the client location and picked up later. After a distribution process is totally done, the collection of RTIs can start with the same vehicle the same day, and this is so because RTIs must be available for using them in deliveries in the next period.

For the solution of the aforementioned problem, the two-phase heuristic which implies cluster-first and route-second is used. In the first phase, the clustering of clients is done through the Generalized Assignment method, and in the second phase, the TSPB was first solved by an adaptation of the formulation of the TSP done by Miller, Tucker and Zemlin as proposed in (Miller et al., 1960). Due to this solution strategy, the total number of nodes representing clients doubled (i.e., each client is at the same time a linehaul and a backhaul node), and the solution to this problem, with this modeling strategy, was only possible for very small instances. The solution to this situation was then focused on the consideration of TSPB as an Open Traveling Salesman Problem OTSP, which generates a route that is traversed twice, once, to make the deliveries and again, to make the pickups. The traditional OTSP determines the route that a vehicle must take from the deposit and visit once the total number of customers assigned to a route, traveling the minimum distance possible, without the need to return to the central warehouse or deposit. In the present article, we show that taking the OTSP solution, starting from the last visited client in the delivery process, we can start the RTIs pickup process, visiting each client again and going to the deposit using the same route obtained from the initial OTSP but in a backward strategy. We have called this version DOTSP, because of the double visit to the clients by the same OTSP route, with combined forward and backward schemes, and to the best of our knowledge, it has not been used to solve the routing problem with backhaul considerations.  In Čičková et al., (2013) and Faragó et al., (2015), the traditional OTSP was used where it is not required to return to the deposit after visiting the last client.

1.1. Problem statement

The problem faced in this paper is associated with the existence of a supplier that supplies a single product to multiple distributors, which are located geographically dispersed. The demand for the products responds to a replenishment policy established by the distributor, who places an order to the supplier, and therefore, the quantities to be delivered to the distributors are considered known. It is assumed that the supplier has sufficient capacity to meet the demands of the distributors, so, in this case, pending orders are not considered. For the distribution of products, the supplier has a homogeneous fleet of vehicles of limited capacity, and given the conditions for the handling of products, they are transported through RTIs, which belong to the supplier and are not part of the product that is being delivered. Considering also the availability of RTIs in the supplier, these handling devices must be collected and returned to the supplier on the same day of delivery. This problem has been inspired in the case of the food sector, where the supplier is a manufacturer that must apply all the rules related to good practices for the handling and distribution of their products. In particular, it should avoid cross-contamination as much as possible, so that the product does not have any contact with external elements of any kind that may be considered as polluting agents. Therefore, both the returns and the used RTIs cannot be collected until the transport vehicle is completely empty, that is, after all deliveries have been done. Considering this situation, the supplier must program the vehicles to make all deliveries to distributors and then schedule the collection of RTIs considering the capacity restrictions of the vehicles, as well as the fact that a customer must be assigned to exactly one vehicle, seeking to minimize the total cost associated with the total distance traveled.

The problem already mentioned is considered as the problem of vehicle route design with pickups and deliveries (VRPB), which has been defined as a non-directed graph G = (V, A) such that V = {0} U L U B, where L = {1, …, n} is the set of n linehaul clients to which a delivery must be made, B = {n+1, …, n+m} are the m backhaul clients to which a pickup process must be made, the vertex 0 corresponds to the deposit, and A = {(i, j) : i, j ∈ V, i ≠ j}. In this problem, the linehaul clients and the backhaul clients are the same and therefore n = m. A non-negative cost dij is associated with each arc (i, j) ∈ A, and a non-negative qi is associated with the demand of each client. A fleet of M vehicles of Q capacity is available in the warehouse that must be programmed to deliver and pick up.

The total cost of the route corresponds to the total sum of the arcs that form it. Figure 1 shows an example of the problem enunciated with a feasible solution addressed from the DOTSP.

Figure 1
An example of a solution to VRPB from the DOTSP

In this section we present a modeling proposal inspired by the well-known work done by Fisher and Jaikumar (1981), the Generalized Assignment method for VRP. The difference between the method proposed here and that of Fisher and Jaikumar consists of the presence of backhaul clients, which must be programmed once all the deliveries have been made, which makes it necessary to modify the way in which the sequence of visits must be performed. The proposed algorithm is designed in three phases: (1) determination of insertion costs, (2) assignment of clients to routes, and (3) determination of the sequence. In the phase of determination of insertion costs, seed points are established and represent the center of a trip made by each vehicle, which are obtained by dividing the total load to be shipped over the number of vehicles available to obtain a seed load Lseed. After that, by means of a sweep, it obtains cones with an assigned Lseed, locating the seed point s in the middle of the cone at a distance equal to the farthest client from the supplier within the cone with partial or total load.

The insertion cost Cik is assumed as the extra distance that would be traveled if the client is inserted into a trip from the supplier to the seed point and returns. This cost is given by Cik = d0i + dis – d0s, where d0i represents the distance from the supplier to the client i, dis the distance from the client i to the seed point s and d0s the distance from the supplier to the seed point s. In phase two, for the assignment of clients to routes, a knapsack problem [0, 1] is solved, in such a way that the total cost of insertion is minimized. This problem is formulated as a mathematical programming model and requires the definition of the following variables:

where ai represents the demand of client i and bk the capacity of vehicle k.

Equation (1) determines the objective function that minimizes the total cost of insertion, the equations (2) guarantee that any client i is assigned to a route, and equations (3) guarantee that capacity of the vehicle is not exceeded. In the third phase, the problem of determining stops for each route is solved. This problem is considered as a TSP or traveling salesman problem, but in this particular case, the problem is really a TSPB, considering backhauls. In the following section, we present the formulation and strategy used to solve the TSPB.

2.1. The TSPB model

The TSPB model presented is a variant of the formulation used by Miller, Tucker and Zemlin (1964), and we take this formulation and add the constraint that the visit to the backhaul locations only take place once all linehaul distributors have been visited and the vehicles are completely empty. The proposed formulation is presented below:

Equation (4) states that the objective function minimizes the total cost of the route, equations (5) to (8) impose arrival and departure restrictions on a single node in the network, and constraints (9) and (10) seek to eliminate subtours for linehaul and backhaul points of the network respectively. Finally, equations (11) delimit the integrality of the variables.

This section presents the implementation of the model in a company of the food sector, which manufactures and distributes bakery products. First the description and data of the case study is presented, and the results are presented later.

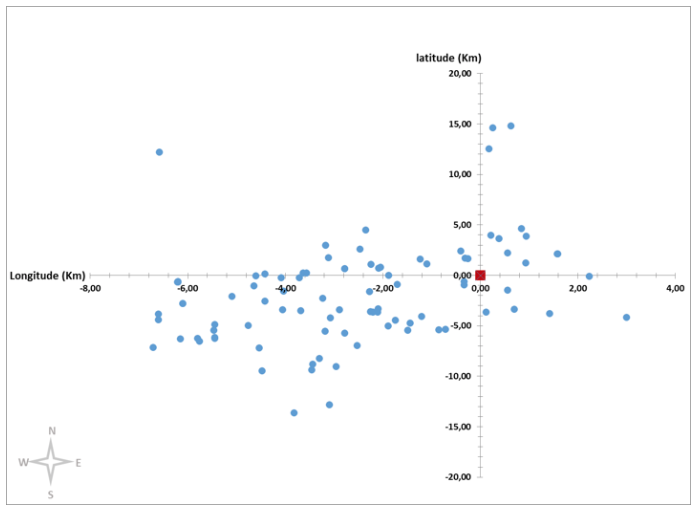
Description and data

The supply chain consists of a warehouse and 90 customers located geographically dispersed in the urban area where the company operates (see Figure 2). The bakery industry distributes breads. These products are characterized by their low density. Due to the particular characteristics of the product, it is transported in plastic baskets for protection (RTIs). The dimensions of the baskets are 60×40×13 cm. Given that the company uses a daily replenishment system based on the forecasts made by the marketing area, the quantities to be replenished at each distribution point are known. The distribution is made through a homogeneous fleet of five trucks with capacity of 312 baskets each. The coordinates of all nodes in the network in terms of latitude and longitude and the demands for a typical day are presented in Appendix A. The transportation cost is assumed to be proportional to the total distance traveled. It is assumed that once the product is delivered, the vehicle returns visiting all customers who were previously served, in order to recover the RTIs (in this case, baskets) used to transport the product.

Figure 2
Geographical representation
of the deposit and customers

3.1. Analysis and discussion

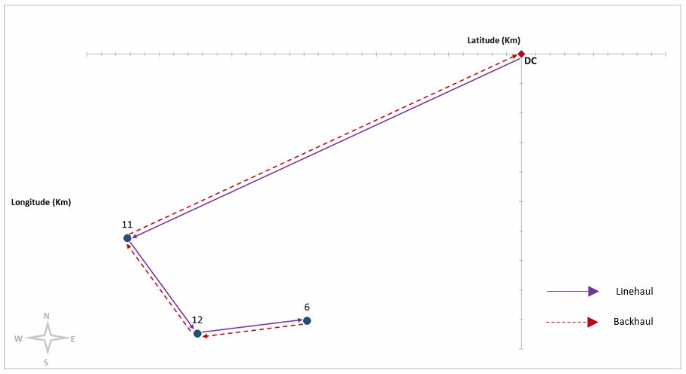
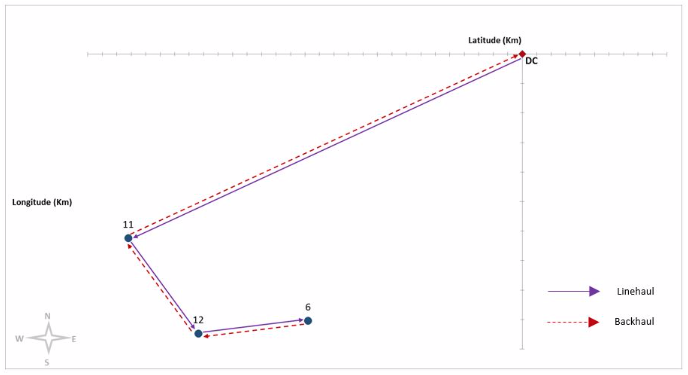
We apply the Generalized Assignment method to assign clients to each of the routes. The results are presented in Table 1. The model proposed for the TSPB was implemented to establish the sequence in which the clients will be visited both for the delivery of products and for the collection of RTIs in each route. The model was programmed in the AMPL language and was solved using the Gurobi solver. In this case, the model could only be applied to routes 2, 3 and 4, and because of computational capacity the sequence in which the clients are visited in routes 1 and 5 could not be performed. The sequence in which the clients are visited and the total distance travelled are presented in Table 2. Figure 3, Figure 4 and Figure 5 show the graphical representation of these routes.

Table 1
Assignment of clients to route
by generalized assignment

-----

Table 2
Sequence of visit and total distance travelled
for routes 2, 3 and 4 with TSPB

-----

Figure 3
Sequence of visit of the clients assigned to Route 2

-----

Figure 4
Sequence of visit of the clients assigned to Route 3

-----

Figure 5
Sequence of visits of customers assigned to Route 4

For route 1 with 28 assigned clients and route 5 with 38 clients, the number of nodes to be considered were 57 and 78 respectively, because of having to consider delivery and collection processes in the same day. This amount of nodes made the solution of the TSPB not possible. As a solution proposal, we applied a direct formulation of the OTSP for these two routes, which establishes the shortest distance of a tour that starts from the deposit and visits all the clients only once. In order to determine the return sequence, the same sequence used for deliveries is used but in a reverse scheme, implying a DOTSP. Next, the OTSP mathematical model is presented, where we add a new variable:

yi = Binary variable equal to 1 if client i is the last in the sequence, 0 otherwise

Equation (12) states that the objective function minimizes the total cost of the route, equations (13) impose exit restrictions on a single node in the network, except for the node that will be the last one in the tour, the equations (14) impose restrictions on arrival at a single node in the network, restrictions (15) are for elimination of subtours, equations (16) ensure that there is a single final node and, finally, equations (17) establish the condition that Xij and Yi are binary.

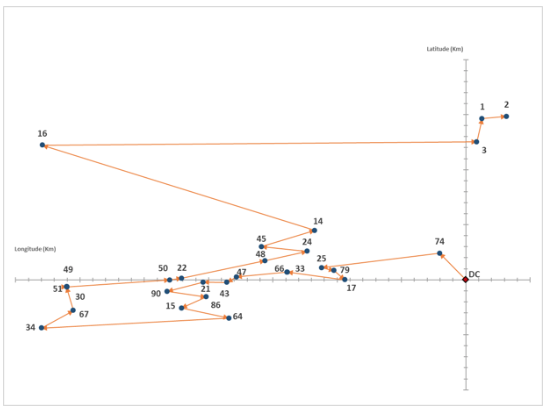
The model was formulated in the AMPL language and was solved by Gurobi. For routes 1 and 5, the results of the OTSP are shown in Table 3. The graphical representation of these routes is presented in Figure 6 and Figure 7.

Table 3
Sequence of visits and total distance
travelled for route 1 and 5 using OTSP

-----

Figure 6
Sequence of visits of linehaul
clients assigned to route 1

The complete tour is obtained by making the backhaul sequence in an identical way to the linehaul sequence, but in the opposite direction, and the length of the tour is obtained by multiplying by two the distance obtained for each route in the OTSP. Thus, for route 1 the distance traveled is 115 km, and for route 5 the distance traveled is 111.2 km. For verification purposes, this sequencing process with the DOTSP strategy was replicated to routes 2, 3 and 4, which had been resolved with the initial TSPB model. For these three routes, the results achieved with both types of modeling strategies were identical in terms of the total distance.

Figure 7
Sequence of visits of linehaul
clients assigned to route 5

1.  Benefits of integrating deliveries and RTI collection

As observed, the proposed model allows doing the process of product delivery and collection of RTIs in the same program. These results were compared with those obtained by the company where the RTI collection is not combined in the same route with the deliveries (or after them) but facing them as independent processes. To make the comparison, it was decided to take the five routes obtained through the Generalized Assignment procedure, establishing the sequence of deliveries by solving a TSP for each route. The results are presented in Table 4.

Table 4
Sequence of visits and total distance traveled
for routes 1,2,3,4, and 5 with TSP 

The total distance covered in the five routes in the delivery process is 228.3 km. Given that the company does this process twice, when making the same routes for pickups, the total distance traveled for delivery and collection is 456.6 km. This result was compared with the result of the routes proposed in the DOTSP strategy, which is 355.4 km. This allows us to calculate a savings of 101.2 km traveled for each occasion that all customers must be visited. This represents a savings of 22.16%.

In this article we present a proposal to integrate the activities of product delivery with the pick up of the returnable transport items (RTIs) traditionally used to handle products in the distribution process, characterized by multiple clients which are served by a homogeneous fleet of vehicles.

The proposed methodology was applied in a case study of a supply chain consisting of a deposit and 90 customers. In this work, an assign-first and sequence-later strategy was applied. The sequencing process offers a challenge when combining the delivery of products with the collection of RTIs. This process was initially carried out as a TSPB or Traveling Salesman Problem with Backhaul, but the computational time did not allow solving the model efficiently. This situation was faced by using an adaptation of the Open TSP, called Double OTSP, method that was able to solve the problem with satisfactory results. The experience showed that the results of TSPB and the Double OTSP (DOTSP) in terms of distances are identical, and therefore, the DOTSP allows to solve the TSPB.

Finally, the results in practice show that the decisions to integrate delivery with RTI’s pick up allow to obtain important savings in the total distance traveled. This problem can be extended to a situation in which companies must comply with restrictions related to the compliance of time windows.

Anily, S. (1996). The vehicle-routing problem with delivery and back-haul options. Naval Research Logistics, 43(3), 415–434.

Aramgiatisiris, T. (2004). An exact decomposition algorithm for the traveling salesman problem with backhauls. Journal of Research in Engineering and Technology, 1(2), 151–164.

Blecha, J., and Goetschalckx, M. (1993). The Vehicle Routing Problem with Backhauls: Properties and Solution Algorithms. Retrieved from: http://neo.lcc.uma.es/radi-aeb/WebVRP/data/articles/VRPB.pdf

Čičková, Z, Brezina, I., and Pekár, J. (2013). Open traveling salesman broblem with time wi, 1st Logistics International Conference (November), (pp. 28–31). Belgrade, Serbia.

Deif, I., and Bodin, L. (1988). Extensión of the Clark y Wrigth Algorithm for Solving the Vehicle Routing Problem with Backhauling. Management Sciences y Systems, 16, 65–84.

Faragó, C., Faragó, P., Hintea, S., and Oltean, G. (2015). An Evolutionary FPAA Reconfiguration Algorithm Based on the Open Traveling Salesman Problem, Acta Technica Napocensis. Electronica-Telecomunicatii, 56(1), 21–29.

Ferdinand, F.N., Kim, Y.J., Lee, H.K., and Ko, C.S. (2014). A study on collaborative pick-up and delivery routing problem of line-haul vehicles in express delivery services. International Journal of Industrial Engineering: Theory, Applications and Practice, 21(6), 376-383.

Fisher, M. L., and Jaikumar, R. (1981). A Generalizaded Assignment Heuristic For Vehicle Routing. Networks, 11, 109–124.

Gendreau, M., Hertz, A., and Laporte, G. (1996). The Traveling Salesman Problem with Backhauls. Computers & Operations Research, 23, 501–508.

Miller, C. E., Tucker, A. W., and Zemlin, R. A. (1960). Integer Programming Formulation of Traveling Salesman Problems. Journal of the ACM, 7(4), 326–329.

Mingozzi, A., Giorgi, S., and Baldacci, R. (1999). An Exact Method for the Vehicle Routing Problem with Backhauls. Transportation Science, 33(3), 315–329.

Park, Y.B., and Yoon, S. J. (1012). The operation of vending machine systems with stock-out-based, one-stage item substitution. International Journal of Industrial Engineering: Theory, Applications and Practice. 19(11), 412-427.

Potvin, J.-Y., Duhamel, C., and Guertin, F. (1996). A genetic algorithm for vehicle routing with backhauling. Applied Intelligence, 6(4), 345–355.

Süral, H., Özdemirel, N. E., Önder, I., and Turan, S. M. (2010). An Evolutionary Approach for the TSP and the TSP with Backhauls. In J. Tenne & C.-K. Goh (Eds.), Computational Intelligence in Expensive Optimization Problems (pp. 371–396). Springer Verlag.

Tavakkoli-Moghaddam, R., Saremi, A. R., and Ziaee, M. S. (2006). A memetic algorithm for a vehicle routing problem with backhauls. Applied Mathematics and Computation, 181(2), 1049–1060.

Thangiah, S. R., Potvin, J. Y., and Sun, T. (1996). Heuristic approaches to vehicle routing with backhauls and time windows. Computers and Operations Research, 23(11), 1043–1057.

Toth, P., and Vigo, D. (1997). An Exact Algorithm for the Vehicle Routing Problem with Backhauls. Transportation Science, 31(4), 372-385.

Toth, P., and Vigo, D. (2002). VRP with Time Windows. In P. Toth & D. Vigo (Eds.), The Vehicle Routing Problem (p. 367). Philadelfia: Society for Industrial and Applied Mathematics.

Yano, C. A., Chan, T. J., Richter, L. K., Cutler, T., MurtyK, G., and McGettigan, D. (1997). Vehicle Routing at Quality Stores. Interfaces, 2(2), 52–63.

Yun, W.Y., Wang, W.F., and Ha, B.H. (2013). A hybrid SA algorithm for inland container transportation. The International Journal of Industrial Engineering: Theory, Applications and Practice, 20(1-2), 12–23.

1. Escuela de Ingeniería Industrial, Universidad del Valle. julio.londono@correounivalle.edu.co

2. Universidad del Valle, Planning Department, leydy.narvaez@correounivalle.edu.co

3. Universidad del Valle, Planning Department, stephania.vasquez@correounivalle.edu.co

4. Escuela de Ingeniería Industrial, Universidad del Valle. Juan.bravo@correounivalle.edu.co