

Vol. 40 (Number 27) Year 2019. Page 14
MURILLO , Michel J. 1; GAVIRIA , Carlos A. 2; CANTILLO, Yamith A. 3 y ACOSTA, Carlos A. 4
Received: 25/11/2018 • Approved: 03/08/2019 • Published 05/08/2019
ABSTRACT: Changes in dynamic properties of structures, such as damping ratios and natural frequencies can be detected by periodic monitoring (e.g. one time by year). These changes are often indications of structural damage thereby, the maintenance or demolition of the structure can be doing in due time. In the case of pedestrian bridges, people’s movements may produce a resonance state, which leads to excessive deflection that accelerates the deterioration of these structures. Typically, these dynamic properties are detected by using high-cost vibration measurement equipment to achieve high levels of precision (i.e. a very low noise levels). This article studies the measurement of dynamic properties in pedestrian bridges using a tri-axial accelerometer integrated into a mobile phone as a low-cost and alternative practice. Accelerations were recorded on a steel pedestrian bridge (flexible) and on a post-tensioned concrete pedestrian bridge (rigid) located in Barranquilla City (Colombia). Vibrations were induced by a person (e.g., by jumping). Previous studies based on traditional measuring techniques show that two dominant frequencies in both types of bridges can be identified. However, in this study a reliable damping ratio could only be established for the steel bridge that it is associated with the flexibility and the low amplitude of the induced vibrations by a single pedestrian user. |
RESUMEN: Los cambios en las propiedades dinámicas de las estructuras, como las relaciones de amortiguamiento y las frecuencias naturales, se pueden detectar mediante monitoreos periódicos (por ejemplo, una vez por año). Estos cambios son a menudo indicaciones de daños estructurales, por lo que el mantenimiento o la demolición de la estructura puede realizarse a su debido tiempo. En el caso de los puentes peatonales, los movimientos de las personas pueden producir un estado de resonancia, lo que conduce a una desviación excesiva que acelera el deterioro de estas estructuras. Normalmente, estas propiedades dinámicas se detectan utilizando equipos de medición de vibraciones de alto costo para lograr altos niveles de precisión (es decir, niveles de ruido muy bajos). Este artículo estudia la medición de las propiedades dinámicas en puentes peatonales utilizando un acelerómetro tri-axial integrado en un teléfono móvil como una práctica alternativa y de bajo costo. Las aceleraciones se registraron en un puente peatonal de acero (flexible) y en un puente peatonal de hormigón pos-tensado (rígido) ubicado en la ciudad de Barranquilla (Colombia). Las vibraciones fueron inducidas por una persona (por ejemplo, saltando). Estudios previos que emplean técnicas de medición tradicionales muestran que se pueden identificar dos frecuencias dominantes en ambos tipos de puentes. Sin embargo, en este estudio, solo se pudo establecer una relación de amortiguación confiable para el puente de acero que está asociada con la flexibilidad y la baja amplitud de las vibraciones inducidas por un solo usuario peatonal. |
Smartphones are currently used in a wide range of applications for academic, communications or entertainment purposes. Researchers have incorporated devices such as accelerometers into mobile phones to collect acceleration data. For example, Yu-chin Tai et al. (2010) has used acceleration data from these devices to detect road anomalies and evaluate road quality. The results show that this smart mobile device detected anomalies with 78.5% accuracy. Similarly, Pothole Patrol (Eriksson et al, 2008) and TrafficSense and Nericell (Mohan et al, 2008) are designed systems that use a mobile phone’s GPS and an integrated accelerometer to monitor road surface conditions.
Other successful applications of this type include the Wireless Sensor Data Mining (WISDM) Project (Lockhart, 2011), which uses data mining methods on accelerometer data to predict what people are doing while they are carrying their phones, and the Trace Track, which is an escort system that traces the walking path of people to help find them in public places, using an accelerometer to minimize GPS and WiFi localization measurement errors. This escort system features an error factor drawn from a Gaussian distribution centered on 0 and standard deviation 0.15m (Ming, 2013).
Generally at the national level, during the process of any structural design tends to give priority only to the security criteria, leaving aside the limits of service and comfort. Structures such as gyms, pedestrian bridges, arenas, and stadia are vulnerable to vibrations that affect functionality during service conditions; therefore, it is important to analyze their behavior (Millán et al, 2017). In the case of pedestrian bridges, people’s movements may produce a resonance phenomenon, which leads to excessive deflection, which in turn tends to accelerate the deterioration of structures of this type. Likewise, these types of structures are more vulnerable to these vibrations due to the great lights that must cover and to the creation of new materials lighter and more flexible (Sánchez et al, 2010).
The dynamic characterization of civil structures allows validating numerical models and monitoring structural health by identifying variations in their modal properties. Such variations could indicate structural damages caused simply by the normal use of the structure during its operational life, which could be localized and quantified early (Rengifo et al, 2017). Within the benefits of structural health monitoring are the best under-standing of the in situ behavior of the structure, early detection of damages, guarantee of strength and serviceability of the structure, reduction of time out of service, better maintenance and strategies of resources al-location (Garita, 2015).
Normally, the variation of these dynamic properties are detected using high-cost vibration measurement equipment to achieve high levels of precision and very low noise levels. In turn, for example, systems with fiber optic sensors FBG (Fiber Bragg Grating) have allowed the implementation of strategies for the identification of damages at various levels (detection, location, typification, severity), alerting in advance about possible risk conditions of a bridge (Navarro-Henríquez, 2014).
Regarding the ability to detect vibrations, tri-axial accelerometers incorporated into mobile devices have demonstrated consistent sensitivity values with low variability coefficients ranging from 1.9% to 4.2% (Amick et al., 2013). Although the purpose of the current application is different from the above examples, it also helps demonstrate the variety of scientific uses that can be given to commercially available smart phones that are accessible to most people.
Research of this type carried out in Colombia has shown that mobile devices are a suitable option for Structural Health Monitoring of flexible structures such as pedestrian bridges in cities, showing good correlation with the parameters established in the literature (Castellanos et al., 2016). This offers a practical way to assess the current conditions of bridges and to evaluate the changes caused by environmental conditions and use.
This article presents the first findings of an experimental study using mobile devices to record vibrations in pedestrian bridges. The first two sections describe the selected bridges, the equipment and methodology used to generate the vibrations, and the way the collected information was processed. In Section 4 the data, frequencies and identified damping ratios are shown. The last section presents conclusions on the results obtained using this device.
In the first stage of this study, two (2) pedestrian bridges were selected in Barranquilla, Colombia. For the effects of comparison, it was decided to perform structural monitoring on one concrete bridge and one metal bridge. The first bridge is a two-track concrete bridge comprised by a 20-cm-thick reinforced concrete plank attached to a pre-stressed beam (Figure 1-a) and supported by three columns (one on each side and one in the middle). The second is a single-track bridge built on two metal trusses held by four columns (two on each side) and a walkway consisting of a concrete slab over an assisting deck (Figure 1-b). For both bridges, the access system consists of ramps on each side, which are structurally independent from the walkway.
Figure 1
Photos of the pedestrian bridges: concrete
bridge (right) and metal bridge (left).

Source: Authors. (Taken from Gaviria et al., 2017)
The methodology takes into consideration the types of tests that are normally performed in studies of this type (e.g. Ortiz et al. 2008; Franco et al. 2010; Sánchez et al. 2013). In these prior studies, the following tests were performed with the objective of finding the key dynamic properties of the bridges (frequencies and damping ratios), in which the pedestrians are main source of excitation:
Environmental Vibration: It consists in gathering acceleration information on the structure produced by the environment (e.g. vibration propagated through the bridge’s pillars or other types of “noise”) and normal traffic over the bridge (e.g. operating vibration, Villamizar et al. 2014). It should be noted that vibrations of this type are significantly lower than those produced in other types of tests, and are usually used to determine the structure’s dominant frequencies. For this test, acceleration data was collected for close to 20 minutes (Figure 2).
Vibration from an individual walking: This type of test records the vibration produced by the controlled crossing of one person walking synchronically over the bridge’s walkway (Figure 3).
Vibration from an individual jogging: As in the above test, acceleration data is recorded for a person jogging across the bridge (Figure 4).
Vibration induced by an individual running: For this test, an individual crosses the bridge running (Figure 5).
Vibration induced by an individual jumping: It consists in collecting data while an individual jumps on the walkway from a given height, with a frequency of 30 seconds (approximately 20 jumps), aimed at generating high impact factors on the structure. The jumps generate pulsations that trigger the structure’s dominant vertical natural frequencies (Figures 7-e and 8-e).
A MEMS-type (Micro Electromechanical Systems) tri-axial accelerometer was used by means of the application Accelerometer Monitor installed on two (2) different mobile phone devices. The first device was a Sam-sung Galaxy E5 - Model SM-E500M fitted with a K2HH accelerometer developed by ST Microelectronics with resolution of 0.038307227 m/sec2, which was set up at the midpoint along the bridge’s length. The sec-ond mobile phone device was a Motorola Moto G with an incorporated KX222 accelerometer (resolution of 0.009576807 m/sec2) manufactured by Kionix, which was set up at one-third of the bridge’s length. Both units were configured with a sampling frequency of 50 Hz.
The collected data were processed using the mathematical program Matlab. To establish the natural frequencies and damping ratios, the Fourier signal spectrum and the logarithmic decrement methods were used, respectively.
This section presents some of the measurements obtained (typical) for each type of induced vibration, and the analysis performed to find the dynamic properties.
Figure 2 displays the accelerations recorded for the environmental vibration test on the bridges. Consequently, the maximum accelerations shown in the figure are the peak values measured on the structure due to the non-controlled passing of pedestrians during the test. This implies that the measured accelerations depend on the amount of pedestrian traffic passing over the bridge. The recordings are similar for both bridges, though the metal bridge displays greater peaks associated with normal pedestrian traffic.
Figure 2
Typical recording of environmental vibration taken at the
midpoint of the concrete (left) and metal (right) bridges
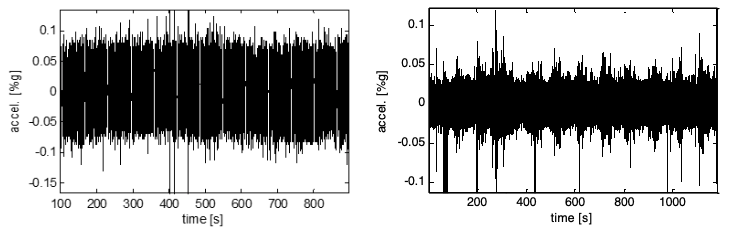
(Taken from Gaviria et al., 2017)
Figure 3 shows the change in acceleration in the vertical direction over time during walking. Even though the amplitude of the accelerations is similar for both bridges (~0.1g), the metal bridge, due to its greater flexibility, displays greater changes in the amplitude induced by walking.
Figure 3
Typical recording of vibration from walking taken at the
midpoint of the concrete (left) and metal (right) bridges

(Taken from Gaviria et al., 2017)
Figure 4 shows the recording of vibration induced by jogging. As was the case for walking, the metal bridge displays greater vibration amplitudes (~0.4g). However, in the concrete bridge there are no visible changes in vibration levels.
Figure 4
Typical recording of vibration from jogging taken at the
midpoint of the concrete (left) and metal (right) bridges

(Taken from Gaviria et al., 2017)
Figures 5 and 6 show recordings of vibrations induced by an individual running and jumping, respectively. In the case of the metal bridge, when compared to Figures 4 and 5, we observe that the vibrations from running display a band that is shorter in duration than that induced by jogging, as expected.
Figure 5
Typical recording of vibrations from running taken at
midpoint of the concrete (left) and metal (right) bridge

(Taken from Gaviria et al., 2017)
The recordings taken at one-third of the length are not displayed due to space considerations, but in general, the amplitude of the vibrations is lower due to the location of the device.
Figure 6
Typical recording of vibrations from jumping at the
midpoint of the concrete (left) and metal (right) bridges.
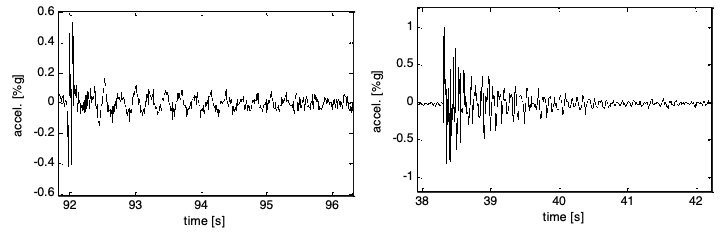
(Taken from Gaviria et al., 2017)
In Figure 6 we observe that the maximum accelerations of jumping-induced vibrations are the highest of all test results, due to the greater impact that jumping has on the point of greatest modal deflection, compared the other sources of excitation. The logarithmic decrement of accelerations is also more clearly defined on the metal bridge. In the case of the concrete bridge, the peak vibrations produced by jumping tend to vanish towards the middle of the chart, followed immediately by low-amplitude free vibrations (< 0.2g).
In general it is observed that recordings over time for the more flexible bridge (metal) offer clearer images of the vibrations induced by the different types of loads, which translates into more clearly defined frequencies and damping effects, as discussed below. On the other hand, the recordings of the different types of loads on the concrete bridge are all very similar and tend to look the same as the environmental vibration recording.
Below are the graphs generated for each test type, focusing only the behavior on the z axis. The Frequencies are identified using a Fourier transform (e.g. Aguirre et al., 2013) and the peaks are identified over the Fourier spectrums (Figures 7 and 8).
Figure 7
Fourier spectrum for the recordings of (a) environmental vibration, (b) walking,
(c) jogging, (d) running and (e) jumping at the midpoint of the concrete bridge

(Taken from Gaviria et al., 2017)
------
Figure 8
Fourier spectrum of the recordings of (a) environmental vibration, (b) walking,
(c) jogging, (d) run-ning and (e) jumping at the midpoint of the metal bridge
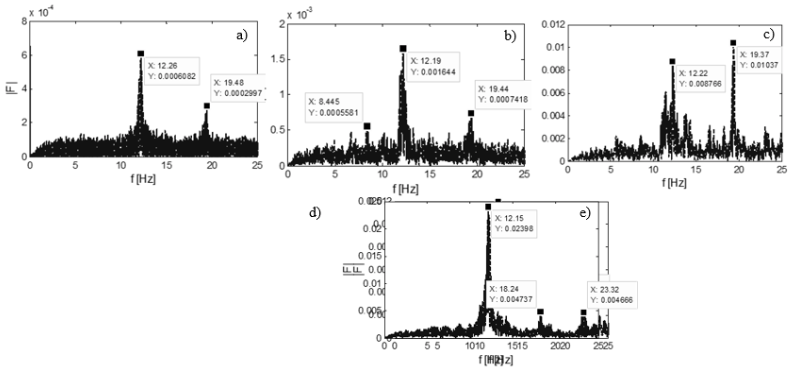
(Taken from Gaviria et al., 2017)
In the case of the concrete bridge (Figure 7), jumping and free vibration records clearly show two dominant frequencies on the bridge. Also, the vibrations recorded when running show a frequency of 2.751 Hz, which is consistent with frequencies reported for a person running (i.e. between 2.0 and 3.5 Hz, Bachmann and Ammann, 1987). On the metal bridge (Figure 8) two dominant frequencies are clearly observed for the different types of stimuli. Additionally, a third frequency was identified for jumping-induced vibration, and jogging contributes more to the second frequency identified than to the first (i.e. a higher peak in the spectrum of the second observed frequency).
Using the frequencies identified in Figure 7, as well as those obtained from the vibrations recorded at 1/3 of the length of the concrete bridge, we find that the first identified frequency is 4.42 ± 0.05 Hz and 4.19 ± 0.32 Hz for the recordings at 1/2 and at 1/3 of the length of the bridge, respectively. In other words, it displays percentage standard deviations of 1.13 and 7.64 %, respectively. Similarly, the metal bridge displays a natural frequency of 12.19 ± 0.05 Hz and 12.17 ± 0.08 Hz for the recordings at 1/2 and 1/3 of the length of the bridge, respectively. Therefore, the standard deviations are 0.41 and 0.66%, respectively.
Figure 9 shows an example of the calculated damping ratio for the first vertical frequency found using the free vibration recorded following an individual’s jump. The upper section displays a wavelet map, where the vertical dotted lines delimit the area from any borderline effects (i.e., the most reliable information range), the thick solid lines represent the “ridges” of the maximum values found, and the linearization of instantaneous amplitude (IA). For this process the method proposed by Gaviria and Montejo (2016) was used, i.e. the analytical signal is constructed from the Hilbert transform (Ramírez-Castro and Montejo, 2011), after performing modal decoupling using the transformed continuous wavelet with the recommended optimal parameters (Gaviria and Montejo, 2018).
The wavelet maps show that the maximum values for the metal bridge are located above the dominant frequency, which implies that the lineal instantaneous amplitude is within the reliability range. In contrast, the ridge found on the wavelet map for the concrete bridge displays high variation in frequency, creating oscillations in the instantaneous amplitude (thin gray line). Using the procedure shown in Figure 9, we find that the calculated damper ratio for the modality associated with the 4.42 Hz frequency is 0.0045 ± 0.0052 (i.e. per-cent standard deviations of 115%) using seventeen (17) records of jumps recorded at the midpoint of the concrete bridge. Similarly, the metal bridge displays a damping ratio of 0.0106 ± 0.0022 and 0.0097 ± 0.0017 for six (6) records of jumping recorded at the midpoint and at 1/3 of the length of the bridge, respectively. Consequently, the standard deviations are 21 and 18 %, respectively. This indicates that the damping results for the concrete bridge are unreliable, and this situation is associated with the low definition of the logarithmic decrement of the accelerations produced by one jump (Figure 6).
Figure 9
Wavelet map with the maximum values identified (top figures), and the respective logarithms
of instantaneous amplitude (bottom figures) for the concrete (left) and the metal (right) bridges

(Taken from Gaviria et al., 2017)
The mobile phones display consistent results in the identification of the first dominant frequency in the metal bridge at both accelerometer locations, with standard deviations of less than 1% for the various types of induced vibrations (environmental, walking, jogging, running and jumping). A similar result is found in the recordings at the midpoint of the concrete bridge (standard deviation of 1.13%). However, records at one-third of the length of the bridge display a standard deviation of 7.64%. It is important to highlight that in both the cases studied, the frequencies of the bridges are greater than the typical excitation frequencies (i.e. between 2.0 and 3.5 Hz, Bachmann and Ammann, 1987), which implies that they are clearly differentiated from the structure’s frequencies.
The damping values found for the concrete bridge display a very high standard deviation (greater than 100%), which is associated with the low amplitude of the vibrations induced by jumping. In the case of the metal bridge, the damping values are reliable for both mobile device locations (standard deviation of ~20%).
The greater quality of the dynamic properties measurements obtained for metal bridge is related to its greater dynamic sensitivity compared to the concrete bridge. The recordings of accelerations over time on the metal bridge consistently provide a clearer view of the vibration induced by the different types of loads. In contrast, the acceleration records over time for the concrete bridge do not differ substantially between types of loads, and they all tend to look similar to environmental vibration records.
The recordings from jumping (of a pulsation type) generate a clear Fourier spectrum that displays only the frequencies of the structure in the direction of the study, as is also the case for the environmental vibration recordings, and consequently these two types of stimuli are the ones that are recommended for the identification of dynamic properties using this type of mobile device.
It is recommended to increase the amplitude of the vibration on rigid bridges (concrete bridges) in order to in-crease the visibility of the variations in vibrations over time when a particular excitation is induced (e.g. jumping). For this a synchronized jumping or walking by a group of persons could be performed in order to increase the force of impact. It is also advisable to calibrate the devices using different types of stimuli (vibrating table, shaker or similar device), and comparing the readings to those of a high-precision seismic piezoelectric accelerometer.
Aguirre, D. A., Gaviria, C. A., & Montejo, L. A. (2013). Wavelet-based damage detection in reinforced concrete structures subjected to seismic excitations. Journal of Earthquake Engineering, 17(8), 1103-1125.
Amick R. Z., Patterson J. A., Jorgensen M. J. (2013). Sensitivity of Tri-Axial Accelerometers within Mobile Consumer Electronic Devices: A Pilot Study. International Journal of Applied Science and Technology, Volume 3, No. 2.
Bachmann H., Ammann W. (1987). Vibrations in Structures—Induced by Man and Machines, Structural Engineering Documents, Vol. 3e, International Association of Bridge and Structural Engineering (IABSE), Zurich.
Castellanos S., Marulanda J., Preciado M., Cruza A., Thomson P. (2016). Identification of the operational frequencies of 300+ bridges using Smartphones. Proc. of SPIE Vol. 9804. doi: 10.1117/12.2222097.
Eriksson J., Girod L., Hull B., Newton R., Madden S. and Balakrishnan H. (2008). The pothole patrol: using a mobile sensor network for road surface monitoring, in MobiSys’08: Proceeding of the 6th international conference on Mobile systems, applications, and services.
Franco, J. M., Ortiz, R. A., Gómez D. &Thomson P. (2010). Evaluación de las vibraciones producidas por las personas en el puente peatonal del Club Noel en Cali, Colombia. 21va Jornadas Argentinas de Ingeniería Estructural, 6-8 Octubre, Buenos Aires, Argentina.
Garita C. (2015). Enfoques de integración de información para sistemas de monitoreo de salud estructural de puentes. Tecnología en Marcha. Vol. 29, Nº 1, Enero-Marzo. Pág 96-107.
Gaviria, C.A., & Montejo, L.A. (2018). Optimal Wavelet Parameters for System Identification of Civil Engineering Structures. Earthquake Spectra, 34(1), 197-216.
Gaviria, C. A., & Montejo, L. A. (2016). Output-only identification of the modal and physical properties of structures using free vibration response. Earthquake Engineering and Engineering Vibration, 15(3), 575-589.
Gaviria C., Murillo M., Cantillo Y., Acosta A. (2017). VIII Conferencia Nacional de Ingeniería Sísmica, 8, 2017, Barranquilla, Colombia.
Gaviria, C. A., & Suarez L. (2015). Dynamic properties of a building with viscous dampers in non-proportional arrangement. Structural Engineering and Mechanics, Vol. 55 Iss. 6, p. 1241 – 1260, DOI: 10.12989/sem.2015.55.6.0000.
Lockhart J., Weiss G., Xue J, Gallagher S., Grosner A., and Pulickal T. (2011). “Design Considerations for the WISDM Smart Phone-based Sensor Mining Architecture, 1-9.
Millán D., Marulanda J. & Thomson P. (2017). Evaluación de la confiabilidad estructural de la Tribuna Sur del Estadio Pascual Guerrero, Cali. VIII Congreso Nacional de Ingeniería Sísmica organizado por la Universidad del Norte y la Asociación Colombiana de Ingeniería Sísmica.
Ming L. (2013). “A Study of Mobile Sensing Using Smartphones”, International Journal of Distributed Sensor Networks, 2013: 1-11, http://dx.doi.org/10.1155/2013/2729161-11.
Mohan P., Padmanabhan V., and Ramjee R. (2008). “Nericell - Using Mobile Smartphones forRich Monitoring of Road and Traffic Conditions,” Proceedings of the 6th International Conference on Embedded Networked Sensor Systems, DOI: 10.1145/1460412.1460444.
Navarro-Henríquez F. (2014). Sensores de fibra óptica FBG para el monitoreo de la salud estructural de los puentes. Tecnología en Marcha. Vol. 27, Nº 4, Octubre-Diciembre. Pág 3-13.
Ortiz, R. A., Gómez D. & Thomson P. (2008). Efecto De La Interacción Humano-Estructura En El Estadio Pascual Guerrero. 20va Jornadas Argentinas de Ingeniería Estructural, 15-17 Octubre, Buenos Aires, Argentina.
Ramírez-Castro, R. I., & Montejo, L. A. (2011). Transformada de Hilbert, descomposición modal empírica y sus aplicaciones en el análisis de vibraciones libres. Revista Internacional de Desastres Naturales, Accidentes e Infraestructura Civil, 11(2), 123-134.
Rengifo J., Rincón J., Franco J., Marulanda J. & Thomson P. (2017). Caracterización dinámica de estructuras con teléfonos móviles inteligentes. VIII Congreso Nacional de Ingeniería Sísmica organizado por la Universidad del Norte y la Asociación Colombiana de Ingeniería Sísmica.
Sánchez, J. A., Thomson, P., Gómez, D. & Ortiz A.R. (2010). Caracterización del efecto de la interacción humano-estructura en puentes peatonales de la ciudad de Cali. 21va Jornadas Argentinas de Ingeniería Estructural, 06-08 Octubre, Buenos Aires, Argentina.
Sánchez, J. A., Gómez, D., & Thomson, P. (2013). Análisis de la interacción humano-estructura en puentes peatonales de Santiago de Cali. Dyna, 80(177), 86-94.
Villamizar, S., Gómez, D., & Thomson, P. (2014). Efecto De Interacción Humano-Estructura En Losas. Dyna, 81(184), 129-137.
Yu-chin Tai, Cheng-wei Chan and Yung-jen Hsu. (2010). Automatic Road Anomaly Detection Using Smart Mobile Device. Procedia in Social and Behavioral Sciences.
1. Researcher Professor, Department of Civil and Environmental, Universidad de la Costa, Colombia. mmurillo4@cuc.edu.co
2. Researcher Professor, Distance teaching Faculty, Military University “Nueva Granada", Colombia. carlos.gaviria@unimilitar.edu.co
3. Researcher Professor, Department of Civil and Environmental, Universidad de la Costa, Colombia. ycantill6@cuc.edu.co
4. Civil Engineer, specialist in structures, graduate of Universidad del Norte, Colombia