

 Vol. 40 (Nº 26) Año 2019. Pág. 22
Vol. 40 (Nº 26) Año 2019. Pág. 22
AQUINO, Sócrates M. 1; ARIAS, Roberto F. 2; CORDOVA, Rafael A. 3 y ECHEVERRIA, Magdy M. 4
Recibido: 02/05/2019 • Aprobado: 12/07/2019 • Publicado 29/07/2019
RESUMEN: El trabajo muestra una práctica educativa para mejorar la comprensión de los estudiantes de dinámica de máquinas basados en la metodología de despliegue de la función de calidad. Se utilizaron herramientas para cálculo cinemático (ecuaciones homogéneas) y dinámico (método de trabajos virtuales y principio D´Alembert) mediante Matlab. Luego de realizar los cálculos de velocidades y aceleraciones, se comprobó la resistencia en los elementos críticos. Finalmente se construyó una maqueta del brazo de bajo costo con fines académicos. |
ABSTRACT: This research work shows an educational practice for improving of dynamics if machines for students by means of the quality function deployment. The tools for kinematic (homogeneous equations) and dynamic calculations (virtual work and D’Alembert methods) were applied using Matlab. After performing the velocity and acceleration calculations, the resistance in the critical elements was verified. Finally, a low-cost model of the arm (operated manually) was built for teaching purposes. |
Mecánicamente, un robot serial está formado por una serie de elementos o eslabones unidos mediante articulaciones que permiten un movimiento relativo entre cada dos eslabones consecutivos. La constitución física de la mayor parte de los robots industriales guarda cierta similitud con la anatomía del brazo humano, por lo que, en ocasiones para hacer referencia a los distintos elementos que componen el robot, se usan términos como cuerpo, brazo, codo y muñeca (Krar & Check, 2010). El movimiento de cada articulación puede ser de desplazamiento, de giro, o de una combinación de ambos. El estudio de la cinemática y dinámica de un robot son muy importantes, pues permiten determinar con certeza las posiciones, velocidades y fuerzas que se requieren para un funcionamiento adecuado. Robles, Román, y Polo (2016) realizaron el estudio de un prototipo de un brazo robot con 18 grados de libertad, operado a través de un guante electrónico que puede reconocer los movimientos realizados por el usuario, el resultado obtenido es bastante cercano a lo deseado, pues se simulan los movimientos ejecutados por el usuario.
Noguera, García, y Robles (2017) analizaron un robot manipulador utilizando las técnicas de control estándar y H infinito. Además, realizaron el análisis cinemático, dinámico del mecanismo exportando el modelo CAD de SolidWorks a Simulink. Los autores concluyen que el control H infinito es más efectivo en la respuesta transitoria; no obstante, no se hace énfasis en los métodos de resolución de los modelos cinemáticos y dinámicos. Roldán, Yime, y Sosa (2018) adaptaron un controlador de arquitectura a un robot con fines educativos, empleando servoamplificadores análogos de bajo costo integrados a una tarjeta de control dSpace, escogida por su facilidad de integración en los programas de Matlab y Simulink.
En base a los trabajos anteriormente mencionados, el presente trabajo de investigación muestra una práctica educativa para mejorar la comprensión de la dinámica de máquinas basados en la metodología de despliegue de la función de calidad para definir los criterios de diseño de un brazo robot para tareas de reciclaje. Se utilizaron las herramientas para cálculo cinemático inverso (ecuaciones homogéneas) y dinámico (método de trabajos virtuales) programados mediante Matlab. Se realizaron los cálculos de velocidades y aceleraciones, y se simuló la resistencia en los elementos críticos utilizando el software ANSYS. Finalmente se construyó una maqueta del brazo de bajo costo con fines académicos.
La función de calidad QFD se fundamenta en la búsqueda de las necesidades del usuario, teniendo en cuenta tanto las expresadas como las no expresadas, las cuales son trasladadas dentro de las acciones de diseño. Constituye una herramienta de apoyo importante para la toma de decisiones en la etapa temprana del diseño.
QFD se divide en 4 fases que son: planificación del producto, diseño del producto, desarrollo del producto y evaluación del desempeño. Cada una de estas fases utiliza una matriz para trasladar los requerimientos del cliente hacia los diferentes módulos de obtención del producto (López, 1997) (Ruiz, 1994). Al final del proceso de desarrollo, se obtendrá un producto totalmente adaptado a las necesidades del usuario.
Se utilizó una metodología para el diseño de productos, que permite realizar la traducción del mundo del cliente al mundo de la ejecución de un producto. Para la construcción de la matriz de la función de calidad QFD se utilizó una hoja de cálculo de libre distribución, en la cual se seleccionaron algunos parámetros deseados en este tipo de brazos robóticos.
La matriz construida se muestra en la figura 1, de donde se observa que los factores más importantes tienen que ver con el tipo de material de la máquina, su capacidad de ser producida y la aplicación de las normas para su modelación.
Figura 1
Matriz QFD para la construcción del brazo robótico

Existe una primera opción con tres grados de libertad, explotada comercialmente, con el nombre de Wall-B. Se apoya en la combinación de tecnología de visión por ordenador y robótica avanzada; este brazo robótico selecciona residuos plásticos que se encuentran en una cinta transportadora por medio de succión (Grupo LYRSA, 2016). Aunque cumple con algunas de las necesidades más importantes de la matriz QFD, su costo puede llegar a ser demasiado alto, y los tiempos de montaje muy elevados.
Tomando en cuenta los resultados de la matriz QFD, para la segunda opción, se ha realizado un modelo de un brazo robótico con 4 grados de libertad en SolidWorks como se muestra en la figura 2, que puede ser de cartón o de madera, con émbolos y pistones de baja potencia y que debido a los materiales con los que está diseñado, puede construirse en serie en grandes volúmenes; si se elaboran sus partes en primer lugar y luego se lo ensambla.
Figura 2
Opción elegida para el robot clasificador
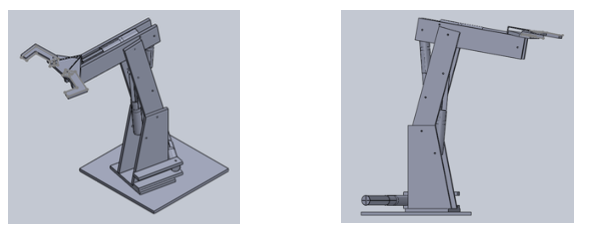
De esta manera se cumplirían los parámetros más importantes de la función de calidad, por lo que en el presente trabajo se utilizará esta opción por sobre la anterior. Cabe indicar que el modelo pretende ser utilizado con fines académicos, para impartir conocimientos sobre la dinámica de máquinas; el prototipo se muestra en la figura 3.
Figura 3
Prototipo armado

El rango de movimiento del extremo final (pinza) para el prototipo, se muestra en la tabla 1, tomando en cuenta que el sistema de referencia inercial se encuentra localizado en la base del mecanismo. Dado que la posición tridimensional deseada del mecanismo es lineal, se ha mantenido constante la posición en x; la posición de z se calcula utilizando la ecuación 1, mientras que la trayectoria final que recorrerá la pinza se muestra en la figura 6:
Tabla 1
Posiciones requeridas para el robot
Xi (m) |
Yi (m) |
Zi (m) |
Xf (m) |
Yf (m) |
Zf (m) |
0.32 |
0.09 |
0.09 |
0.32 |
-0.22 |
0.12 |
 (1)
(1)
El análisis cinemático se llevó a cabo mediante ecuaciones homogéneas, que luego fueron resueltas utilizando Matlab, la representación cinemática se muestra en la figura 5.
Donde:
zi,, representa la dirección de giro de cada elemento,
xi es perpendicular a zi
yi se obtiene mediante la regla de la mano derecha, haciendo girar z en la dirección de x.
qi, es el ángulo de giro de cada uno de los elementos del brazo
li, son las dimensiones geométricas
Figura 4
Posiciones y sistemas coordenados para el análisis cinemático
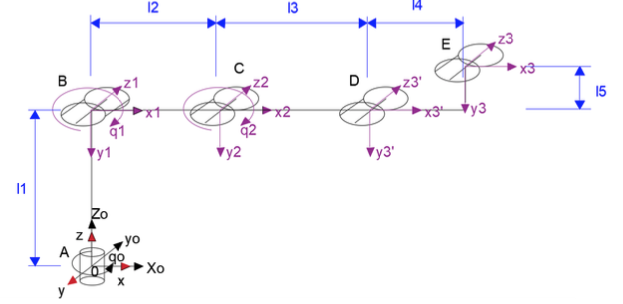
En base a la figura 4 se plantea la formulación matemática de la cinemática por medio de matrices homogéneas

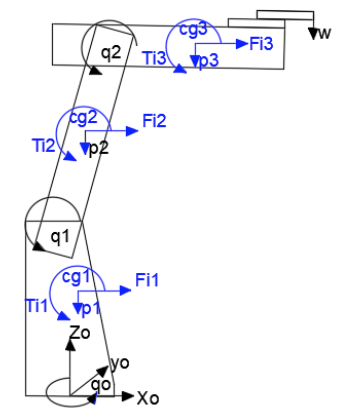
El análisis dinámico se desarrolló mediante el método de los trabajos virtuales juntamente con el principio de D’Alembert que es indispensable para el análisis dinámico puesto que considera los efectos generados por las inercias y aceleraciones (Roda, Mata, & Albelda, 2016); las ecuaciones se resolvieron utilizando Matlab. El método establece que para la resolución por coordenadas dependientes, las fuerzas debido a pesos (Pi), inercias (Fi, Ti) y fuerzas externas (W) deben ser multiplicadas por un factor de desplazamiento y es igual al Jacobiano total traspuesto multiplicado por los multiplicadores de Lagrange como se muestra en la ecuación 12.
Figura 5
Aplicación de cargas para aplicar el método de trabajos virtuales
-----
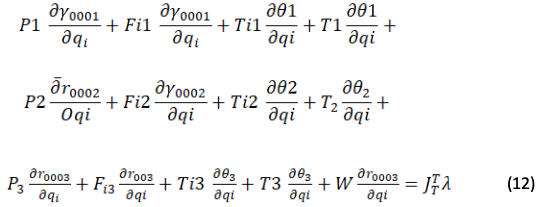
Luego de resolver la ecuación 12, se obtendrá una ecuación de escala que al ser derivada con respecto a las coordenadas lagrangianas generará tres ecuaciones con igual número de incógnitas. Con el objetivo de generar el análisis dinámico por el método de trabajos virtuales, es útil calcular las aceleraciones con respecto al centro de gravedad de cada elemento, como se muestra en la tabla 2, haciendo referencia a las ecuaciones 13, 14 y 15. Además, las velocidades y aceleraciones, pueden encontrarse mediante derivadas sucesivas de forma análoga a las ecuaciones 6 – 11.
Tabla 2
Centros de gravedad de los componentes del robot
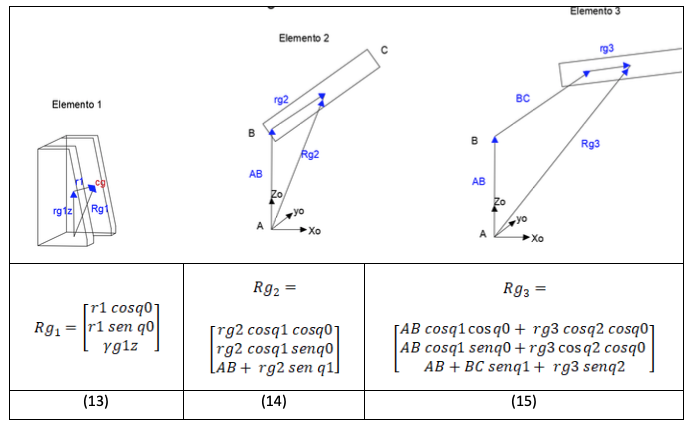
Figura 6
Trayectoria de la pinza
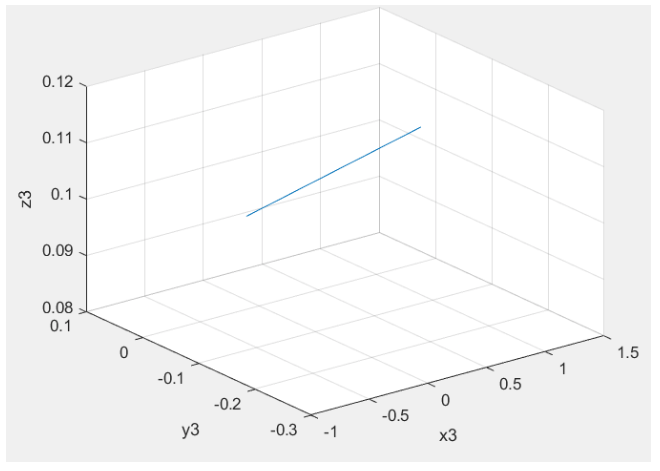
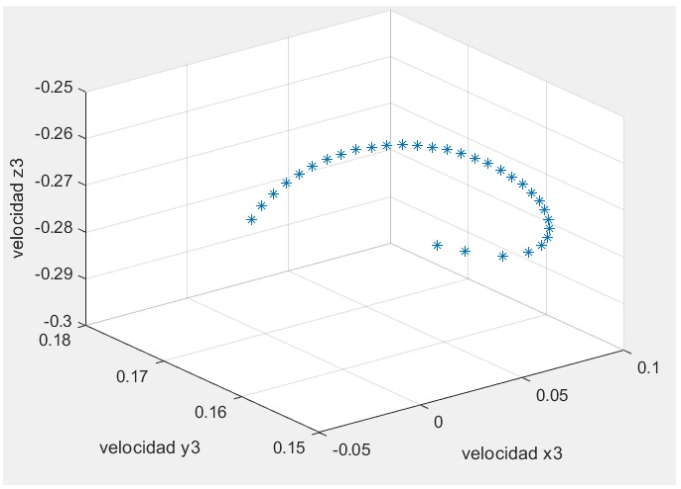
Dada la trayectoria rectilínea de la pinza, mostrada en la figura 6, se ha considerado que las velocidades angulares de los elementos del robot deben ser constantes, y tener un valor bajo (en este caso 0.5 rad/s). Por lo tanto, la aceleración angular de los elementos será cero, lo que conlleva a que no existan aceleraciones tangenciales; sin embargo, seguirán existiendo aceleraciones normales. Las gráficas de velocidad y aceleración se muestran en las figuras 7 y 8 respectivamente. Dado que los movimientos son suaves, las velocidades y aceleraciones decrecen a medida que el modelo sigue su trayectoria, lo que reduce la carga y el desgaste de los elementos.
Figura 7
Velocidad de la pinza
-----
Figura 8
Aceleración de la pinza

Las posiciones, velocidades y aceleraciones de los elementos en los rangos definidos en la metodología, fueron útiles para el cálculo de los torques en cada uno de los elementos del brazo robot. Utilizando programación en Matlab, se determinaron las curvas de torque con respecto al ángulo qi de donde se tiene que el torque en el elemento 1 tiende a cero, el elemento 2 es el más sobrecargado con un torque máximo de 20 Nm cuando el ángulo es de 5 como se muestra en la figura 9, mientras que el elemento 3 tiene un torque máximo de 12 Nm cuando el ángulo es 15.
Figura 9
Torque máximo versus ángulo de giro

El análisis se efectuó en ANSYS en el módulo static structural; se creó un material con parámetros físicos similares al cartón prensado, luego se importó la geometría en la posición donde el torque sería mayor (es decir cuando el elemento 2 del mecanismo llega a su posición horizontal), a continuación, se realizó un refinamiento de malla en los puntos críticos (uniones). Finalmente se aplicaron las cargas, mostradas en la figura 8.
Los resultados del análisis muestran un esfuerzo equivalente máximo localizado en los puntos de apoyo de 15.16 MPa y una deformación máxima localizada en la pinza de 0.046 mm. Por lo tanto, se muestra que los elementos del brazo robot resisten las cargas máximas que puedan ser aplicadas, tomando en cuenta que reciclará botellas PET de hasta 100 g.
Figura 10
Resultados de la simulación de esfuerzos en Ansys

Se preparó un brazo robot con el objetivo de que los estudiantes comprendan de una mejor manera la función de calidad; al seguir esta metodología los estudiantes pueden comprobar que las ecuaciones cinemáticas y dinámicas funcionan tomando en cuenta una trayectoria recta lo cual ayuda a impartir los principios físicos de los mecanismos. Además, la construcción de un prototipo del robot accionado por jeringuillas permite experimentar nuevas configuraciones y comprobar las ecuaciones matemáticas. Finalmente, el diseño del robot clasificador con 4 grados de libertad es adecuado dado que presenta buena resistencia, que la deformación máxima es aceptable y que mejora el proceso de dinámica de máquinas en los estudiantes de diseño mecánico.
EcuRed. (s.f.). Cinemática Inversa. Obtenido de https://www.ecured.cu/Cinem%C3%A1tica_Inversa
Grupo LYRSA. (2016). Un robot para clasificar los residuos. Obtenido de http://www.lyrsa.es/blog/174-un-robot-para-clasificar-los-residuos
HERNÁNDEZ MORETÓN, D. (25 de 06 de 2015). linkedin. Obtenido de Esfuerzo equivalente de Von Mises: https://www.linkedin.com/pulse/esfuerzo-equivalente-de-von-mises-david-hern%C3%A1ez-moret%C3%B3n
Krar, S., & Check, A. (2010). Tecnología de las máquinas herramientas. Alfaomega Grupo Editor.
López, S. A. (1997). QFD. El Despliegue de la función calidad en empresas de servicio. Madrid: Club Gestión de Calidad.
NBIO. (s.f.). Prácticas de Robótica utilizando Matlab. Obtenido de Dinámica de Robots: http://nbio.umh.es/files/2012/04/practica3.pdf
Noguera, J., García, O., & Robles, C. (1 de Septiembre de 2017). Modelado y control de un robot manipulador utilizando las técnicas de control estándar y H infinito. Revista Espacios, pág. 25.
RIBA, C. (2002). Diseño Concurrente. Barcelona.
Robles, C. A., Román, D. J., & Polo, A. M. (28 de Agosto de 2016). Brazo robótico con dieciocho grados de libertad tele-operado por un guante electrónico. Revista Espacios, pág. 22.
Roda, A., Mata, V., & Albelda, J. (2016). Máquinas y Mecanismos. Valencia: Universitat Politecnica de Valencia.
Roldán, J., Yime, E., & Sosa, J. (2018). Enhancing educational Robotics lab. ESPACIOS, 6.
Ruiz, S. M. (1994). QFD una herramienta del futuro. Bilbao: Labein.
S.B.M. (2014). Tecnología Electrónica. Recuperado el 2016, de http://tecnologiaelectron.blogspot.com/2014/02/circuito-de-mando-y-circuito-de-potencia.html
1. Profesor del Programa de Maestría en Diseño Mecánico. Escuela de Ingeniería Mecánica. Escuela Superior Politécnica de Chimborazo. Máster en Diseño Mecánico. saquino@espoch.edu.ec
2. Maestrante del Programa de Diseño Mecánico, Miembro del Grupo de investigación GIDAC-CEAA. Escuela Superior Politécnica de Chimborazo. Ingeniero Mecánico. Losmejores72@gmail.com
3. Maestrante del Programa de Diseño Mecánico, Miembro del Grupo de investigación GIDAC-CEAA. Ingeniero Mecánico. r_cordova@espoch.edu.ec
4. Directora del Grupo de Investigación GIDAC. Escuela Superior Politécnica de Chimborazo. Doctora en Química, Doctora en Ciencias Ambientales. m_echeverria@espoch.edu.ec