

 Vol. 40 (Nº 12) Año 2019. Pág. 11
Vol. 40 (Nº 12) Año 2019. Pág. 11
GARCÍA-GARCÍA, Jaime I. 1; ARREDONDO, Elizabeth H. 2; LÓPEZ-MOJICA, José M. 3 y ENCARNACIÓN-BALTAZAR, Eder J. 4
Recibido: 10/12/2018 • Aprobado: 25/03/2019 • Publicado 15/04/2019
RESUMEN: En el presente estudio se analizan los niveles de comprensión que exhiben estudiantes de Educación Secundaria (11-12 años), a través de sus respuestas a una tarea de leer e interpretar gráficas estadísticas, antes y después de haber realizado actividades de aprendizaje. Se utilizan los modelos jerárquicos de Curcio y de Aoyama para categorizar las respuestas. En general, los estudiantes muestran un avance en su nivel de comprensión, el cual probablemente fue producto por las actividades de aprendizaje que se llevaron a cabo. |
ABSTRACT: The present study analyzes the comprehension levels exhibited by Secondary Education students (11-12 years old), through their responses to a task of reading and interpreting statistical graphs, before and after having done learning activities. The hierarchical models of Curcio and Aoyama are used to categorize the answers. In general, students show an advance in their comprehension level, which was probably a product of the learning activities that took place. |
La sociedad actualmente interactúa con una gran cantidad de datos, mismos que son presentados mediante gráficas estadísticas para su divulgación. Por ejemplo, los medios de comunicación hacen uso de estas representaciones para divulgar algún tipo de información, ya sea política, social, deportiva, entre otras. Esto obliga a que los ciudadanos deban poseer una adecuada capacidad de comprensión gráfica para la toma de decisiones y entender su entorno (Díaz-Levicoy, Arteaga y Batanero, 2015). En este contexto, la enseñanza de la estadística ha ido tomando una creciente relevancia en los últimos años, ya que entrega las herramientas teóricas metodológicas necesarias para desarrollar dicha capacidad, la cual forma parte importante de una cultura estadística (Gal, 2002). Autores como Gal y Murray (2011) la consideran como la unión de dos componentes: (a) capacidad para interpretar y evaluar críticamente información estadística; y (b) capacidad de formular y comunicar opiniones respecto a dicha información. Al respecto, Sharma (2013) señala que un ciudadano estadísticamente culto debiera poder interpretar gráficas estadísticas elementales.
Por su parte, Estrella y Olfos (2012) manifiestan que el desarrollar un pensamiento más sofisticado dentro del proceso de representar datos, implica integrar tanto la comprensión gráfica (leer e interpretar gráficas) como el sentido gráfico (diseño de presentaciones gráficas de datos). Bajo esta perspectiva, consideramos la comprensión gráfica como la capacidad de leer e interpretar gráficas estadísticas, que le permite al individuo entender su entorno y por consiguiente la toma de decisiones.
En los últimos años, el desarrollo de la investigación sobre la comprensión gráfica se ha enfocado en tres aspectos: 1) identificar los niveles de lectura presentes en las actividades de los libros de texto (ver e.g., Díaz-Levicoy, Osorio, Arteaga y Rodríguez-Alveal, 2018; Díaz-Levicoy, Pino, Sepúlveda y Cruz, 2016; Díaz-Levicoy, Batanero, Arteaga y López-Martín, 2015; Díaz-Levicoy, Batanero, Arteaga y Gea, 2015; Díaz-Levicoy, Arteaga y Batanero, 2015; Díaz-Levicoy y Arteaga, 2014); 2) identificar el nivel de lectura que exhiben los estudiantes cuando responden preguntas referentes a la información representada (ver e.g., Batanero, Díaz-Levicoy, y Arteaga, 2018; Carmona y Cruz, 2016; Arteaga, Vigo y Batanero, 2017; Vigo, 2016; Ramírez-Leal, Hernández-Suárez y Prada-Núñez, 2016; Carranza, 2015; Evangelista, 2013; Fernandes y Morais, 2011; Tauber, 2010; Eudave, 2009; Monroy, 2007; Wu, 2004; Monteiro y Ainley, 2007); y 3) identificar el nivel de lectura que muestran los estudiantes cuando se les presenta sólo la gráfica sin ser guiados en su lectura (ver e.g., García-García, López y Arredondo, 2018; Gea, Arteaga y Cañadas, 2017; Arteaga, Batanero, Contreras y Cañadas, 2016; Inzunsa, 2015; Estrella y Olfos, 2012; Arteaga, 2011; Batanero, Arteaga, y Ruiz, 2010).
Este estudio está enmarcado bajo esta última línea de investigación, ya que en su cotidianidad el estudiante se enfrenta a representaciones gráficas sin una guía instruccional en el proceso. Si bien la comprensión no está condicionada con el planteamiento de preguntas dirigidas, el estudio contó con una intervención docente que tenía como propósito generar una estrategia de enseñanza para tal fin. Con base en lo anterior, se establecieron las siguientes preguntas que guiaron la investigación: ¿Qué niveles de comprensión presentan los estudiantes de primer grado de Educación Secundaria en México cuando realizan la interpretación de una gráfica circular y una de barras, antes y después de actividades de aprendizaje? ¿Qué rasgos característicos se presentan en las respuestas de los estudiantes?
Son varias las investigaciones dentro del área didáctica de la estadística que han explorado la comprensión gráfica por parte de estudiantes entre 10 y 15 años. Los intereses van desde la lectura, interpretación, inclusive traducción, tanto de gráficas (barras, de línea, de puntos, pictogramas) como de tablas estadísticas, por parte de estudiantes jóvenes entre 10 y 15 años o adultos.
Por ejemplo, Batanero, Díaz-Levicoy y Arteaga (2018) evalúan el nivel de lectura y la capacidad de traducción de pictogramas por 745 estudiantes de sexto y séptimo grado en Chile (11-12 años), encuentran que alrededor del 75% de los estudiantes traduce adecuadamente la información de un pictograma a una tabla; mientras que aproximadamente el 63% logra identificar si una afirmación realizada a partir de los datos del pictograma es correcta o no. Carmona y Cruz (2016) identifican las características que favorecen la comprensión de la información contenida en tablas y gráficas estadísticas en 55 estudiantes del grado séptimo (11-14 años) y observan que en su mayoría, las lecturas de los estudiantes se concentran en los niveles 1 y 2 (idiosincrático y lectura básica) de la jerarquía de Aoyama (2007).
Por su parte, Fernandes y Morais (2011) analizan el nivel de lectura alcanzado en la clasificación de Curcio (1989) por 108 alumnos del noveno curso en Portugal (13-14 años) y encuentran que prácticamente todos son competentes en leer los datos el primer nivel; sin embargo, sólo la tercera parte llega al nivel superior leer más allá de los datos. Evangelista (2013) analiza la lectura e interpretación de gráficas de barras y de líneas de 60 niños (10-11 años) de quinto grado de Educación Primaria en Brasil, a partir de 8 actividades enmarcadas en los niveles 1 y 2 de Curcio. Los resultados evidencian que el 59% de los estudiantes responde correctamente las actividades relacionas con las gráficas de barras, y el 43% con las gráficas de líneas.
Eudave (2009) realiza un estudio con 28 estudiantes de distintas edades que cursaban alguna de las modalidades de Educación Primaria o Secundaria para Adultos que se imparte en México y encontraron que únicamente cinco personas poseen los tres niveles de comprensión contemplados por Curcio, ya que realizan una lectura completa y adecuada de la tabla de frecuencias y de la gráfica de líneas. Por su parte, Monroy (2007) analiza el nivel de comprensión gráfica de 31 estudiantes (12-15 años) de Educación Secundaria en México, considerando el marco propuesto por Langrall y Mooney (2002). Los resultados muestran que la mayoría de los estudiantes está, sin distinción de grado, en el nivel idiosincrásico y/o transicional, presentando dificultades para distinguir los elementos de una gráfica y establecer relaciones dentro de esta. Wu (2004) analiza la interpretación gráfica de 907 estudiantes (13-15 años) de Educación Secundaria de Singapur, encontrando dificultades en tareas que requerían la realización de inferencias; por lo que exhiben niveles de lectura inferiores de Curcio.
Como se podrá notar, se identificó que no todos los estudiantes de Educación Primaria y Secundaria, de edades similares a los de nuestro estudio, alcanzan niveles superiores de comprensión gráfica; además, ninguno presenta la actividad de manera abierta, es decir, sin que se le guíe al estudiante en su proceso de lectura e interpretación. Lo anterior, según Eudave (2009), se debe a que entender una gráfica no es una tarea sencilla; pues los alumnos, por lo general, sólo alcanzan una comprensión superficial (descripción de los elementos más evidentes) sin establecer relaciones (entre los valores de una misma variable, ni entre los de dos o más variables).
Cabe destacar que en el primer grado de Educación Secundaria en México se aborda el tema Lectura de información representada en gráficas de barras y circulares, provenientes de diarios o revistas y de otras fuentes, correspondiente al eje Análisis y Representación de Datos, descrito en las directrices curriculares de la Secretaria de Educación Pública (SEP, 2011). Por este motivo el estudio se limita a gráficas del tipo circular y de barras.
La investigación se fundamenta en la constitución dos marcos de referencia: los niveles de lectura de Curcio (Curcio, 1989; Friel, Curcio y Bright, 2001) y la jerarquía de Aoyama (Aoyama, 2007). La interrelación de estos dos modelos jerárquicos permitirá analizar las respuestas de los estudiantes con el fin de establecer su comprensión gráfica (ver e.g., Batanero, Díaz-Levicoy y Arteaga, 2018; Gea, Arteaga y Cañadas, 2017; Carmona y Cruz, 2016). Inicialmente presentaremos las jerarquías que nos permitirán describir nuestro fenómeno de estudio y, posteriormente describiremos, a grandes rasgos, la interrelación que podemos establecer entre ellas.
Uno de los pioneros en proponer categorías para la comprensión gráfica fue Curcio (1989), quien postula tres niveles distintos:
Posteriormente, Friel, Curcio y Bright (2001) definen un cuarto nivel que requiere un conocimiento del contexto, ampliando la clasificación anterior:
Estos niveles de lectura han sido considerados como un modelo para evaluar y caracterizar la comprensión sobre gráficas estadísticas.
Otro de los modelos jerárquicos para categorizar la lectura de gráficas estadísticas es el desarrollado por Aoyama (2007), quien identifica cinco niveles diferentes de interpretación de gráficas:
El interés que surge, después de la presentación de estas jerarquías propuestas por Aoyama y Curcio, es identificar la relación que se puede establecer entre ellas. Lo primero que podemos destacar es la idea de que ambas establecen niveles jerárquicos, entonces, de manera natural podemos considerar, cuáles son las potencialidades de una respecto a la otra. La jerarquía establecida por Curcio y colaboradores, establece niveles de lectura apoyados en los referentes semióticos del gráfico que nos permiten relacionarlos, y perfila brevemente la posibilidad de valorar críticamente la información. Por otro lado, la jerarquía de Aoyama se enfoca más en una lectura apoyada en el nivel de valoración de la información, es decir, en un nivel crítico de esta. Por lo tanto, la interrelación de ambas categorías permite analizar la comprensión respecto a los elementos que componen una gráfica estadística del tipo circular y de barras, según la producción y/o respuesta de los estudiantes.
Dado que este trabajo se establece dentro del desarrollo de la cultura estadística (Gal, 2002) en estudiantes de secundaria, un fenómeno presente es la valoración crítica de los datos; por tanto se retoman los tres niveles superiores de Aoyama (racional/literal, crítico y elaboración de hipótesis y modelos) que pueden considerarse como subcategorías del nivel 4 (leer detrás de los datos) de Curcio.
El método empleado para esta investigación se realizó principalmente en el marco de un enfoque cualitativo (Vasilachis, 2006), ya que se analiza el nivel de comprensión presente en las respuestas de los estudiantes del primer grado de Educación Secundaria ante una tarea que involucra leer e interpretar gráficas estadísticas; antes y después de haber realizado actividades de aprendizaje.
Para seleccionar a los participantes se utilizó un muestreo no probabilístico por conveniencia, seleccionando 78 estudiantes entre 11 y 12 años de dos grupos de primer grado de Educación Secundaria de una escuela pública de la ciudad de Chilpancingo, Guerrero, México.
Para el diseño de una tarea relacionada con la comprensión de dos gráficas estadísticas, se realizó una revisión de los libros de texto de primer grado de Educación Secundaría entregados por la SEP en México; este fue uno de los criterios considerados para la propuesta de las gráficas, las que pueden notarse en algunos momentos con un abuso de elementos semióticos presentes, y esto estuvo en función a guardar una relación con el tipo de gráficas determinadas por la revisión. Cabe mencionar que los contextos en los que se colocaron las gráficas son comunes a los referentes culturales de los estudiantes.
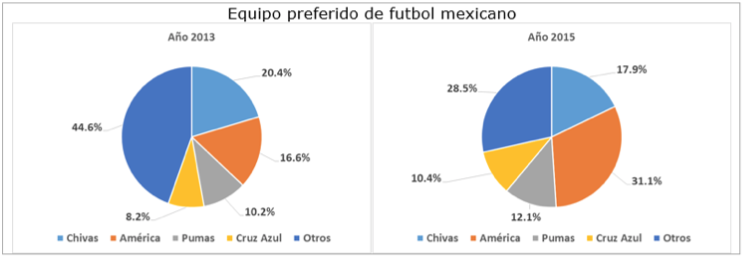
La primera gráfica, de tipo circular, expone el porcentaje correspondiente al equipo de futbol mexicano preferido en los años 2013 y 2015; mientras que la segunda, de barras, presenta el porcentaje de hogares con computadora y hogares con conexión a Internet durante los años 2013 a 2016. Cabe destacar que en el proceso de lectura e interpretación no se le guío al estudiante a través de preguntas, sino fue de manera abierta. En la Figura 1 y 2, se exponen las dos gráficas estadísticas de la tarea.
Figura 1
Gráfica 1 de la tarea de estudio
-----
Figura 2
Gráfica 2 de la tarea de estudio

Como podemos observar, la gráfica 1 no presenta fuente de información con la intención de identificar si los estudiantes consideran este elemento en su interpretación, ya que es esencial para la valoración crítica de los datos en cuanto a su validez y fiabilidad.
La investigación fue organizada en las siguientes cinco fases:
Fase 1. El profesor presenta a sus estudiantes la tarea de estudio (pre-test), les pide leer la instrucción en forma individual y grupal, y les permite hacer algunos comentarios para propiciar un mayor entendimiento sobre lo que deben realizar. El objetivo del pre-test es identificar el nivel de comprensión del estudiante antes de realizar las actividades de aprendizaje.
Fase 2. El estudiante desarrolla una actividad donde se requiere terminar la construcción de una tabla, una gráfica de barras y una gráfica circular, con la información dada; es decir, iniciada la construcción, que sirve de modelo al alumno, se pide completarla. Además, las hojas de trabajo contenían apartados con la información sobre la importancia de cada uno de los elementos de la gráfica (título, fuente, etc.). El profesor da seguimiento al desarrollo de la actividad.
Fase 3. El estudiante desarrolla una actividad que involucra la interpretación de diversas gráficas de barras y circulares, provenientes de diversos libros de texto, a partir de preguntas sobre la información presentada en cada uno de ellos. El profesor coordina las participaciones de los estudiantes.
Fase 4. El estudiante desarrolla una actividad que involucra la interpretación de diversas gráficas de barras y circulares, provenientes de revistas, periódicos y páginas de Internet. Las gráficas se presentan a través de un proyector con el propósito de que realicen su interpretación, de manera abierta, y contrasten sus observaciones con sus compañeros. El profesor coordina las participaciones y organiza las ideas de los estudiantes para dar sentido y coherencia a sus lecturas e interpretaciones.
Fase 5. El profesor aplica la tarea inicial (post-test), con el fin de identificar el nivel de comprensión de los estudiantes después de realizar las actividades de aprendizaje.
El análisis de los datos siguió un proceso cíclico y triangulación de expertos. Luego de una primera revisión, se realizó un análisis comparativo para observar rasgos característicos presentes en las respuestas de los estudiantes que hicieran referencia a una misma idea. Seguidamente, se crearon categorías cuyo concepto corresponde a la idea en común. Enseguida, se realizó una segunda revisión para establecer una jerarquía que contempla las categorías emergentes de los datos y los niveles descritos en el marco de referencia. Finalmente, se clasificó cada una de las interpretaciones de los estudiantes en los niveles establecidos. En la Tabla 1 se presenta la jerarquía obtenida para nuestro estudio, con la descripción de cada uno de los niveles y categorías.
Tabla 1
Jerarquía propuesta para la comprensión de gráficas estadísticas
Nivel de lectura |
Categoría |
Descripción |
Nivel 0. Lectura idiosincrática (N0) |
Reconocimiento (R) |
La lectura se basa en reconocer el tipo de gráfica que se le presenta; sin leer valores o elementos de la gráfica. |
Nivel 1. Leer los datos (N1) |
Variable (V) |
La lectura presenta palabras referentes a la(s) variable(s) de la gráfica, sin realizar interpretaciones ni cálculos adicionales. |
Título (T) |
La lectura presenta palabras referentes al título de la gráfica, sin realizar interpretaciones ni cálculos adicionales. |
|
Variable y frecuencia (V,F) |
La lectura presenta palabras referentes a la(s) variable(s) de la gráfica, así como sus frecuencias, sin realizar interpretaciones ni cálculos adicionales. |
|
Variable y título (V,T) |
La lectura presenta palabras referentes a la(s) variable(s) y al título de la gráfica, sin realizar interpretaciones ni cálculos adicionales. |
|
Variable, frecuencia y fuente (V,F,f) |
La lectura presenta palabras referentes a la(s) variable(s) y a la fuente de la gráfica, así como frecuencias de los valores de la(s) variable(s), sin realizar interpretaciones ni cálculos adicionales. |
|
Variable, frecuencia y título (V,F,T) |
La lectura presenta palabras referentes a la(s) variable(s) y al título de la gráfica, así como frecuencias de los valores de la(s) variable(s), sin realizar interpretaciones ni cálculos adicionales |
|
Nivel 2. Leer dentro de los datos (N2) |
Comparación horizontal (H) |
La lectura e interpretación presenta la comparación de datos que se incluyen en la gráfica de manera horizontal; es decir, identifica que existe un aumento/decremento en los valores de la(s) variable(s) y en algunos casos haciendo uso de operaciones aritméticas. |
Comparación vertical (V) |
La lectura e interpretación presenta la comparación de datos que se incluyen en la gráfica de manera vertical; es decir, identifica el valor de la variable con mayor frecuencia, o bien, ordenan los valores de la variable(s) de acuerdo a su frecuencia. |
|
Ambas comparaciones (A) |
La lectura e interpretación presenta ambos tipos de comparación. |
|
Nivel 3: Leer más allá de los datos (N3) |
Predicción de tendencia (PT) |
La lectura e interpretación presenta predicciones de tendencias sobre el comportamiento de los datos, considerando la información que se puede observar. |
Predicción de valores (PV) |
La lectura e interpretación presenta predicciones de valores del comportamiento de los datos, considerando la información que se puede observar. |
|
Nivel 4: Leer detrás de los datos (N4) |
Crítico (C) |
La lectura e interpretación presenta una valoración crítica del uso del gráfico, la recogida y organización de los datos, su validez o fiabilidad. |
Hipotético (H) |
La lectura e interpretación presenta conexión con el contexto; se acepta y evalúa la información formando hipótesis explicativas de lo observado. |
Fuente: Elaboración propia
En la Tabla 2 se presenta la trascripción de algunas respuestas de los estudiantes, clasificadas por nivel de lectura y categoría. Cabe señalar con las letras en negrita resaltan los aspectos que se consideraron para la clasificación de las respuestas. En concordancia con los elementos teóricos, los diálogos que se presentan en la segunda columna (de izquierda a derecha) corresponden a expresiones de los estudiantes a manera de tener lo más fiel posible su producción.
Tabla 2
Clasificación de acuerdo a nivel de lectura y categoría
Nivel de comprensión. Categoría |
Gráfica de la tarea/Transcripción de la respuesta de estudiante |
N0. Reconocimiento (R) |
Gráfica de barras Este se llama grafico de barras y del lado izquierdo se enumera cada línea puede ser de 1 en 1, o diferentes sucesiones, y del lado derecho se marca el porcentaje. |
N1. Variable (V) |
Gráfica circular Lo que se ve en el grafico es: cuantos le van a las chivas, al américa, a los pumas, etc. |
N1. Título (T) |
Gráfica de barras Es una gráfica que lleva los porcentajes de los hogares con computadoras y hogares con conexión a internet. |
N1. Variable y frecuencia (V,F) |
Gráfica circular En el año 2013 apoyaron el 20.4% de personas a chivas, y en el de américa fue el 16.6% de personas, y en el de pumas fueron un 10.2% de personas, pero en el de cruz azul fueron 8.2 y en otros equipos fueron 44.6%. En el año 2015 en chivas fueron 17.9% que apoyaron, en el de américa fueron 31.1% que apoyaron, y en pumas 12.1% fueron los que apoyaron, y en cruz azul fue un 10.4% que apoyaron, y los que apoyaron a otros equipos fue un 28.5 % que apoyaron. |
N1. Variable y título (V,T) |
Gráfica de barras En esta grafica se muestra el porcentaje de hogares con computadora y con conexión a internet. El porcentaje que se muestra en la parte izquierda es de 0 hasta el 100. En los gráficos azules se muestran los hogares con computadores y en el color anaranjado los hogares con conexión a internet. |
N1. Variable, frecuencia y fuente (V,F,f) |
Gráfica de barras En el 2013 se hizo una encuesta nacional (INEGI) sobre disponibilidad y uso de Tic en hogares y se hizo un porcentaje: el 35.8 tiene computadora en su hogar y el 30.7% tiene internet en su casa, en el 2014 el 38.3% tiene computadora en casa y el 34.4% tiene internet, en el 2015 el 44.9% tiene una computadora y el 39.2% tiene internet, en el 2016 el 45.6% tiene computadora y el 47% tiene conexión a internet. |
N1. Variable, frecuencia y título (V,F,T) |
Gráfica circular La gráfica es del equipo preferido del futbol mexicano y en el año 2013 los resultados los pusieron en una gráfica y los resultados fueron los siguientes 20.4% chivas, 8.2% cruz azul, 10.2% pumas, 16.6% américa, otros 44.6% y después en el año 2015 se hizo la misma encuesta y los resultados fueron estos 17.9% chivas, 10.4% cruz azul, 12.1% pumas, 31,1% américa y 28.5% otro. |
N2. Comparación horizontal (H) |
Gráfica de barras En 2013 a 2014 los hogares con computadora aumento 2.5% de 2014 a 2015 aumento 6.6% y de 2015 a 2016 aumento 0.7% |
N2. Comparación vertical (V) |
Gráfica circular Yo veo y entendí que el equipo preferido de futbol mexicano en el año 2013 fueron las chivas ya que obtuvo el mayor porcentaje de 20.4% y los demás equipos obtuvieron menos de 20.4%. En el año 2015 el equipo preferido fue américa obtuvo el 31.1% y los demás menos de 31.1%. |
N2. Ambas comparaciones (A) |
Gráfica de barras Yo entiendo que lo que pasan los años el número de hogares con computadora va aumentando al igual que el numero con conexión a internet, pero que en el 2016 los de internet rebasaron a los hogares con computadoras. |
N3. Predicción de tendencia (PT) |
Gráfica circular Que en el año 2013, otros tienen 44.6%, chivas 20.4%, América 16.6%, pumas 10.2% y en el otro año 2015 (otros 28.5%, cruz azul 10.4%, pumas 12.1%, américa 31.1%, chivas 17.9% y en el otro año 2016 va a crecer más el equipo américa y los demás irán disminuyendo. |
N3. Predicción de valores (PV) |
Gráfica de barras En 2013, 2014, 2015 los hogares con computadora eran superiores a los de conexión a internet, aumentaron en más o menos 3%, 6% y 1%, pero en 2016 eso cambio los hogares con conexión a internet fueron más que con computadora, tal vez en 2017 el número de hogares con conexión a internet aumente un 3% y sea más. |
N4. Crítico (C) |
Gráfica circular No tiene fuente de información, veo que dice otros, a que se refiere? porque no ponen de que otros equipos son también, observo que del año 2013 al 2015 disminuyo mucho el equipo de otros y también el de chivas y aumento mucho el del américa, aumento el de pumas y el que tiene mayor porcentaje es el del américa yo predigo que en el 2018 va a disminuir más el de otros equipos y va aumentar alguno de los demás equipos mencionados |
N4. Hipotético (H) |
Gráfica de barras Veo que en cada año las computadoras en casa van aumentando su porcentaje así como el internet en los hogares también se puede predecir que para los siguientes años puede subir su porcentaje así como disminuir porque cada familia necesita internet y computadoras, para su bienestar y beneficio. |
Fuente: Elaboración propia
En la Tabla 3 se muestran las frecuencias en las que se clasificaron las respuestas de los estudiantes de primer grado de Educación Secundaria por nivel de comprensión alcanzado, en el pre-test y post-test, y se presentan los índices de respuestas. Éstos se determinan asignando los valores 0, 1, 2, 3 y 4 respectivamente a cada nivel lectura y calculando la media ponderada de las frecuencias; en consecuencia, estos índices son números entre 0 y 4.
Tabla 3
Frecuencias de la clasificación de las respuestas de los estudiantes,
en el pre-test y post-test, por nivel de comprensión
Gráfica circular |
|||||||
Tarea |
Nivel de lectura |
Total |
Índice de respuesta (μ) |
||||
N0 |
N1 |
N2 |
N3 |
N4 |
|||
Pre-test |
4 |
20 |
51 |
0 |
3 |
78 |
1.72 |
Post-test |
0 |
8 |
33 |
17 |
20 |
78 |
2.63 |
Gráfica de barras |
|||||||
Tarea |
Nivel de lectura |
Total |
Índice de respuesta (μ) |
||||
N0 |
N1 |
N2 |
N3 |
N4 |
|||
Pre-test |
2 |
32 |
39 |
0 |
5 |
78 |
1.67 |
Post-test |
0 |
8 |
37 |
16 |
17 |
78 |
2.53 |
Fuente: Elaboración propia
El análisis de los resultados nos permitió observar que, en el pre-test, la mayoría de las respuestas se concentra en N2 y N1, leer dentro de los datos y leer los datos, al realizar una comparación con los datos o al efectuar la lectura literal de algún elemento de la gráfica. Pocas respuestas se categorizan en el N4, leer detrás de los datos, al presentar una conexión con el contexto de manera hipotética; mientras que otras sólo se limitan al reconocimiento o descripción de elementos visuales del tipo de gráfica, lectura idiosincrática (nivel 0). Cabe destacar que no presentaron respuestas en el N3, leer más allá de los datos. En el post-test, las respuestas se concentran en N2; sin embargo, existe un aumento en las frecuencias de los niveles superiores N3 y N4. Por otro lado, podemos observar en la Tabla 3 que el índice de respuesta, de ambas gráficas, aumento considerablemente en el post-test. Por tanto, conviene señalar que se puede atribuir una influencia en la comprensión de los estudiantes hacia niveles superiores después de las actividades de aprendizaje.
Con el objetivo de observar los avances o retrocesos en comprensión gráfica de los estudiantes de secundaria después de actividades de aprendizaje, en la Tabla 4 se consideran las frecuencias de la clasificación de manera conjunta.
Tabla 4
Frecuencias conjuntas de la clasificación de las respuestas de los estudiantes
Gráfica circular |
||||||
|
|
Post-test |
||||
|
|
N0 |
N1 |
N2 |
N3 |
N4 |
Pre-test |
N0 |
0 |
1 |
3 |
0 |
0 |
N1 |
0 |
6 |
6 |
5 |
3 |
|
N2 |
0 |
1 |
22 |
12 |
16 |
|
N3 |
0 |
0 |
0 |
0 |
0 |
|
N4 |
0 |
0 |
2 |
0 |
1 |
|
Gráfica de barras |
||||||
|
|
Post-test |
||||
|
|
N0 |
N1 |
N2 |
N3 |
N4 |
Pre-test |
N0 |
0 |
0 |
1 |
0 |
1 |
N1 |
0 |
6 |
15 |
8 |
3 |
|
N2 |
0 |
2 |
20 |
8 |
9 |
|
N3 |
0 |
0 |
0 |
0 |
0 |
|
N4 |
0 |
0 |
1 |
0 |
4 |
|
Fuente: Elaboración propia
El análisis conjunto de las respuestas de los estudiantes, en el pre-test y post-test, nos permite señalar que, de manera general, el 58% de ellos manifiestan un aumento en el nivel de comprensión alcanzado después de las actividades de aprendizaje, el 38% no muestran cambio, y sólo 4% presentan una disminución. Es natural esperar que después de realizar las actividades de aprendizaje exista un avance en la comprensión gráfica de los estudiantes de primer grado de Educación Secundaria; seguramente por haberse familiarizado con los elementos de las gráficas de barras y circular, y con los aspectos que pueden considerar en su lectura e interpretación.
Finalmente, la Tabla 5 exhibe las frecuencias de los rasgos característicos (categorías) que se presentan en las respuestas de los estudiantes de cada gráfica, en el pre-test y post-test.
Tabla 5
Frecuencias de los rasgos característicos (categoría)
presentes en las respuestas de los estudiantes
Nivel de lectura / Categoría |
Gráfica Circular |
Gráfica de barras |
||
Pre-test |
Post-test |
Pre-test |
Post-test |
|
N0. Reconocimiento (R) |
4 |
0 |
2 |
0 |
N1. Variable (V) |
6 |
6 |
7 |
0 |
N1. Título (T) |
0 |
0 |
1 |
2 |
N1. Variable y frecuencia (V,F) |
11 |
2 |
17 |
2 |
N1. Variable y título (V,T) |
2 |
0 |
4 |
2 |
N1. Variable, frecuencia y fuente (V,F,f) |
0 |
0 |
2 |
0 |
N1. Variable, frecuencia y título (V,F,T) |
1 |
0 |
1 |
1 |
N2. Comparación horizontal (H) |
16 |
11 |
17 |
13 |
N2. Comparación vertical (V) |
16 |
12 |
14 |
12 |
N2. Ambas comparaciones (A) |
19 |
10 |
8 |
12 |
N3. Predicción de tendencia (PT) |
0 |
15 |
0 |
12 |
N3. Predicción de valores (PV) |
0 |
2 |
0 |
4 |
N4. Crítico (C) |
0 |
14 |
0 |
11 |
N4. Hipotético (H) |
3 |
6 |
5 |
6 |
Fuente: Elaboración propia
La mayoría de las respuestas clasificadas en N1, que se caracterizan por la lectura literal de datos, dan cuenta que los estudiantes se enfocan en la variable y su frecuencia; en N2, que se caracterizan por la lectura de algo que no está explícitamente en la gráfica, se centran en la comparación de los datos, ya sea de manera vertical (al mencionar el valor de la variable con mayor frecuencia) u horizontal (al establecer un aumento o decremento); en N3, que implica la extensión de la información de la gráfica, se enfocan en predecir o establecer tendencias sobre aspectos que no están de manera explícita; y en N4, que se refiere a la valoración crítica de la información, se enfocan más en establecer conjeturas relacionadas con la fiabilidad de los datos.
Es indiscutible que en la sociedad actual el estudiante deba desarrollar una adecuada cultura estadística; es decir, un conocimiento básico de los conceptos estadísticos y probabilísticos. Una comprensión de razonamientos y argumentos estadísticos cuando se presenten dentro de un contexto más amplio, y una actitud crítica que se asume al cuestionar argumentos que estén basados en evidencia estadística (Watson, 2006); siendo este trabajo una contribución para el desarrollo de la comprensión gráfica de los estudiantes de primer grado de Educación Secundaria.
Las frecuencias de las respuestas a la tarea enfocada en la comprensión gráfica muestran una mejoría del pre-test al pos-test; aunque la mayoría de ellas se concentran en N2 en el pre-test, alrededor de 45% de los estudiantes logran alcanzar niveles superiores en el post-test; probablemente producido por las actividades que se llevaron a cabo. No es posible afirmar esto con certeza, pero el sólo hecho de proponer una tendencia o una crítica sobre la fiabilidad de los datos, ya es indicio de que se comienza a desarrollar una adecuada comprensión gráfica en el estudiante como parte de la cultura estadística que debe poseer.
Este trabajo permite visualizar los rasgos característicos presentes en las lecturas e interpretaciones de los estudiantes que hicieran referencia a una misma idea, observando que: 1) cuando realizan una lectura literal de la información representada en el gráfico, se enfocan en la(s) variable(s) su(s) frecuencia(s); 2) cuando efectúan una comparación de los datos, está la realizan de manera vertical, horizontal o ambas; 3) cuando proporcionan una tendencia sobre la información del gráfico, hacen alusión a un aumento o disminución en el comportamiento de los datos; y 4) cuando se cuestionan sobre la calidad de los datos, se enfocan en la existencia o no de la fuente de la información para dar fiabilidad a los datos.
Dentro de las debilidades que se identificaron en este estudio, destacamos el tipo de representaciones planteadas, ya que, por las características de estos, difícilmente le permiten a un estudiante generar reflexiones sobre tendencias entre los datos, en particular, la gráfica circular. Lo anterior nos deja entrever un viable objetivo a investigar en futuros trabajos al cuestionarnos ¿qué tan idóneas son las representaciones gráficas presentes en los libros de texto de Educación Secundaria en México para desarrollar una interpretación adecuada y crítica de la información?
Aoyama, K. (2007). Investigating a hierarchy of students’ interpretations of graphs. International Electronic Journal of Mathematics Education, 2(3), 298-318.
Arteaga, P. (2011). Evaluación de conocimientos sobre gráficos estadísticos y conocimientos didácticos de futuros profesores (Tesis de Doctorado). Universidad de Granada, España.
Arteaga, P., Batanero, C., Contreras, J. M. y Cañadas, G. (2016). Evaluación de errores en la construcción de gráficos estadísticos elementales por futuros profesores. RELIME, Revista Latinoamericana de Investigación en Matemática Educativa, 19(1), 15-40.
Arteaga, P., Vigo, J.M. y Batanero, C. (2017). Niveles de lectura de gráficos estadísticos en estudiantes de formación profesional. En J. M. Muñoz, A. Arnal, P. Beltrán, M.L. Callejo y J. Carrillo (Eds.), Investigación en Educación Matemática XXI (pp. 229-238). Zaragoza: SEIEM.
Batanero, C., Arteaga, P. y Ruiz, B. (2010). Análisis de la complejidad semiótica de los gráficos producidos por futuros profesores de educación primaria en una tarea de comparación de dos variables estadísticas. Enseñanza de las Ciencias, 28(1), 141-154.
Batanero, C., Díaz, C., Contreras, J. M. y Roa, R. (2013). El sentido estadístico y su desarrollo. Números. Revista de Didáctica de las Matemáticas, 83, 7-18.
Batanero, C., Díaz-Levicoy, D. y Arteaga, P. (2018). Evaluación del nivel de lectura y la traducción de pictogramas por estudiantes chilenos. Avances de Investigación en Educación Matemática, 14, 49-65.
Carmona, D. y Cruz, D. (2016). Niveles de comprensión de la información contenida en tablas y gráficas estadísticas: un estudio desde la jerarquía de Kazuhiro Aoyama (Tesis de Maestría). Universidad de Medellín, Colombia.
Carranza, F. (2015). Un estudio sobre la comprensión de gráficas estadísticas de profesores de secundaria (Tesis de Maestría). Universidad Autónoma de Guerrero, México.
Curcio, F. R. (1989). Developing graph comprehension. Reston, VA: NCTM.
Díaz-Levicoy, D. y Arteaga, P. (2014). Análisis de gráficos estadísticos en textos escolares de séptimo básico en chile. Revista Electrónica Diálogos Educativos, 14 (28), 21-40.
Díaz-Levicoy, D., Arteaga, P. y Batanero, C. (2015). Gráficos estadísticos y niveles de lectura propuestos en textos chilenos de Educación Primaria. En C. Fernández, M. Molina y N. Planas (Eds.), Investigación en Educación Matemática XIX (pp. 229-238). Alicante: SEIEM.
Díaz-Levicoy, D., Batanero, C., Arteaga, P. y Gea, M. (2015). Análisis de gráficos estadísticos en libros de texto de educación primaria española. UNION. Revista Iberoamericana de Educación Matemática, 44, 90-112.
Díaz-Levicoy, D., Batanero, C., Arteaga, P. y López-Martín, M. (2015). Análisis de los gráficos estadísticos presentados en libros de texto de educación primaria chilena. Educaçao Matematica Pesquisa, 17(4), 715-739.
Díaz-Levicoy, D., Osorio, M., Arteaga, P. y Rodríguez-Alveal, F. (2018). Gráficos Estadísticos en Libros de Texto de Matemática de Educación Primaria en Perú. BOLEMA. Boletim de Educação Matemática, 32(61), 503-525.
Díaz-Levicoy, D., Pino, C., Sepúlveda, A. y Cruz, A. (2016). Gráficos estadísticos en libros de texto chilenos de Ciencias Naturales. Didasc@lia: Didáctica y Educación, 7(4), 75-96.
Estrella, S. y Olfos, R. (2012). La taxonomía de comprensión gráfica de Curcio a través del gráfico de Minard: una clase en séptimo grado. Educación Matemática, 24(2), 123-133.
Eudave, D. (2009). Niveles de comprensión de información y gráficas estadísticas en estudiantes de centros de educación básica para jóvenes y adultos de México. Educación Matemática, 21(2), 5-37.
Evangelista, B. (2013). Aprendendo a representar escalas em gráficos: um estudo de intervenção (Tesis de Maestría). Universidade Federal de Pernambuco, Brasil.
Fernandes, J. A. y Morais, P. C. (2011). Leitura e interpretação de gráficos estatísticos por alunos do 9º ano de escolaridade. Educação Matemática Pesquisa, 13(1), 95-115.
Friel, S., Curcio, F. y Bright, G. (2001). Making sense of graphs: critical factors influencing comprehension and instructional implications. Journal for Research in mathematics Education, 32(2), 124-158.
Gal, I. (2002). Adult´s statistical literacy: Meaning, components, responsibilities. International Statistical Review, 70(1), 1-25.
Gal, I. y Murray, S. T. (2011). Responding to diversity in users' statistical literacy and information needs: Institutional and educational implications. Statistical Journal of the International Association for Official Statistics, 27(3-4), 185-195.
García-García, J. I., López, C y Arredondo, E. H. (2018). Interpretación de una tabla y una gráfica circular por estudiantes de licenciatura. TANGRAM. Revista de Educação Matemática, 1(3), 24-39.
Gea, M., Arteaga, P. y Cañadas, G. (2017). Interpretación de gráficos estadísticos por futuros profesores de Educación Secundaria. Avances de Investigación en Educación Matemática, 12, 19-37.
Inzunsa, S. (2015). Niveles de interpretación que muestran estudiantes sobre gráficas para comunicar información de contextos económicos y sociodemográficos. Revista mexicana de investigación educativa, 20(65), 529-555.
Langrall, C. W. y Mooney, E. S. (2002). The development of a framework characterizing middle school student´s statistical thinking. En B. Phillips (Ed.), Proceedings of the Sixth International Conference on Teaching Statistics (pp. 1-6). Voorburg, the Netherlands: ISI.
Monroy, R. (2007). Categorización de la comprensión de gráficas estadísticas en estudiantes de secundaria (12-15). Revista Electrónica de Investigación en Educación en Ciencias, 2(2), 29-38.
Monteiro, C. y Ainley, J. (2007). Investigating the interpretation of media graphs among student teachers. International Electronic Journal of Mathematics Education, 2(3), 188-207.
Ramírez-Leal, P., Hernández-Suárez, C. y Núñez, R. (2016). Nivel de razonamiento en la comprensión de gráficos estadísticos en estudiantes universitarios. Respuestas, 21(2), 13-23.
SEP (2011). Programas de estudio: Guía para el maestro, Educación Básica Secundaria. México: Secretaría de Educación Pública.
Sharma, S. (2013). Assessıng students’ understandıng of tables and graphs: implıcatıons for teachıng and research. International Journal of Educational Research and Technology, 51-70.
Tauber, L. (2010). Análisis de elementos básicos de alfabetización estadística en tareas de interpretación de gráficos y tablas descriptivas. Ciencias Económicas. Revista de la Facultad de Ciencias Económicas de la UNL, 8(1), 53-67.
Vasilachis, I. (2006). Estrategias de investigación cualitativa. Barcelona, España: Gedisa.
Vigo, J. (2016). Comprensión de gráficos estadísticos por alumnos de formación profesional (Tesis de maestría). Universidad de Granada, España.
Watson, J. M. (2006). Statistical literacy at school: Growth and goals. Mahwah, NJ: Lawrence Erlbaum Associates.
Wu, Y. (2004, Julio). Singapore secondary school students’ understanding of statistical graphs. Trabajo presentado en el 10th International Congress on Mathematics Education (ICME-10). Copenhagen, Dinamarca.
1. Doctor en Ciencias, Especialidad en Matemática Educativa. Departamento de Ciencias Exactas. Universidad de Los Lagos. Correo electrónico: jaime.garcia@ulagos.cl
2. Doctora en Ciencias, Especialidad en Matemática Educativa. Departamento de Ciencias Exactas. Universidad de Los Lagos. Correo electrónico: elizabeth.hernández@ulagos.cl
3. Doctor en Ciencias, Especialidad en Matemática Educativa. Facultad de Matemáticas. Universidad Autónoma de Guerrero. Correo electrónico: mojicajm@uagro.mx
4. Maestro en Docencia de la Matemática. Universidad Autónoma de Guerrero. Correo electrónico: earencarnacionbaltaz@gmail.com