ISSN 0798 1015

Vol. 40 (Nº 9) Año 2019. Pág. 30

Análisis de la eficiencia global de las 50 mejores universidades del mundo

Ranking of global efficiency of the 50 best universities in the world

BLANCO CANTO, Miguel 1; BARES LÓPEZ, Lydia 2; HRYNEVYCH, Oksana 3

Recibido: 29/11/2018 • Aprobado: 26/02/2019 • Publicado 25/03/2019

Contenido

1. Introducción

2. Metodología

3. Resultados

4. Conclusiones

Referencias bibliográficas

1. Introducción

Las universidades del siglo XXI desarrollan una importante actividad académica que permite el desarrollo cultural, económico y social de los países industrializados. Este rol está haciendo que se conviertan en elementos estratégicos nacionales, sobre todo para un contexto internacional como el actual, caracterizado por procesos de globalización y tercerización de las economías territoriales que están poniendo en juego el orden económico internacional establecido desde hacía décadas.

Sin embargo, desde el año 2008, la reciente crisis económica ha provocado a nivel global una disminución de los gastos e inversiones de políticas públicas en formación. El siguiente gráfico construido a partir de los datos suministrados por el Banco Mundial así lo confirma.

Gráfico 1
Gasto mundial por alumno por niveles educativos.

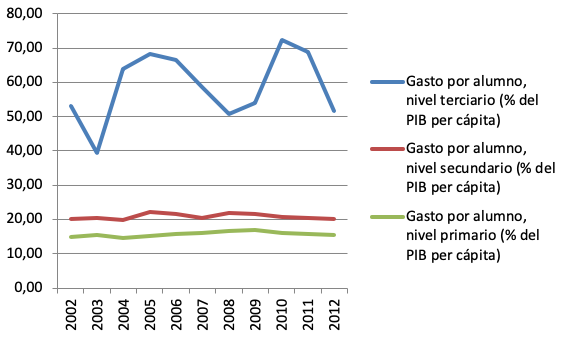
Fuente. Banco mundial [4]      

A nivel de países de la Organización para la Cooperación y el Desarrollo Económicos (OCDE), la situación es distinta. Desde el año 2002, se ha ido incrementando la inversión en gasto por alumno. Lo que pone de manifiesto los datos aportados, es que a partir de 2005, el gasto en educación primaria, secundaria y postsecundaria no terciaria supera al de la educación terciaria.

Gráfico 2
Variación del gasto por alumno y del número de estudiantes, por nivel educativo.
Índice de variación entre 2000 y 2012 (deflactor del PIB 2005=100, precios constantes)

Fuente. Indicadores de la OCDE. 2000-2016

A pesar de la información suministrada en los gráficos 1 y 2, las sociedades demandan al mundo universitario, además de la tradicional función docente, un aumento de la investigación de excelencia, un apoyo decidido a la mejora de la gestión e innovación empresarial y un incremento del grado de empleabilidad de sus ciudadanos. Así, la investigación científica ha constituido la piedra angular sobre la que se han construido las universidades, cuyos resultados, para que contribuyan al desarrollo social, deben ser transferidos en general a la sociedad, y en particular, al mundo empresarial. Sin embargo, y sobre todo desde el año 2008, como consecuencia del incremento experimentado en los niveles de desempleo entre los países de la OCDE, aumenta la importancia de las universidades como entidades necesarias para dotar al mercado laboral de trabajadores altamente cualificados y demandados por las empresas.

En el siguiente gráfico 3 se muestra la evolución de las tasas de desempleo por nivel de formación. En él se muestra el mayor nivel de inserción profesional de sus egresados en relación con otros niveles educativos.

Gráfico 3
Evolución de las tasas de desempleo por el nivel de formación (2004-2016)

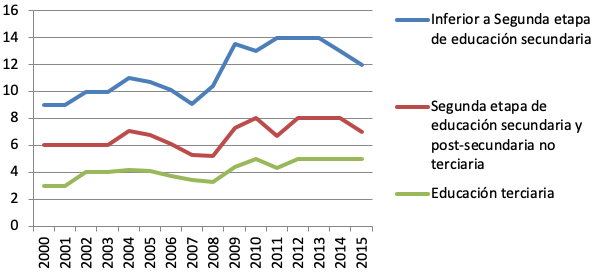
Fuente. Indicadores de la OCDE. 2004-2016

Estos datos obligan a justificar, en términos de cumplimiento de objetivos, las inversiones realizadas en educación. Esto implica la necesidad de incluir el concepto de eficiencia en cada uno de los fines que deben cumplir las universidades, tanto en materia de docencia e investigación como de empleo de sus egresados. Para ello, deberá elegir el output que maximice el beneficio, la combinación óptima de inputs que minimice los costes de producción o producir el producto utilizando para ello la menor cantidad posible de inputs (Álvarez, 2001).

Este concepto de eficiencia es una ratio netamente empresarial. Sin embargo, en las últimas décadas se ha ido trasladando al campo de las políticas públicas, de tal manera que, además de las tradicionales evaluaciones administrativas de tipo legal, económico y administrativo, se ha ido imponiendo la necesidad de realizar evaluaciones de cumplimiento de objetivos, eficiencia y eficacia. Esto obliga a elegir una serie de inputs y outputs ligados a la actividad pública y analizar los procesos de conversión que existen entre ellos. Para este trabajo de investigación se aplica un concepto de eficiencia global en la gestión universitaria. En su concepción se han elegido una serie de outputs que recogen de manera sintética las tres funciones básicas de la actividad universitaria. En concreto,

- una mejora en la capacitación profesional de sus estudiantes para que puedan competir en el acceso a un puesto de trabajo en un entorno cada vez más globalizado

- la capacidad de generar y transmitir los conocimientos científicos y tecnológicos.

- la modernización del sistema económico nacional mejora de la actividad empresarial.

Por ello, el objetivo general de este artículo es la determinación de un ranking de eficiencia global de las cincuenta mejores universidades del mundo. Esto implica un análisis de su actividad investigadora, de su apoyo al tejido empresarial y de su función en la mejora del grado de inserción laboral de sus egresados universitarios.

La estructura de este artículo es la siguiente: tras la introducción, en la cual se justifica esta investigación, en el siguiente epígrafe se analiza el concepto de eficiencia desde la perspectiva universitaria. En el tercer apartado se presenta y justifica la aplicación metodológica propuesta. En el cuarto se recogen los resultados obtenidos y finalmente se presentan las conclusiones y una propuesta de debate.

1.1. Eficiencia universitaria

Con carácter previo a la determinación metodológica de este artículo se ha realizado un extenso trabajo de recopilación del material bibliográfico en el cual los autores han realizado análisis comparativos interuniversitarios. Así se ha podido constatar que es relativamente frecuente la publicación de rankings universitarios en los cuales se definen una serie de variables cuantificables que permiten determinar la posición relativa de cada una de las universidades en comparación con el resto. A nivel global destacan los realizados por la Academic Ranking of World Universities (Shanghai Ranking Consultancy), el World University Rankings (Times Higher Education), Performance Ranking of Scientific Papers for World Universities (Higher Education Evaluation and Accreditation Council of Taiwan), Ranking Web of World Universities (Cybermetrics Lab (CCHS), una unidad del Consejo Superior de Investigaciones Científicas (CSIC)), UTD Top 100 Business School Research Rankings (UT Dallas' School of Management) y QS World University Rankings (Quacquarelli Symonds).

Para áreas territoriales concretas, destacar el Ranking de Escuelas Superiores elaborado por el Centro para el Desarrollo Universitario (CHE) y el periódico DIE ZEIT, el Ranking de la Fundación Humboldt, el USNews 2014 College Rankings (America's Best Colleges 2014), el Top American Research Universities, el Financial Times Business Education Rankings, el Marr/Kirkwood Side by Side Comparison by Side Comparison of Business School Rankings, los Princeton Review Rankings, Rankings de Facultades de Derecho de la Internet Legal Research Group, el ranking elaborado por la Universidad de Jiao Tong (China), el ranking publicado por el Laboratorio de Internet del CINDOC (CSIC), la publicación Asiaweek perteneciente al Grupo Time en Asia, la Australian Education Network o el Netbig que publica anualmente un ranking de universidades chinas.

Con carácter general, en estos rankings, sus autores definen una serie de variables de producción, como suelen ser el número de publicaciones, el número de alumnos que finalizan sus estudios universitarios, o el número de premios nobel que cuentan entre sus profesores o egresados. A continuación, ponderan dichas variables en relación con la importancia relativa que le dan a cada una de ellas. Finalmente calculan un indicador global adicionándolas.

Sin embargo, existen pocos estudios que tengan en consideración variables de entrada –inputs- y variables de salida –outputs-. Fundamentalmente por las dificultades asociadas a las características propias de este tipo de organizaciones, como pueden ser la ausencia de ánimo de lucro así como el hecho de producir varias salidas de múltiples entradas (Peñate, Rivero y Lozada, 2017). Y los que existen tienen un contenido territorial muy concreto. Así, Abbott y Doucouliagos (2003) lo aplican a las universidades australianas, Johnes y Li (2008) en China, Pino et al. (2010) en Andalucía, Kuah y Wong (2011) en Asia, Wolszczak-Derlacz (2017) en Europa y Estados Unidos, y Sagarra, Mar-Molinero y Agasisti, (2017) en México.

En estos últimos, la metodología empleada es un análisis DEA. Sin embargo, la mayoría de ellos se centran en la realización de un análisis comparativo de eficiencia utilizando para ello variables inputs/outputs relacionadas fundamentalmente con la actividad científica. Obvian de esta manera el aspecto de compromiso que tienen las universidades en la cooperación con el desarrollo empresarial, así como la función de mejora del grado de inserción laboral de sus alumnos.

Por ello, en este artículo se propone aplicar la metodología DEA sobre un concepto de eficiencia global que recoja las tres grandes funciones que tienen las universidades, lo cual constituye una novedad importante sobre la literatura revisada. Además, mientras que en los trabajos académicos publicados el ámbito territorial son países o regiones concretas, en este trabajo se ha aplicado sobre las cincuenta mejores universidades del mundo.

En toda organización económica o social debe definirse una relación entre sus inputs y sus outputs que permita una gestión de máxima eficiencia en la utilización de sus recursos materiales tangibles e intangibles y humanos. Para ello, los gestores suelen utilizar diversos análisis de eficiencia, entre los cuales se encuentran los denominados “modelos de frontera”. En ellos se define una función de producción en la cual se relacionan variables de entrada y de salida y se aplica a distintas unidades operativas o Decision Making Units (DMU´s). Los resultados permiten determinar la posición relativa que ocupa cada una de ellas con respecto a una frontera de eficiencia ideal –reliability yardstick-. La máxima eficiencia supone que una determinada DMU ha utilizado sus entradas y salidas de recursos de tal manera que los resultados obtenidos se encuentran sobre la curva de frontera óptima. Cuanto más se alejan los resultados de ese punto, menor será la eficiencia de las organizaciones.

La función de producción puede ser definida por técnicas de carácter paramétrico o no paramétrico. En este artículo se ha utilizado la metodología no paramétrica DEA propuesta por Charnes, Cooper y Rhodes (1978) por ser una herramienta de investigación que, a pesar de los años transcurridos desde que originariamente fue propuesta por sus autores, actualmente sigue utilizándose con frecuencia en las investigaciones. Con carácter general, aplicada a los análisis de eficiencia de las organizaciones empresariales, y de manera específica en los estudios asociados al sector de la educación (Johnes y Li, 2008; Emrouznejad y Yang, 2017).

Con carácter previo a su aplicación, se ha realizado un análisis exhaustivo de los principales inputs y outputs utilizados por los autores en la elaboración de sus estudios de eficiencia aplicados al sector universitario. Se ha podido constatar cómo, de manera recurrente, los autores utilizan variables como el número de estudiantes de primer y segundo ciclo, número de estudiantes de tercer ciclo, número de profesores funcionario y contratado, gastos de personal, gastos de personal de administración y servicios, número de publicaciones, ayudas externas a la investigación, número de tesis y número de citas aplicadas a diferentes ámbitos territoriales. Entre las principales investigaciones analizadas, destacar las realizadas por Abbott y Doucouliagos (2003), Johnes y Li (2008), Pino et al. (2010), Kuah y Wong (2011), Wolszczak-Derlacz (2017), Sagarra, Mar-Molinero y Agasisti, (2017), Fernández y Minaya (2017), así como Blanco, Bares y Hrynevych (2018).

En concreto, Abbott y Doucouliagos (2003) aplican el análisis envolvente de datos a las universidades australianas. Las variables inputs utilizadas fueron el número total de personal académico (equivalente a tiempo completo), el número de personal no académico (equivalente a tiempo completo) y los gastos corrientes del resto de insumos relacionados con las contrataciones. En cuanto a las variables outputs utilizadas se encuentran las relacionadas con la producción docente, el número de estudiantes a tiempo completo, el número de títulos de grado y de posgrado y los alumnos matriculados en ellos.

Johnes y Li (2008) enfocan territorialmente su estudio a China. Entre los inputs utilizados se encuentran la proporción de estudiantes a tiempo completo del personal, la proporción de profesores asociados, los estudiantes de doctorado, los gastos de investigación, los libros y los edificios. Como variables outputs se encuentran el índice total de publicaciones de investigación y el número de publicaciones de investigación por miembros del personal académico.

Pino et al. (2010) aplican el DEA a los grupos de investigación de la comunidad autónoma de Andalucía. Como inputs utilizan recursos humanos (Número de doctores activos, número de titulados superiores, número de titulados medios, personal auxiliar y becarios), y recursos financieros (subvenciones recibidas en la convocatoria de ayudas a los grupos de investigación). Como outputs incorporan datos provenientes de publicaciones, aportaciones a congresos, tesis, propiedad industrial, proyectos, contratos y comités de revistas.

Kuah y Wong (2011) analizan la eficiencia entre universidades asiáticas. Como insumos utilizados se encuentran los relacionados con el personal académico, los estudiantes, los títulos universitarios expedidos y las becas de investigación. Entre los outputs se encuentran el número de graduados, la tasa de empleo de los graduados, el número de graduados en investigación, las publicaciones, los premios obtenidos y el número de patentes.

Wolszczak-Derlacz (2017) toma como ámbito geográfico de su publicación las universidades europeas y de Estados Unidos. Desarrolla cuatro modelos. En el modelo 1, las variables utilizadas son las relacionadas con el personal académico, los ingresos totales y la cantidad de estudiantes. Como outputs se encuentran el número de publicaciones y graduados. Para el modelo 2 los inputs serían el personal académico y los ingresos totales. Los outputs estarían constituidos por el número de publicaciones y graduados. El modelo 3 utiliza las siguientes variables. Como inputs el personal académico, no académico, los ingresos totales y el número de estudiantes. Como outputs el número de artículos científicos. Finalmente el modelo 4 relaciona los ingresos totales con las publicaciones y el número de graduados.

Fernández y Minaya (2017) analizan la eficiencia de las Universidades Públicas Autónomas del Estado Plurinacional de Bolivia durante los años 2014 y 2015. Las variables inputs utilizadas fueron el número total de docentes y el número total de trabajadores administrativos. En cuanto a las variables outputs utilizadas fueron el número total de matriculados, el número total de titulados y el número total de matrícula nueva.

Sagarra, Mar-Molinero y Agasisti, (2017) analizan el nivel de eficiencia entre universidades mexicanas. Como inputs utilizan variables relacionadas con el personal docente a tiempo completo, el número de alumnos matriculados y el número de alumnos que finalizan sus estudios. Como outputs se encontrarían el número de publicaciones en Scopus y el número de graduados.

Finalmente, Blanco, Bares y Hrynevych (2018) establecen un ranking de universidades europeas según su grado de eficiencia global. Entre las variables inputs utilizadas se encuentran las relacionadas con el número de alumnos de grado y de posgrado tanto nacionales como extranjeros así como el número de profesores. Como outputs utilizan variables relacionadas con el empleo de sus egresados universitarios, patentes y publicaciones.

Como se puede apreciar, las investigaciones analizadas toman como referencia geográfica unidades territoriales concretas. En este artículo se han tenido en cuenta las 50 mejores universidades del mundo. Asimismo, en los análisis consultados se aprecia como las variables utilizadas por los autores recogen aspectos concretos de la actividad universitaria. En nuestra investigación, se trabaja con un concepto de eficiencia global que incluye: 

- la formación de profesionales con un elevado nivel cultural, científico y técnico que puedan ser insertados profesionalmente en los procesos productivos de las organizaciones tanto de carácter empresarial como social.

- la generación y transmisión de los conocimientos científicos y tecnológicos.

-la modernización del sistema económico nacional mejora de la actividad empresarial.

En la tabla 1 se recogen las variables inputs/outputs utilizadas en la función de producción de esta investigación asociada a los tres fines básicos de la educación superior.

Tabla 1
Variables input/output utilizadas en la función de producción de eficiencia global universitaria.

Las fuentes utilizadas para obtener los datos han sido las siguientes:

            - QS Graduate Employability Rankings [5]

            - Ranking Académico de las Universidades del Mundo (ARWU) [6]

            - World's Most Innovative Universities [7]

Una de las principales dificultades que señalan los autores analizados en la determinación de las variables de entrada y salida asociadas a la función de producción radica en el hecho de que resulta difícil determinar de manera directa la conversión de inputs en outputs. Así, al no existir certeza sobre el tipo de retorno de la función, se ha asumido un modelo tipo BCC-Output el cual arroja una medida de la eficiencia técnica pura, ignorando de esta manera el tamaño de la escala ya que compara sólo una DMU a una unidad de escala similar (Martić, Novaković, y Baggia, 2009). De esta manera, lo que se propone es la maximización de la siguiente expresión:

Una vez definida la función, la frontera de eficiencia quedaría integrada por todas aquellas DMU en las cuales concurre la circunstancia de máxima eficiencia global. Una vez determinada dicha reliability yardstick, el DEA compara cada una de las universidades objeto de análisis, bajo el supuesto de que las desviaciones detectadas indican un cierto grado de comportamiento ineficiente. De esta manera se puede medir la eficiencia relativa de un conjunto de universidades que producen un tipo de output a partir de un conjunto de inputs.

Se han realizado cuatro tipos de análisis DEA:

DEA 1: Análisis de eficiencia en la gestión de patentes. En él se ha relacionado, como output, el número de patentes de cada universidad utilizando para ello los datos ofrecidos por el indicador World's Most Innovative Universities. Para los inputs se han utilizado el número de estudiantes que están cursando estudios de grado y de posgrado, así como el número de profesores, tanto nacionales como extranjeros.

DEA 2: Análisis de eficiencia en publicaciones. En este caso, se han mantenido los inputs y solamente se ha utilizado como outputs el número de investigaciones realizadas y contabilizadas mediante el indicador que proporciona el Ranking Académico de las Universidades del Mundo –ARWU).

DEA 3: Análisis de la eficiencia de la inserción laboral de los egresados universitarios. En este caso el output utilizado es el proporcionado por el QS Graduate Employability Rankings.

DEA 4: Análisis de le eficiencia global. En su cálculo se han utilizado tres variables output relacionadas con la actividad innovadora (World's Most Innovative Universities), la actividad investigadora (Ranking Académico de las Universidades del Mundo –ARWU-) y la actividad relacionada con la mejora del grado de ocupabilidad de sus egresados universitarios (QS Graduate Employability Rankings).

Asimismo, con los resultados obtenidos se han realizado análisis de correlación para determinar la relación de dependencia que existen entre cada uno de los resultados obtenidos mediante la aplicación del DEA.

Para mejorar la confiabilidad de la función de producción que se propone se ha considerado necesario cumplir con la Regla de Cooper (Charnes y Cooper, Wei y Huang 1990), según la cual ha de existir una relación concreta entre DMU’s e inputs y outputs. En especial, la regla indica que:

DMU’s ≥ α (input + outputs)

Así, el número de DMU’s a considerar en el modelo debe ser mayor o, al menos, igual a α veces la suma de los inputs y los outputs. La regla establece que el valor mínimo a asumir es α = 3 aunque muchos autores, con la finalidad de garantizar resultados más robustos, suelen asumir valores superiores a 3 (Belmonte y Plaza, 2008; Pastor, 1995; Bartual y Garrido, 2011). En  todos los cálculos DEA efectuados se cumple dicha regla.

Las universidades que se han seleccionado para el análisis DEA son aquellas que ocupan los 50 primeros puestos en los tres listados de ranking consultados. El listado se detalla en la tabla 2.

Tabla 2
DMU´s utilizadas en el análisis DEA Global

Para la estimación de la eficiencia global se asumen rendimientos variables a escala y una orientación hacia la maximización de los outputs seleccionados –patentes, empleo de sus egresados y publicaciones- según un modelo BBC-output, sin conocimiento previo de los rendimientos a escala que puedan generarse frente a la cantidad de inputs aplicados en la función de producción maximizadora.

La siguiente tabla recoge un resumen de los estadísticos correspondientes a las variables de entrada y salida que se han definido en la función de producción.

Tabla 3
Resumen estadísticos básicos variables inputs/outputs para la función de producción

3.1. DEA 1: Análisis de eficiencia en la gestión de patentes

En este análisis se han utilizado las variables inputs relacionadas con el alumnado y el profesorado y una sola variable output que mide el número de patentes según los datos del World's Most Innovative Universities. Las universidades elegidas en este DEA han sido las primeras 50 de las que se tenía información en las tres bases de datos utilizadas.

Los datos aparecen en la tabla 4 recogen, en la primera columna, la puntuación obtenida. En la segunda columna aparece el esfuerzo que debería de realizar la Universidad para situarse en el nivel óptimo de eficiencia.

Tabla 4
Resultados y objetivos DEA1

3.2. DEA 2: Análisis de eficiencia en publicaciones

En este análisis se han utilizado las mismas variables inputs que para el DEA 1. Sin embargo, el output elegido en esta ocasión es el valor obtenido a partir de la información suministrada por el Ranking Académico de las Universidades del Mundo –ARWU-.

Tabla 5
Resultados y objetivos DEA2.

3.3. DEA 3: Análisis de la eficiencia de la inserción laboral de los egresados universitarios

Para el análisis DEA3, la principal variación con respecto a los anteriores análisis envolvente de datos ha sido la elección del output. En este caso la información utilizada ha sido suministrada por el QS Graduate Employability Rankings).

Tabla 6
Resultados y objetivos DEA3.

3.4. DEA 4: Análisis de le eficiencia global

En la tabla 7 se muestran los resultados obtenidos de la aplicación del modelo DEA eficiencia global. En ella se recoge en la columna score la posición relativa de cada universidad con respecto a un punto óptimo al que se le ha signado un valor 100. Dicha columna es la que ha servido como criterio para establecer el orden entre las DMU´s. Asimismo aparecen las columnas target Q1 empleo, target Q2 publicaciones y target Q3 patentes. En ellas se especifica el porcentaje de incremento que deberían realizar las universidades para llegar a una situación de máxima eficiencia global.

Tabla 7
Resultados y objetivos DEA Global.

3.5. Análisis de correlación

A continuación, se ha realizado un análisis de correlación de Pearson para los cuatro modelos DEA, como se puede observar en la Tabla 8.

Tabla 8
Análisis de correlación de los cuatro modelos DEA.

El coeficiente de correlación lineal de Pearson nos muestra que existe una correlación positiva y alta entre el modelo el modelo DEA 2 y 4 (0,7048), el modelo DEA 1 y 2 (0,7085), y finalmente, y en mayor medida, entre el modelo DEA 3 y el 4 (0,7566), siendo las otras moderadas o bajas (DEA 1 versus DEA 3).

El objetivo general propuesto en este artículo ha sido el establecimiento de un ranking de eficiencia global de las cincuenta mejores universidades del mundo. En la definición de dicho concepto se ha tenido en cuenta las tres funciones básicas que desarrollan las universidades como son, las relacionadas con su actividad investigadora, su apoyo a la innovación empresarial y la mejora del grado de inserción laboral de sus egresados universitarios.

Con carácter previo se han realizado tres análisis DEA que han recogido específicamente tres variables outputs relacionadas con cada una de las funciones básicas, como son las extraídas del World's Most Innovative Universities, el Ranking Académico de las Universidades del Mundo –ARWU- y el QS Graduate Employability Rankings. De esta forma se han podido establecer tres tipos de ordenación de las DMU en función a su proximidad a una frontera de eficiencia parcial.

Posteriormente se ha aplicado el análisis envolvente de datos al concepto de eficiencia global, y que ha recogido tres outputs y se ha podido establecer un ranking.

En todo caso, los resultados obtenidos deben de ser interpretados con cautela, ya que son el resultado de haber definido una función de producción con esas tres variables output y cuatro variables inputs. Cualquier modificación en la definición de dicha función llevaría consigo que los resultados que arrojaría el modelo pudieran ser diferentes. El motivo de esta situación viene dado por el hecho de no poder establecer, de manera inequívoca, el proceso de conversión de variables inputs en outputs.

Los resultados aportados no solo arrojan una graduación universitaria en el nivel de eficiencia parcial y global. El análisis realizado ha permitido determinar para cada una de ellas los aspectos concretos que debería mejorar para alcanzar la condición de máxima eficiencia global.

Asimismo se ha establecido un análisis de correlación entre los resultados obtenidos de la aplicación DEA. En ellos ha quedado demostrada la relación positiva que existe entre el nivel de patentes universitarias y el nivel de publicaciones. Igualmente ha quedado demostrada la relación entre la función investigadora y la función de mejora del grado de ocupabilidad universitaria.

Finalmente destacar, por la importante función que desarrollan las universidades, la necesidad de seguir realizando este tipo de análisis. Básicamente en dos líneas de actuación. Por un lado, mediante estudios de tipo cuantitativo, para lo cual sería conveniente que las universidades pusieran a disposición de los investigadores mayor cantidad de información sobre la evolución de las variables inputs/outputs utilizadas en este tipo de investigaciones. Por otro, mediante el desarrollo de análisis cualitativos que permitiesen justificar los resultados obtenidos.

Abbott, Malcolm; Doucouliagos, Chris. “The efficiency of Australian universities: a data envelopment analysis”. Economics of Education review, v. 22(1), 2003, pp. 89-97. Recuperado de: https://www.sciencedirect.com/science/article/pii/S0272775701000681?via%3Dihub#!

Bartual, Amparo; Garrido, Ramón. “Análisis de la eficiencia y liderazgo de los puertos españoles por áreas geográficas”. Revista de estudios regionales, v. 91, 2011, pp. 161-184. Recuperado de: http://www.redalyc.org/html/755/75522233007/

Belmonte, Luís J.; Plaza, José A.  “Análisis de la eficiencia en las cooperativas de crédito en España. Una propuesta metodológica basada en el análisis envolvente de datos (DEA)”. Revista CIRIEC, v. 63, 2008, pp. 113-133. Recuperado de: http://www.redalyc.org/html/174/17412307005/

Blanco, Miguel; Bares, Lydia; Hrynevych, Oksana. “Ranking of global efficiency of the best universities in Europe”.  Marketing and Management of Innovations, v. 3, 2018, pp. 34-47. Recuperado de:  http://mmi.fem.sumdu.edu.ua/en/journals/2018/3/34-47

Charnes, Abraham; Cooper, William; Rhodes, Edwardo. “Measuring the efficiency of decision making units”. European journal of operational research, v. 2(6), 1978, pp. 429-444. Recuperado de:  https://www.sciencedirect.com/science/article/pii/0377221778901388#!

Charnes, Abraham; Cooper, William; Wei, Q. L; Huang, Zhang. “Fundamental theorems of nondominated solutions associated with cones in normed linear spaces”. Journal of Mathematical Analysis and Applications, v. 150(1), 1990, pp. 54-78. Recuperado de: https://ac.els-cdn.com/0022247X9090195L/1-s2.0-0022247X9090195L-main.pdf?_tid=54741e7c-35d7-4a47-80cb-955a9a2813df&acdnat=1540202795_9b2533f39b90c775e85907ec0af4fb42     

Emrouznejad, Ali; Yang, Guo-Liang. “A survey and analysis of the first 40 years of scholarly literature in DEA: 1978–2016”. Socio-Economic Planning Sciences, v. 61, 2018, pp.4-8. Recuperado de: https://www.sciencedirect.com/science/article/pii/S0038012117300174

Fernández, G. M. Q., Minaya, W. R. J. Medición de la Eficiencia Técnica en las Universidades Autónomas del Sistema Universitario Boliviano: Aplicación del Análisis Envolvente de Datos (DEA). Revista ESPACIOS, v. 38(45), 2017. Recuperado de:  http://www.revistaespacios.com/a17v38n45/a17v38n45p03.pdf

Johnes, Jill. “Measuring teaching efficiency in higher education: An application of data envelopment analysis to economics graduates from UK Universities 1993”. European Journal of Operational Research, v. 174(1), 2006, pp. 443-456. Recuperado de:  https://www.sciencedirect.com/science/article/pii/S0377221705002444

Johnes, Jill; Li, Yu. “Measuring the research performance of Chinese higher education institutions using data envelopment analysis”. China economic review, v. 19(4), 2008, pp. 679-696. Recuperado de: https://www.sciencedirect.com/science/article/pii/S1043951X08000679

Kuah, Tse; Wong, Yew. “Efficiency assessment of universities through data envelopment analysis”. Procedia Computer Science, v. 3, 2011, pp. 499-506. Recuperado de: https://ac.els-cdn.com/S187705091000459X/1-s2.0-S187705091000459X-main.pdf?_tid=142ea76c-b1c5-4b8a-96b2-7cadaf82b673&acdnat=1540201860_eca211ccfdbf33d2bad952bf2029d574

Martić, Milan; Novaković, Marina; Baggia, Alenka. “Data envelopment analysis-basic models and their Utilization”. Organizacija, v. 42(2), 2009, pp. 37-43. Recuperado de:  https://ideas.repec.org/a/vrs/organi/v42y2009i2p37-43n1.html

Pastor, José M. Eficiencia, cambio productivo y cambio técnico en los bancos y cajas de ahorro españolas: Un análisis de frontera no paramétrico, Valencia, Institut Valencià d'Investigacions  Econòmiques, 1995. Recuperado de:  https://web2011.ivie.es/downloads/docs/wpasec/wpasec-1995-09.pdf

Peñate, Y.; Rivero, J. L.;  Lozada, D. I. Análisis envolvente de datos (DEA): Un enfoque viable para la evaluación de la eficiencia docente e investigativa en las universidades ecuatorianas. Revista ESPACIOS, v. 38(30), 2017. Recuperado de:  http://www.revistaespacios.com/a17v38n30/17383013.html

Pino, José L.; Solís Francisco M.; Delgado, Mercedes; Barea Rosario del Carmen. “Evaluación de la eficiencia de grupos de investigación mediante análisis envolvente de datos (DEA)”. El profesional de la información, v. 19(2), 2010, pp. 160-167. Recuperado de:  http://hdl.handle.net/11441/44842

Sagarra, Martí; Mar-Molinero, Cecilio; Agasisti, Tommaso. “Exploring the efficiency of Mexican universities: Integrating data envelopment analysis and multidimensional scaling”. Omega, v. 67, 2017, pp. 123-133. Recuperado de:  https://www.sciencedirect.com/science/article/pii/S0305048316301530

Wolszczak-Derlacz, Joanna. “An evaluation and explanation of (in) efficiency in higher education institutions in Europe and the US with the application of two-stage semi-parametric DEA”. Research Policy, v. 46(9), 2017, pp. 1595-1605. Recuperado de: https://www.sciencedirect.com/science/article/pii/S0048733317301221

1. Facultad de Ciencias Económicas y Empresariales, Universidad de Cádiz, Profesor del Departamento Economía general, miguel.blanco@uca.es

2. Facultad de Ciencias Económicas y Empresariales, Universidad de Cádiz, Profesora del Departamento Economía general, lydia.bares@uca.es

3. Facultad de Ciencias Económicas y Empresariales, Universidad de Cádiz, Doctoranda del Departamento Economía general, o.hrynevych1988@gmail.com