ISSN 0798 1015

Vol. 40 (Number 9) Year 2019. Page 25

Managing of mathematics education with synergistic effects

Gestión de educación en matemáticas utilizando efectos sinérgicos

SMIRNOV, Eugeny I. 1; ZYKOVA, Tatyana V. 2; TIKHOMIROV, Sergey A. 3

Received: 21/11/2018 • Approved: 18/02/2019 • Published 25/03/2019

Contents

1. Introduction

2. Methodology and Technologies

3. Results

4. Conclusions

Acknowledgements

Bibliographic references

1. Introduction

Education space of Russia (especially mathematics education in both secondary school and university) is currently forerunning a revolutionary situation. Digitizing schools and universities has been declared the key trend of the Russian education and is aimed to provide answers to the “explosive” emergence of new competencies, changes in labor market and openness of the global information space. Young people of today have clearly become more intolerant of long-held education clichés and inflexible teaching. They are living a life in a more pragmatic way and prefer to get knowledge and competencies that would be useful in their future personal and professional life. At the same time, intellectual operations (understanding, concretion, abstraction, generalization, modeling, analogy, associations, etc.), which form universal learning activities, because of various external and internal reasons, have ceased to effectively develop in secondary school education. And then, we lose the role of mathematics education as one of the most effective tools for personal development and social transmission, despite having so many great examples of applying mathematics in real life, science and production. . Mathematical disciplines are isolated from each other and from natural-science and informational knowledge and work methods. It complicates students’ understanding multistage mathematical abstractions. It is sad because there are a lot of great advances and applications of mathematics in real life, science and technology. It will suffice to mention advances in fractal geometry ((B. Mandelbrot, 1983), (R.М. Crownover, 1995), (K.J. Falconer, 1990), (V.S. Sekovanov, 2016), et al.), chaos and catastrophe theories ((A.N. Kolmogorov), (V.I. Arnold, 1992), (R. Thom, 1989), et al.), fuzzy logic (( L. Zadeh, 1997), (А. Коufmann, 1977), (L.I. Kuncheva, 2004), et al.), coding theory ((C.E. Shennon, 1948), (D. Huffman, 1952), (R. Hill, 1986), (M. Stibel, 2005), et al.),  distribution theory ((L.  Schwartz, 1950), L.V. Sobolev, I.M. Gelfand, et al.), etc. It is managing education by means of computer and mathematical modeling that can motivate everyone to study mathematical disciplines. It will result in increasing interest in mathematics that develops theoretical thinking (comparison, analogy, analysis, synthesis, etc.) and dominating of logical reasoning. Children will be able to reason in a clear way, recognize and sum up, analyze and synthesize, and model. Today in individualized secondary mathematics education, as well as university ones, the principles of basic math concepts and procedures are almost ignored: derivative, area of surface, integral, measure and probability, etc. Taking this direction we will get the interaction of mathematical, informational, natural-science and humanistic cultures and the unity of math content. Computer-aided systems, frameworks and teaching products (MathLab, MatCad, GeoGebra, Autograph, ClassPad400, Qt Creator, etc.) are insufficiently used in mathematics at secondary school and university. They can be used not only as a user interface but also as symbiosis of mathematics and computer science that supports learning mathematics by means of visual modeling and interaction of mathematical, informational, natural-science and humanistic cultures. At the same time, obvious nonlinear nature in the structures of laws governing matter development, biological, social and personal processes, exponential information growth, emergence of social communication opportunities and information media availability determine the factors necessary to change educational paradigms not only in the direction of openness, informatization, individualization and social interactions, but also methods, technologies and processes of learning math content. At the end of the 20th century, the postnonclassical scientific worldview began to take shape as the paradigm effect of a set of theoretical and methodological guidelines based on the priority of self-organization processes of dynamic non-linear systems following coordinated actions of various basic factors  (H. Haken, T. Kun, B. Mandelbrot, I. Prigogin, (G.G. Malinetskiy, 2017), et al.). There should be synergy of mathematics education as a student can be involved in the process of self-organization and motivation. They can learn mathematical objects and procedures by understanding and learning modern advances in science. The special aspects and needs of current education development demonstrate that one of the efficient solutions of mathematics education development problems might be developing and implementing a synergistic paradigm at secondary school and university by creating an innovation complex of teaching, information and organization conditions in the context of the scientific technocratic and  human paradigm symbiosis. Synergy in mathematics education is “a symbiosis of nonlinear effects of a person’s self-organization and self-development through learning mathematics when complex stochastic cognitive  processes are fluctuated by various factors and basics in three contexts: conceptual (semiotic), procedural (simulation) and social” (E.I. Smirnov, 2016). The last research proved feasibility of conditions that would improve mathematics education and personal development by adapting modern science advances to secondary and university mathematics: information richness of learning motivational field (including secondary school and university digitalization processes), multiplicity of goal setting and search for bifurcation transitions in mathematical activity, fluctuation diversity of  parameterization and integration of mathematical, informational, natural-science and humanistic knowledge in constructing mathematical results in the form of attractors and basins of attraction of nonlinear transformations based on mathematical and computer modeling (including using neural networks and intelligent systems), interaction of cultures and network interaction on single communication platforms of research, taking into account the stochastic processes and generalization of results, setting up an experiment in mathematics and manifesting synergistic effects of personal development under the conditions of progress towards understanding the essence of mathematical objects and procedures. Today we are able to manage secondary school mathematics with synergetic effects and appropriately meet the challenges of mathematics education that correspond with each student’s needs in their personal development and mathematical and information competencies. There are technologies of students’ self-organization and interaction of cultures by developing a synergistic paradigm of learning mathematics in secondary school in the context of motivated, coherent and level revealing and creative overcoming of “problem areas” of mathematical activity. In view of the above, this becomes a national problem, the problem of Russia’s national security.

Philosophers of science, educators and psychologists (I. Kant, G.V. Hegel, I. Prigogin, H. Haken, V.V. Orlov, (A.N. Podiyakov, 2015), V.S. Stepin, I.S. Utrobin, H. Alven, T.S. Vasilyeva, et al.) convincingly showed that effective personal development occurs during getting complex knowledge (different levels of its complexity depending on students’ personal development, including inclusive education), creating situations of overcoming difficulties when getting knowledge and a single world view on the basis of a high degree of   deployment of students’ educational and professional motivation in a single network of interaction, autonomy and coherence. In complex cognition, the process of cognition itself "becomes a communication, a loop between cognition (a phenomenon, an object) and cognition of this cognition" (E. Morin). Then, learning mathematics can help solve the problem of a student’s self-organization and self-development. We should combine motivational, emotional-volitional, research, metacognitive, social and personal strategies of behavior to learn innovative math content on the basis of cultural interaction and a single efficient communication network (K. Mainzer, G .G. Malinetskiy, E. Morin, H. Haken, et al.). Along with (A.N. Podiyakov, 2015) we note the following features of solving complex problems in mathematics education:

● There is always a bit of uncertainty and unpredictability in the behavior and development of a complex dynamic system; it requires a variety of descriptions and solutions that differ from each other and complement each other; the concepts “loose” and “fuzzy”, built on the basis of empirical rather than theoretical generalizations are effective tools, too.

● A complex system is characterized by changes not only at the level of particular manifestations, but also at the level of its essence. In complex systems, effective rules (founding modes (E.I. Smirnov, 2012)) of a staged deployment of the essence can be distinguished, but they will inevitably be quite variable based on visual modeling (E.I. Smirnov, 1998) and fundamentally dependent on the context.

● Theoretical models of any level are fundamentally limited. To effectively study complex dynamic systems we need various search samples (test assessments, comparative analysis of particular manifestations, computer modeling, analogies, analysis by synthesis (S.L. Rubinstein, 1958)), etc. –  real interactions with the system, not just theoretical activity with its abstract models.

● To study a complex system we need to have variability in goal-setting which is ability to set various goals of different types and levels that can compete with each other. One of the main emotional states of a person studying complex systems is uncertainty, doubt, and willingness to accept two-fold (predictable and random) action results, etc.

● The results of a person’s interaction with a complex system cannot be completely predictable. Along with direct, predictable results, there is a variety of side, unpredictable products.

Managing synergy of mathematics education in school is possible and effective when characterizing, building hierarchies and actualizing the internal attributes (mechanisms) of self-organization of various types (conceptual – figurative-geometric, sign-symbolic, verbal, activity; procedural – methods, technologies, techniques, ideas, algorithms of cognitive activity, social – interaction of cultures, work in small groups, value systems, etc.) that manifest by passing bifurcation zones and form successful functioning of the system as the integrity of all the new levels of increasing complexity. Such mechanisms can be fractal structures, generalized constructs of “problem areas” of secondary school mathematics, regulatory systems of rules and values ​​in developing  mathematical activity, building interaction of cultures as a form of deployment of integrative processes, universal laws of constructing mathematical objects and procedures, etc. At the same time, integration of natural-science, humanitarian and mathematical cultures become actual by using information technologies, and teaching processes acquire a new quality: natural-science knowledge is enriched with a humanitarian aspect, humanitarian knowledge takes a scientific way for establishing the essence using the natural-science and mathematical apparatus and methods. One of the main means that generate synergy of mathematics education and define the tasks and direction of the present research is the processes of adapting modern advances in science to mathematics education in secondary schools and universities. The term “synergy” (synergeia (Greek) is a joint action, cooperation) was proposed in the late 1960s by the German theoretical physicist from Stuttgart (Germany) H. Haken (H. Haken, 1983). The synergy subject is complex self-organizing open systems that are far from equilibrium conditions (when non-linear exchange of matter, energy, information occurs). In philosophy, self-development is considered as part of the self-motion of complex systems (in particular, of a personality structure), which goes beyond self-active, spontaneous change and marks the transition to a higher level of its organization. The research and importance of self-organization in animated and inanimate nature through destruction and creation processes (chaos and order) showed that increase in complexity of open and non-equilibrium systems is not a destructive mechanism, but rather a necessary transition to a new level of development, more complex and ordered forms of organization, as well as educational structures. The most important problem of a student’s mathematics education is the question of literal perception of the learning material and the activity that leads to understanding amid high educational or professional motivation.

This conflict resolution is the key to overcoming the formalism in mastering mathematics, the negative phenomenon that has swept through both secondary and higher education in recent decades. Our functionaries find a way out of this situation by simplifying the content of mathematics education and strict ordering of mathematics learning processes (USE at different levels, differentiating procedures and unambiguous conclusions, guaranteed and predictable decisions and learning outcomes, lack of communication in open, stochastic and network communities, etc.). Any member of the public can already see the results of this approach to education (not just mathematics): level decrease of math culture, lack of schoolchildren’s intellectual development, the narrow focus of educational interests and loss of education values, the gap to global education systems and standards, which never happened half a century ago. The content of mathematics education in secondary schools and universities should have units of open, stochastic and nonequilibrium complex forms, means and structures, in conditions of collision and integration of diverse cultures and ensuring their interaction (of mathematical, humanitarian, natural-science, information cultures) and self-organization.

Implementing the declared concept is connected with students’ getting complex knowledge by mathematical and computer modeling in a rich information educational environment. An effective management tool of mastering complex knowledge might be the study and adaptation of modern advances in science to secondary school or university mathematics, the advances that are clearly and meaningfully presented in applications to real life, the development of other sciences, high technologies and industries.

The basic concept of managing students’ cognitive activity in the context of adapting modern advances in science is founding personal experience. What is the phenomenon of founding? Founding (Fundierung (German) is justification, basis) is the term used in phenomenology (and in other sciences) to describe relations of ontological justification. E. Husserl defines funded relation as follows: A is funded by B, if for its existence A essentially needs B, only in unity with which A can exist. Funded relation can be one-sided (A is funded in B) or two-sided (A and B are funded in each other). According to the phenomenological doctrine, all complex high-level acts and objectnesses are funded in original simple acts and objects. The concept of founding was first introduced into pedagogy by V.D. Shadrikov and E.I. Smirnov in 2002 (V. Shadrikov, et.al., 2002) as the process of creating conditions for gradual deepening school knowledge in the direction of forming an integrated system of scientific and methodological knowledge, as the process of forming an integrated system of professional and educational activities. Later the authors expanded the basic principle of founding personal experience from its present state to staged manifestation of the essence of the basic learning element for both school and university. The fundamental distinctive feature of the structure-forming principle of funding for professional education of a teacher is determining the basis for a spiral-like scheme for modeling students’ basic knowledge, skills and proficiency (including mathematics). The concept of founding enjoins the necessity according to which in the principal educational program of a university there should be courses and learning activities that form not only goal-setting, gaining, using and developing personal experience, but also proficiency in teaching, motivation and emotions, self-reflection and self-direction, self-evaluation and choice, intelligence and creativity. Therefore, the founding concept of developing a teacher’s personality is an effective mechanism for overcoming professional crises of becoming a teacher and updating the integrative links between science, professional education and school. Such effectiveness has been demonstrated by many years of experience in theoretical and empirical elaboration.

One of the crucial findings of the concept under consideration is moving from founding knowledge (an orientation basis of activity) to founding personal experience in learning mathematics on the basis of its current state. Considering the concept of founding by L.S. Vygotsky's cultural-historical paradigm leads to the need to design the staged deployment of integrative knowledge constructs and activity patterns in accordance with the existing state of experience and development of an individual's higher mental functions (social development) during studying. At the same time, we should diagnose the emergence of generalized constructs of the gained experience and the “increase” of personal characteristics in “the zones of proximal development” (L.S. Vygotsky's “chain of quality changes”) against joint activities of a teacher and a student in a clearly updated spiral or cluster format (individualization) of the processes of knowledge representation and work methods. The qualitative feature of a founding effect emergence in the deployment of funding spirals or clusters is “a priori” detecting and further updating the generalizations of essential connections not only in the processes, phenomena and facts considered during cognitive activity, but also in developing students’ mental processes and functions in “the zones of proximal development " (L.S. Vygotsky, 1962).

Thus, experience founding as an innovative mechanism for personal development and comprehension of the essence of a generalized construct of mathematics education during studying modern advances in science can run in three educational niches: the content of secondary school mathematics education, the adaptive process implementation technologies and the development of students’ personal qualities.

Psychologists and educators consider adaptive processes to be a dynamic complex of integrated interaction of internal results (a system of knowledge, skills, attitudes, values) and adequate mechanisms for adapting a personality to environment changes and outcomes of developing activity (Rean A.A., 2008), (Tolstykh YI, 2011), (Soroko SI, 2012). In our study, the phenomenon of adapting modern advances in science (as environment manifestations) to secondary school mathematics in the context of actualizing the mechanisms of a person’s adaptation and learning appears initially as a process and result of research of an unclear, fuzzy, uncertain state of a generalized construct essence and its individual qualitative manifestations). Further, in the process definition, adaptation acts in the context of adequate learning and funding the essence of complex knowledge as a generalized construct with the potential of a positive impact on the expansion of personal experience and qualities through interaction with learning elements in school, growth of a person’s educational and professional motivation and self-development with synergistic effects manifestations. According to the research results (S.N. Dvoryatkina & E.I. Smirnov, 2016), these will be 7 synergistic effects of adaptive process implementation: cognitive, motivational, professional, innovative, social, economic and spiritual and moral. At the same time, four stages of synergy manifestation in mathematics education by actualizing the interaction of mathematical, informational, natural-science and humanitarian cultures: preparatory, content-technological, assessing-correctional and generalizing-modifying were identified and characterized (V.N. Ostashkov & E.I. Smirnov, 2016). Figure 1 presents a coordination graph of stages of essence manifestation of a generalized construct of modern scientific knowledge in learning mathematics and stages of mathematics education synergy manifestations (E.I. Smirnov, 2017).

Fig. 1
Coordinated stages of essence manifestation of a
learning element and mathematics education synergy

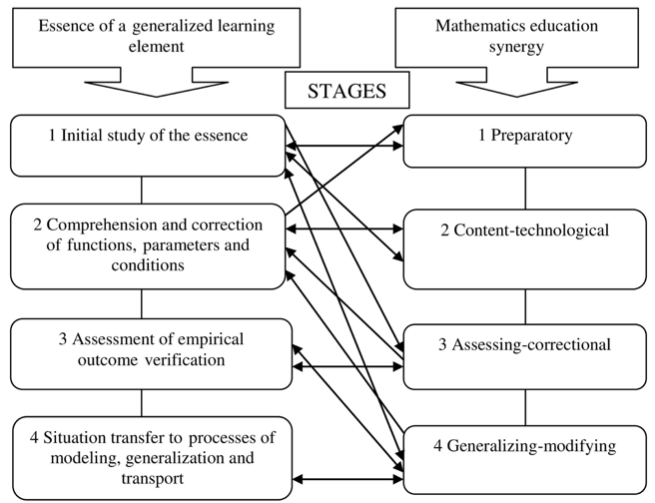
The type of modeling a generalized construct of modern scientific knowledge in mathematical activity based on the essence identified can be phenomenological and genetic. Following the theory of V.V. Davydov and D.B. Elkonin, we may note that the phenomenological type corresponds to the attributes and properties of empirical thinking formation, when there is sensation designation of object properties and their relationships, abstraction of these properties, combining them into classes and generalization based on the formal identity of their certain properties and their external changes in their interaction. The genetic type of modeling corresponds to the attributes and properties of theoretical thinking formation, when there is establishing of implicit hidden essential connections of objects, processes and phenomena of the role and functions of the relationship of components within the system, conditions of their origin and modification. After analyzing the essence identified and the most ideal object, an ascent to the true sensory-concrete whole takes place. Therefore, synergy manifestation technology in adapting modern advances in science to secondary school mathematics can be oriented, respectively, to the phenomenological or genetic type of identifying the essence of the generalized construct of scientific knowledge.

The cluster that controls funding a generalized construct with updating synergy attributes is a didactic model of funding synergy manifestations and adapting the generalized content essence of school mathematics “problem areas”, consisting of 4 stages: the initial study of the basic learning element essence at an intuitive visual level, the functional stage of comprehension and correction of functions, parameters and conditions of the dynamics and variability of process parameters, the operational stage of comprehension and generalization of the temporal and functional sequence of actions to learn the basic element essence, the assessment stage of empirical outcome verification quantitative and qualitative analysis of actions by means of mathematical modeling and computer-aided design, the integrative stage when the situation of learning the essence is transferred to processes of modeling, generalization and transport. Each stage is integrated with three spirals of funding the facilities for deploying and adapting the essence of the generalized construct: motivational and applied support for the processes of learning the essence; mathematical and computer modeling of synergetic effect manifestations and the stages of adapting the generalized construct to secondary school mathematics (motivational, of orientation-information richness, procedure-activity, assessing-correctional, and generalizing-modifying).

Our interaction with the world and other people activates our human potentials, which ensures our self-knowledge, self-regulation and self-actualization, thereby our personal development. Knowledge and values ​​that are mediated through learning mathematics can be accepted and become a student’s property when they are actively processed and learnt not by an individual, but become the content of communication and group activity, if they are integrated into all that information the group has. Thus, in the founding cluster performance structure, we pay attention to the problems of organizing students’ group interaction, which is the most important source of their self-actualization and development and the incentive for creative activity and further personal growth. When organizing group creative activities, it is necessary to create conditions for generating a plurality of solutions based on information richness, intellectual tension and a low degree of behavior regulation. So with group work, students have the opportunity to show over-situational activity and implement methods of enhancing creative thinking in mutual dependence, making the creative process dynamic (intuition, verbalization, visual modeling, formalization, reflection, verification) based on the synthesis of convergent and divergent thinking.

Fig.2
The founding cluster of synergy manifestations in adapting a
generalized construct of a problem area by fuzzy modeling

The technology of identifying and researching “zones of modern advances in science” as applied to learning mathematics allows us to design and implement the stages of adapting modern advances in science to the current state of schoolchildren’s mathematics experience, allows us to integrate knowledge from various fields of science in the context of school mathematics, creates a precedent for their research activity when working on a project (in small groups as well) and in the form of deploying individual learning routes, actualizes synergistic effects in mastering complex knowledge.

The conceptual constructs of the methods and stages of adapting generalized scientific knowledge to the current state of school mathematical knowledge and ways of students’ learning activities have been identified and mastered by means of mathematical and computer modeling.

New mathematical results have been identified and proved during mastering and researching the stages of essence manifestation of a generalized construct (spirals and clusters of knowledge founding have been built); coordination graphs of learning elements of secondary school mathematics and generalized construct elements have been made; effectiveness of managing mathematics education, visual modeling and the high level of schoolchildren’s learning motivation in the context of actualizing applications and specifying the essence of a generalized construct.

The synergy thesaurus of mathematics education has been reflected and actualized during students' research activities: fluctuations, bifurcation points, attractors, basins of attraction, etc.

The skills to adapt and develop in social communications and cognitive activity have been developed by interaction of mathematical, informational, natural-science, and humanitarian cultures.

The technology of researching “problem areas” in learning mathematics when actualizing modern advances in science with a synergetic effect is based on the staged phenomenological type of revealing the complex essence of a “problem area” generalized construct using mathematical and computer modeling with the interaction and unity of mathematical, informational, natural-science and humanitarian cultures.

The research was supported by Russian Science Foundation (project No. 16–18–10304).

1. Arnold, V.I. (1992). Catastrophe Theory, 3rd ed. Berlin: Springer-Verlag.

2. Bogun, V.V., Uvarov, A.D. & Smirnov, E.I. (2016). The synergy of mathematical education of teachers: Introduction to calculus. Yaroslavl: Kanzcler.

3. Crownover, R.M. (1995). Introduction in Fractal and Chaos. Jones and Bartlett Publishers.

4. Falconer, K.J. (1995). Fractal geometry: mathematical foundations and applications. England: John Wiley.

5. Dvotyatkina, S.N. & Smirnov, E.I. (2016) Evaluation of synergistic effects of knowledge integration and activity on the base of computer modeling. Modern information technologies and IT – education, Мoscow, МGU, 35–42.

6. Haken, H. (1983). Synergetics. Berlin-Heildelberg-New York: Springer.

7. Hill, R. (1986). A First Course on Coding Theory. Oxford: Clarendon Press.

8. Huffman, D.A. (1952). Method for the Construction of Minimum-Redundancy Codes. Proceedings of the IRE, 40 (9), 1098-1101.

9. Koufmann, A. (1977). Introduction a la theorie des sous-ensembles flous. Paris-New York-Milan: Masson.

10. Kuncheva, L.I. (2004). Combining Pattern Classifiers. Methods and Algorithms. New Jersey: Willey.

11. Mandelbrot, B. (1983). The Fractal Geometry of Nature. San-Francisco: W. H. Freeman.

12. Malinetskiy, G.G. (2017). Mathematical foundations of synergetics: Chaos, structures, computational experiment.  Moscow: URSS.

13. Ostashkov, V.N. & Smirnov, E.I. (2016). Synergy of education in the study of attractors and basins of nonlinear maps attraction. Yaroslavl Pedagogical Bulletin, Yaroslavl, no. 6, 146–157.

14. Podiyakov, A.N. (2015). Psychology of learning in conditions of novelty, complexity, uncertainty. Psychological research, 6-10.

15. Rean, A.A. (2008). Psychology of personality adaptation. SPb.: Prime-Euroznak.

16. Rubinstein, S. (1958). About Thinking and ways in its research. Moscow: USSR Academy of Science.

17. Schwartz, L. (1950). Theorie des noyaux. Proceedings of the International Congress of Mathematicians. Cambridge Massachusetts, 1, 220-230.

18. Shadrikov, V.D. et al. (2002). Preparation of the teacher of mathematics: Innovative Approaches. Edited by V.D. Shadrikov, Moscow: Gardariki.

19. Shennon, C.E. (1948). A Mathematical Theory of Communication. Bell System Technical Journal, 27, 379-423.

20. Sekovanov, V.S. (2016). Elements of the theory of discrete dynamic systems. SPb: Lan`.

21.  Soroko, S.I. (2012). Individual strategies of human adaptation in extreme conditions. Philosophy of human, 38, no. 6, 78-86.

22. Smirnov, E.I. (1998). Technology of visual modeling teaching of mathematics. Yaroslavl: YSPU.

23. Smirnov, E.I. (2012). Founding of the experience in vocational training and innovative activity of  teacher, Yaroslavl: Kancler.

24. Smirnov, E.I. (2017).Visual modeling of nonlinear dynamics of manifestation of essence of mathematical concepts and procedures. Proceedings of XIV International Kolmogorov Readings,  Koryazhma, 16-30.

25. Stiber, M. (2005). Spike Timing precision and neural error correction: local behavior. Neural Computation, 17 (7), 1577-1601.

26. Thom, R. (1989). Structural Stability and Morphogenesis: An Outline of a General Theory of Models. Reading, MA: Addison-Wesley.

27. Tolstykh, Y.I. (2011). Modern approaches to the category of "adaptive capacity". Izvestiya TulGU. Humanitarian Sciences, no. 1, 493-496.

28. Vygotsky, L.S. (1962). Thought and Language. Hanfmann E. (eds.). Cambridge, MA: M.I.T. Press.

29. Zadeh, L.A. (1997). Toward a theory of fuzzy information granulation and its centrality in human reasoning and fuzzy logic. Fuzzy Sets and Systems, 90 (2), 111–127. 

1. K.D. Ushinsky Yaroslavl State Pedagogical University, Yaroslavl, Russia, smiei@mail.ru

2. Siberian Federal University, Krasnoyarsk, Russia, zykovatv@mail.ru

3. K.D. Ushinsky Yaroslavl State Pedagogical University, Yaroslavl, Russia, satikhomirov@mail.ru