ISSN 0798 1015

Vol. 40 (Nº 8) Ano 2019. Pág. 13

Utilização do software Graph para ensino de coordenadas polares

Using the Graph software for teaching polar coordinates

SEMENSATO, M.T. 1; SILVA, F. D. 2; LOPES, M.R.C.M. 3; Castilho, A.S. 4

Recebido: 23/10/2018 • Aprovado: 08/02/2019 • Publicado 06/03/2019

Conteúdo

1. Introdução

2. Metodologia

3. Utilização do software Graph e discussões sobre a observação

4. Conclusões

Referências bibliográficas

1. Introdução

As instituições de ensino existentes atualmente no Brasil, com a sala de aula com carteiras organizadas em fileiras, utilização de lousa e giz, professor e livro didático, baseado nas memorizações, em que o professor muitas vezes é o único detentor do saber e os alunos meros receptores, é um modelo defasado que surgiu anteriormente ao século XIX e ainda perdura, salvo em raras exceções.

Refletindo sobre as evoluções científicas, tecnológicas e também a evolução humana, a sociedade que se configura exige que os ambientes educacionais, no âmbito da educação básica e no ensino superior, sejam do ponto de vista didático e pedagógico, inovadores e atualizados para que possam ir além dos conteúdos, formando indivíduos em saber científico, cultural e afetivo.

Em pleno século XXI, assim como Prenski (2001) afirma, os alunos são intitulados como “nativos digitais”, pois já nasceram imersos na era tecnológica e cada vez mais, acessam precocemente e com muita facilidade os meios digitais, como computadores, internet ou dispositivos móveis. Este fato evidencia a necessidade do modelo de escola de séculos passados adaptar-se aos alunos deste século. Neste contexto, a utilização de Tecnologias Digitais (TD) em sala de aula, como aliada para o ensino e aprendizagem, é uma opção para inspirar e guiar a prática dos professores, fazendo essa adaptação.

Buckingham (2008), afirma que as TD são inerentes à vida moderna, sendo sua utilização inevitável no ambiente educacional. No entanto, o professor precisa estar consciente de que a tecnologia precisa ser utilizada de forma adequada e respeitando as especificidades de cada público de estudantes, pois, apesar da familiaridade que os estudantes da atualidade possuem com a tecnologia, eles ainda sentem dificuldades em utilizá-la como aliada para a aprendizagem, ficando a responsabilidade aos professores, intitulados por Prenski (2001) como “imigrantes digitais” , fazerem a apropriação tecnológica necessária para utilizarem TD em suas práticas pedagógicas.

O próprio documento das Diretrizes Curriculares da Educação Básica do Paraná (2008) apresenta a preocupação e a necessidade de mudanças no ensino da matemática e, aponta a tecnologia como uma nova possibilidade na busca de um ensino e aprendizagem da matemática relacionada com o contexto em que os estudantes estão inseridos, além de ser uma ferramenta formadora de conceitos construtivos dentro de um contexto interdisciplinar (PARANÁ, 2008).

É preciso que as pessoas sejam conscientizadas do amplo universo que a Ciência e a Tecnologia incorporam e como os seus valores demonstram dramaticamente o seu grau de importância no avanço do conhecimento, do bem-estar e também dos riscos e prejuízos (BAZZO, 2010, p.31).

Na Educação Básica brasileira, as preocupações com o ensino e aprendizagem, na perspectiva da educação matemática, são amplamente discutidas na formação inicial pelas disciplinas pedagógicas, nas formações continuadas e também nos documentos normativos que amparam a educação básica. No entanto, muitas são as críticas dirigidas aos cursos superiores, no que diz respeito à ausência de didática por parte dos professores, pois muitos destes desconsideram a necessidade de formação específica para o exercício da docência, acreditam que o conhecimento específico adquirido na formação inicial e continuada é suficiente para assegurar o desempenho docente. (LOURENÇO; LIMA; NARCISO, 2016).

É evidente a necessidade de reforçar a dimensão pedagógica de nossa docência para adaptá-la às condições variáveis de nossos estudantes. Impõe-se a nós a necessidade de repensar as metodologias de ensino que propomos a nossos estudantes [...]; a necessidade de revisar os materiais e recursos didáticos [...]; de incorporar experiências e modalidade diversas de trabalho [...]. Este não é um trabalho fácil; ao contrário disso, exige uma reconstrução do perfil habitual dos professores universitários (ZABALZA, 2004, p.31; apud LOURENÇO; LIMA; NARCISO, 2016).

Considerando sobre esse reconstruir do perfil habitual do professor universitário, a desmotivação por parte dos alunos e os altos índices de reprovação na disciplina de Cálculo Diferencial e Integral II (CDI II), constatados nos anos de 2013 a 2016 na Universidade Tecnológica Federal do Paraná, campus Guarapuava, é que se desenvolveu uma prática pedagógica, utilizando o software Graph, como aliado no ensino e aprendizagem de coordenadas polares, na referida disciplina.

A utilização de TD, por meio do software Graph, foi uma alternativa encontrada para tentar amenizar as dificuldades de aprendizagem, falta de domínio dos conteúdos e dos conceitos básicos de matemática, da maioria dos acadêmicos dos cursos de graduação.

Essa pesquisa se desenvolveu, no segundo semestre de 2016 com os objetivos de utilizar o software Graph para que os discentesmelhorassem de forma significativa sua compreensão diante de alguns conteúdos previstos no programa  da  disciplina de CDI II e desenvolver um ambiente colaborativo dentro da sala de aula por meio de atividades em grupos nas quais os alunos fizessem parte da construção do conhecimento, abandonando a figura de ser passivo e receptor de conceitos e conteúdos prontos e acabados.

Metodologicamente esta pesquisa teve uma abordagem qualitativa, centrada no estudo de caso.

1.1. Referencial teórico

No processo de aprendizagem da matemática, vale salientar a importância do aprender fazendo, do aprender a aprender, das experiências que o aluno possui e de sua participação.

Quando se discute sobre tecnologias, destacam-se as quatro fases das TD; a primeira teve início nos anos 80, sendo predominantemente marcada pelo uso do software LOGO, a segunda fase é marcada pelo uso de softwares de geometria dinâmica e sistemas de computação algébrica, a terceira pelo uso da internet em cursos à distância, e a quarta pela utilização da internet rápida, que democratiza publicações de matérias digitais (BORBA; SILVA; GADANIDIS, 2014).

Na segunda fase, que teve início na década de 90, surgiram diversos softwares educacionais, os quais foram produzidos por empresas, órgãos governamentais e também por pesquisadores. Por causa da quarta e atual fase das TD que esses softwares, principalmente os livres, estão chegando ao conhecimento dos professores com potencialidades para o ensino. A partir desse momento, de acordo com os autores supracitados, os professores passaram a procurar cursos de formação a fim de dar suporte e descobrir alternativas para utilizar a tecnologia em suas aulas.

No entanto, é fato que nem todos os professores buscam por formação e alternativas de incorporarem as TD em suas aulas, pois assim como afirmam Garcia et al (2011) e Souto (2014) ainda há resistência de muitos professores em relação ao uso de TD.

O docente deve estar interessado em atualizar os meios metodológicos que auxiliam na prática de um ensino de qualidade. Se existem muitos meios e se o professor deve considerar os valores e a visão de mundo dos seus alunos, fica claro que as mudanças metodológicas e tecnológicas devem ser prioridades para melhorar o ensino (FLORES; RIBEIRO; ECHEVERRIA, 2017, p.4).

É preciso que as instituições de ensino percebam as transformações que as TD podem causar no cotidiano de seus cursos e alunos e, preocupem-se em incorporá-las, ou ficarão arcaicas e estagnadas (KENSKI, 2012).

É evidente que as TD por si só não são sinônimos de mudanças no ensino, porém, têm grande potencial para proporcionar possibilidades de apoio ao professor, caminhos e alternativas de novas formas de ensinar e aprender. Em consonância com Borba (2012), existem pesquisas sobre o uso TD em Educação Matemática há mais de 30 anos, porém este conjunto de pesquisas não é garantia da utilização da tecnologia digital nas aulas de matemática, pois isso envolve vários fatores, entre eles infraestrutura, investimentos financeiros e capacitação profissional.

Segundo Fiorentini e Lorenzato (2006) parece haver uma crença, entre alguns responsáveis pelas políticas educacionais, de que as novas tecnologias são uma panaceia para solucionar os males da educação atual. Essa é mais uma razão pela qual a comunidade de Educação Matemática vem investigando e discutindo seriamente a utilização de TD no ambiente educativo, de forma a contribuir com o ensino e aprendizagem da matemática.

Não precisamos romper com tudo, mas incorporar mudanças e supervisioná-las com equilíbrio e maturidade. Assim como Kenski (2012) aponta, com o avanço da tecnologia a forma como as pessoas vivem, informam-se e comunicam-se são modificadas, e essa modificação também precisa ocorrer nas metodologias de ensino adotadas pelos professores. No ensino superior, a implantação de TD em sala de aula, em particular de softwares educacionais, aliados a um encaminhamento metodológico adequado, tem grande potencial para substituir o ensino tradicional, proporcionando que o aluno se torne um ser ativo e participante da sua aprendizagem. Já o professor, que por muito tempo foi, e ainda em muitas universidades continua sendo, o único detentor do saber, com o apoio da TD pode atuar como facilitador, mediador e, incentivador  no processo de formação do acadêmico.

Essa pesquisa envolveu uma turma com 53 acadêmicos, dos cursos de Engenharia Civil e Engenharia Mecânica, da Universidade Tecnológica Federal do Paraná, no campus Guarapuava.

A fim de determinar as contribuições da utilização do software Graph no ensino de coordenadas polares, na disciplina de Cálculo Diferencial e Integral II, o processo metodológico adotado esteve pautado na pesquisa qualitativa.

Na abordagem qualitativa, a metodologia utilizada foi pesquisa de campo, pois:

“[...] É aquela utilizada com o objetivo de conseguir informações e/ou conhecimentos acerca de um problema, para o qual se procura uma resposta, ou de uma hipótese, que se queira comprovar, ou ainda, descobrir novos fenômenos ou as relações entre eles (MARCONI; LAKATOS, 2009, p. 188)”.

A pesquisa de campo se deu na forma de estudo de caso, pois, é o que ocorre quando há pouca possibilidade de controle sobre os eventos estudados e quando o foco de interesse é sobre fenômenos atuais, que só poderão ser analisados dentro de algum contexto de vida real (GODOY, 1995).

Assim como propõe o estudo de caso, esta pesquisa foi guiada pela observação detalhada da situação e do contexto em que está sendo feita a investigação, preocupando-se ao máximo em preservar o caráter unitário do objeto estudado (GIL, 2008).

A ação inicial para o desenvolvimento da pesquisa foi de revisão de literatura sobre as contribuições que a utilização de TD poderiam propiciar na aprendizagem.

Em seguida, houve uma conversa informal com os acadêmicos para investigar quais TD já haviam feito parte do processo de ensino e aprendizagem deles, no decorrer de toda vida escolar.

Na sequência, pensou-se em uma prática pedagógica que envolvesse um software educacional, optando-se pela escolha do Software Graph.

Sobre o Graph, de acordo com o site pandowan , é um aplicativo de código aberto usado para desenhar gráficos matemáticos em um sistema de coordenadas, o qual pode ser utilizado na versão em português.

O software Graph, permite trabalhar simultaneamente com várias representações de funções, como a simbólica, a gráfica e a tabular, o que contribui positivamente na visualização e aprendizagem de funções (BÁRRIOS, 2011).

A escolha pela utilização desse software deu-se pelo fato de ser um software livre, leve, de fácil manipulação e que permite boa visualização gráfica, sem contar que os alunos poderiam baixar com facilidade em seus computadores e também já estava instalado nos computadores do laboratório de informática da Universidade, para que fosse possível que todos os alunos tivessem acesso.

Em consonância com os apontamentos de Lima, Souto e Kochhann (2017):

(...) utilizar as tecnologias digitais no ensino implica em planejar, ter objetivos definidos e pensar qual a tecnologia apropriada para o alcance de tais objetivos. Em outras palavras, o uso a esmo ou domesticado não é suficiente, é necessário compreender como, quando e por que utilizá-las (LIMA, SOUTO e KOCHHANN, 2017, p. 149).

Dessa forma, visando quebrar o paradigma do ensino tradicional, o encaminhamento pedagógico por meio da utilização do software Graph, no decorrer de aulas de CDI II foi desenvolvido com a resolução de problemas envolvendo coordenadas polares, visando que a partir das explicações do professor da disciplina, os acadêmicos trabalhassem em grupos e, com o direcionamento do professor, interagissem entre si e com o docente, para que compreendessem de forma efetiva os conteúdos fazendo uso do pensamento abstrato . Preocupou-se em instigar os alunos a participarem ativamente da sua aprendizagem.

No decorrer do das atividades, objetivou-se oferecer caminhos propícios para desenvolver um cenário onde os acadêmicos realizassem testes, formulassem conjecturas, discutissem sobre elas, se familiarizassem com notações e confrontassem a forma geométrica e algébrica de resolver um mesmo problema, promovendo dessa forma um ambiente de discussões onde o aluno pudesse expor suas ideias e, em conjunto com os demais, fossem agentes indispensáveis na construção do conhecimento. Preocupou-se em encaminhar a prática dessa maneira, pois a partir das vivências, percebe-se que a maioria dos acadêmicos estão habituados a receber os conteúdos e conceitos prontos e acabados, e quando se deparam com algum exercício que destoa do que o professor fez em sala de aula, dizem que não sabem e abandonam o problema ou o procuram resolvido.

Para o feedback  da prática realizada, foi aplicado para os cursistas da disciplina um questionário semiestruturado com objetivo de fazer uma autoavaliação da prática pedagógica. Foi solicitado que o questionário fosse respondido de forma franca e que não houvesse identificação alguma, tudo isso, objetivando manter o mais fiel possível a real opinião dos acadêmicos.

Portanto, os instrumentos utilizados para coleta dos dados foram o questionário e a observação. A forma de observação utilizada foi a individual, que como o próprio nome indica, é aquela realizada pelo próprio pesquisador.

Para verificação se a prática realizada foi de fato satisfatória, também foram utilizadas as notas das avaliações individuais dos alunos no semestre de desenvolvimento da prática em comparação com as notas nos semestres anteriores.

No decorrer das aulas da disciplina de CDI II, várias atividades foram desenvolvidas com a utilização do software Graph, destas, duas são citadas no corpo deste artigo.

Das vivências em sala de aula, foi possível perceber que ao introduzir um novo sistema de coordenadas, como o sistema de coordenadas polares, os alunos de maneira geral apresentavam dificuldades significativas na interpretação de funções polares e problemas nos quais  é necessário calcular comprimentos, intersecções e principalmente área entre curvas polares, isto porque estão familiarizados a trabalhar apenas com o sistema de coordenadas cartesianas utilizada na educação básica.

Interpretar geometricamente uma curva dada em coordenadas polares envolve conhecimento de trigonometria, conteúdo que normalmente não dominam, uma vez que essas coordenadas são dadas por meio de raio e ângulo. Quando os acadêmicos se deparam com um problema dessa natureza, inicialmente tentam converter essa curva polar em uma curva expressa em coordenadas cartesianas, porém para algumas curvas essa conversão não é trivial. A falta de domínio gera a dificuldade que é agravada nos problemas como cálculo de área e comprimento dessas curvas. Diante dessas dificuldades, vários alunos abandonam o problema.

Dificuldades desse gênero podem ser amenizadas com o auxílio de um software educacional, como por exemplo o Graph. Ressalte-se, no entanto, como afirma Garcia et al (2011), que o uso da TD apenas como uma ferramenta, implica um risco de mantermos uma prática tradicional.  Para que isso não acontecesse, preocupou-se além da utilização do Graph, conduzir o encaminhamento metodológico diferente do habitual, propondo que os alunos trabalhassem em grupos, o que também facilitaria a interação entre eles.

Após a introdução do conteúdo de coordenadas polares em sala de aula, utilizando lousa, giz e o software Graph, foi proposto aos estudantes que em grupos de três alunos, realizassem uma Atividade Prática Supervisionada (APS), que constava de exercícios que deveriam ser resolvidos em seus cadernos, algebricamente, e exercícios que deveriam ser resolvidos, geometricamente, com o auxílio do software Graph. O objetivo da APS era que os alunos tivessem iniciativa, autonomia e explorassem as potencialidades do Graph para comparar os resultados obtidos algebricamente, resolvidos de forma tradicional em seus cadernos, com os resultados obtidos geometricamente, observando a interface do software, e discutissem entre si os comparativos dessas duas práticas. A APS também continha alguns exercícios que envolviam área entre curvas polares que exigiam interpretação mais elaborada do problema, uma vez que o software nem sempre calcula automaticamente essa área.

 Na sequência foi solicitado que resolvessem o mesmo exercício, porém, utilizando o software. Ao plotar as duas curvas no Graph, como segue na Figura 1, os alunos perceberam que existem três pontos de intersecção ao invés de dois.

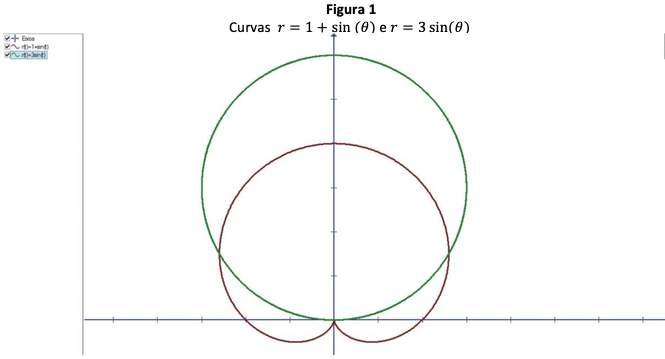
Fonte: Print screen da aplicação no software Graph

Após analisarem as curvas plotadas começaram a surgir perguntas: “Fizemos errado professor?” “Será que esquecemos de algo?” “Será que o Software está plotando errado?” “Por que isso está acontecendo?”.

Como o objetivo era fazer com que os alunos pensassem e refletissem sobre o conteúdo para que juntos encontrassem uma explicação correta do surgimento desse terceiro ponto, preocupou-se em instigá-los, por meio de questionamentos, para que justificassem esse fato e não simplesmente esperassem que o professor desse a resposta.

Voluntariamente, os alunos refizeram os cálculos algébricos e após perceberem que não haviam cometido erros, surgiram discussões entre os trios. Intrigados com a presença desse novo ponto de interseção, alguns acadêmicos, procuraram outros exemplos para analisar se este fato também ocorria. Somente após várias discussões concluíram que o ocultamento do terceiro ponto de interseção, quando fizeram os cálculos sem auxílio do Graph, ocorre devido à origem do sistema não ter uma única representação em coordenadas polares que satisfaça ambas as equações. Surgiu então a oportunidade para que o professor explicasse que no sistema de coordenadas polares, um ponto tem infinitas representações.

Um fato que chamou bastante atenção neste exercício, é que após os acadêmicos terem justificado assertivamente a divergência de soluções, eles ainda se preocuparam em explicar para seus colegas que não haviam entendido.

Nos grupos formados com objetivos educacionais, a interação deverá estar sempre provocando uma influência recíproca entre os participantes do processo de ensino, o que me permite afirmar que os alunos não aprenderão apenas com o professor, mas também através da troca de conhecimentos, sentimentos e emoções dos outros alunos. (VEIGA, 2000, p.105).

Esse fato indica um efeito positivo do encaminhamento metodológico adotado, pois a partir desse momento vários acadêmicos começaram a refletir sobre a situação problema, abandonando a reprodução mecânica de passos.

Vale observar que o conhecimento dos pontos de intersecção, diferentemente de problemas de área em coordenadas cartesianas, não garante o cálculo da área desejada sem a interpretação geométrica do problema. O desconhecimento desse fato levou alguns acadêmicos ao erro. Alguns alunos resolveram o exercício somente algebricamente, enquanto que outros resolveram com o auxílio do software, no entanto ao compararem as soluções entre os grupos houve divergência nas respostas. Neste momento, mediados pelo professor, os acadêmicos foram orientados a discutirem entre os grupos para analisarem qual solução era a correta.

Nas discussões entre os grupos, os acadêmicos que resolveram apenas algebricamente foram convencidos pelos demais que não conseguiriam calcular diretamente, com uma única integral, a área desejada.

Fonte: Print screen da aplicação no software Graph

-----

 Fonte: Print screen da aplicação no software Graph

Por meio do Graph os acadêmicos identificaram qual região deveriam calcular a área (Figuras 2 e 3).  Alguns acadêmicos perceberam que existe uma simetria nessa região, o que pode simplificar o processo. Vale ressaltar, que vários deles afirmaram não terem percebido a simetria quando trabalharam algebricamente.

Fonte: Print screen da aplicação no software Graph

-----

Fonte: Print screen da aplicação no software Graph

Somando as duas áreas e multiplicando por dois, devido à simetria, obtiveram a área desejada.

Constatou-se, que no caso do estudo de problemas que envolvem coordenadas polares, o professor somente precisa direcionar um encaminhamento metodológico coerente com os conteúdos trabalhados, e que seus alunos conseguem de forma colaborativa, por meio de discussões em grupos, construir o conhecimento matemático dando significado ao que antes era abstrato.

O trabalho em grupo torna o ensino mais crítico e criativo, no qual “tanto o professor quanto o aluno deixam de serem sujeitos passivos para se transformar em sujeitos ativos, capazes de propor ações coerentes que propiciem a superação das dificuldades detectadas” (Veiga, 2000, p. 104).

Fonte: Print screen da aplicação no software Graph

Ainda foi possível detectar, por meio de comentários dos próprios acadêmicos durante as aulas, que ficou claro para eles que a mesma curva por vezes é mais facilmente representada em um sistema de coordenadas polares do que em sistema de coordenadas cartesianas, como exemplo, destaca-se o comentário de um dos acadêmicos, que mencionou que a equação cartesiana x² + y² = 1, que representa uma circunferência centrada na origem com raio 1, é muito mais simples escrita da forma  r =1  em coordenadas polares.

Diante do observado, e comparando com a disciplina ministrada em semestres anteriores sem utilização de softwares matemáticos e trabalho em grupo, foi possível constatar que grande parte dos acadêmicos, ao se deparar com o sistema de coordenadas polares e a lei de formação de curvas em coordenadas polares, sente dificuldade em entender o que está sendo estudado, fazer uso do pensamento abstrato e compreender a diferença entre curvas cartesianas e curvas polares. O software, por meio da metodologia adotada, possibilitou que o conteúdo de coordenadas polares fosse compreendido de uma maneira mais simples, clara e atrativa. Além disso, constatou-se que o rendimento na avaliação do referido conteúdo teve melhora significativa uma vez que a média de notas da turma aumentou em 31,5% referente à mesma avaliação feita no semestre anterior, sem a utilização do software Graph e a metodologia adotada.

Assim como versam sobre o assunto Flores, Ribeiro e Echeverria (2017) observou-se que os acadêmicos demonstram interesse espontâneo em utilizar ferramentas tecnológicas no ensino, pela influência imperativa e cotidiana do uso de tecnologia na sociedade atual. Contatou-se que trabalhando em grupos os alunos permaneceram mais motivados, demonstraram mais iniciativa e exploraram novas possibilidades, buscando inclusive resolver com o software problemas que nem constavam na APS.

Além disso, acadêmicos criaram um hábito de verificar geometricamente se os exercícios resolvidos algebricamente estavam corretos, antes mesmo de verificar se a resposta condizia com a informada no final das listas de exercícios, ou no final do livro utilizado na disciplina.

3.1. Opinião dos acadêmicos a respeito da utilização do software Graph

Por meio da observação constatou-se os resultados positivos da pesquisa, no entanto, preocupou-se também em fazer uma autoavaliação da prática pedagógica utilizada, a fim de fazer um feedback levando em consideração a opinião dos acadêmicos.

 Foi utilizado um questionário semiestruturado, composto de perguntas abertas, as quais os acadêmicos responderam após o término da referida APS.

Mediante as respostas, vale fazer algumas considerações como, por exemplo, destacar que dos 53 alunos, 36 nunca haviam utilizado o software Graph ou qualquer outro similar, o que apresenta um número significativo se levarmos em consideração que 70% dos alunos passaram toda a vida escolar sem ter contato com ferramentas tecnológicas desse gênero no ambiente de ensino e aprendizagem.

Outro aspecto importante é que quando indagados se o software ajudou na compreensão do conteúdo, a resposta foi 100% afirmativa. Observe algumas respostas elencadas a seguir:

Acadêmico 3 - A ajuda gráfica ajuda enxergar melhor as dificuldades e a termos a ideia de que esse estudo não é em vão.

Acadêmico 8 - Sim, no início dos exercícios de coordenadas polares eu estava fazendo errado, foi no Graph que entendi como resolvia, e assim entendi a lógica dos exercícios.

Acadêmico 12 - Sim, tenho uma dificuldade pessoal em achar os intervalos de integração, ao meu ponto de vista o software ajudou bastante nisso.

Acadêmico 23 - Sim, o Graph ajudou a visualizar o que ocorre com certas funções principalmente quando mudamos algum coeficiente ou algo do tipo.

Acadêmico 41 - Com certeza, foi uma aplicação muito proveitosa e produtiva além da facilidade e eficiência.

Analisando as respostas dos acadêmicos reafirma-se o já observado durante a realização da APS, que a utilização do software Graph contribuiu significativamente para compreensão do conteúdo e, além do professor, também observaram nitidamente suas dificuldades e que conseguem superá-las utilizando um software e trabalhando em grupos.

Destacaram-se algumas respostas obtidas quando indagados se achavam que poderia melhorar a aprendizagem se houvesse a utilização de ferramentas tecnológicas como apoio pedagógico nas disciplinas que cursaram.

Acadêmico 14 - Sim, é necessário aprender a utilização dessas ferramentas principalmente nos dias atuais onde praticamente tudo é feito com o auxílio de computadores.

Acadêmico 23 - Sim, pois a interação com esses tipos de recursos prende mais a atenção, ajudando a manter o foco nos estudos fora de sala.

Acadêmico 27 - Totalmente, tais ferramentas ajudam demais no esclarecimento da matéria, tornam o abstrato em algo de fácil entendimento.

Acadêmico 38 - Sim, o uso de ferramentas tecnológicas trás uma melhor compreensão sobre o conteúdo a saber, pois as teorias tendem a cansar muito o aluno e com isso uma ferramenta que ele pode aplicar seus conhecimentos vem a facilitar e abrir a mente nos estudos.

Acadêmico 50 - Sim, pois torna a teoria em algo mais palpável, ficando mais fácil e mais interessante de estudar o conteúdo.

Fica evidente que a utilização de softwares educacionais deixa o conteúdo mais interessante e atrativo para os acadêmicos, aumentando a motivação e melhorando a compreensão de conteúdos matemáticos que são ensinados de forma tradicional.

Foi possível constatar no desenvolvimento dessa pesquisa, a qual se valeu da utilização do software Graph no ensino de coordenadas polares na disciplina de CDI II, que quando o aluno faz parte de maneira ativa do processo de ensino e aprendizagem, sente-se mais motivado e desafiado, mostrando interesse em descobrir coisas novas e estabelecer relações com o conteúdo que está sendo abordado em sala de aula.

O Graph contribuiu significativamente para que os acadêmicos conseguissem perceber os próprios erros cometidos algebricamente. Além disso, problemas que antes eram abandonados por falta de visualização gráfica, agora foram facilmente resolvidos, mesmo que algebricamente, quando o software não calculava. Notou-se ainda, que mesmo com o recurso gráfico, alguns alunos não abandonaram o estudo algébrico, pois mesmo os problemas resolvidos geometricamente foram conferidos algebricamente por vários acadêmicos.

Em relação à mesma disciplina ministrada no semestre anterior, a qual foi trabalhada de forma tradicional, utilizando aulas expositivas e fazendo uso somente de lousa e giz, foi possível perceber que a quantidade de exercícios resolvidos pelos alunos quando submetidos ao contato com o software foi significativamente maior do que a quantidade feita pelos alunos do semestre anterior. Isso mostra que a utilização de TD como prática pedagógica desperta maior interesse dos alunos pelo conteúdo. Além disso, destaca-se que esses alunos obtiveram notas relativamente maiores nas avaliações do que os alunos no semestre anterior.

Após a prática realizada, durante o restante do semestre, os acadêmicos buscavam pelo professor durante os horários de atendimento ao aluno, interessados em saber como poderiam utilizar outras funções do software para contribuir com a aprendizagem de outros conteúdos da disciplina CDI II e até mesmo de outras disciplinas. Constatou-se também que eles buscavam o software para verificação de resultados de exercícios que faziam algebricamente, antes mesmo de buscarem pelo gabarito dos exercícios. Essa nova postura dos acadêmicos, evidência positiva mudança de hábito no estudo de conteúdos matemáticos.

Em relação aos relatos dos alunos, ficou evidente que a maioria nunca teve contato com ferramentas tecnológicas nas disciplinas de matemática e que é unânime a satisfação com a implementação da tecnologia relatada neste artigo.

BÁRRIOS, A. F. R. (2011). Funções usando o software Graph: um estudo com alunos de um curso de educação e formação (tipo 2). (Dissertação de Mestrado em Educação). Universidade de Lisboa, Instituto de Educação, Lisboa.

BAZZO, W. A. (2010). Ciência, tecnologia e sociedade: e o contexto da educação tecnológica. 2.ed.rev.e atual. Florianópolis: Ed. da UFSC.

BORBA, M. C. (2012). Humans-With-Media and continuing education for mathematics teachers in online environments. ZDM Mathematics Education. Springer: Berlin.

BORBA; M. de C.; SILVA, R. S. R.; GADANIDIS, G. (2014). Fases das tecnologias digitais em Educação Matemática: sala de aula e internet em movimento. Belo Horizonte: Editora Autêntica.

BUCKINGHAM, D. (janeiro, 2008). Aprendizagem e cultura digital. Revista Pátio,  XI(44), Recuperado de https://www.academia.edu/2748122/Aprendizagem_e_cultura_digital.

FIORENTINI, D.; LORENZATO, S. (2006). Tendências temáticas e metodológicas da Pesquisa em Educação Matemática. In: Investigação em educação matemática; percursos teóricos e metodológicos. Campinas, SP: Autores Associados.

FLORES, A. D. M.; RIBEIRO, L. M.; ECHEVERRIA, E. L. A tecnologia da informação e comunicação no ensino superior: Um olhar sobre a prática docente. Revista Espacios. Vol 38, ano 2017,  n. 5, p. 17-31. Retirado de: https://www.revistaespacios.com/a17v38n05/a17v38n05p17.pdf

GARCIA, M. F. G. et al. (janeiro/abril 2011). Novas competências docentes frente às Tecnologias Digitais Interativas. Revista Teoria e Prática da Educação, (vol. 14, n.1, p. 70-87).

GODOY, A. S. (1995). Pesquisa Qualitativa Tipos Fundamentais. RAE – Revista de Administração de Empresas, São Paulo, (vol. 35, n. 3, p. 20-29, 1995).

KENSKI, V. M. (2012). Educação e Tecnologias: o novo ritmo da informação. 8. ed. Campinas (SP): Papirus.

LIMA, V. S. A.; SOUTO, D. L. P.; KOCHHANN, M. E. R.. (julho/dezembro 2017). Tecnologias digitais no ensino superior: Um zoom. Revista Prática Docente, Confresa, (vol 2, n. 2, p. 138-157). Recuperado de: http://periodicos.cfs.ifmt.edu.br/periodicos/index.php/rpd/issue/view/3/showToc.

MARCONI, M. A.; LAKATOS, E. M. (2009). Fundamentos de Metodologia Científica. 6ª Edição. São Paulo: Atlas.

PARANÁ, SEED. (2008). Diretrizes curriculares de matemática para a educação básica: Matemática. Curitiba.

PIAGET, J. (2003). A construção do real na criança. Editora Ática, São Paulo, SP.

PRENSKI, M. (outubro 2001). Digital Natives, Digital Immigrants. MCB University Press, (vol. 9, n. 5).

SOUTO, D. L. P. (2014). Transformações expansivas na produção matemática on-line 1.ed. São Paulo: Cultura Acadêmica.

VEIGA, I. P. A. (2000). O seminário como técnica de ensino socializado. In: Veiga, I.P. A. (org). Técnicas de ensino: Por que não?. Campinas: Papirus

1. Universidade Tecnológica Federal do Paraná. E-mail de contato michelsemensato@gmail.com

2. Universidade Estadual do Centro-Oeste. E-mail de contato fran-damiani@hotmail.com

3. Universidade Estadual do Centro-Oeste

4. Universidade Tecnológica Federal do Paraná