

Vol. 40 (Nº 3) Año 2019. Pág. 22
CECHIN, Rafaela B. 1; CORSO, Leandro L. 2
Recibido: 30/08/2018 • Aprobado: 17/12/2018 • Publicado 28/01/2019
RESUMEN: Este trabajo presenta un estudio de Cadenas de Markov aplicada a la probabilidad de ocurrencia de terremoto. Para ello, se utilizó un conjunto de datos históricos de casi dos décadas, para cinco localidades en América del Sur. Los datos fueron divididos en seis bandas de magnitud, y fue posible mostrar que las mayores probabilidades están en la previsión de que un próximo terremoto tenga una magnitud entre 3 y 3,9, y también evaluar las probabilidades de eventos de mayores magnitudes. |
ABSTRACT: This work presents a Markov Chains study applied to the probability of occurrence of earthquake. To do this, a set of historical data of almost two decades was used for five locations in South America. Data were divided into six ranges of magnitude, and it was possible to show that the greatest probabilities are in the prediction that a next earthquake will have a magnitude between 3 and 3.9, and also to evaluate the probabilities of events of larger magnitudes. |
El movimiento de las placas tectónicas genera un acumulo de energía, y cuando éste es liberado, ocurre un terremoto, que provoca temblores y desplazamiento del suelo en la superficie terrestre y posibles tsunamis si el movimiento de las placas se da en el fondo oceánico. Por ser un desastre natural catastrófico, Asim et al. (2018) comentan que las previsiones de tales fenómenos son de gran relevancia, ya que pueden salvar vidas o incluso reducir las pérdidas financieras. Los autores resaltan que tales previsiones son un estudio desafiante y que ocurren desde hace más de un siglo. Es posible clasificar los enfoques de previsión de terremotos en tres categorías: investigaciones de precursores, metodología de inteligencia artificial, y métodos matemáticos y estadísticos. La metodología de este artículo pertenece a la última clasificación citada.
El concepto de Cadena de Markov, que pertenece al área de Investigación Operativa, es un análisis estadístico de un proceso, en el cual el estado futuro depende exclusivamente de su estado actual, y posee sus orígenes realizados por Andrei Markov en 1909. Cambios de estado del Estado sistema se llaman transiciones. Las probabilidades asociadas a varios cambios de estado se llaman las probabilidades de transición. El proceso se caracteriza por una matriz, donde presentan las probabilidades de transiciones de un estado inicial a otro.
El objetivo de este trabajo es calcular, utilizando Cadenas de Markov, la probabilidad de ocurrencia de un nuevo terremoto en América del Sur, enfocándose en cinco localidades, siendo ellas, Chile, Argentina, Colombia, frontera entre Chile y Argentina, y Perú. Además, se estudió la probabilidad de un tercer evento, dependiendo de dos anteriores.

Para alcanzar el objetivo propuesto para este estudio, la metodología elaborada fue dividida en tres etapas: recolección de los datos, elaboración de la matriz de transición y análisis de escenarios, conforme detallado a seguir.
En este estudio se utilizaron datos históricos de terremotos que ocurrieron en América del Sur. Fue posible recoger fecha, hora, la magnitud del terremoto, la profundidad y la latitud y longitud de donde ocurrió, y fueron obtenidos en la dirección electrónica de las Instituciones de Investigación Incorporadas para Sismología (en inglés, Incorporated Research Institutions for Seismology – IRIS). Las características y posibles consecuencias de cada intervalo de magnitud de la escala de Richter se describen en el Cuadro 1.
Cuadro 1
Características de cada intervalo de magnitud
Magnitud |
Características |
1 a 1.9 |
Micro terremotos, no sentido, excepto por pocos en condiciones favorables. |
2 a 2.9 |
Sentido sólo por algunas personas en reposo, especialmente en los pisos superiores de los edificios. Los objetos delicadamente suspendidos pueden oscilar. Ningún daño a los edificios. |
3 a 3.9 |
Sentido notablemente por personas dentro de casa, especialmente en los pisos superiores de los edificios, pero rara vez causa daños. Muchas personas no lo reconocen como un terremoto. Los automóviles a motor pueden oscilar ligeramente. Vibración similar al paso de un camión. |
4 a 4.9 |
Sentido por la mayoría de las personas en el área afectada, muchos despertaron. Agitación notable de objetos internos y ruidos chocando, con paredes haciendo sonido de agrietado. Algunos platos, ventanas rotas, y objetos inestables derribados. Los relojes de péndulo pueden detenerse. Sensación como el camión pesado que alcanza el edificio. Los coches estacionados se agitaron notablemente. Generalmente no causa ningún daño grave. |
5 a 5.9 |
Sentida por todos, muchos asustados. Algunos muebles pesados se mueven. Daños leves en edificios de buen diseño y construcción; de la misma forma que en la mayoría de los casos. daños considerables en estructuras mal construidas o mal proyectadas; algunas chimeneas pueden romperse. |
6 a 6.9 |
Daños leves en estructuras especialmente proyectadas; daños considerables en edificios comunes, con colapso parcial; daños grandes en estructuras mal construidas. Caída de chimeneas, pilas de fábrica, columnas, monumentos, paredes. Muebles pesados vieron. Sentido en áreas más amplias, hasta cientos de kilómetros del epicentro, con fuerte agitación en el área epicentral. |
7 a 7.9 |
Causa daños graves a la mayoría de los edificios, algunos con colapso total o parcial. Las estructuras bien proyectadas también pueden dañarse. Se siente a grandes distancias, con grandes daños limitados a 250 km del epicentro. Los rieles pueden doblarse. |
8 a 8.9 |
Pocas estructuras, si alguna (albañilería), permanecen en pie. Causará daños moderados a pesados a edificios resistentes a terremotos. Damnificando grandes áreas. Se siente en regiones extremadamente grandes. Puentes destruidos, rieles muy doblados. |
Hasta de 9 |
Cerca de destrucción total - daños gravísimos y colapsos en edificios. Los daños y los temblores pesados se extienden a lugares distantes. Cambios permanentes en la topografía del suelo. Objetos jugados en el aire. |
Fuente: Adaptado del Departamento del Interior de EUA (1997)
Como se observa en el Cuadro 1, es a partir de la magnitud 3 que los terremotos son perceptibles a las personas, por lo que se seleccionaron solamente los terremotos que tuvieron una magnitud mayor o igual a 3 para este trabajo. Los eventos son referentes al 1 de enero de 2000 al 7 de abril de 2018. Dentro de este período de tiempo, se contabilizaron 6.672 días, en los cuales 6.630 ocurrió al menos un terremoto en América del Sur, representando el 99,37% de los días. Durante el período de análisis se produjeron más aproximadamente 78.760 terremotos mayor o igual a 3 grados en la escala de Richter. El Cuadro 2 presenta la cantidad de terremotos correspondiente a cada intervalo de magnitud.
Cuadro 2
Cantidad de terremotos para cada intervalo de magnitud
Intervalo de magnitud |
Cantidad de datos |
% |
3 a 3.9 |
52.321 |
66,43% |
4 a 4.9 |
23.526 |
29,87% |
5 a 5.9 |
2.654 |
3,37% |
6 a 6.9 |
231 |
0,29% |
7 a 7.9 |
27 |
0,03% |
8 a 8.9 |
5 |
0,01% |
9 a 10 |
0 |
0,00% |
Total |
78.764 |
100% |
Fuente: Elaborado por los autores (2018)
El Cuadro 3 se presenta la cantidad de terremotos separados por intervalo de magnitud respectivamente al lugar de ocurrencia, con relación a los lugares destacados por el IRIS.
Cuadro 3
Cantidad de terremotos en relación con el lugar de ocurrencia
Localidad |
Intervalo de magnitud |
Total |
|||||
3 a 3.9 |
4 a 4.9 |
5 a 5.9 |
6 a 6.9 |
7 a 7.9 |
8 a 8.9 |
||
Archipiélago Juan Fernández |
1 |
4 |
2 |
0 |
0 |
0 |
7 |
Argentina |
9976 |
4502 |
539 |
52 |
7 |
0 |
15076 |
Bolivia |
1073 |
672 |
68 |
15 |
0 |
1 |
1829 |
Brasil |
83 |
77 |
24 |
5 |
2 |
0 |
191 |
Chile |
28765 |
16052 |
2568 |
175 |
19 |
4 |
47583 |
Colombia |
6298 |
2728 |
330 |
20 |
5 |
0 |
9381 |
Dorsal Meso Atlántico |
179 |
642 |
200 |
12 |
0 |
0 |
1033 |
Ecuador |
2010 |
5019 |
220 |
31 |
3 |
0 |
7283 |
Frontera entre Chile y Argentina |
8429 |
2495 |
213 |
16 |
0 |
0 |
11153 |
Frontera entre Chile y Bolivia |
3598 |
1837 |
249 |
6 |
0 |
0 |
5690 |
Frontera entre Colombia y Ecuador |
138 |
188 |
5 |
1 |
1 |
0 |
333 |
Frontera entre Perú y Bolivia |
543 |
439 |
58 |
6 |
0 |
0 |
1046 |
Frontera entre Perú y Brasil |
174 |
376 |
81 |
12 |
4 |
0 |
647 |
Frontera entre Perú y Ecuador |
442 |
1014 |
95 |
8 |
0 |
0 |
1559 |
Guyana |
0 |
3 |
1 |
0 |
0 |
0 |
4 |
Guyana Francesa |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
Islas Galápagos |
8 |
6 |
0 |
0 |
0 |
0 |
14 |
Islas Georgias del Sur |
5 |
34 |
10 |
1 |
0 |
0 |
50 |
Islas Malvinas |
1 |
28 |
11 |
0 |
0 |
0 |
40 |
Mar de Scotia |
0 |
1 |
2 |
0 |
0 |
0 |
3 |
Océano Atlántico |
4 |
33 |
19 |
4 |
0 |
0 |
60 |
Océano Pacífico |
5 |
14 |
2 |
0 |
0 |
0 |
21 |
Paraguay |
1 |
1 |
2 |
0 |
0 |
0 |
4 |
Pasaje de Drake |
1 |
3 |
0 |
0 |
0 |
0 |
4 |
Perú |
2313 |
4704 |
1088 |
66 |
9 |
2 |
8182 |
Tierra del Fuego |
0 |
5 |
0 |
0 |
0 |
0 |
5 |
Trinidad |
826 |
117 |
17 |
2 |
0 |
0 |
962 |
Uruguay |
0 |
2 |
0 |
0 |
0 |
0 |
2 |
Venezuela |
2544 |
643 |
76 |
4 |
0 |
0 |
3267 |
Fuente: Elaborado por los autores (2018)
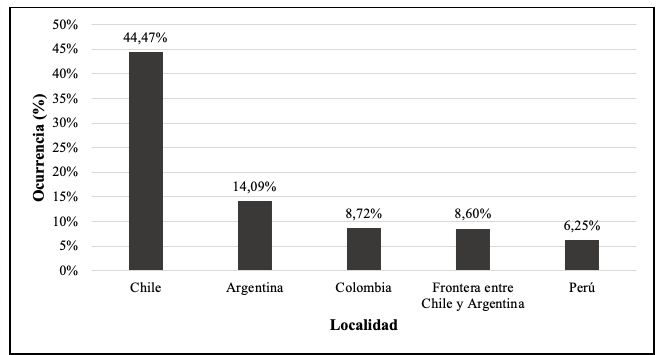
Con el Cuadro 3, es posible percibir que las cinco localidades con más ocurrencia de terremoto son: Chile, Argentina, Colombia, frontera entre Chile y Argentina, y Perú, representando más del 80% de los datos, como muestra la Figura 1.
Figura 1
Cinco localidades con más ocurrencia de terremotos
Fuente: Elaborado por los autores (2018)
También fue cotejada la información detallada de que ocurrirá el terremoto, conforme registrado no Cuadro 4 .
Cuadro 4
Cantidad de terremoto en relación con la profundidad
Profundidad (km) |
Cantidad de datos |
% |
0 a 32,9 |
28913 |
36,71% |
33 a 69,9 |
14800 |
18,79% |
70 a 149,9 |
23422 |
29,74% |
150 a 299,9 |
11295 |
14,34% |
300 a 499,9 |
70 |
0,09% |
500 a 800 |
264 |
0,34% |
Fuente: Elaborado por los autores (2018)
El Cuadro 5 muestra la cantidad de terremotos de cada intervalo de magnitud, respectivamente, para el intervalo de profundidad.
Cuadro 5
Cantidad de terremoto por magnitud y profundidad
Intervalo de magnitud |
|||||||
3 a 3.9 |
4 a 4.9 |
5 a 5.9 |
6 a 6.9 |
7 a 7.9 |
8 a 8.9 |
||
Profundidad (km) |
0 a 32,9 |
17615 |
9854 |
1319 |
112 |
9 |
4 |
33 a 69,9 |
9027 |
5066 |
656 |
44 |
6 |
1 |
|
70 a 149,9 |
17861 |
5057 |
469 |
31 |
4 |
0 |
|
150 a 299,9 |
7701 |
3400 |
170 |
21 |
3 |
0 |
|
300 a 499,9 |
49 |
17 |
2 |
2 |
0 |
0 |
|
500 a 800 |
68 |
132 |
38 |
21 |
5 |
0 |
|
Fuente: Elaborado por los autores (2018)
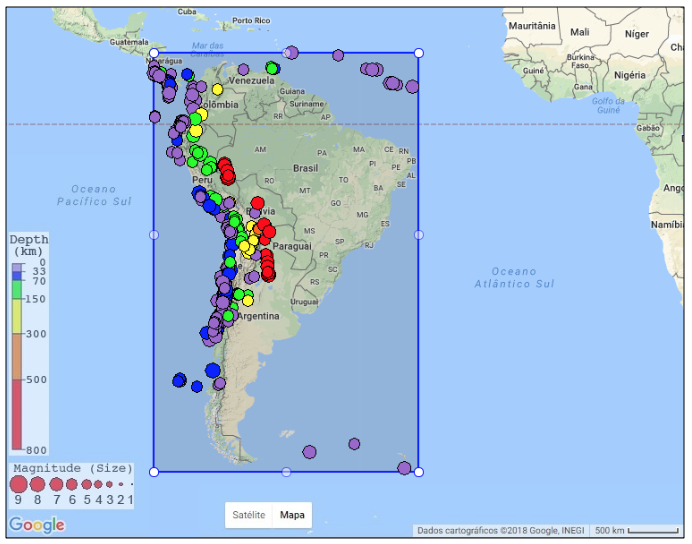
En la dirección electrónica del IRIS, es posible observar en el mapa las ocurrencias de los terremotos, como muestra la Figura 2. Este mapa presenta la región seleccionada para este estudio y terremotos con magnitud de 6 a 10, para todos los datos históricos.
Figura 2
Mapa con marcas de terremotos con una magnitud de 6 a 10
Fuente: Adaptado de la dirección electrónica del IRIS (2018)
Para poder calcular las matrices de transición, fue necesario definir intervalos para las magnitudes, como se muestra en el Cuadro 6.
Cuadro 6
Clasificación de los intervalos de magnitud
Clasificación |
Intervalo da magnitud |
3 |
3 a 3.9 |
4 |
4 a 4.9 |
5 |
5 a 5.9 |
6 |
6 a 6.9 |
7 |
7 a 7.9 |
8 |
8 a 8.9 |
Fuente: Elaborado por los autores (2018)
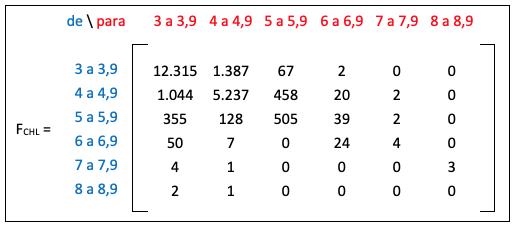
Con el intervalo de variaciones, fue posible analizar las frecuencias de terremoto en cada país, que ocurrieron variaciones en cada uno de estos intervalos, mostrados en la Figura 3 para Chile, 4 para Argentina, 5 para Colombia, 6 para los datos relacionados con la frontera entre Chile y Argentina, y 7 para los datos de Perú.
Figura 3
Matriz de frecuencia para Chile
Fuente: Elaborado por los autores (2018)
----
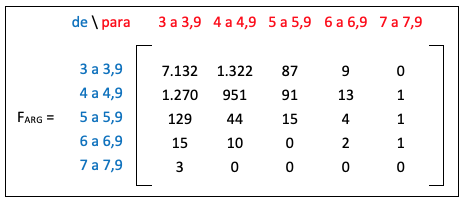
Figura 4
Matriz de frecuencia para Argentina
Fuente: Elaborado por los autores (2018)
----
Figura 5
Matriz de frecuencia para Colombia

Fuente: Elaborado por los autores (2018)
----
Figura 6
Matriz de frecuencia para frontera Chile-Argentina
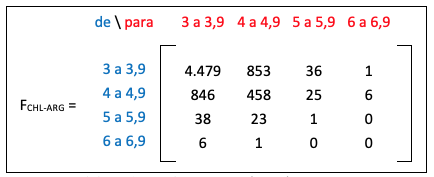
Fuente: Elaborado por los autores (2018)
----
Figura 7
Matriz de frecuencia para Perú
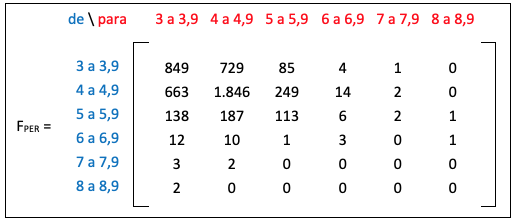
Fuente: Elaborado por los autores (2018)
Utilizando esta información, fue posible calcular la matriz con las probabilidades de transición de Markov, analizando cuántas veces varió del estado al estado . Las matrices se presentan en las Figuras 8 a 12, para Chile, Argentina, Colombia, frontera entre Chile y Argentina, y Perú, respectivamente.
Figura 8
Matriz de transición para Chile

Fuente: Elaborado por los autores (2018)
-----
Figura 9
Matriz de transición para Argentina
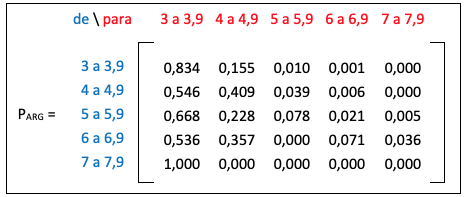
Fuente: Elaborado por los autores (2018)
-----
Figura 10
Matriz de transición para Colombia

Fuente: Elaborado por los autores (2018)
-----
Figura 11
Matriz de transición para frontera Chile-Argentina
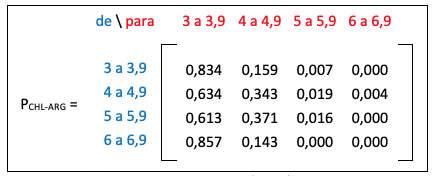
Fuente: Elaborado por los autores (2018)
-----
Figura 12
Matriz de transición para Perú

Fuente: Elaborado por los autores (2018)

Cuadro 7
Probabilidad de los estados
Intervalo de magnitud |
Probabilidad de estado |
||||
Chile |
Argentina |
Colombia |
Frontera CHL-ARG |
Perú |
|
3 a 3,9 |
63,67% |
77,01% |
82,45% |
79,27% |
33,86% |
4 a 4,9 |
31,15% |
20,97% |
16,30% |
19,7% |
56,35% |
5 a 5,9 |
4,74% |
1,74% |
1,15% |
0,92% |
9,10% |
6 a 6,9 |
0,39% |
0,25% |
0,06% |
0,10% |
0,55% |
7 a 7,9 |
0,04% |
0,03% |
0,04% |
– |
0,10% |
8 a 8,9 |
0,01% |
– |
– |
– |
0,04% |
Fuente: Elaborado por los autores (2018)
Con el Cuadro 7, se puede observar que hay una mayor probabilidad de estado estable del intervalo de 3 a 3,9 de magnitud para todas las localidades estudiadas, con la excepción de Perú, que la mayor probabilidad es del intervalo de 4 a 4,9 de magnitud. Además, calculando con la Ecuación 6 previamente presentada, es posible analizar el tiempo de repetición esperado para cada probabilidad de estado estable, conforme el Cuadro 8.
Cuadro 8
Tiempo de repetición esperado
Estado estable |
Tiempo de repetición esperado |
||||
Chile |
Argentina |
Colombia |
Frontera CHL-ARG |
Perú |
|
|
1,6 eventos |
1,3 eventos |
1,2 eventos |
1,3 eventos |
3,0 eventos |
|
3,2 eventos |
4,8 eventos |
6,1 eventos |
5,1 eventos |
1,8 eventos |
|
21,1 eventos |
57,5 eventos |
86,9 eventos |
109,2 eventos |
11,0 eventos |
|
256,1 eventos |
396,3 eventos |
1716,3 eventos |
967,6 eventos |
182,2 eventos |
|
2723,2 eventos |
3698,7 eventos |
2288,3 eventos |
– |
983,7 eventos |
|
7258,8 eventos |
– |
– |
– |
2457,9 eventos |
Fuente: Elaborado por los autores (2018)
Por medio del Cuadro 8, es posible visualizar que el tiempo de recurrencia de terremoto con intervalo de magnitud entre 3 a 3,9, por ejemplo, es de 1,6 eventos en Chile, es decir, se espera que después de 1,6 terremoto, ocurra otro de magnitud entre 3 y 3,9. En relación a terremotos con magnitud en el intervalo de 8 a 8,9 en Chile, después de ocurrir uno en esta franja, se prevé que otro del mismo intervalo de magnitud ocurrirá después de 7258,8 terremotos en Chile, independiente de las magnitudes.
Se ha estudiado la probabilidad de que se produzca un terremoto, dependiendo de la magnitud de los dos últimos eventos. Para ello, se realizó una nueva clasificación de las magnitudes, conforme Cuadro 9.
Cuadro 9
Clasificación de los intervalos de magnitud
Clasificación |
Intervalo de magnitud |
A |
3 a 4,9 |
B |
5 a 6,9 |
C |
7 a 8,9 |
Fuente: Elaborado por los autores (2018)
Para este análisis, hay 27 posibles combinaciones, por ejemplo, AA-A, o sea, ocurrieron dos terremotos con magnitudes entre 3 a 4,9 y se calcula la probabilidad de que el siguiente también esté dentro de esta banda. Todas las posibles combinaciones se presentan en el cuadro 10.
Cuadro 10
Posibles combinaciones de eventos
AA-A |
BA-A |
CA-A |
AB-A |
BB-A |
CB-A |
AC-A |
BC-A |
CC-A |
AA-B |
BA-B |
CA-B |
AB-B |
BB-B |
CB-B |
AC-B |
BC-B |
CC-B |
AA-C |
BA-C |
CA-C |
AB-C |
BB-C |
CB-C |
AC-C |
BC-C |
CC-C |
Fuente: Elaborado por los autores (2018)
Este análisis fue realizado individualmente para cada país estudiado. Los resultados se muestran en los Cuadros 11 a 15, para Chile, Argentina, Colombia, frontera entre Chile y Argentina, y Perú, respectivamente.
Cuadro 11
Análisis de 3 eventos para Chile
|
A |
B |
C |
AA |
97,37% |
2,62% |
0,01% |
AB |
79,59% |
20,41% |
0% |
AC |
100% |
0% |
0% |
BA |
98,03% |
1,97% |
0% |
BB |
26,47% |
72,45% |
1,08% |
BC |
57,14% |
42,86% |
0% |
CA |
100% |
0% |
0% |
CC |
100% |
0% |
0% |
Fuente: Elaborado por los autores (2018)
-----
Cuadro 12
Análisis de 3 eventos para Argentina
|
A |
B |
C |
AA |
98,17% |
1,82% |
0,01% |
AB |
89,50% |
9,50% |
1,00% |
AC |
100% |
0% |
0% |
BA |
96,97% |
3,03% |
0% |
BB |
90,48% |
9,52% |
0% |
BC |
100% |
0% |
0% |
CA |
100% |
0% |
0% |
Fuente: Elaborado por los autores (2018)
-----
Cuadro 13
Análisis de 3 eventos para Colombia
|
A |
B |
C |
AA |
98,79% |
1,17% |
0,04% |
AB |
96,25% |
3,75% |
0% |
AC |
100% |
0% |
0% |
BA |
97,50% |
2,50% |
0% |
BB |
100% |
0% |
0% |
CA |
100% |
0% |
0% |
Fuente: Elaborado por los autores (2018)
-----
Cuadro 14
Análisis de 3 eventos para frontera CHL-ARG
|
A |
B |
C |
AA |
98,98% |
1,02% |
0% |
AB |
98,53% |
1,47% |
0% |
BA |
100% |
0% |
0% |
BB |
100% |
0% |
0% |
Fuente: Elaborado por los autores (2018)
-----
Cuadro 15
Análisis de 3 eventos para Perú
|
A |
B |
C |
AA |
91,85% |
8,10% |
0,05% |
AB |
85,19% |
14,53% |
0,28% |
AC |
100% |
0% |
0% |
BA |
93,66% |
6,05% |
0,29% |
BB |
39,02% |
58,54% |
2,44% |
BC |
100% |
0% |
0% |
CA |
100% |
0% |
0% |
Fuente: Elaborado por los autores (2018)
Para Chile, después de dos terremotos de magnitud entre 3 y 4,9, hay una probabilidad de 97,37% de que el tercero también esté en esta franja. Para Argentina, después de una combinación AC, es decir, un evento de magnitud entre 3 y 4,9 seguido por otro de magnitud entre 7 y 8,9, hay una probabilidad del 100% de ocurrir un terremoto de magnitud entre 3 y 3, 4,9, esto se debe a que no se han producido combinaciones AC-B y AC-C entre enero de 2000 a abril de 2018.
Al analizar el cuadro de los resultados de Colombia, nunca hubo, dentro del período analizado en este trabajo, un terremoto de magnitud entre 5 a 6,9 seguido de otro de 7 a 8,9, por lo que la combinación BC no está en el Cuadro 13, así como las combinaciones CB y CC. Para la frontera entre Chile y Argentina, después de un evento de magnitud entre 3 y 4,9, seguido de otro de 5 a 6,9, hay un 98,53% de probabilidad de que el tercer ser de magnitud entre 3 y 4, 9, mientras que hay una probabilidad de 1,47% de ser de magnitud 5 a 6,9. Observando los datos del Perú, se percibe que hay una mayor probabilidad de que el tercer terremoto sea de magnitud 3 a 4,9 para todas las situaciones que ya ocurrieron en los años estudiados en este artículo, con la excepción de la combinación BB, o sea, dos eventos seguidos de magnitudes entre 5 y 6,9, en que la mayor probabilidad es de un tercero también en esta franja, con un 58,54% de probabilidad.
Este estudio aplicó Cadenas de Markov en el análisis de terremotos en América del Sur, utilizando una base histórica de datos de casi dos décadas. Debido a la seriedad que es este desastre natural, pudiendo ocasionar graves daños, es importante tener informaciones que puedan evaluar las probabilidades de un nuevo terremoto.
En la mayoría de los casos, se observó que la mayoría de las personas que se encontraban en la zona de estudio, Colombia y la frontera entre Chile y Argentina; sólo para Perú que la mayor frecuencia corresponde a la ocurrencia de un terremoto de magnitud entre 4 a 4,9 para otro de la misma franja, contando con 1846 eventos. Entonces, se calculó la matriz de transición para las cinco localidades, y las mayores probabilidades de transición del estado a la son para cuando j representa el intervalo de 3 a 3,9 de magnitud.
Dando continuidad en el estudio de las Cadenas de Markov, se calcularon las probabilidades de estado y tiempos de recurrencia. Para las cuatro primeras localidades, la mayor probabilidad de estado es referente a la primera banda de magnitud analizada; ya para Perú, es la segunda franja, debido a la mayor frecuencia de terremotos de magnitud entre 4 a 4,9. Este análisis de los resultados se repite para el tiempo de recurrencia, siendo el menor tiempo de 1,2 eventos para el estado estable en Colombia, y el mayor de 7259 eventos para el estado estable en Chile. Se realizó un análisis referente a tres eventos, es decir, se calculó la probabilidad de un tercer terremoto dependiendo de los dos anteriores.
De esta forma, fue posible y viable la utilización de cadenas de Markov para predecir la probabilidad de nuevos terremotos en América del Sur. Este artículo alcanzó sus objetivos satisfactoriamente, proporcionando resultados que pueden ser estudiados analíticamente.
ANDERSEN, Anders R; NIELSEN, Bo F; REINHARDT, Line B. Optimization of hospital ward resources with patient relocation using Markov chain modeling. European Journal of Operational Research. Vol 260, Año 2017, Número 3, Pág. 1152-1163. Recuperado de: https://www.sciencedirect.com/science/article/abs/pii/S0377221717300619
ASIM, Khawaja; IDRIS, Adnan; IQBAL, Talat; MARTÍNEZ-ÁLVAREZ, Francisco. Seismic indicators based earthquake predictor system using Genetic Programming and AdaBoost classification. Soil Dynamics and Earthquake Engineering. Vol 111, Año 2018, Pág. 1-7. Recuperado de: https://www.sciencedirect.com/science/article/pii/S0267726118301349
DEPARTAMENTO DEL INTERIOR DE EEUU. Investigación Geológica. La gravedad de un terremoto. Año 1997, Pág. 421-530. Recuperado de: https://pubs.usgs.gov/unnumbered/70039541/report.pdf
HILLIER, Frederick; LIEBERMAN, Gerald. Introduction to Operations Research. 8. ed. Nova Iorque: McGraw-Hill, 2005.
HUNTER, Jeffrey. The computation of the mean first passage times for Markov chains. Linear Algebra and its Applications. Vol 549, Año 2018, Pág. 100-122. Recuperado de: https://arxiv.org/abs/1701.07781
Incorporated Research Institutions for Seismology – IRIS. Sitio institucional. Recuperado de: <http://www.iris.edu/hq/
ROSHAN, Gholamreza; NASTOS, Panagiotis T. Assessment of extreme heat stress probabilities in Iran's urban settlements, using first order Markov chain model. Sustainable Cities and Society. Vol 36, Año 2018, Pág. 302-310. Recuperado de: https://www.sciencedirect.com/science/article/pii/S2210670717308168
STAUDT, Francielly H; COELHO, Antonio S; GONÇALVES, Mirian B. Determinação da capacidade real necessária de um processo produtivo utilizando cadeia de Markov. Production. Vol 21, Año 2011, Número 4, Pág. 634-644. Recuperado de: http://www.scielo.br/pdf/prod/v21n4/aop_t6_0005_0238.pdf
TAHA, Hamdy. Operations Research: an introduction. 8. ed. New Jersey: Pearson Prentice Hall, 2007.
YANG, Hongxing; LI, Yutong; LU, Lin; QI, Ronghui. First order multivariate Markov chain model for generating annual weather data for Hong Kong. Energy and Buildings. Vol 43, Año 2011, Número 9, Pág. 2371-2377. Recuperado de: https://www.sciencedirect.com/science/article/pii/S0378778811002556
1. Maestro en Ingeniería Mecánica. Correo electrónico de contacto: rafaelacechin@hotmail.com
2. Doctor en Ingeniería Mecánica en el Área del Conocimiento de Ciencias Exactas e Ingenierías de la Universidad de Caxias do Sul. Correo electrónico de contacto: Leandro.lcorso@gmail.com