

Vol. 40 (Nº 01) Año 2019. Pág. 18
CASTRO, Yamile 1; HUERTAS, César A. 2; OBANDO, Carlos E. 3; VALENCIA, Carlos F. 4
Recibido: 26/07/2018 • Aprobado: 14/11/2018 • Publicado 14/01/2019
RESUMEN: En este estudio se desarrolla un modelo de análisis de supervivencia para analizar el comportamiento de las empresas del sector de comercio minorista (retail) en Colombia. El objetivo es predecir la probabilidad de riesgo de quiebra en función del tiempo a partir de razones financieras, por medio de metodologías interpretables como los modelos aditivos generalizados GAM y la regresión de Cox. Adicionalmente, se desarrolla un mecanismo de selección de variables y métricas evaluación de desempeño mediante validación cruzada. |
ABSTRACT: . In this study we develop a survival analysis model for the analysis of the behavior of firms in the retail sector of Colombia. The main purpose is to predict the bankruptcy probability as a function of time and incorporating the information of financial ratios. We use interpretable methodologies as the generalized additive model and the Cox regression. In addition, we propose a novel variable selection mechanism and adequate metrics for performance measuring using cross-validation. |
La bancarrota se define como el resultado de una condición crónica en la que el total de pasivos de una firma excede el valor de sus activos. Dicha situación de insolvencia permanente puede estar asociada a manejos administrativos incorrectos, efectos en la economía, transformaciones coyunturales del mercado, problemas de liquidez, entre otros factores que afectan directamente los resultados financieros de la compañía. La insolvencia generalizada puede causar efectos colaterales al resto del sistema financiero y provocar una crisis sistémica, razón por la cual se establece el Acuerdo de Basilea II (2004), con el fin de crear un estándar internacional que le permita a los reguladores bancarios establecer requerimientos de capital necesarios frente a los riesgos financieros y operativos en los que pueden incurrir las compañías, es decir, creación de portafolios crediticios de acuerdo al incumplimiento de los clientes. A partir de lo anterior, conocer de antemano cuando una firma va a entrar en bancarrota es una información valiosa que impacta muchas decisiones en el sistema financiero y de allí se deriva la importancia del desarrollo de herramientas analíticas que permitan determinar los factores económicos relevantes para predecir el estrés financiero.
Una de las metodologías más trabajadas a través del tiempo para la explicación de la bancarrota corresponde al uso de razones financieras (Bellovary, Giacomino, & Akers, 2007). Se trata de estudiar las relaciones de variables del estado económico de una compañía, categorizadas en razones de liquidez las cuales miden el dinero en efectivo para el pago de deudas, de actividad o eficiencia que permiten identificar la rapidez de convertir los activos no-corrientes en activos corrientes, razones de deuda con las que se puede medir el pago de deudas de largo plazo, de ganancia las cuales evalúan los activos y el control de los gastos, y por último razones de mercado que relacionan el rendimiento y el valor de una inversión en acciones de la compañía.
El estudio para determinar el estrés financiero a través del uso de razones financierasy métodos estadísticos inicia en 1932 cuando Fitzpatrick da origen a la etapa descriptiva y posteriormente en 1968 Altman inicia la etapa predictiva con el desarrollo de modelos multivariados (Altman, 1968). Las siguientes metodologías se basaron en técnicas estadísticas clásicas de clasificación, a partir de las cuales es posible tener una interpretación sencilla de los resultados, tales como análisis discriminante lineal, regresión logística y modelos probit. Durante los últimos años, se han realizado numerosos estudios de nuevas metodologías para la predicción de quiebra basadas en aprendizaje automático e inteligencia artificial como son: redes neuronales artificiales (Atiya, 2001; Wilson & Sharda, 1994), máquinas de soporte vectorial (Shin, Lee, & Kim, 2005; Lin, Yeh, & Lee, 2011) y métodos de ensamble (Wang & Ma, 2012; Kim & Kang, 2010). En general, estas últimas metodologías ofrecen un mejor rendimiento de clasificación que los modelos estadísticos paramétricos clásicos; sin embargo, aunque los algoritmos predictivos de caja negra funcionan muy bien para predecir cuándo se producirá la bancarrota, no dan razón por la cual sucede. De esta forma, un buen modelo de predicción de bancarrota debe considerar desempeño, precisión e interpretabilidad, a partir del cual sea posible describir el comportamiento estático y dinámico de los indicadores financieros.
En Colombia, se establece la existencia de dos tipos de liquidación para las sociedades, liquidación voluntaria y liquidación judicial; la primera hace referencia a la disolución de una compañía por ocurrencia de unas de las causales previstas en los estatutos o en la ley y la segunda es un proceso consagrado en la Ley 1116 de 2006, por medio de la cual se establece el Régimen de Insolvencia Empresarial, el cual persigue la liquidación pronta y ordenada, buscando el aprovechamiento del patrimonio del deudor. Dentro de los estudios que se han realizado, se destacan el de Gomez-Gonzalez & Kiefer (2006) enfocado en entender los factores que determinaron el estrés financiero de las instituciones bancarias a finales de 1990 y principios del año 2000. Como resultado del estudio se evidenció que este fenómeno en gran medida se dio gracias a una fuerte caída en la razón financiera de capitalización de las empresas, en conjunto con la rentabilidad y liquidez. Por otro lado, Gómez, Hinojosa, & Zamudio (2006) proponen un análisis de la probabilidad condicional de incumplimiento de los mayores deudores privados del sistema financiero colombiano utilizando las variables del modelo Camel. El principal hallazgo del estudio revela que el nivel de la deuda de las empresas es el principal determinante de la probabilidad condicional de incumplimiento con un efecto adicional que aporta pertenecer a ciertos sectores económicos como la construcción.
Más recientemente, Carlos Valencia et al. (2014), desarrollaron un nuevo enfoque al usar un modelo generalizado aditivo para la predicción de bancarrota con un mecanismo integrado para la selección de variables. Tomando como referencia esta nueva perspectiva, surge la idea de explorar un modelo interpretable y eficiente con la metodología de análisis de supervivencia junto con un modelo aditivo generalizado (GAM) estimado a través de la selección de variables. Cuando el efecto encontrado es una función lineal, se obtiene un solo parámetro que representa la contribución marginal a las razones de momios (odds ratios); en el caso no lineal, se obtiene una función que puede ser interpretable debido a la propiedad aditiva (Berg, 2006). Además, la selección de variables producirá una estimación en la que se descartan predictores no significativos para la explicación de la bancarrota.
El objetivo de utilizar modelos de supervivencia para la predicción de la bancarrota es obtener, además de la clasificación del riesgo, la probabilidad de que ocurra la insolvencia dado una ventana de tiempo. El periodo de supervivencia se define como el tiempo transcurrido desde el estado inicial, año 2007, hasta el estado final (10 años). Para el estudio, se habla de datos censurados a la derecha, ya que después del tiempo de estudio, no se conoce el estado de las sociedades que no quebraron durante el análisis.
De acuerdo con todo lo mencionado previamente y dada la importancia de la insolvencia financiera frente a los efectos adversos en la economía del país, el propósito de este proyecto es estimar un modelo de análisis de supervivencia que permita analizar el comportamiento de las empresas de comercio minorista colombianas y predecir la probabilidad de riesgo de quiebra en función del tiempo a partir de razones financieras usadas como variables explicativas. Se presenta la aplicación de este tipo de análisis, desde la identificación de información requerida, diversas fuentes, minería de datos, análisis y consolidación hasta el ajuste, calibración y evaluación de un modelo lineal y no lineal. A continuación se explica la metodología desarrollada en el trabajo, en la cual se incluye la descripción de los métodos, información e indicadores analizados; enseguida se presenta la sección de resultados obtenidos durante el proceso de estimación y finalmente las conclusiones y recomendaciones.
La función de supervivencia se define como la probabilidad que un individuo sobreviva al momento , que en este estudio equivale a la probabilidad que una sociedad no se declare en bancarrota al tiempo . La variable aleatoria positiva representa el tiempo hasta el evento de interés de un individuo y la función de supervivencia se puede formular como:

En el presente estudio, es de interés determinar la influencia de las covariables sobre el tiempo de supervivencia de las compañías, razón por la que se desea realizar las estimaciones usando el modelo de Cox. Este modelo propuesto por primera vez por Cox (1972), es llamado modelo de riesgos proporcionales, debido a que el cociente entre el riesgo para dos empresas es constante en el tiempo. El Modelo Cox consiste en expresar la función de riesgo en dos componentes, uno no paramétrico que depende sólo del tiempo y otro paramétrico que depende sólo de las variables, de la siguiente forma:

En el modelo GAM los predictores son funciones suaves desconocidas estimadas a partir de la distribución de las variables de entrada. Este modelo fue desarrollado para mezclar propiedades de modelos lineales generalizados con modelos no-paramétricos.

En este caso, se utilizó la función GAM del paquete MGCV en R que realiza el ajuste del parámetro de suavización mediante la función magic (Wood, S.N., 2004), en la cualinternamente aplica método de Newton de manera multi-dimensional en combinación con validación cruzada sobre la población de entrenamiento para hallar el factor de suavización óptimo.
Como ventajas del modelo se tiene que produce formas flexibles y sin importar la dimensionalidad, además es eficiente computacionalmente y es fácil de interpretar cada función separadamente, sin embargo, la forma funcional está limitada a ser aditiva.
La selección de variables es el proceso de escoger predictores significativos para la construcción de modelos. Generalmente, entre más variables sean incluidas en un modelo, el ajuste a los datos mejora pero aumenta el número de parámetros a estimar y disminuye la precisión al incrementarse la varianza produciendo un sobreajuste. Por el contrario, si se incluyen menos variables de las necesarias, la volatilidad se reduce pero aumenta el sesgo y por tal razón se tendrá una mala predicción. Por otra parte, algunos predictores pueden afectar la confiabilidad del modelo, principalmente si están correlacionados con otros.
Debido a lo anterior, la motivación para hacer selección de variables es encontrar un modelo que busque un equilibrio entre bondad de ajuste y parsimonia, mejore interpretabilidad, reduzca el tiempo de entrenamiento, evite el problema de la dimensionalidad y disminuya el sobreajuste.
Se utilizó la selección exhaustiva de variables, en la cual se busca el mejor modelo entre todas las combinaciones posibles de variables, para un conjunto de p variables se realiza la calibración y evaluación de 2p posibles subconjuntos. Es importante resaltar que esta técnica demanda una alta capacidad computacional y tiempo de ejecución extenso debido a la cantidad de modelos que son calculados y evaluados. Para seleccionar el modelo, se establece una medida global de evaluación que tenga en cuenta el ajuste y se escogerá el modelo cuya medida global sea la mejor.
El criterio usado para la evaluación de los modelos fue el AUC, que representa el área bajo la Curva ROC cuya finalidad es analizar todos los valores para la relación entre sensibilidad y especificidad en función del umbral. Por lo anterior se presenta una descripción de la metodología para mayor entendimiento.
La sensibilidad es la probabilidad de clasificar correctamente una compañía en bancarrota cuando ésta presenta insolvencia, (TPF – Fracción de verdaderos positivos) y la especificidad es la probabilidad de catalogar una sociedad solvente cuando la empresa presenta estados financieros controlados (TNF- Fracción de verdaderos negativos). Los valores continuos pueden ser transformados en binarios si se establece un punto de corte (- Umbral) a partir del cual se considerarán los resultados como quiebra o no quiebra. Sea la variable binaria que denota el estado verdadero de solvencia y el resultado binario del pronóstico, entonces, los resultados del modelo pueden ser:

La Curva ROC permite describir que tan separadas están las distribuciones de la sensibilidad y la especificidad de una muestra de validación, definido como y dado que la curva ROC es una función monótona creciente en el primer cuadrante entonces , donde la función ROC es aquella a la que cada valor de le hace corresponder , siendo un punto de corte particular, para el cual . El Área Bajo la Curva ROC (Area Under the Curve, AUC) estima la capacidad que tiene un modelo de discriminar entre bancarrota y no bancarrota; definido por y por tanto, a mayor área bajo la curva el modelo producirá un mejor ajuste.
Ahora se detallarán las anteriores definiciones para datos de supervivencia y para esto se presenta cómo influye el tiempo en las variables definidas anteriormente. En el análisis de supervivencia se define como la variable tiempo hasta la ocurrencia de la quiebra para la compañía , por tanto se crea una nueva variable binaria que representa el estado de la solvencia de la empresa en el tiempo . Heagerty & Zheng (2005) proponen las siguientes definiciones de casos y controles dependientes del tiempo y su clasificación:
Casos: Individuos que presentan el fallo. Utilizados para definir la sensibilidad.
Controles: Individuos que no presentan el fallo. Utilizados para definir la especificidad.
Dado lo anterior, las extensiones de la definición de la curva ROC para eventos dependientes del tiempo surgen por la elección de un tipo de casos (incidentes o acumulativos) y un tipo de controles (estáticos o dinámicos), dando lugar a tres posibles exposiciones de la curva ROC:
De acuerdo con lo anterior, es fundamental tener en cuenta que
Para la evaluación de los modelos de este estudio el criterio que se utilizó fue el AUC y dado que la característica de la curva de ROC es Incidente-Dinámico, entonces es posible promediar los AUC en el tiempo. Por tanto el mejor modelo seleccionado es aquel con mayor promedio de AUC en la ventana de tiempo definida.
La evaluación de desempeño sobre los modelos predictivos ya calibrados se realizó mediante validación cruzada, técnica que se usa en el aprendizaje automático para evaluar tanto la variabilidad de un conjunto de datos como la confiabilidad del modelo entrenado.
La validación cruzada divide aleatoriamente los datos en varias particiones y cada una ellas es fraccionada en conjunto de datos de entrenamiento y validación; para cada muestra de entrenamiento se crea un modelo que luego es probado en la muestra de validación. Cuando el proceso de construcción y evaluación se completa para todos las muestras, se genera un conjunto de medidas de rendimiento (AUC) y resultados para todos los datos.
Al comparar las estadísticas para todas las particiones se puede evaluar la confiabilidad y precisión de las predicciones, además de interpretar la calidad del conjunto de datos y comprender si el modelo es susceptible a variaciones en la información.
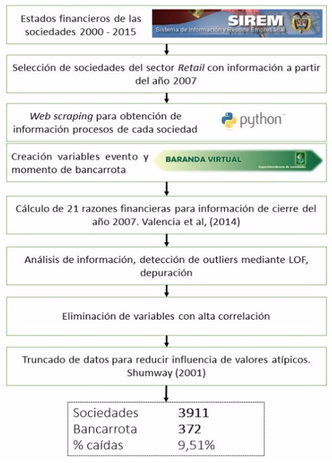
La muestra de estudio fue tomada a partir de la información reportada para consulta pública por las sociedades sujetas a vigilancia y control por parte de la Superintendencia de Sociedades. A través del sistema de Información y Reporte Empresarial - SIREM – fue posible consultar los Estados Financieros anuales reportados por las compañías bajo estudio. Se obtuvieron todos los estados financieros reportados desde el año 2000 hasta el año 2015 y se consolidaron las sociedades que reportaron información, encontrando en total 48,600 sociedades con al menos el reporte de un estado financiero en el horizonte de tiempo analizado. Con base en la Clasificación Industrial Internacional Uniforme (código CIIU) se definieron 45 tipos de actividades asociadas al sector retail.
Una de las mayores dificultades en el desarrollo de este tipo de estudios es la obtención de la variable que describe el momento en el cual se considera que una sociedad entra en bancarrota, debido a que esta información no se encuentra explicita en los estados financieros o reportes realizados por las sociedades.
Para dar solución a este problema, se realizó una revisión de los sistemas de reporte existentes en las entidades que regulan y vigilan las sociedades (Superintendencias, Cámaras de comercio, dirección de impuestos), de esta forma se identificó el sistema público de información Baranda Virtual, de la Superintendencia de Sociedades, el cual permite obtener información acerca de cambios de estado, procesos, avisos, autos y resoluciones puntuales de cada sociedad. A partir del entendimiento del proceso de liquidación de las sociedades, se identificaron los criterios de reorganización, liquidación u otro asociado al cese de actividades. Con base en esto, se estableció el criterio de bancarrota a partir de las fechas de cambios de estado y procesos asociados a liquidación o reorganización.
La consulta de información en Baranda Virtual se debía realizar puntualmente a través de un formulario de búsqueda por número de NIT, teniendo en cuenta la cantidad de sociedades a consultar se requirió un desarrollo adicional para obtener masivamente la información. Para esto se implementó un proceso de web scraping en lenguaje de programación Python, con el cual se accedió de forma automática y remota a la aplicación y se obtuvo toda la información acerca de la sociedad, etapas y causas de su estado actual, así como las fechas relevantes (constitución, estado, etapa, situación). A partir de dicha información, fue posible generar la variable respuesta asociada al evento de bancarrota y el momento del tiempo en que sucedió.
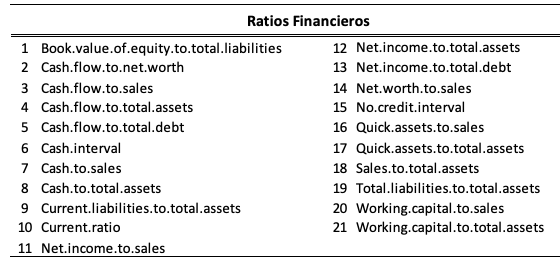
El estudio se centró en analizar las sociedades que reportaron información en el año 2007, con el fin de tener una ventana de tiempo de 10 años en los cuales, el número de empresas en estado de bancarrota fuera significativo. Así las cosas, el panel final de datos, antes del análisis exploratorio quedó constituido por 4048 sociedades del sector minorista. Para la definición y cálculo de las razones financieras utilizadas como predictores, se tomaron en cuenta los 21 indicadores [5] propuestos por Valencia et al, (2014), detallados en la Tabla 1.
Tabla 1
Razones financieras, consideradas como predictores
Una vez calculadas las razones, se realizó un análisis descriptivo de la información y detección de valores atípicos mediante el algoritmo LOF (Breunig et al (2000)), de acuerdo con esto, se excluyeron 137 sociedades. Uno de los principales enfoques de este trabajo ha sido garantizar la calidad de la información, centrándose en entender desde el origen de los datos posibles errores u omisiones en lo que se reporta a la entidad reguladora. A partir de esto, y con base en los resultados obtenidos en el presente estudio, retirar de la base de datos aquellos registros cuya información de ingresos operacionales sean cero o uno en lugar de imputarlos permitirá capturar el comportamiento real de la base de datos, ya que, de tomar la segunda opción se estaría realizando suposiciones fuertes sobre las ventas realizadas por las empresas en el año de reporte y con la cual se estiman aproximadamente nueve razones financieras utilizadas dentro del análisis.
Se eliminaron variables que presentan correlaciones superiores a 0.8, criterio sugerido por Gujarati (1988) (Partington & Kim, 2008), tales como capital de trabajo sobre activos totales (working capital to total assets), deudas totales sobre activos totales (total liabilities to total assets), ingreso neto sobre ventas (net income to sales). Por último, siguiendo el enfoque de Shumway (2001) para reducir la influencia de los valores atípicos, se realizó un truncado de los datos en cada variable para los valores inferiores al primer percentil y superiores al percentil 99.
La muestra final es de 3911 sociedades de las cuales 372 (9,51%) presentaron bancarrota en la ventana de tiempo de 10 años. La Tabla 2 presenta las sociedades que cayeron en insolvencia año a año durante la ventana de estudio. En la Ilustración 1, se presenta un resumen de todo el proceso de minería de datos, análisis y depuración que se realizó.
Tabla 2
Clasificación de estado de sociedades en la ventana de estudio.
Año |
2008 |
2009 |
2010 |
2011 |
2012 |
2013 |
2014 |
2015 |
2016 |
2017 |
Total |
Censura |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
3539 |
3539 |
Bancarrota |
20 |
35 |
53 |
38 |
44 |
56 |
55 |
35 |
23 |
13 |
372 |
Ilustración 1
Proceso minería de datos, análisis y depuración de la información
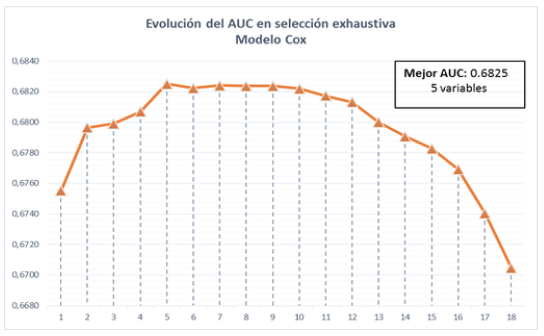
Para la selección del modelo de regresión de Cox, tal como se menciona en la sección 2, se aplicó la técnica de búsqueda exhaustiva para hallar la mejor combinación de variables posibles tomando como medida de desempeño el promedio de los AUC en la ventana de tiempo analizada. Mediante un proceso de validación cruzada (3-Fold Cross-Validation) se evaluaron 262.144 subconjuntos, resultados de la combinación de 18 variables. El tiempo de ejecución de todos los modelos fue de 15 horas de forma secuencial por una sola máquina [5].
Se seleccionó un modelo de cinco variables, el cual presentó el mejor desempeño promedio en las muestras de validación con un AUC = 0,6825. La Ilustración 2, presenta el comportamiento del mejor AUC de acuerdo con la cantidad de variables. Se puede observar cómo existe un punto máximo donde se obtiene el mejor AUC y a medida que se aumenta el número de predictores el desempeño empeora, esto se asocia con el sobreajuste.
Las variables seleccionadas, los coeficientes estimados y sus medidas de validación se presentan en la Tabla 3. En este caso, todas las variables son significativas al 5%. El modelo es aceptable para cualquiera de los tres criterios de test de razón de verosimilitud y prueba de Wald.
Se validó el ajuste del modelo de regresión de Cox con la hipótesis fundamental de que los riesgos son proporcionales, encontrando que no existen evidencias significativas al 5 % de que se viole este supuesto tanto globalmente como para las cinco variables seleccionadas.
Tabla 3
Modelo ajustado riesgos proporcionales Cox
Financial Ratio |
Β |
exp(β) |
se(β) |
z |
Pr(>|z|) |
Sig |
Current.liabilities.to.total.assets |
(1,053) |
0,349 |
0,531 |
-1,984 |
0,047 |
* |
Net.income.to.total.assets |
(14,840) |
0,000 |
1,941 |
-7,646 |
0,000 |
*** |
No.credit.interval |
(0,004) |
0,996 |
0,002 |
-2,331 |
0,020 |
* |
Quick.assets.to.sales |
0,681 |
1,977 |
0,305 |
2,234 |
0,026 |
* |
Quick.assets.to.total.assets |
1,345 |
3,836 |
0,532 |
2,527 |
0,012 |
* |
Likelihood ratio test= 94.53 on 5 df, p=0
Wald test = 79.48 on 5 df, p=1.11e-15
Score (logrank) test = 85.55 on 5 df, p=1.11e-16
Ilustración 2
Evolución del AUC en Modelo Cox
------
Ilustración 3
Gráfico de la función de supervivencia. Modelo CPH

Interpretando las salidas, se concluye que los ratios de liquidez (quick assets to total assets y quick assets to sales) aumentan la razón de riesgo a medida que su valor se incrementa, mientras que las razones de apalancamiento (current liabilities to total asset) y de rentabilidad (net income to total assets) reducen la razón de riesgo a medida que su valor aumenta.
La Tabla 4, presenta los coeficientes β y exp(β) de cada una de las variables en mención.
Tabla 4
Interpretación de variables significativas
Financial Ratio |
Tipo |
β |
exp(β) |
Current liabilities to total assets |
Apalancamiento |
(1,053) |
0,349 |
Net income to total assets |
Rentabilidad |
(14,840) |
0,000 |
No credit interval |
Liquidez |
(0,004) |
0,996 |
Quick assets to sales |
Liquidez |
0,681 |
1,977 |
Quick assets to total assets |
Liquidez |
1,345 |
3,836 |
De acuerdo con esto, se observa que bajo el resultado del modelo de regresión de Cox, para una empresa del sector retail una reducción en la liquidez aumenta la razón de riesgo de bancarrota, y un aumento de la rentabilidad, lo reduce. Lo cual es congruente con la dinámica del sector estudiado.
Al igual que para los modelos de Cox, se aplica el método de selección exhaustiva generando 262.144 combinaciones de variables diferentes para las cuales se realizó un ajuste con 3 fold Cross-Validation. Para la selección exhaustiva fue necesario ejecutar los modelos en varios equipos dado que el tiempo computacional es mucho mayor que con un modelo lineal, para esto se utilizaron ocho equipos para un periodo de ejecución de 1300 horas. La Ilustración 4, presenta el comportamiento del mejor AUC de acuerdo con la cantidad de variables.
Ilustración 4
Evolución del AUC en Modelo Gam
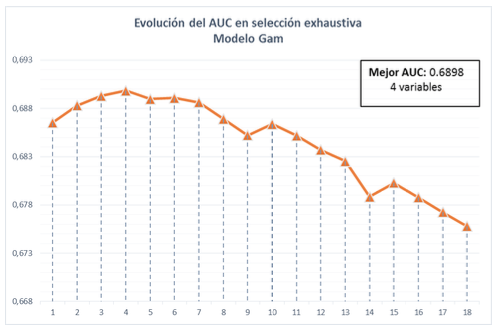
El modelo con mejor desempeño se encuentra dentro del grupo de cuatro variables con un AUC promedio de 0.689. La Tabla 5, presenta las variables significativas evaluadas a un nivel de significancia del 5%.
Tabla 5
Interpretación de variables significativas
Financial Ratio |
Edf |
Ref.df |
Chi.sq |
P-value |
Sig |
Cash interval |
1.004 |
1.009 |
2.185 |
0.1397 |
|
Net income to total assets |
3.150 |
3.863 |
128.110 |
<2e-16 |
*** |
Net worth to total sales |
1.994 |
2.444 |
11.137 |
0.0101 |
* |
Quick assets to sales |
2.162 |
2.658 |
9.997 |
0.0195 |
* |
En general se obtiene una curva de supervivencia (Ilustración 5) donde se puede inferir que para el sector de comercio minorista en Colombia con la información analizada, el riesgo de entrar en estado de liquidación es bajo (probabilidad inferior al 10%).
Ilustración 5
Curva supervivencia modelo GAM

Dentro de las variables incluidas en el modelo, el indicador Cash interval describe el nivel de efectivo del cual se dispone para cubrir los gastos de operación. Para este caso, dicha variable refleja un comportamiento lineal directo sobre el riesgo de bancarrotade una empresa (Ilustración 6).
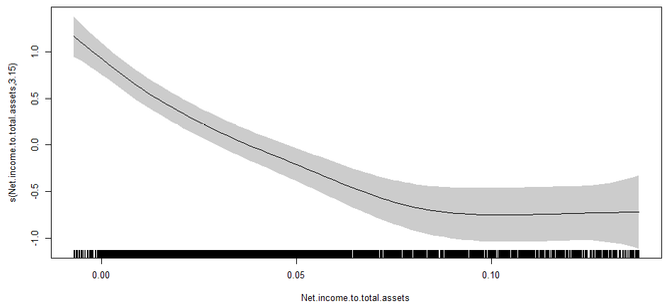
Al analizar la variable ingreso neto sobre total de activos (net income to total assets) se puede evidenciar que la relación es no lineal con respecto al estrés financiero. Esto permite tener una mayor claridad de su efecto dado que bajo el modelo de Cox, la intuición que se tenía era que mientras más alta la capacidad de generar ingresos por cada peso del activo (mayor rentabilidad), menor era el riesgo al que estaba expuesta la firma; sin embargo, como se puede observar en la Ilustración 7, hay un determinado punto (0.1), a partir del cual, el incremento en los niveles de rentabilidad de la empresa no implica una reducción total del riesgo de bancarrota.
Ilustración 6
Efecto de la variable Cash Interval sobre razón riesgo de bancarrota

-----
Ilustración 7
Efecto de la variable Net income to total assets
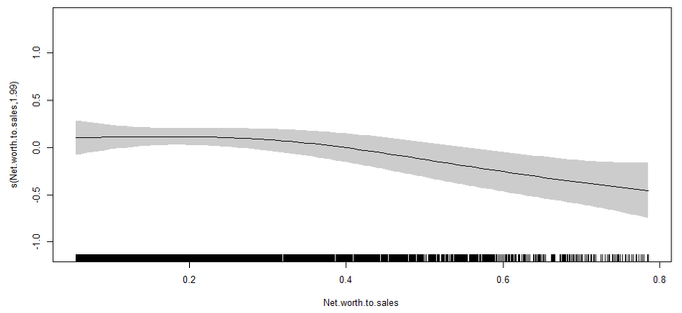
Para la variable Net worth to sales (ventas generadas con el patrimonio que se tiene), el efecto está compuesto por dos segmentos, uno constante para valores inferiores a 0.2 en el indicador, y otro que genera una disminución en la razón de riesgo una vez que se supera el valor mencionado. En términos financieros, se puede concluir que un alto valor en esta variable, implica que el nivel de ventas alcanzado es más que suficiente para respaldar sus obligaciones (Ilustración 8).
Ilustración 8
Efecto de la variable Net worth to sales
Finalmente, la variable Quick assets to sales refleja un comportamiento no lineal sobre el riesgo de quiebra para las compañías de retail en Colombia. Esto, desde el punto de vista de la información que captura la variable, indica que el porcentaje que representan los activos líquidos sobre las ventas tiene un impacto inverso sobre la razón de riesgo siempre y cuando sea inferior a 0.5. A partir de dicho punto, este indicador tendrá un impacto positivo sobre la probabilidad de bancarrota (Ilustración 9).
Ilustración 9
Efecto de la variable Quick assets to sales

La situación de insolvencia causa efectos colaterales en la sociedad, de ahí la importancia de desarrollar herramientas analíticas para predecir el estrés financiero y determinar los factores económicos relevantes. Las entidades reguladoras, encargadas de la vigilancia y control de las sociedades comerciales, deben incorporar en sus procesos de solicitud de información, toda aquella relacionada con estrés financiero y bancarrota. Facilitar el acceso a esta información al sector académico y técnico permitirá el desarrollo de estudios que conlleven al entendimiento y faciliten una mejor toma de decisiones por parte del ente gubernamental. En este proyecto se pretende aportar a la investigación económica colombiana, apoyado en la minería de datos y buscando extrapolar ejercicios académicos a información real del país, que luego pueden ser utilizados en la obtención de resultados más precisos de predicción y que permitan ser una herramienta de soporte en la toma de decisiones.
A diferencia de las aplicaciones clásicas para predicción de bancarrota donde se conoce para una ventana de tiempo fija e inamovible la estimación con base en unas variables independientes, el análisis de supervivencia, además de estimar una razón de riesgo en función del tiempo, permite a las entidades reguladoras generar alertas y ser proactiva en sus acciones de vigilancia y control orientadas a mitigar dicho riesgo en el corto, mediano o largo plazo según cada distribución. Esto derivará en mayor eficiencia en el esfuerzo que se realice y una mayor efectividad en el proceso de intervención.
En los estudios de supervivencia para predecir bancarrota existe la limitante de obtener el momento exacto en el que una compañía entra en estado de liquidación. Algunos trabajos presentan metodologías para inferir esta información a partir de la suspensión de reportes financieros de un año al siguiente; sin embargo, este proyecto presenta un aporte relevante al construir una metodología para identificar el momento en el que ocurre la bancarrota a través de la obtención de los estados financieros y el entendimiento de la información pública acerca del proceso de insolvencia, así como la identificación de características de liquidación no asociadas al desempeño económico tales como fusiones, liquidación voluntaria, entre otros.
Aunque la regresión de Cox es una metodología muy utilizada para analizar el efecto de las covariables, en el contexto financiero es importante tener precaución ya que este modelo está sujeto al cumplimiento de supuestos de riesgos proporcionales, covariables invariantes en el tiempo y relación lineal entre la función de riesgo y los predictores. En consecuencia, si el supuesto de riesgos proporcionales no se cumple, los resultados bajo el modelo de Cox no son los más adecuados; una alternativa es utilizar Modelos Aditivos Generalizados (GAM), que incorpora funciones no paramétricas que se adaptan a la estructura no lineal de los datos, manteniendo la interpretabilidad y mejorando el entendimiento del efecto de los predictores. Así mismo, el tratamiento o no de valores atípicos afecta significativamente el desempeño de los modelos lineales como la regresión de Cox. Caso contrario ocurre con los modelos GAM, que a partir de su capacidad de ajuste mediante la suavización de sus funciones, permiten capturar de una mejor manera el comportamiento de estos valores y reflejarlos en la función resultante.
Abogados Bogotá. (2015). Gestion compartida. Obtenido de: https://www.gestioncompartida.com/sitio/beneficios-y-requisitos-de-la-ley-1429-de-2010-actualizacion
Altman, E. I. (1968). Financial Ratios, Discriminant Analysis and the Prediction of Corporate Bankruptcy. American Finance Association, 589-609.
Argyropoulos, C., & Unruh, M. L. (2015). Analysis of Time to Event Outcomes in Randomized Controlled Trials by Generalized Additive Models. Albuquerque, New Mexico, United States of America: Department of Internal Medicine, Division of Nephrology, University of New Mexico.
Atiya, A. F. (2001). Bankruptcy Prediction for Credit Risk Using Neural Networks: A Survey and New Results. IEEE TRANSACTIONS ON NEURAL NETWORKS, 12(4), 929 - 935.
Beaver, W. H., McNichols, M. F., & Rhie, J.-w. (2005). Have Financial Statements Become Less Informative? Evidence from the Ability of Financial Ratios to Predict Bankruptcy. Review of Accounting Studies, 10, 93–122.
Bellovary, J. L., Giacomino, D., & Akers, M. D. (2007). A Review of Bankruptcy Prediction Studies 1930-Present. Journal of Financial Education, 33, 1-42.
Benavides, A. R. (2017). Curvas ROC (Receiver-Operating-Characteristic) y sus aplicaciones. Universidad de Sevilla. Sevilla: Departamento de Estadística e Investigación Operativa. Obtenido de http://hdl.handle.net/11441/63201
Chouldechova, A., & Hastie, T. (2015). Generalized additive model selection.
Gómez, J. E., Hinojosa, I. P., & Zamudio, N. E. (2006). Análisis de la probabilidad condicional de incumplimiento de los mayores deudores privados del sistema financiero colombiano. Temas de Estabilidad Financiera. Banco de la República.
Gómez-Gonzalez, J. E., & Kiefer, N. M. (2006). Explaining time to bank failure in Colombia. Borradores de economía. Estudios Económicos del Banco de la República.
Grice, J. S., & Dugan, M. T. (2001). The Limitations of Bankruptcy Prediction Models: Some Cautions for the Researcher. Review of Quantitative Finance and Accounting, 17:151-166.
Heagerty, P. J., & Zheng, Y. (2005). Survival Model Predictive Accuracy and ROC Curves. Biometrics, 92-105.
Heagerty, P., Lumley, T., & Pepe, M. (2000). Time Dependent ROC Curves for Censored Survival Data and a Diagnostic Marker. Biometrics, 56, 337-344.
Jackson, R. H., & Wood, A. (2013). The performance of insolvency prediction and credit risk models in the UK: A comparative study. The British Accounting Review, 183 -202.
James, G., Witten, D., Hastie, T., & Tibshirani, R. (2013). An Introduction to Statistical Learning with Applications in R.
Kim, M.-J., & Kang, D.-K. (2010). Ensemble with neural networks for bankruptcy prediction. Expert Systems with Applications, 37(4), 3373-3379.
Lin, F., Yeh, C.-C., & Lee, M.-Y. (2011). The use of hybrid manifold learning and support vector machines in the prediction of business failure. Knowledge-Based Systems, 95-101.
Martínez-Camblor, P. (Diciembre de 2007). Comparación de pruebas diagnósticas desde la curva ROC. Revista Colombiana de Estadística, 30(2), 163 a 176.
Martínez-Camblor, P. (2007). Comparación de pruebas diagnósticas desde la curva ROC. Revista Colombiana de Estadística, 30(2), 163 a 176.
Ministerio de Comercio, Industria y Turismo y la Superintendencia de Sociedades. (2007). NUEVO RÉGIMEN DE INSOLVENCIA EMPRESARIAL. Bogotá, Colombia.
Mogensen, U. B., Ishwaran, H., & Gerds, T. A. (2012). Evaluating Random Forests for Survival Analysis Using Prediction Error Curves. Journal of Statistical Software, 50(11), 1-23.
Ortiz, A. T. (2010). Curvas ROC para Datos de Supervivencia. Aplicación a Datos Biomédicos. Santiago de Compostela: Universidad de Santiago de Compostela.
Palmer Pol, A. L. (1993). Modelo de regresión de cox: ejemplo numérico del proceso de estimación de parámetros. Psicothema, 5(2), 387-402. doi:http://www.redalyc.org/articulo.oa?id=72705214
Partington, G., & Kim, M. H. (2008). Modeling Bankruptcy Prediction Using Cox Regression Model with Time-Varying Covariates. Available at SSRN: https://ssrn.com/abstract=1101876 or http://dx.doi.org/10.2139/ssrn.1101876.
Pereira, J. (2014). Survival Analysis Employed in Predicting Corporate Failure: A Forecasting Model Proposal. Canadian Center of Science and Education.
Royston, P. (2011). Estimating a smooth baseline hazard function for the Cox model.
Shin, K.-S., Lee, T. S., & Kim, H.-j. (2005). An application of support vector machines in bankruptcy prediction model. Expert Systems with Applications, 127-135.
Shumway, T. (2001). Forecasting Bankruptcy More Accurately: A Simple Hazard Model. The Journal of Business, 74(1), 101-124.
Simon, N., Friedman, J., Hastie, T., & Tibshirani, R. (2011). Regularization Paths for Cox's Proportional Hazards Model via Coordinate Descent. Journal of Statistical Software, 30(5), 1-13. Obtenido de http://www.jstatsoft.org/
SUPERINTENDENCIA DE SOCIEDADES. (2015). INFORME AUDIENCIA PÚBLICA RENDICIÓN DE CUENTAS 2015. Bogotá, Colombia.
Tibshirani, R. (1995). The lasso method for variable selection in the cox model. Toronto, Ontario, Canada: Department of Preventive Medicine and Biostatistics and Department of Statistics, University of Toronto.
Valencia, C., Cabrales, S., García, L., Ramírez, J., & Calderón, D. (2016). Generalized additive model with embedded variable selection for bankruptcy prediction: The case of the retail industry in Colombia. Working paper. Bogotá, Colombia.
Wang, G., & Ma, J. (2012). A hybrid ensemble approach for enterprise credit risk assessment based on Support Vector Machine. Expert Systems with Applications, 5325-5331.
Wilson, R., & Sharda, R. (1994). Bankruptcy prediction using neural networks. Decision Support Systems, 545–557.
Wood, S. (2003). Thin-plate regression splines. Journal of the Royal Statistical Society, 65(1), 95-114.
Wood, S. (2011). Fast stable restricted maximum likelihood and marginal likelihood estimation of. Journal of the Royal Statistical Society, 73(1), 3-36.
Wood, S. N. (2006). Generalized Additive Models: an introduction with R. Chapman and Hall/CRC.
Wu, Y. (2012). ELASTIC NET FOR COX’S PROPORTIONAL HAZARDS MODEL WITH A SOLUTION PATH ALGORITHM. Statistica Sinica, 22, 271-294. doi:http://dx.doi.org/10.5705/ss.2010.107
1. Estadística y Magister en Inteligencia Analítica. Profesional especializado Dirección de Investigación y desarollo, Superintendencia Financiera de Colombia, Bogotá, Colombia. Correo electrónico: y.castro@uniandes.edu.co
2. Ingeniero Eléctrico y Magister en Inteligencia Analítica. Coordinador de análisis, División mejora de las operaciones comerciales, CODENSA S.A. ESP, Bogotá, Colombia. Correo electrónico: ca.huertas@uniandes.edu.co
3. Ingeniero de Sistemas y Magister en Inteligencia Analítica. Socio de negocio de Analytics, MetLife Colombia seguros de vida S.A., Colombia. Correo electrónico: ce.obando10@uniandes.edu.co
4. PhD en Ingeniería industrial con especialización en estadística, Magister en Estadística y Magister en Ingeniería industrial. Profesor del Departamento de Ingeniería Industrial. Universidad de os Andes, Bogotá, Colombia. Correo electrónico: cf.valencia@uniandes.edu.co
5. En este documento se presentan las razones financieras en inglés, con el fin de mantener su integralidad y entendimiento con respecto a los estudios referenciados.
6. Procesador 2.40 GHz, Memoria RAM 4Gb. Sistema Operativo 32 bits