

 Vol. 39 (Nº 52) Ano 2018. Pág. 29
Vol. 39 (Nº 52) Ano 2018. Pág. 29
Suziê Maria de ALBUQUERQUE 1; Ana Carolina Costa PEREIRA 2; Verusca Batista ALVES 3
Recebido: 11/07/2018 • Aprovado: 02/10/2018 • Publicado 28/12/2018
3. A contagem e o cálculo de quantidades com base no manuseio do ábaco: histórias e interpretações
4. Gerbert de Aurilac: o ábaco e a inserção dos algarismos hindu arábicos na Europa Medieval
RESUMO: O presente artigo aborda um instrumento histórico datado de 976, o Ábaco de Gerbert. Realizou-se uma pesquisa documental a partir do texto Regula de Abaco Computi (1867) no qual, os aspectos históricos apresentaram exemplos práticos aritméticos com as regras da Idade Média. Tal estudo conduz à reflexão sobre o ensino dos métodos de cálculos utilizados atualmente na educação matemática, oportunizando um diálogo entre passado e presente, de maneira que influencie as práticas didáticas escolares. |
ABSTRACT: This article deals with a historical instrument dating from 976, the Gerbert’s Abacus. A documentary research was made from the text Regula de Abaco Computi (1867) in which, the historical aspects presented practical arithmetical examples with the rules of the Middle Age. This study leads to reflection on the teaching of the calculation methods currently used in mathematics education, providing opportunities for a dialogue between past and present, in a way that influences school didactic practices. |
Alguns estudos a nível nacional e internacional vêm mostrando preocupação com o ensino de conceitos matemáticos vinculado a história da matemática, de modo a proporcionar possibilidades de articulação entre a história com o ensino e a aprendizagem da matemática [4] . A história da matemática como área de conhecimentos nos revela potencialidades didáticas e pedagógicas, que segundo Baroni, Teixeira e Nobre (2004) contribuem expressivamente para a melhorias no ensino de matemática. Dentre elas podemos destacar de forma mais abrangente a compreensão do desenvolvimento das ciências e da matemática com visão não linear, contrariando a lógica tradicional do desenvolvimento histórico das ciências, até então disseminada.
Dentre as várias possibilidades de construir uma interface entre a história e o ensino de matemática, que envolve principalmente a construção do conhecimento matemático encontra-se a proposta vinculada ao Grupo de Estudo e Pesquisa, HEEMa (História e Epistemologia na Educação Matemática) da Pontifícia Universidade Católica de São Paulo (PUCSP) coordenado pelo Prof. Fumikazu Saito (PUC/SP) e pela Profa. Dra. Marisa da Silva Dias (UNESP/Bauru) que abrange uma historiografia atualizada por meio de uma descrição das esferas contextual, historiográfica e epistemológica, seguindo uma vertente pedagógica.
Para Saito e Dias (2013, p.91-92) interface [5] é "um conjunto de ações e produções que promova a reflexão sobre o processo histórico da construção do conhecimento matemático para elaborar atividades didáticas que busquem articular história e ensino de matemática". Isto é, um estudo que envolve aspectos historiográficos [6] e didáticos, no qual há um diálogo entre passado e presente, nos permite essa reflexão sobre o desenvolvimento dos conteúdos, de modo que por fim, essa interface atinja a sala de aula por meio de atividades.
Desse modo, construir uma interface requer aproximar as duas áreas de conhecimento, no caso a história da matemática e a educação matemática, uma vez que ambas possuem objetos de investigação específico e bem definido, não podendo sobrepô-los. Esse diálogo entre as duas áreas pode ser realizado para a partir da construção de uma interface.
Com essa linha de raciocínio, adotamos um olhar historiográfico atualizado que, segundo Saito (2016) não tem como foco o conhecimento matemático em si, nem os procedimentos, métodos, técnicas ou algoritmos, mas o processo em que estes estão contextualizados, fazendo emergir outras questões na historicidade, como o processo de construção do conhecimento matemático. Destacando que “toda narrativa da história da matemática é historicamente orientada” (SAITO, 2015, p.21). Este trabalho enquanto narrativa histórica não é neutro e se influencia por diferentes fatores ligados à concepção de ciência de quem escreve a história, apresentando o viés educacional.
Para construir uma interface, o emprego de documentos históricos [7] é essencial para a efetivação de pesquisas que são direcionadas a sala de aula de matemática. Entretanto, é necessário tomar cuidado ao incorporá-lo no ensino, pois sua utilização está atrelada à leitura e à interpretação e ao possível tratamento didático, o que requer tempo e dedicação, visto que demanda uma concepção detalhada do contexto em que foram escritos. É relevante destacar que o tratamento das informações contidas nos textos históricas deve ser refletido e “o pesquisador deve ter cuidado especial, pois a obra possui ideias entrelaçadas de outros autores e, mesmo examinando minunciosamente, algumas questões podem ficar sem resposta” (PEREIRA; PEREIRA, 2015, p. 70).
Dessa forma, a escolha do texto em que irá ser estudado da construção da interface é muito importante e é a partir dele que o pesquisador faz dois movimentos. O primeiro movimento está relacionado com o pensamento na formação do conceito matemático. Ao escolher um documento de um determinado período, percebe-se a presença da matemática, olhando com o conhecimento de hoje, sobrepondo conhecimento da época estudada, para compreender o que está escrito nesses textos (narrativa anacrônica). Nesse ponto, a historiografia tradicional pode ser utilizada.
O segundo movimento se refere ao contexto no qual os conhecimentos matemático foram desenvolvidos, isto é, observar agora o conteúdo matemático, método e os motivos por trás da escrita do documento, contextualizando na época em que foi elaborado e, portanto, considerando todas as características de ordem matemática, técnica e epistemológica como propõe uma historiografia contemporânea.
A partir desses movimentos, um conjunto de atividades podem ser confeccionadas, que tem o intuito de “refletir o processo da produção do conhecimento que, dependendo da intencionalidade do educador, poderá ser orientada para diferentes propostas de ensino” (SAITO; DIAS, 2013, p 101). Para esses autores as atividades podem ser organizadas em três etapas inter-relacionadas: o tratamento didático do documento; a intencionalidade e plano de ação; e o desenvolvimento .
Desse modo, apresentamos neste trabalho um estudo sobre o texto Regula de AbacoComputi, de autoria do matemático Gerbert de Aurillac (946 – 1003), um documento primário que faz parte da coletânea de escritos deste autor e que foi publicada por Olleris (1867). Outros textos também foram consultados como os trabalhos de Chasles (1843) e Ferreira (2008) que estudaram o referido tratado, escrito por volta de 976, na Itália. A proposta delineada aqui nesse estudo visa descrever o primeiro movimento da interface, que está direcionado a esferas contextual e historiográfica que envolve o tratado, principalmente considerando os contextos sociais, políticos e religiosos que influenciaram a aplicação dos algarismos hindu-arábicos por meio do manuseio do Ábaco de Gerbert.
O ábaco como instrumento de registro e cálculos matemáticos é conhecido desde a antiguidade, tendo em vista que “a forma mais primitiva de ábaco pode ter sido uma bandeja de areia marcada, de onde vem o nome genérico (do Grego abax, para “bandeja de areia”). Formas de ábaco eram usadas pelos antigos egípcios, gregos, romanos, hindus e pessoas de quase todo o oriente” (AZEVEDO, 2006, p.2). Ou seja, o ábaco se apresenta como elemento de cálculo em diversas culturas, sendo introduzido e reinventado de acordo com as necessidades de cada uma delas no momento histórico vivenciado.
Este artigo encontra-se dividido em duas partes. Na primeira parte discorremos sobre a contagem e o cálculo de quantidades com base no manuseio do ábaco, buscando histórias e interpretações na idade média. Na segunda, descrevemos brevemente sobre o autor do tratado, Gerbert de Aurillac, e a inserção do ábaco e dos algarismos hindu arábicos na Europa Medieval de acordo com uma técnica de multiplicação e outra de divisão praticada na época, tendo como inspiração o texto histórico Regula De Abaco Computi. Evidenciando assim a possibilidade da elaboração de atividades com vistas à utilização desses métodos de cálculo para o ensino de aritmética, indicando a construção de interface entre a história e o ensino.
O presente estudo foi desenvolvido com a metodologia de pesquisa documental, pois “vale-se de materiais que não receberam ainda um tratamento analítico, ou que ainda podem ser reelaborados de acordo com os objetivos da pesquisa” (GIL, 2008, p.50). Tendo em vista que é pretendido compreender o uso do Ábaco de Gebert a partir dos indícios coletados na obra original Regula De Abaco Computi.
Para tanto, após o conhecimento da existência do instrumento Ábaco de Gerbert e das buscas preliminares indicarem a existência de um texto histórico para subsidiar o manuseio do Ábaco, as autoras tiveram acesso à obra digitalizada na Biblioteca francesa Gállica na qual constava o arquivo digitalizado, escrito em latim.
Com o intuito de fazer uma breve contextualização histórica que embasasse o entendimento dos processos de elaboração dos conhecimentos matemáticos estudados, passou-se a indicar traços de pesquisa bibliográfica, realizando um levantamento das produções de educadores matemáticos e historiadores que versam sobre o assunto, pois esta pesquisa também foi “desenvolvida com base em material já elaborado, constituído principalmente de livros e artigos científicos” (GIL, 2008, p.50).
No entanto, o caráter documental deste artigo sobrepõe o bibliográfico, tendo em vista que a partir do estudo da fonte primária Regula De Abaco Computi e dos trabalhos secundários as autoras produziram adaptações do Ábaco, representadas como forma de imagem, retificando o aspecto didático e pedagógico deste trabalho.
Ao longo da história, evidências de que o homem realiza princípios de contagem são identificadas em registros por meio de pinturas e artefatos estudados por paleontólogos e pesquisadores da área de antropologia. Esses estudos podem colaborar na compreensão dos processos de desenvolvimento e construção dos saberes matemáticos produzidos em sociedade, a partir das necessidades cotidianas que emergem de questões ligadas ao instinto de sobrevivência e de melhoria da qualidade de vida das pessoas em determinado período histórico, atendendo aos contextos sociais, econômicos, políticos, religiosos, dentre outros, vivenciados pela sociedade de cada época.
Os processos históricos de construção do conhecimento matemático têm um longo e enviesado percurso, portanto sem linearidade e constituindo-se de obra coletiva de várias culturas, a partir da contribuição de centenas de indivíduos que “movidos pelas necessidades concretas, construíram coletivamente a matemática que conhecemos hoje” (FIORENTINI, 1995, p.31).
Nessa perspectiva, podemos destacar que a matemática do passado pode ser acessada para se compreender os processos de elaboração das técnicas de contagem vivenciadas pelo ser humano no decorrer dos tempos, de acordo com a cultura e a sociedade em que faz parte. Tendo em vista que “a contagem é, com efeito, um atributo exclusivamente humano, diz respeito a um fenômeno mental muito complicado, intimamente ligado ao desenvolvimento da inteligência” (IFRAH, 1998, p.44).
Com base na história da contagem matemática realizada por indivíduos com práticas socialmente constituídas, compreendendo a manipulação concreta de objetos da natureza e a posterior e gradativa abstração desses procedimentos e mecanismos, pode-se considerar o ábaco como instrumento matemático de contagem e de cálculo, superando sua origem, pois:
As pedras estão particularmente na origem dos ábacos e dos contadores mecânicos, estes instrumentos que o homem inventou no dia em que precisou fazer cálculos cada vez mais complicados e que tanto usou quando ainda não dispunha do cálculo escrito por meio dos algarismos arábicos (IFRAH, 1998, p.117).
Com relação à contagem e realização de cálculos aritméticos, quando ainda não se tinha conhecimento das técnicas e algoritmos que conhecemos atualmente, o ábaco constituiu-se como considerável instrumento de registro e cálculos matemáticos. Vale ressaltar que “do ponto de vista histórico o instrumento está alocado entre a teoria e o experimento, entre as considerações de ordem abstrata e concreta, ou ainda, entre critérios racionais e empíricos de validação do conhecimento (SAITO, 2016, p.11)”.
Saito (2016) considera ainda que os instrumentos matemáticos antigos não são neutros na construção do conhecimento matemático ao longo da história, pois estes dão suporte ao processo de desenvolvimento da matemática. A partir desse pensamento podemos revelar os mecanismos de funcionamento da “máquina” – o ábaco, levando o aprendiz a compreender melhor a elaboração do conhecimento matemático e, além disso, a que este conhecimento está vinculado.
A seguir serão explorados os contextos que emergem das construções aritméticas ao longo dos tempos para se ressignificar os caminhos traçados pelos povos ao logo da história de desenvolvimento da aritmética.
A relação entre a prática proporcionada pelo conhecimento matemático e a aplicação do ábaco é dada destaque a seguir a partir de um registro por imagem localizado na obra Marguerita Philosophica de Reisch (1503). Esta produção consiste em uma enciclopédia, contendo informações sobre a Dialética, Retórica, Aritmética (Teórica e Prática), Música (Teórica e Prática), Geometria (Especulativa e Prática), Astronomia e Filosofia (Natural e Moral). Ou seja, contém em síntese os conhecimentos que estavam em vigor e que deveriam ser socializados com os nobres da época, tendo em vista que a exploração de novas terras, a navegação e o domínio de povos necessitava de profissionais preparados para compreender o convívio em sociedade e com a natureza.
Segundo Miranda (2008), Reisch havia preparado a Enciclopédia Margarita Philosophica (figura1) para ser publicada desde 1496, no entanto o texto sofreu algumas alterações e foi publicada apenas na data mencionada anteriormente.
Figura 1
Senhora aritmética na obra Margarita Philosophica

Fonte: Reisch (1503, p.159).
A figura 1 representa um duelo entre os matemáticos Pitágoras e Boécio. Pitágoras manipula o ábaco, enquanto o matemático Boécio realiza operações matemáticas utilizando algarismos. O ábaco é apresentado nessa ilustração como um mecanismo de aplicação prática, com o qual os números podem ser manipulados de forma concreta. No contexto da imagem pode ser observada a concorrência entre ambos os métodos. Observando melhor a obra visualiza-se a:
Gravura em madeira ornando a Margarita Philosophica de Gregorius Reisch (Ed. Freiburg, 1503). Senhora Aritmética (simbolizada pela mulher de pé no centro da gravura) decide o debate: a querela dos abacistas e dos alegoristas não terá mais sentido doravante. A aritmética olha na direção do calculador que efetua suas operações com o zero e os algarismos “arábicos” (algarismos de que seu vestido está ornado) (OLIVEIRA, 2008, p.50).
Vale ressaltar que no ano 1503 quando a obra Margarita Philosophica foi escrita no mundo europeu que vivia momento com “descobertas” de novos mundos e se abriam mercados, novas terras a explorar. Certamente, houve a necessidade de reinventar as formas de lidar com as transações comerciais que se configuravam cada vez mais dinâmicas na época. A aritmética na figura feminina expressa sua preferência pela simplificação dos cálculos aritméticos fundamentais no cotidiano da sociedade europeia da época.
No tecido histórico que compõe a elaboração, aplicação e raciocínios matemáticos a partir do ábaco é conveniente neste trabalho voltar um pouco mais no tempo e conhecer a atuação do matemático Gerbert de Aurilac (nascido entre 940 e 945 d.C), segundo Ferreira (2008) para relacionarmos com a questão levantada na imagem anterior: os algarismos hindu-arábicos, o manuseio do ábaco e a importância desses dois mecanismos no desenvolvimento do conhecimento matemático no que diz respeito a contagem e operações aritméticas.
Com o objetivo de vincular informações sobre os processos de desenvolvimento da aritmética vamos trazer à tona a história do religioso e matemático Gerbert de Aurilac que haveria de se tornar Silvester II, papa da Igreja Católica (999 d.C a 1003 d.C). Antes de se tornar Papa, Gerbert viveu em Aurilac, cidade que pertencia à França e era na época um centro de conhecimentos matemáticos, tendo contato com estudiosos da aritmética, geometria, astronomia e música, tendo contato com culturas mulçumanas, contribuindo para a socialização de saberes e construção de novos conhecimentos.
No movimento de consolidação e elaboração de conhecimentos, Gerbert escreveu obras matemáticas como: "De ábaco Computi, De numerumdivivione, Geometria, carta a Adebold sobre o cálculo da área de triângulos, a Constantin sobre a esfera, [...] várias outras cartas” (FERREIRA, 2008, p.45). Ou seja, houve considerável número de produções matemáticas por parte de Gerbert e seus contemporâneos que podem nos ajudar a compreender melhor os processos de construção do conhecimento matemático a partir dessas obras, que se tornaram fontes históricas e constam de registros que expressam a forma de pensar matematicamente de um povo, em um tempo e espaço.
De acordo com Ferreira (2008), Gerbert juntamente com seus seguidores elaboraram métodos próprios de multiplicação e divisão adotando o sistema posicional do ábaco. No entanto, pelo fato de utilizar uma simbologia própria para cada quantidade, os algarismos hindu-arábicos e a representação deles no ábaco, foi pouco compreendido na época por introduzir entes abstratos ao sistema concreto e manipulável do ábaco.
Ferreira (2008) traz ainda em seu trabalho um estudo sobre a obra de Michel Chasles (1793-1880), intitulada “Historie de l’Aritmétique: Explication des Traités de l’Ababu, et particullèrement du Traité de Gerbert em Paris” este autor defendeu a tese de que os algarismos hindu arábicos já eram utilizados na Europa muito antes de Gerbert, com base no livro de Geometria, de autoria do matemático Boécio (480 a 524 d.C). Mesmo assim:
Hoje se tem como certo que foi Gerbert que introduziu na Europa o sistema de numeração arábico, quando escreveu seu tratado – muito confuso para a época – do uso do ábaco. Mas é a partir do início do século XIII, graças a influência determinante de um grande matemático italiano, Leonardo de Pisa (Por volta de (1170 – 1250), mais conhecido como Fibonacci, e do seu livro Liber Abaci (1202), que se tornou conhecido em toda a Europa cristã e o sistema numérico que utilizamos até hoje. Mesmo tendo no título a palavra ábaco, não se assemelhava aos tratados de aritmética da tradição de Gerbert e seus discípulos, pois Fibonacci explicava as regras do cálculo escrito usando o zero e as nove cifras arábicas, usando a regra posicional (FERREIRA, 2008, p.45)
Portanto, Gerbert não tinha ainda um símbolo para representar o zero. Em seu ábaco era necessário apenas permanecer com o espaço vazio. No entanto, o cálculo no papel ou outro material para escrita conduziu à representação do zero em forma de algarismo, sofisticando os procedimentos matemáticos da época, mas isso aconteceu séculos após os estudos de Gerbert, com a atuação de Leonardo Fibonacci que também teve contato com a cultura árabe.
O contexto social, político e religioso da época no qual o ábaco trabalhado por Gerbert se apresentava, era formado pela hostilidade da idade média e as limitações impostas ao desenvolvimento da ciência, especialmente, da formação da matemática como área de conhecimento.
Gerbert foi julgado diferentemente, na Idade Média: era considerado como alquimista e bruxo, que foi buscar sua ciência com os “infiéis” e vendeu sua alma a Lúcifer. Graves acusações que se mantiveram sobre o sábio homem durante séculos, ao ponto de, em 1648, a autoridade pontifícia julgar necessário abrir o túmulo de Silvester II a fim de verificar se os diabos do inferno não se encontravam lá (IFRAH, 1994, p. 360).
A citação de Ifrah (1994) nos remete ao fato de que a Igreja influenciou a não disseminação das ideias de Gerbert, sendo os algarismos hindu-arábicos divulgados e colocados em prática na cultura europeia apenas no século XII, por Leonardo Fibonacci. Alguns estudiosos na história das ciências de nossa época, como Saito (2015), enfatizam:
No que diz respeito às operações aritméticas, latinos medievais não as efetuavam tal como hoje nós as realizamos. A razão para tanto estava relacionada ao sistema de numeração que era adotado naquela época, devemos lembrar que o sistema de numeração era romano e não indo-arábico, que só entrou em vigor no Ocidente latino por volta do século XII, disseminando-se plenamente apenas nos séculos seguintes. Assim, os latinos, que se dedicavam à aritmética prática, ou “logística”, isto é, à arte de calcular, desenvolveram diferentes técnicas auxiliares para realizarem as operações aritméticas. Eles utilizavam basicamente três procedimentos: cálculos com o auxílio dos dedos, de ábacos ou de tabelas com resultados das operações preparadas com antecedência (SAITO, 2015, p.125).
É justamente uma dessas formas de calcular utilizados na idade média que será explorada a seguir, com exemplos práticos de aplicação, considerando os métodos adotados por Gerbert de Aurilac, a partir do uso do ábaco, sendo as quantidades representadas por fichas com símbolos para representar os algarismos de 1 a 9. Iremos aprofundar esse assunto para compreender melhor como funcionam os processos de cálculos atualmente pelos meios que vem sendo colocados em prática, tanto com o uso do ábaco como de algoritmos.
O ábaco de Gerbert foi construído com base em uma tábua ou prancha com marcações em colunas, nas quais representavam agrupamentos de elementos em potências de base 10. Os números a serem representados em cada agrupamento eram representados (quadro 1) por fichas confeccionadas por materiais disponíveis no período, como pedras, chifres de bois, metais, dentre outros.
Quadro 1
Representação com algarismos romanos no ábaco de Gerbert.
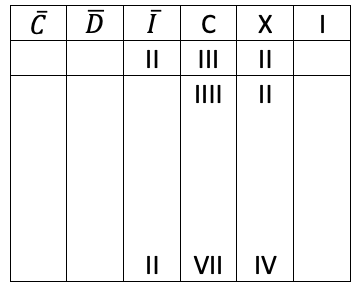
Fonte: Elaborado pelas autoras (2018)
A faixa superior em algarismos romanos indica na ordem crescente da direita para a esquerda: 1, 10, 100, 1000 e 100000. Na parte seguinte do ábaco, segundo Ferreira (2008) eram utilizados valores compostos por unidades para representar as dezenas, centenas, unidades de milhar, todos na base 10 e assim por diante. O exemplo dado nos traz o ábaco registrando 2740, mas esta quantidade era por fim, representada em algarismos romanos, como indica a última inscrição no ábaco apresentado.
A grande contribuição de Gerbert foi de, no lugar de colocar traços ou marcas, tantas quantas fossem necessárias, em cada coluna, construir fichas de chifre de boi e nelas marcar a numeração hindu-arábica que trouxera da Espanha. Assim, numa coluna onde deveria haver, por exemplo, nove traços, colocavam uma só ficha com a representação do número nove (FERREIRA, 2008, p.46).
De acordo com a necessidade de simplificar o mecanismo já existente, Gerbert teve a ideia de associar o conhecimento que trouxe dos árabes (figura 2) a sua prática com o ábaco, propondo a seguinte representação para os algarismos de 1 a 9.
Figura 2
Símbolos utilizados por Gerbert para representar os números

Fonte: Ferreira (2008, p.47)
As produções aritméticas de Gerbert foram registradas em seu tratado Regula de AbacoComputi (976), Ferreira (2008) traz em seu trabalho a análise desta obra a partir de estudos de Chasles (1843). Em seu tratado, Gerbert descreve o ábaco como apresentado anteriormente: em colunas, com inscrições em algarismos romanos, utilizando fichas com os símbolos acima para representar as quantidades. No quadro 2 pode-se verificar um exemplo da representação do número 2740 por meio do ábaco de Gerbert:
Quadro 2
Adaptação do Ábaco de Gerbert

Fonte: Elaborado pelas autoras (2018)
Para Gerbert, este artifício de codificar as quantidades facilitava seu trabalho, porém as pessoas que desenvolviam atividades matemáticas na época as consideravam complicadas para tal exercício. Observe a seguir que na multiplicação no ábaco de Gerbert, ele inseriu o multiplicando logo após a inscrição no topo do ábaco indicando as ordens em algarismos romanos (unidade, dezena, centena, unidade de milhar, ...) e o multiplicador no inferior do ábaco, na última linha.
Na parte central do instrumento dispunha as parciais da multiplicação. Multiplicava-se como fazemos hoje, se estamos operando o multiplicando pelo multiplicador na primeira coluna a direita do ábaco, então é nesta coluna que iniciamos o registro do resultado e assim por diante (quadro 3). A soma das parciais da multiplicação, ou purgatio, como foi denominada por Gerbert era registrada logo após as parciais e acima do multiplicador.
Quadro 3
Multiplicação no Ábaco de Gerbert

Fonte: Elaborado pelas autoras (2018)
Perceba que para assimilar o processo multiplicativo, se faz necessária apropriação da simbologia, além de compreender as regras da operação aritmética. Caso contrário, se torna dificultada a construção das aplicações, já que os símbolos agregam conotação de mistério às quantidades. Para facilitar a compreensão dos leitores deste trabalho apresentamos a seguir um exemplo de divisão de Gerbert no ábaco utilizando os algarismos hindu-arábicos que conhecemos atualmente. Dessa forma, o quadro 4 apresenta um exemplo do funcionamento do Ábaco de Gerbert para a divisão de 345 por 3.
Quadro 4
Divisão no Ábaco de Gerbert
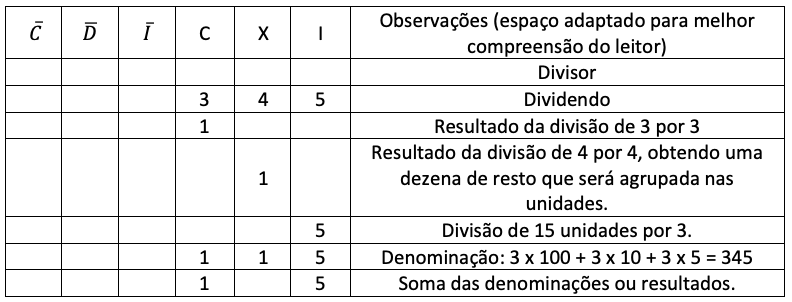
Fonte: Elaborado pelas autoras (2018)
Esse método de divisão é o método denotado como "sem diferença", descrito por Gerbert e que muito se assemelha com o utilizado hoje, como podemos observar. O processo operatório é executado no ambiente do ábaco, deixando claro o fator posicional do nosso sistema de numeração e nos dando pistas da origem e desenvolvimento histórico dos nossos métodos de cálculos. Segundo Ferreira (2008), Gerbert relatou em seu tratado ainda outros métodos de divisão: divisão composta, divisão por diferença, divisão de milhares por centenas com unidades, divisão de centenas, milhares por dezenas, dentre outros.
No entanto, neste trabalho nos detemos em apenas um método como nos exemplos apresentados, uma vez que estes mais se aproximam dos métodos em uso na atualidade e podem colaborar na formação de professores, pois poderão levá-los a compreender o processo de elaboração dos algoritmos adotados, possibilitando que estes profissionais desenvolvam atividades com seus estudantes.
A inserção dos algarismos Indo-arábicos no Ocidente não ocorreu de forma linear e progressista, pois houve momentos na história onde esses algarismos foram propostos, como por Gerbert, mas não houve aceitação da sociedade política e religiosa da época, havendo a difusão desses conhecimentos apenas séculos após, por Leonardo Fibonacci. O que remete a ideia de que houve idas e vindas ao processo de apropriação por parte de um maior número de pessoas, com relação às operações aritméticas adotando os algarismos hindu-arábicos para representar as quantidades.
O processo de construção dos métodos de cálculo aritméticos que conhecemos hoje foi resultado de um longo percurso histórico, desde a utilização do próprio corpo sendo instrumento de representação numérica, objetos e instrumentos matemáticos de registro, até a o uso de materiais manipuláveis para a abstração dos registros escritos dos algarismos por meio de simbologia própria.
A partir desses achados históricos emergiu a importância de compreender os processos de apropriação dos algarismos hindu-arábicos e sua aplicação no uso do ábaco para o desenvolvimento de operações aritméticas na idade média. O ábaco nesta relação, se revelou como marcante instrumento matemático que, por certo período histórico, caiu em desuso, mas que pode ser empregado no Ensino de Matemática através da contextualização histórica para que os professores oportunizem vivências práticas no campo das operações aritméticas, principalmente no sentido de evidenciar para além dos algoritmos.
O conteúdo apresentado neste trabalho, relaciona a primeira etapa da interface descrita inicialmente, no qual realizou-se parte do primeiro movimento, em que se abordou os aspectos históricos e contextuais. A seguir, o estudo se desenvolve para uma investigação sobre o viés epistemológico, formando assim a tríade inicial da interface que, por conseguinte proporciona um conhecimento robusto para se realizar o segundo movimento, também já descrito no início deste artigo.
Portanto, partindo das referências teóricas envoltas a articulação entre a história e o ensino de matemática, entende-se que atualmente o ábaco e a construção do conhecimento matemático que foi construído por meio do instrumento, podem ser empregados na educação matemática colaborando tanto na formação de professores da Educação Básica e, por consequência, na possibilidade de efetivar a aprendizagem de seus estudantes, conduzindo-os na compreensão das propriedades do nosso sistema de numeração posicional e nos métodos de cálculo aritmético.
Assim, este trabalho apresenta indícios de continuidade, pois o primeiro movimento do pensamento encaminhou o estudo dos aspectos epistemológicos do texto histórico em questão, dando início ao segundo movimento do pensamento que inclui a identificação dos métodos e técnicas por trás da elaboração dos conceitos aritméticos explorados. A partir desses dois movimentos, serão elencados os elementos potencialmente didáticos para a elaboração e aplicação de atividades junto a formação de professores do curso de pedagogia em uma universidade brasileira, no estado do Ceará.
AZEVEDO, O. C. S. Operações matemáticas com o Soroban (ábaco japonês). Obtido em: http://www.ucb.br/sites/100/103/TCC/22006/OrlandoCesarSiadedeAzevedo.pdf.
BARONI, R. L. S.; TEIXEIRA, M. V.; NOBRE, S. R. (2004). A Investigação Científica em História da Matemática e suas Relações com o Programa de Pós-Graduação Em Educação Matemática. In: BICUDO, M. A. V.; BORBA, M. de C.(Org.). Educação Matemática: pesquisa em movimento. p. 164-185. São Paulo: Cortez.
BELTRAN, M. H. R.; SAITO, F.; TRINDADE, L. dos S. P. (2010). História das ciências: tópicos atuais. São Paulo: Livraria da Física.
BEO, N. (2015). O estudo do Trattato del Radio Latino: Possíveis contribuições para a articulação entre História da Matemática e ensino. (Dissertação de Mestrado). Pontifícia Universidade Católica de São Paulo, São Paulo.
CASTILLO, A. R. M.; SAITO, F. (2016). Algumas considerações sobre o uso do báculo (baculum) na elaboração de atividades que articulam história e ensino de matemática. In: J. Flores Salazar & F. Ugarte Guerra (eds.). Investigaciones en Educación Matemática. p. 237-251. Lima: Fondo Editorial PUCP.
CHAQUIAM, M. (2017). Ensaios Temáticos História e Matemática em sala de aula. Belém: Sbem/Sbem-PA.
CHASLES, M. (1843). Histoire de l´Arithmétique: dévelloppement et détails sur divers du système de l´Abacus. Paris: l´ Academie des Sciences.
FERREIRA, E. S. (2008). O ábaco de Silvester II. RBHM, 8(15), 43-45.
FIORENTINI, D. (1995). Alguns modos de ver e conceber o ensino da Matemática no Brasil. ZETETIKÉ, 3(1), 1-38.
FURINGHETTI, F. et al. (2008). The role of the history of mathematics in mathematics education. In: INTERNATIONAL CONGRESS ON MATHEMATICAL EDUCATION, 11., 2008, Monterrey. (pp. 1-4). Monterrey. Obtido em: http://www.mathunion.org/fileadmin/ICMI/files/Digital_Library/ICMEs/TSG_23_Report_BB_FF.pdf
FURINGHETTI, F.; JAHNKE, H. N.; MAANEN, J. V. (2006). Mini-workshop on studying original sources in mathematics education. Oberwolfach Reports 3(2),1285-1318.
GIL, A. C. (2008). Como elaborar projetos de pesquisa. 4. ed. São Paulo: Atlas.
GRATTAN-GUINNESS, I. (2005). History or heritage? An important distinction in mathematics and for mathematics education. In: VAN BRUMMELEN, G.; KINYON, M. (Org.). Mathematics and the historian's craft: the Kenneth O. May lectures. p. 7-21. New York: Canadian Mathematical Society: Springer.
IFRAH, G. (1994). HistoirUniversale des chiffre. Paris: Èditions Robert Laffontp. Tradução de Eduardo Sebastinani Ferreira.
IFRAH, G. (1998). Os Números: a história de uma grande invenção. 90. Ed. Editora Globo. Tradução Senso, Stella M. de Freitas.
JAHNKE, H. N. et al. (2000). The use of original sources in the mathematics classroom. In: FAUVEL, John; MAANEN, Ja. V. (ed). History in mathematics education: the ICMI study. p.291-328. Dordrecht: Kluwer.
JANKVIST, U. T. (2014). On the use of primary sources in the teaching and learning of Mathematics. In: MATTHEWS, M, R. (Ed.). International Handbook of Research in History, Philosophy and Science Teaching. p. 873-907. Dordrecht: Springer.
MASSA ESTEVE, M. R. et al. (2011). Understanding mathematics using original sources: Criteria and conditions. In: BARBIN, Evelyne; KRONFELLNER, Manfred; TZANAKIS, Constantinos (Ed.). History and Epistemology in Mathematics Education: Proceedings of the 6th European Summer University. p. 415-428. Viena: Verlag Holzhausen Gmbh.
MENDES, I. A. (2006). Matemática e investigação na sala de aula: tecendo redes cognitivas na aprendizagem. Natal: Flecha do Tempo.
MENDES, I. A. (2009). Investigação histórica no ensino da Matemática. Rio de Janeiro: Ciência Moderna.
MIGUEL, A.; MIORIM, M. Â. (2004). História na Educação Matemática: Propostas e desafios. Coleção Tendências em Educação Matemática. Belo Horizonte: Autêntica.
MIRANDA, M. (2008). Margarita philosophica (1503): uma cyclopaedia do século XVI. Boletim de Estudos Cássicos, 8(50), 53-59.
MORAES, M. (2017). Setor trigonal: Contribuições de uma atividade didática na formação de conceitos matemáticos na interface entre história e ensino de matemática. (Dissertação de mestrado profissional). Universidade Estadual Paulista. Bauru.
OLLERIS, A. (1867). Oeuvers de Gerbert Pape sous le nom de Sylvestre II: collationnées sur les manuscrits. Paris: LIBR. ÉDITEU.
OLIVEIRA, D. S. (2008). Números e sistema de numeração. (Monografia de Especialização). Obtido em: http://sistemas.eel.usp.br/bibliotecas/monografias/2008/MMA08005.pdf.
PEREIRA, A. C. C.; PEREIRA, D. E. (2015). Ensaio sobre o uso de fontes históricas no ensino de matemática. Rematec, 10(18), 65-78.
PEREIRA, A. C. C.; SAITO, F. (2018). Os instrumentos matemáticos na interface entre história e ensino de matemática: compreendendo o cenário nacional nos últimos 10 anos. In: Seminário Cearense de História da Matemática, (pp. 1-12). Fortaleza: Eduece.
PINSKY, C. B. et al. (2006). Fontes históricas.2. ed. São Paulo: Contexto.
REISCH, G. (1503). Margarita philosophica. Freiburg im Breisgau: Johannen Schottum.
SAITO, F.; DIAS, M. da S. (2013). Interface entre história da matemática e ensino: uma atividade desenvolvida com base num documento do século XVI. Ciência & Educação, 19(1), 89-111.
SAITO, F. (2014). Instrumentos matemáticos dos séculos XVI e XVII na articulação entre história, ensino e aprendizagem de matemática. Rematec, 16(9), p. 25-47.
SAITO, F. (2015). História da matemática e suas (re)construçõescontextuais. São Paulo: Editora Livraria da Física.
SAITO, F. (2016a). Construindo interfaces entre história e ensino da matemática. Ensino da Matemática em Debate, 3(1), 3-19.
SAITO, F. (2016b) História e Ensino de Matemática: Construindo Interfaces. In: SALAZAR, Jesús Flores; GUERRA, Francisco Ugarte. Investigaciones en Educación Matemática. p. 253-291, Lima: PUCP.
TZANAKIS, C. et al. (2002). Integrating history of mathematics in the classroom: an analytic survey. In: FAUVEL, J.; MAANEN, J. van. History in Mathematics Education: The ICMI Study. 201-240. Dordrecht/Boston/London: Kluwer Academic Publishers.
XAVIER, E. da S. (2010). O uso das fontes históricas como ferramentas na produção de conhecimento histórico: a canção como mediador. Antíteses, 3(6). 1097-1112.
1. Mestranda do Programa de Pós-Graduação em ensino de ciências e matemática do Instituto Federal de Educação, Ciência e Tecnologia do Ceará – IFCE. E-mail: suziealbuquerque@hotmail.com
2. Docente da Universidade Estadual do Ceará – UECE e do Programa de Pós-Graduação em Ensino de Ciências e Matemática do Instituto Federal de Educação, Ciência e Tecnologia do Ceará – IFCE. E-mail: carolina.pereira@uece.br
3. Mestranda do Programa de Pós-Graduação em Ensino de Ciências e Matemática do Instituto Federal de Educação, Ciência e Tecnologia do Ceará – IFCE. E-mail: veruscah.alves@gmail.com
4. Sobre articulação entre história e ensino de matemática, consulte: Tzanakis et al (2002), Grattan-Guinness (2005), Furinghetti (2008), Miguel; Miorim (2004), Mendes (2006, 2009) e Chaquiam (2017), D’Ambrósio (2007), Saito (2016) e Pereira e Saito (2018).
5. Sobre construção de interface entre história e ensino de matemática, consulte: Saito (2014, 2015, 2016ª, 2016b), Saito e Dias (2013), Beo (2015), Castilho e Saito (2016), Moraes (2017).
6. Define-se historiografia como a escrita da história. Para Saito (2015) há duas vertentes histográficas a serem consideradas para compreender o estudo histórico, a tradicional e a atualizada. Porém, para construção de uma Interface entre história e ensino, é necessário apoiar na vertente atualizada. Para saber mais, vide Saito (2015); Beltran, Saito, Trindade (2010, p. 47-71).
7. Sobre fontes e documentos históricos, consulte: Massa Esteve (2011), Xavier (2010), Pinsky (2006), Tznakis el al (2000), Furinghetti, Jahnke, Maanen (2006), Jahnke (2000), Jankvist (2014), Pereira e Pereira (2015)
8. Para um detalhamento melhor dessas etapas ver Saito e Dias (2013).