ISSN 0798 1015

Vol. 39 (Nº 50) Año 2018. Pág. 18

Análisis de redes de sistemas de bicicletas públicas en ciudades latinoamericanas usando teoría de grafos

Network analysis of public bike systems at latin-american cities using graph theory

Hugo Fernando BRAVO Artunduaga 1; Angela Mariana ROJAS Cruz 2; Ciro JARAMILLO Molina 3; Jackeline MURILLO Hoyos 4

Recibido: 29/06/2018 • Aprobado: 15/09/2018 • Publicado 15/12/2018

Contenido

1. Introducción

2. Metodología

3. Resultados y discusión

4. Conclusiones

Referencias bibliográficas

1. Introducción

Los habitantes de un determinado territorio necesitan desplazarse todos los días para llegar a su destino, ya sea al trabajo, escuela o adquisición de un servicio. Este traslado se puede llevar a cabo caminando, utilizando vehículos no motorizados (bicicletas), o vehículos motorizados (autobuses, automóviles) (CAF, 2011 P.15). La necesidad de movilizarse es indispensable de acuerdo a los requerimientos de la población, pero la falta de equidad social hace que se presenten problemas de desigualdad a la hora de desplazarse y acceder a los servicios de transporte. Por tal razón, se debe hacer una buena planificación de movilidad para alcanzar la sustentabilidad (Medina y Veloz, 2012).

La inequidad y la falta de estructuración en miras del desarrollo sostenible, ha hecho que en ciudades Latinoamericanas la movilidad se relacione con ciertas características. El incremento del parque automotor, por ejemplo, posiciona a Ciudad de México como una de las ciudades más contaminadas y contaminantes del mundo emitiendo 25.600 toneladas de CO2 al día, por encima de Buenos Aires, Sao Paulo, Río de Janeiro y Bogotá con 23.000, 22.500, 15.500 y 8.000 respectivamente. De acuerdo a la población, Río de Janeiro es la ciudad que más utiliza el transporte motorizado con un total de 92% de sus habitantes, mientras que Buenos Aires lo hace en un 91%, Bogotá 85%, México 76% y Sao Paulo 66%; sin contar con que estás ciudades se destacan por sus altas inversiones en infraestructuras de transporte (CAF, 2011).

Dados los niveles de contaminación presentes en diferentes ciudades latinoamericanas, los gobiernos y las instituciones líderes en definición de políticas y estrategias para contrarrestar esta situación desfavorable han optado por la implementación de sistemas de transporte público masivo y transporte público de bicicletas que son amigables con el medio ambiente (Naciones Unidas, 2009).

Los sistemas de transporte público de bicicletas (STPB) deben ser planificados de la misma manera que se hace con cualquier sistema, sin escatimar esfuerzos en su planificación e implementación. Esto debe tomar un tiempo considerable teniendo en cuenta los factores que intervienen en su diseño ya sean físicos u operacionales. (Pardo et al., 2010).

Existen herramientas para analizar la estructura de los sistemas de transporte conservando los criterios de planificación. Con dichos análisis es posible evaluar el comportamiento de redes viales de forma individual para una comparación posterior con redes viales de otros sistemas de transporte. La teoría de grafos es una herramienta usada para el análisis de las redes viales a partir de su topología, basándose en indicadores que evalúan el funcionamiento de un sistema, permitiendo comparaciones entre pares. Para el caso de esta investigación, alternativas de transporte público sostenible en ciudades latinoamericanas.

A continuación, se describen las fases metodológicas que se abordaron para el análisis de redes de STPB haciendo uso de la teoría de grafos.

2.1. Identificación de índices para analizar las estructuras de las redes de los STPB

La identificación de los índices para el desarrollo de este proyecto se realizó a partir de la consulta bibliográfica de estudios y proyectos que involucran el análisis de la topología de las redes de transporte. De esta manera se tuvieron en cuenta dos aspectos para la evaluación: medidas de conexión (estado y forma de las redes de infraestructura) y medidas de accesibilidad. La descripción de los modelos implementados para el análisis se describe a continuación.

La teoría de grafos se utiliza para resolver preguntas relacionadas con las propiedades y la función de las redes en campos de aplicación como la ecología del paisaje, la sociología, las ciencias informáticas y el transporte. La teoría de grafos estudia las propiedades de los grafos que consisten en un conjunto de nodos () y un conjunto de enlaces (), donde cada enlace está determinado por dos vértices, es por ello que está relacionada estrechamente con la topología de las redes (Taczanowska et al.,2014). Los nodos pueden ser de tipo terminal si se ubican al final de un enlace, tipo intersección si se ubican en el cruce de dos o más enlaces, tipo ficticio cuando hay cambio de sentido en un enlace, o cuando se utilizan para conservar la geografía de la red.

Para evaluar la conexión en la red de cada sistema, se define el análisis de indicadores para conocer el estado y la forma de los mismos. Cardozo en el 2009, evaluó el número ciclomático (u), e índices Alfa (a), Gamma (j) y Beta (b) para conocer el estado de una red de infraestructura de transporte público, obteniendo resultados que mostraban el comportamiento con relación a la conectividad.

El número ciclomático (1) representa el número máximo de ciclos que presentan las redes. El índice Alfa (2) muestra el porcentaje de circuitos que tienen las redes, del total posible. El índice Gamma (3) denota el porcentaje de arcos de la red, de los posibles, y el índice Beta (4) muestra la complejidad de las redes, de manera que si este valor es 1, la red formaría un solo circuito, mientras que si es menor o mayor a la unidad, las redes son inconexas o complejas, respectivamente.

Donde e son los arcos o enlaces, v son los nodos, y p son los subgrafos.

Para describir la forma de las redes, se consideraron los índices grado de cohesión (C_st), densidad de la red (ND) e indicador de cobertura (s). El grado de cohesión (5), permite identificar el costo de la red o la longitud total de ésta, haciendo una relación entre los nodos, los enlaces y el mayor número de conexiones (Potrykowski y Taylor, 1984). El límite mínimo de conexiones se calcula fraccionando el número de nodos sobre 2. Si se acerca a (n/2) tiende a presentar cohesión mínima y si se acerca a 1, tiende a presentar cohesión máxima. La densidad (6), mide la cantidad de espacio que ocupa una red, teniendo en cuenta la longitud de los enlaces y la superficie (Rodrigue, et al, 2013). El indicador de cobertura (7), calcula la cobertura total de la red, teniendo en cuenta la longitud, el número de estaciones y distancia entre estas; entre más bajo sea este valor, mayor cobertura local tiene la red (Derrible y Kennedy, 2010).

El número asociado (NS) y el índice Shimbel, son dos medidas que evalúan la accesibilidad individual para cada nodo (García, 1979). El NS indica la mayor distancia topológica que hay partiendo de cada uno de los nodos. Dicho valor corresponde al diámetro de la red. El índice de Shimbel es el número total de arcos necesarios para recorrer desde un nodo a los demás por el tramo más corto. Los nodos con valores de índice Shimbel más bajo corresponden a los nodos más accesibles y centrales, y los valores más altos corresponden a los nodos menos accesibles y ubicados en la periferia de la red. Para su obtención, se debe construir la matriz de conectividad, que es una tabla binaria de doble entrada en la que se consignan el número de arcos y nodos en filas y columnas. De esta matriz se puede conocer la favorabilidad en términos de conexión entre nodos. A partir de ésta, se construye la matriz de accesibilidad topológica, en la que se remplazan los 0 y 1 por las distancias entre nodos de la red, expresada por el número de arcos que se deben recorrer para llegar de un nodo a otro, tomando el camino más corto. Para cada nodo, el valor más alto representa la mayor cantidad de enlaces que necesita recorrer para llegar al nodo más lejano, y el valor más alto de toda la matriz representa los nodos más alejados de toda la red, que equivale también al diámetro de ésta.

Para la visualización espacial de la accesibilidad en 3 dimensiones, Cardozo, et al 2009, utilizan la interpolación de Kernel con barreras. Este método de interpolación brinda la posibilidad de una representación continua a través del uso de funciones y una base raster en la cual cada píxel asume un valor específico de densidad. Este es un indicador de radio de búsqueda que utiliza la distancia más corta entre dos puntos e interpola desde las rutas donde se ubican los datos hasta el lugar donde se requiere una predicción (ArcGis Resource Center, Desktop 10, 2012).

2.2. Selección de sistemas de transporte públicos de bicicletas y adquisición de información

Para la selección de los STPB objeto de estudio, se partió del análisis cuantitativo de las 22 ciudades Latinoamericanas que para el año 2014 contaban con STPB en funcionamiento, al menos en su primera fase. De estas 22 ciudades se seleccionaron las ciudades con sistemas más antiguos, Bike Río (Rio de Janeiro, 2008 y reinaugurado en 2011), Bike Santiago (Santiago de Chile, 2008 y reinaugurado en 2013), Ecobici (México D.F., 2010), Ecobici (Buenos Aires, 2010) y Encicla (Medellín, 2011). Los elementos contemplados para el análisis de red son el año de inicio, infraestructura para bicicletas (número de ciclo estaciones, kilómetros de corredores para bicicletas), número de bicicletas, y total de usuarios desde su apertura hasta finalizar el año 2014. Entre los sistemas de las cinco ciudades seleccionadas se destaca que son los sistemas con mayor número de bicicletas, excluyendo a Sao Paulo, ciudad con el segundo mayor número de bicicletas, pero recientemente puesto en operación (2012) por lo que fue excluido del análisis. Con respecto a la inclusión de Encicla (Medellín), este es de interés por ser uno de los más antiguos y ser el único implementado en Colombia, convirtiéndose en un referente nacional.

El sistema Encicla tiene una red de infraestructura para bicicletas que trata de cubrir la mayor parte de la ciudad de Medellín, concentrándose en la parte plana y dividida en seis zonas. La ciudad de Buenos Aires se caracteriza por sus pendientes muy bajas y el sistema Ecobici ha podido expandir su cobertura a la mayor parte de la ciudad, aunque se identifican los sectores Noreste y Sureste, como los sectores donde se encuentran distribuidas las ciclo estaciones, mientras que, en el sector Oeste hay tramos de red aislados, que no se tuvieron en cuenta por estar desconectados del sistema. El STPB de México D.F. concentra su funcionamiento en zonas céntricas de la ciudad. Dada la uni-direccionalidad de parte de la red, algunos nodos de la zona sur quedan desconectados, siendo posible acceder a una estación como destino, pero no originar viajes desde dicha estación. En este sistema también se encuentran ciclo estaciones independientemente que haya o no presencia de corredores para bicicletas. El STPB Bike Río, nació en la zona de Copacabana en el año 2011, pero ya venían funcionando las bicicletas públicas desde el año 2008, y ha venido extendiéndose por toda la ciudad de Río de Janeiro. La zona este de la ciudad presenta mayor concentración de infraestructura para bicicletas, pero se encuentra distanciada de la infraestructura disponible en la zona oeste; esto como consecuencia de la topografía en la que se asienta la urbe. La ciudad de Santiago de Chile tiene consolidado su STPB Bike Santiago hacia el centro de la ciudad, con algunas infraestructuras para bicicletas que expanden la cobertura en dirección hacia la periferia.

La información que se utilizó para los análisis desarrollados proviene de fuentes secundarias obtenidas a través de la página web oficial de cada sistema y la cartografía base en formato shape para todas las ciudades se obtuvo del portal Geofabrik. La Tabla 1 muestra información sobre las características de cada sistema considerado en el análisis.

Tabla 1
Características de los STPB ciudades latinoamericanas

Fuente: CEPAL, 2008. CAF, 2011. Páginas oficiales de cada sistema, 2015. Alcaldías locales, 2015.

2.3. Diseño de grafos

Los grafos se crearon a partir de la información adquirida de la red de infraestructura para bicicletas correspondiente a cada STPB con la ayuda del Software Grafos - v 1.3.5. de Alejandro Rodríguez Villalobos. Cada sistema se esquematizó en forma de nodos y enlaces, los nodos representados en cuatro tipos (intersección, terminales, ficticios y ciclo estaciones), y los enlaces como las conexiones que comunican cada punto de interés. Con dichas conexiones se obtiene la matriz de conectividad. Esta matriz indica las conexiones existentes entre los nodos y cuantifica este número para cada vértice evaluado. Determina el número de enlaces que parten desde cada nodo para conectarse con otro. A los nodos que tienen conexión se les asigna valor de 1, y a los que no se les asigna valor de 0. Posteriormente con esta matriz se crea la matriz de accesibilidad topológica a través del algoritmo de Floyd-Warshall, evaluando los enlaces que se deben recorrer de nodo a nodo, por el camino mínimo. A partir de ésta información se calcularon los valores de número asociado e índice Shimbel. La construcción de las anteriores matrices proporcionó información importante para el desarrollo de otros indicadores utilizados para el diagnóstico de cada red evaluada. A continuación, la Figura 1 muestra la representación y características de los grafos para cada una de las cinco ciudades latinoamericanas consideradas en el análisis. El color azul hace referencia a las estaciones como parte de la infraestructura para bicicletas, y el color gris a otros nodos como terminales, de intersección y ficticios.

Figura 1
Grafos de los STPB en ciudades latinoamericanas

Fuente: Elaboración propia

Debido a la extensión de las matrices requeridas para el análisis de red en cada uno de los STPB seleccionados, en esta sección se describirán los resultados finales con la correspondiente interpretación para permitir la comparación de dichos sistemas como parte de la evaluación y análisis propuesto. Se presenta la evaluación de los sistemas públicos de bicicletas desde la perspectiva de medidas de conexión, conectividad, accesibilidad y centralidad.

3.1. Medidas de conexión

3.1.1. Estado de la red

(a) Número ciclomático - NC

La ciudad que presenta la red con mayor valor de número ciclomático es Buenos Aires con 36, lo que indica que es la más conectada o compleja, como lo expone Rodrigue et al, 2013. En la medida en que el número de ciclos aumente, la red aumenta también su complejidad. Le siguen Medellín y Santiago de Chile con el mismo número ciclomático, 12. Rio de Janeiro con 10 y finalmente México D.F. con 5, ésta última tiene menos ciclos indicando es una red poco desarrollada. Aunque tiene bastante ciclo estaciones, cuenta con poca infraestructura especializada para el recorrido de los ciclistas únicamente, haciendo que haya menos alternativas de viaje. Figura 2(a).

(b) Índice alfa - IA

Este índice relaciona el porcentaje de circuitos que tiene una red con respecto a los máximos posibles. La red de Buenos Aires tiene un porcentaje alfa de 12,81%, le sigue Medellín con 9,02%, Santiago de Chile con 6,03%, Río de Janeiro con 5,03%. Por último, México con 3,07%. De acuerdo con lo anterior, se puede decir que las redes evaluadas tienen un porcentaje de circuitos muy bajo con respecto a los máximos posibles, indicando que desde esta perspectiva son redes poco desarrolladas (García, 1979). En las redes analizadas se observa que estas tienen poco menos del 10% de los circuitos máximos posibles y se consideran redes con bajo nivel de desarrollo, Figura 2(b).

(c) Índice gamma - IG

Este índice relaciona el porcentaje de arcos que tiene una red con respecto a los máximos posibles. Buenos Aires tiene el 42,08% de todos los arcos posibles. Para estar 100% conectada debería tener 423 arcos, es decir le hacen falta 245 arcos (57,92%). La red de Medellín con un 39,80% de todos los arcos posibles, debería tener 201 arcos para estar 100% conectada, es decir, le faltan 121 arcos (60,20% restante). Santiago de Chile tiene el 37,67% de todos los arcos posibles, haciendo que se posicione en el tercer puesto según el índice gamma. Esta red tiene 113 arcos y le hacen faltan 187 arcos (62,33% restante) para estar 100% conectada. Río de Janeiro ocupa el cuarto puesto con el 37% de todos los arcos posibles. Es una red con 111 arcos y debería tener 300 arcos para estar 100% conectada, le faltan 189 arcos (63% restante). La última posición es para México D.F. que tiene el 35,77% de todos los arcos posibles. Una red con 88 arcos que le hacen falta 158 arcos (64,23% restante) para estar 100% conectada. En las redes analizadas se observan bajos niveles de conexión (menos del 50% en todos los sistemas estudiados), Figura 2(c).

(d) Índice beta - IB

Este índice describe el nivel de complejidad con base en el nivel de conexión. Todas las redes incluidas en el análisis se definen como redes complejas (b > 1) dado sus bajos niveles de conexión y desarrollo. Figura 2(d).

Figura 2
Estado de las Redes de los STPB ciudades latinoamericanas

Fuente: Elaboración propia.

3.1.2. Forma de la red

(a) Grado de cohesión - GC

Se presenta el grado de cohesión de cada ciudad. Para lograr comparar las diferentes ciudades se procede a normalizar entre cero y uno el grado de cohesión. Como resultado de este recalculo se tiene que cuando el grado de cohesión se acerca más a cero significa mayor cohesión y cuando se acerca más a 1, mínima cohesión. Tabla 2.

A nivel general se observa que para todas las ciudades el grado de cohesión está más cercano al límite que indica mínima cohesión. Buenos Aires es la red más conectada, cohesionada o coherente, ofreciendo más alternativas a sus usuarios (Potrykowski y Taylor, 1984). Le siguen en grado de cohesión, Medellín, Santiago de Chile, Río de Janeiro y por último México D.F., que es la red menos conectada y menos coherente de todas, con pocas alternativas de desplazamiento para los usuarios por la falta de corredores para bicicletas uni y bi-direccionales. Figura 3(a).

Tabla 2
Grado de cohesión de los STPB ciudades latinoamericanas

Fuente: Elaboración propia.

(b) Densidad - DS

En la clasificación de mayor densidad de las redes de cada ciudad, se tiene que Buenos Aires es la más densa, el segundo lugar lo ocupa, Medellín, le sigue Santiago de Chile, Río de Janeiro y en el último lugar se ubica México D.F. Buenos Aires, cuenta con la red más densa, porque según Rodrigue, et al 2013, una red es más densa cuando ocupa una buena parte del territorio en términos de enlaces (km) y Superficie en (Km2). Cuanto más alto es el valor, la red está más desarrollada. Figura 3(b).

(c) Indicador de cobertura - IC

El indicador de cobertura evaluado en los STPB, se basa en la longitud total de cada red y el número de nodos existentes en ellas, por lo que el valor de cobertura es el promedio de distancias que se presenta entre nodos, donde a menor distancia promedio mayor cobertura local.

México D.F tiene la red con mayor cobertura, porque presenta el menor promedio de distancia, ya que cuenta con alto número de nodos en comparación a la longitud total de corredores para bicicletas. Seguidamente está Río de Janeiro que tiene una relación similar al caso de México D.F., en cuanto a nodos y longitud de corredores para bicicletas. Le sigue en clasificación de cobertura Medellín y Buenos Aires. Por último, Santiago de Chile presenta menor cobertura, puesto que es una red de gran longitud, y aunque tiene 102 nodos, el promedio de sus distancias es muy alto. Figura 3(c).

3.2. Medidas de accesibilidad

La accesibilidad de las redes de los STPB consideradas en el análisis se encontró partiendo de la matriz de conectividad en la cual los valores de 0 (nodos sin conexión) se reemplazaron por la cantidad de enlaces que es necesario recorrer desde un nodo para llegar a otro por el camino más corto. Para cada nodo, el valor más alto representa la mayor cantidad de enlaces que necesita atravesar para llegar al nodo más lejano, y el valor más alto de toda la matriz representa los nodos más alejados de toda la red, que equivale también al diámetro de ésta.

Figura 3
Forma de las Redes de los STPB ciudades latinoamericanas

Fuente: Elaboración propia.

Las cinco matrices de conectividad estimadas indicaron que la máxima conexión que tienen las redes es 4, a excepción de la red Ecobici de México D.F. que tiene una conexión de 3. Los valores obtenidos indican que los nodos tipo ciclo estaciones poseen un grado de centralidad respecto a nodos adyacentes de manera que prestan un mayor grado de servicio y más oportunidades de transferencia. Los nodos menos conectados en su mayoría son nodos terminales que se ubican en la periferia de la red.

En la matriz de accesibilidad topológica de cada red se observó que el mayor valor fue de 19, 28, 46, 33 y 24, para los sistemas de Medellín, Buenos Aires, México D.F., Río de Janeiro y Santiago de Chile, respectivamente. Estos valores representan el diámetro para cada red, y el par de nodos separados por este número de enlaces corresponde a los nodos menos accesibles.

Las redes de México D.F., Buenos Aires y Santiago de Chile, tienen nodos que no presentan conexiones. Esto ocurre en las líneas unidireccionales a través de las cuales se puede llegar al nodo terminal, pero para salir de él, se deben tomar caminos alternos por vías de uso vehicular motorizado.

3.2.1. Número asociado - NA

Los valores más pequeños en las matrices de accesibilidad topológica de Medellín, Buenos Aires, México D.F., Río de Janeiro y Santiago de Chile son los números asociados (NS) 10, 15, 24, 17 y 13, respectivamente. Dichos valores indican que estos nodos son los más accesibles ya que su distancia topológica hacia el nodo más alejado, es el menor valor que se registra en cada red. Estos nodos están ubicados en la parte central y se recorre menor distancia desde ellos hasta el nodo más distante por el camino mínimo.

En las redes de Buenos Aires y Santiago de Chile, algunos nodos no tienen ninguna conexión, lo que indica que en la matriz de accesibilidad topológica no hay valores de distancias mínimas hacia ningún nodo. En estos casos el valor de NS no puede estimarse y se consideran nodos con accesibilidad limitada. El sistema en México D.F además de presentar esta misma condición para 3 nodos, también presenta 6 nodos que se ubican en líneas unidireccionales, indicando que desde ellos solo se puede atravesar 1 o 2 líneas, por ende, el NS para estos nodos toma estos valores, haciendo que tampoco pueda estimarse un valor de NS que indique su accesibilidad respecto a toda la red. Para estos casos la accesibilidad se denota como limitada.

3.2.2. Índice shimbel - IS

El mayor índice Shimbel según la matriz de accesibilidad topológica de cada red es 823, 2575, 1712, 1935 y 1354, para los sistemas de Medellín, Buenos Aires, México D.F., Río de Janeiro y Santiago de Chile, respectivamente. Los nodos representados por estos valores son los nodos más alejados de toda la red. Para llegar desde estos, al resto de nodos, se debe pasar por el mayor número de líneas. En algunos casos, varios nodos tienen igual valor de NS, por lo tanto, el de menor accesibilidad es el que posee el índice Shimbel más alto (Cardozo, 2009).

De igual manera, el menor índice Shimbel es 350, 1037, 842, 874 y 618 para los sistemas de Medellín, Buenos Aires, México D.F., Río de Janeiro y Santiago de Chile, respectivamente, indica que los nodos representados por éstos valores poseen el menor número de arcos para llegar al resto de nodos de cada red. Estos son los nodos más accesibles de la red y se encuentran en el centro de la misma. Como pasó con el NS, en las redes de Buenos Aires, México D.F. y Santiago de Chile, algunos nodos no tienen ninguna conexión, o se ubican en líneas unidireccionales, lo que indica que en la matriz de accesibilidad topológica no hay valores de distancias mínimas hacia ningún nodo, o hay valores para 1 o 2 nodos solamente, por lo que el valor del índice Shimbel tampoco puede estimarse, y para estos casos la accesibilidad está limitada, como se explicó anteriormente.

3.3. Síntesis de resultados

Con el propósito de efectuar un análisis comparativo de los criterios evaluados en cada STPB, se presenta en la Figura 4 gráficas tipo radial con los criterios normalizados, de las cuales se identifica mayores áreas representan criterios más favorables en términos de conexión, centralidad y accesibilidad.  En la Figura 4 se observa condiciones más favorables para el STPB de la ciudad de Medellín, seguido por Buenos Aires, Santiago de Chile, Río de Janeiro y México D.F.

Adicionalmente, los STPB se han representado a través de la interpolación Kernel y la visualización en 3D se presenta en la Figura 5, el color verde indica una condición de accesibilidad más favorable y el color rojo una condición de accesibilidad menos favorable.

Figura 4
Síntesis indicadores evaluados para los STPB ciudades latino

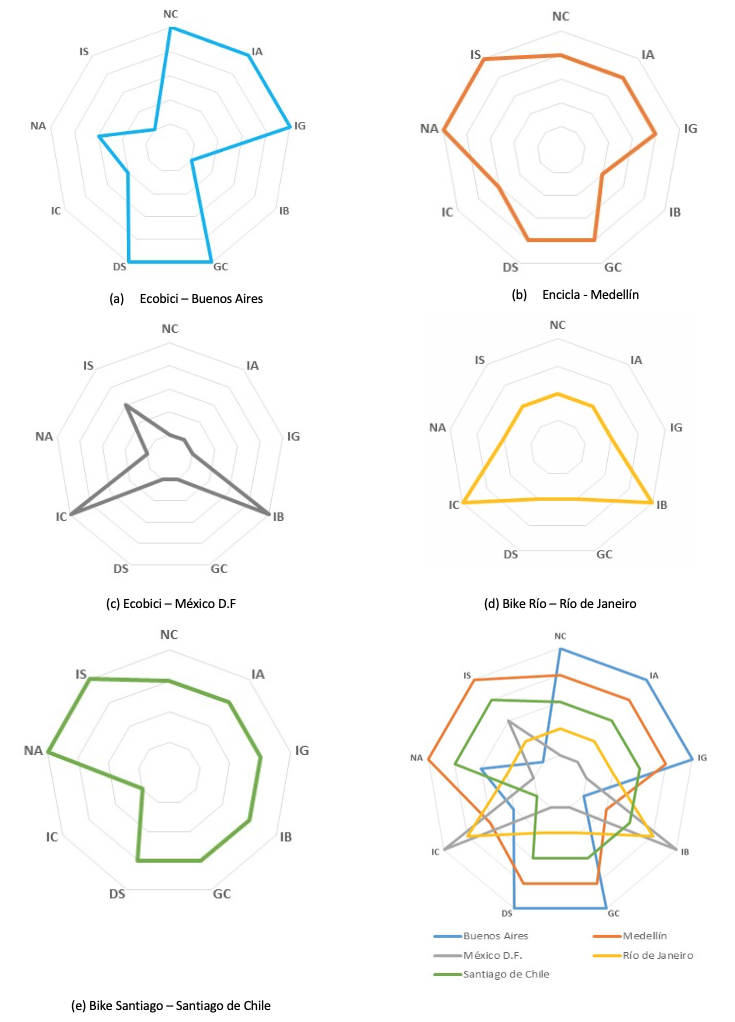
NC: número ciclomático. IA: índice alfa. IG: índice gamma. IB: índice beta.
GC: grado de cohesión.  DS: densidad. IC: índice de cobertura.
NA: número asociado. IS: índice shimbel americanas
Fuente: Elaboración propia

Figura 5
Accesibilidad (Interpolación Kernel) para los STPB ciudades latinoamericanas

Fuente: Elaboración propia.

El presente estudio fue de carácter exploratorio dado que no existen investigaciones anteriores que hayan evaluado la red de infraestructura de un sistema de transporte público de bicicletas utilizando la teoría de grafos; por tal razón, se tomó como referente para discutir los resultados, estudios hechos por autores en redes de metro, subway y redes de transporte público motorizado.

La relación de arcos y nodos hace que se tenga una visión de la red estudiada en cuanto a su extensión. Se podría pensar que en la medida que ésta sea más grande el grado de complejidad o conectividad es mayor. Sin embargo, de acuerdo a las comparaciones efectuadas se encontró que no siempre el tamaño es un indicador de desarrollo, por lo tanto, es importante ver la manera en que éstas se encuentren distribuidas y enlazadas.

Al evaluar el grado de complejidad de la red (medidas de conexión) los resultados coinciden que la red más conectada y desarrollada es la de Buenos Aires y la menos compleja es la de México D.F, indicando que los valores de los indicadores son acertados para realizar el diagnóstico de manera confiable. El STPB Ecobici de México D.F., concentra un alto número de ciclo-estaciones en el centro de la ciudad, y al no tener en cuenta su ubicación con la presencia de corredores para bicicletas, que a su vez no están planificadas de acuerdo al comportamiento vial de la ciudad, hace que los usuarios no tengan alternativas de movilidad dentro de la red de infraestructura para bicicletas, por lo que se ven obligados a transitar por las vías de uso exclusivo para vehículos.

Lo anterior también se ve sustentando con el indicador de cohesión, que da como resultado que todas las redes presentan un nivel bajo de coherencia, ya que su valor se acerca más al límite que indica menor grado de coherencia. Dado que los STPB aún no se están planificando con la misma importancia que se hace con otro medio de transporte, sería necesario implementar nuevas conexiones que generen diversas alternativas entre lugares de mayor importancia en las ciudades.

Respecto a la representación de los mapas de accesibilidad, se observa cómo los valores más pequeños de Shimbel se agrupan en la zona central de cada red, y los menos accesibles se distribuyen hacia la periferia debido a que entre más central se encuentre el nodo, menos distancias se debe recorrer para comunicarse con el resto de nodos. Lo anterior se pudo notar en la vista en 3D de la interpolación de Kernel, en la que se observa cómo en las zonas más altas, el sistema es más asequible para los usuarios, debido a la centralidad que representan respecto a toda la red.

Alcaldía de Buenos Aires. (2015). http://www.buenosaires.gob.ar

Alcaldía de Medellín. (2015). https://www.medellin.gov.co

Alcaldía de México D.F. (2015). http://www.df.gob.mx

ArcGis Resource Center, Desktop 10; 2012, ArcGis Geographic Information System.

Alcaldía de Santiago de Chile. (2015). http://www.municipalidaddesantiago.cl

BIKE RÍO. (2015). http://www.mobilicidade.com.br/bikerio.asp

BIKE SANTIAGO. (2015). http://www.bikesantiago.cl

Banco de Desarrollo de América Latina, CAF. (2011). Desarrollo Urbano y Movilidad en América Latina.

Cardozo, D., Gómez, E. L., y Parras, M. A. (2009). Teoría de Grafos y Sistemas de Información Geográfica aplicados al Transporte Público de Pasajeros en Resistencia (Argentina). Revista Transporte y Territorio, 1, 89-111.

Clean Air Institute. (2012). Revisión de los Sistemas de Bicicletas Públicas para América Latina: Beneficios y Obstáculos. Documento de política. Pardo, C.

Derrible, S., Kennedy, C. (2010). Network Analysis of World Subway Systems Using Updated Graph Theory. Transportation Research Record: Journal of the Transportation Research Board, 2112, 17-25.

Derrible, S., y Kennedy, C. (2010). The complexity and robustness of metro networks. Physica A: Statistical Mechanics and its Applications, 389(17), 3678-3691.

ECOBICI. (2015). http://www.buenosaires.gob.ar/ecobici

ECOBICI. (2015). https://www.ecobici.df.gob.mx

ENCICLA. (2015). http://encicla.gov.co

García, A. (1979). La red de transportes de la provincia de Almeria: Aplicación metodológica de la Teoría de Grafos. p. 137-152.

Geofabrik (2015). https://www.geofabrik.de

Instituto de Informática Universidade Federal do Rio Grande do Sul. (2010). Análise da Complexidade do Algoritmo de Floyd-Warshall. García, C., y Pires, C.

Institute for Transportation and Development Policy. (2012). Planes Integrales de Movilidad. Medina y Veloz.

Institute for Transportation and Development Policy. (2010). Experiencias y lecciones de sistemas de transporte público en bicicleta para América Latina. Pardo, C., Calderón, P., Baranda, B., Medina, C., y Treviño, X.

Kansky, K. J. (1963). Structure of transportation networks: relationships between network geometry and regional characteristic. Chicago: University of Chicago.

Potrykowski , M., y Taylor, Z. (1984). Geografía del Transporte. Barcelona: Ariel.

Prefeitura de Río de Janeiro. (2015). http://www.rio.rj.gov.br

Rodriguez, J. P., Comtois, C., y Slack, B. (2013). The Geography of Transport Systems. New York: Taylor & Francis.

Taczanowska, K., González, L. M., Garcia-Massó, X., Muhar, A., Brandenburg, C., y Toca-Herrera, J. L. (2014). Evaluating the structure and use of hiking trails in recreational areas using a mixed GPS tracking and graph theory approach. Applied Geography, 55, 184-192.

1. Ingeniero Topográfico. Universidad del Valle. iguillobravox@gmail.com

2. Ingeniera Topográfica. Universidad del Valle. angela.rojas14@hotmail.com

3. Ph.D en Ingeniería de Transporte. Profesor Asociado Escuela de Ingeniería Civil y Geomática. Universidad del Valle. ciro.jaramillo@correounivalle.edu.co

4. Ph.D en Ingeniería Civil. Profesor Asistente Escuela de Ingeniería Civil y Geomática. Universidad del Valle. jackeline.murillo@correounivalle.edu.co