

Vol. 39 (Nº 50) Año 2018. Pág. 6
Daniel Felipe ESCOBAR Morales 1; Juan Esteban GAVIRIA Cano 2; Juan Pablo OREJUELA Cabrera 3
Recibido: 21/06/2018 • Aprobado: 30/08/2018 • Publicado 15/12/2018
RESUMEN: Se propone un método de solución a problemas de ruteo de buses escolares, desarrollado en tres fases: caracterización de datos, asignación de niños a vehículos y creación de rutas. Se usan técnicas heurísticas o/y exactas para cada sub problema. Se propone una extensión al modelo de Asignación Generalizada de Fisher y Jaikumar en la que se considera que los grupos a formar tienen capacidad heterogénea. El método es integral, validado mediante caso de estudio y aplicado a diferentes escenarios. |
ABSTRACT: A method of solving school bus routing problems is proposed, it is developed in three phases: data characterization, assignment of children to vehicles and routing. heuristic or / and exact techniques are used for each sub problem. An extension to the Fisher and Jaikumar Generalized Assignment model is proposed. in this it is considered that the groups to be formed have heterogeneous capacity. The method is integral, validated in a case study and applied to different scenarios. |
Los Problemas de Ruteo de Buses Escolares hacen parte de la familia del VRP (Kinable, Spieksma, & Vanden, 2014), los cuales se caracterizan por estar compuestos de tres principales sub-problemas: la asignación de paradas a los buses, la asignación de los estudiantes a los buses y, por último, la selección de la ruta de cada bus. Estos problemas de enrutamiento de vehículos son de tipo NP-Hard (Fügenschuh, 2007) (Park & Kim, 2010) (Rocha, González & Orejuela, 2011) (Kinable, Spieksma & Vanden, 2014).
Denominado como SBRP (School Bus Routing Problem), este problema también se fundamenta en casos del TSP (Traveling Salesman problema), con múltiples agentes viajeros. Las variables aplicadas a los problemas del TSP, como rutas, cantidad de vehículos o combinaciones de ambos, son factibles para el SBRP.
La complejidad del TSP y del VRP no sólo se limita a la cantidad exponencial de posibles soluciones, sino también a las restricciones propias de cada tipo de problema. Por ejemplo, el VRP cuentan cerca de 36 tipos de problemas (Rocha, González & Orejuela, 2011). El tiempo y modos de cálculo para resolverlos los catalogan como problemas Np-Hard.
El Problema del Ruteo de Buses Escolares (SBRP), busca la definición de un plan para programar buses que deben recoger estudiantes en paradas o en casas específicas, para llevarlos a la escuela, teniendo en cuenta limitaciones como la capacidad máxima del bus, el tiempo máximo de permanencia de los estudiantes en el bus y ventanas de tiempo de la escuela (Yigit & Unsal, 2016). Este problema ha gozado del interés de los investigadores y muchos coinciden en la importancia de abordarlo como parte importante del transporte público (Kelly & Fu, 2014; Nasrudin & Nor, 2013; Park & Kim, 2010).
Una de las particularidades del SBRP frente a otros problemas de ruteo de vehículos, es involucrar elementos propios del transporte de pasajeros (Araya, Obreque, & Paredes, 2012; Kim, Kim, & Park, 2012; Park & Kim, 2010). Aspectos como la comodidad, la rapidez, la seguridad y el bienestar de los pasajeros cobra importancia en la búsqueda de una solución que considere la normatividad del transporte de pasajeros (Ibrahim, Adji, & Karim, 2013).
El SBRP, como estructura genérica, se puede descomponer en cinco subproblemas: la preparación de datos, selección de paradas de autobús, generación de rutas, ajuste con el timbre de la escuela y programación de buses (Desrosiers, Ferland, Rousseau, Lapalme, & Chapleau, 1981). Esta descomposición busca reducir la complejidad, de tal modo que los subproblemas pueden ser solucionados por separado facilitando la solución del problema global (Park & Kim, 2010).
El presente artículo pretende, ante la complejidad que pueden presentar los problemas del ruteo de buses es colares, un modelo hibrido que divide los sub-problemas del SBRP de manera que para hallar una solución puedan operar más de una técnica metodológica. Se hace una descripción y una aplicación, en la que el modelo propuesto se valida en un caso de estudio. Este modelo híbrido pretende así ahondar dentro de las posibilidades metodológicas e investigativas dentro de los SBRP y el desarrollo de sus soluciones.
Dado la complejidad que pueda presentar una técnica para solucionar un SBRP de manera global, es necesario el uso de métodos que utilice más de una estrategia para resolver los diferentes sub-problemas antes descritos. El método de solución que propone este artículo para al Problema de Ruteo de Buses Escolares se desarrolla en 3 partes enfocadas a los siguientes tres sub-problemas: la asignación de paradas a los buses, la asignación de los estudiantes a los buses y la selección de la ruta de cada bus. De esta forma se abordan metodologías heurísticas y metaheurísticas dependiendo de la complejidad, tipo de problema y variable presente en la aplicación. A continuación, se representa el modelo propuesto, seguido de una explicación detallada de las diferentes fases:
Gráfica 1
Diagrama de flujo con modelo de 3 fases propuesto

Se aborda el primero de los sub-problemas: La preparación de datos, esta se divide en dos componentes: caracterización del SBRP y matriz de distancias. Para cada uno de los dos componentes se seleccionan técnicas de solución adecuada para obtener la información necesaria para el desarrollo de los sub-problemas siguientes. La obtención de datos es primordial para desarrollar un tratamiento eficaz a los problemas del SBRP, estos determinan las variables y mejoran el panorama del problema.
Para este componente de la Fase I se cuenta con herramienta de caracterización sobre los criterios más utilizados en trabajos relacionados con el ruteo de Buses Escolares esta se puede ver en (Park & Kim, 2010).
Para hallar la matriz de distancias, en la mayoría de casos, se usan sistemas de información geográfica. El proceso descrito a continuación es útil cuando el problema tiene en cuenta un gran número de nodos en la que se tiene información concreta de direcciones:
Paso 1. Modificar el formato de los datos de ubicación para cumplir con el siguiente estándar: CALLE/CARRERA/AVENIDA x # x – x Ciudad, País.
Paso 2. Obtener a partir de las herramientas de Google® y Google Earth®. Las coordenadas geográficas (HH;MM;SS – Grados, Minutos y Segundos) de cada uno de las direcciones.
Paso 4. Convertir las coordenadas geográficas a coordenadas planas (metros norte, metros estos).
Paso 5. Construir la matriz de distancias euclidianas.
La asignación de estudiantes a buses establece el número de estudiantes que serán recogidos por cada bus, teniendo en cuenta la capacidad de cada uno automotor. En esta investigación Se utilizan dos estrategias para la asignación de estudiantes: La primera estrategia es una heurística conocida como barrido o sweep y la segunda estrategia se basa en la modelación matemática basada en la Asignación Generalizada de Fisher y Jaikumar (Olivera, 2004).
La heurística de barrido inicia con la formación de un clúster, girado una semirrecta con origen en el depósito, incorpora a los clientes “barridos” por dicha semirrecta hasta que se cumplan restricciones de capacidad. El algoritmo es aplicado en problemas planos, donde cada nodo i puede ser representado en un plano cartesiano ya sea con coordenadas polares (pi, θi) o coordenadas cartesianas (Xi, Yi). Las distancias entre todos los puntos se asumen que son euclidianas:
Paso 1. Empezar la rotación en semirrecta, barriendo a cada uno de los estudiantes i para ingresarlo a un clúster k. Si dos estudiantes tienen igual valor de θ, se coloca primero el de menor valor p.
Paso 2. Si todos los estudiantes pertenecen a un mismo clúster seguir con el paso 3, sino realizar el Paso 1 hasta el límite de capacidad del clúster k, si aún faltan estudiantes por agrupar, se crea un nuevo clúster y se vuelve al paso 1.
Paso 3. Realizar el procedimiento en varias ocasiones, cambiando el punto de inicio de giro de la semirrecta, con el fin de obtener diferentes agrupaciones de clientes.
Una de las restricciones que tiene el modelo de Asignación Generalizada de Fisher y Jaikumar (Olivera, 2004), es su capacidad, asume que todos los grupos a formar poseen la misma distribución. Por lo tanto, en la presente investigación se propone una extensión al modelo de Asignación Generalizada de Fisher y Jaikumar en la que se considera que grupos a formar tienen capacidad heterogénea.

Se realiza la respectiva generación de rutas para cada bus bajo la asignación de estudiantes adecuada. La intención de fragmentar el Problema de Ruteo de Buses Escolares es simplificar el problema de ruteo al punto de tener la sumatoria de varios TSP. Al igual que en la Fase anterior, se propone inicialmente un método exacto para obtener una solución óptima de TSP.
Se usa un modelo matemático generalizado para la solución del TSP (Cordeau, Laporte, Savelsbergh & Vigo, 2007) (Olivera, 2004) (Toth & Vigo, 2002).

Considerado como NP-Hard, por su cantidad exponencial de posibles soluciones, el problema de ruteo puede llegar a dimensiones dentro de las cuales el método exacto propuesto no es suficiente, por lo cual se recurre a otras técnicas de solución. En estas es necesaria la utilización de herramientas alternativas como el Concorde TSP, una herramienta gratuita en internet para resolver problemas de optimización numérica ofrecida por el Instituto de Investigación de la Universidad de Wisconsin en Madison. Usa un código de computadora para solucionar el Problema del Agente Viajero y algunos problemas de optimización de redes similares.
Aplicamos el método propuesto para encontrar solución al problema de SBRP propuesto dentro de un caso de estudio que servirá para validar la eficacia del mismo. Se desarrollarán las fases propuestas por el método y se especificará el uso de las mismas durante su desarrollo. Se opta por un caso de estudio en el que las rutas del colegio infantil son coordinadas por una empresa de transporte externa, la cual se encarga de proveer el servicio de transporte a los 170 estudiantes que deben asistir a clase todos los días. La compañía coordina el orden de recogida de los niños de forma intuitiva en términos de cercanía de un punto a otro. Es importante resaltar que actualmente no se tiene control acerca de la distancia recorrida, ni la variabilidad del tiempo que puede presentar. Con lo cual, contamos con un caso de estudio que presenta problemas de logística que requieren de la intervención de un modelo capaz de proponer objetivos claros de eficiencia y modelos de transporte efectivos y coordinados. La compañía coordinadora de transporte para cumplir con el traslado de estos niños emplea un total de 11 vehículos cuyas especificaciones se muestran a continuación:
Tabla 1
Flota de vehículos caso estudio
KIA Pregio - 2006 |
Nissan Urban - 2013 |
Chevrolet NKR - 2003 |
Cantidad: 1 |
Cantidad: 2 |
Cantidad: 1 |
Capacidad: 17 |
Capacidad: 15 |
Capacidad: 16 |
Nissan Urban - 1992 |
Citroen Jumper - 2009 |
KIA Pregio - 2005 |
Cantidad: 1 |
Cantidad: 1 |
Cantidad: 2 |
Capacidad: 16 |
Capacidad: 19 |
Capacidad: 14 |
DFM - 2014 |
KIA Pregio - 2008 |
Nissan Urban - 2014 |
Cantidad: 1 |
Cantidad: 1 |
Cantidad: 1 |
Capacidad: 10 |
Capacidad: 16 |
Capacidad: 18 |
Fuente: Autores.
En el desarrollo de la Fase I del modelo propuesto se propone como entregable de este punto la caracterización del problema de acuerdo con las principales particularidades de un SBRP y principalmente la matriz de distancias entre todos los nodos: estudiantes y colegio (tabla 2).
Tabla 2
Caracterización del modelo
Criterio |
Consideración |
Número de Colegios |
Un Colegio |
Tipo de servicio |
Urbano |
Jornada estudiantil |
Mañana (Recoger estudiantes) |
Recogidas combinadas |
No aplica |
Estudiantes especiales |
Estudiantes en general |
Tipo de flota |
Flota heterogénea |
Objetivo |
Tiempo o distancia total en el viaje de los buses |
Constantes |
Capacidad de buses |
Fuente: Autores.
De acuerdo a la caracterización del problema se cumple con las restricciones y la finalidad del modelo descritas anteriormente. El número de estudiantes plantea una dificultad para hallar una solución, ya que en el desarrollo de la segunda y tercera fase se identifique un problema NP-Hard. Haciendo insuficiente el uso de métodos exactos para resolver el problema, sin mencionar el reto que se dispone al hallar la matriz de distancias por la cantidad de estudiantes.
La matriz de distancias, en el caso estudio, cuentan con 170 estudiantes más 1 colegio. Se calcula una matriz de 171x171. Se muestra la ubicación geográfica de cada uno de los estudiantes en el mapa de Cali con la ayuda del software Google Earth®. Los estudiantes están enumerados del 2 al 171, y el número 1 hace referencia al Colegio.
Gráfica 2
Ubicación geográfica de los estudiantes en el mapa de Cali - Google Earth
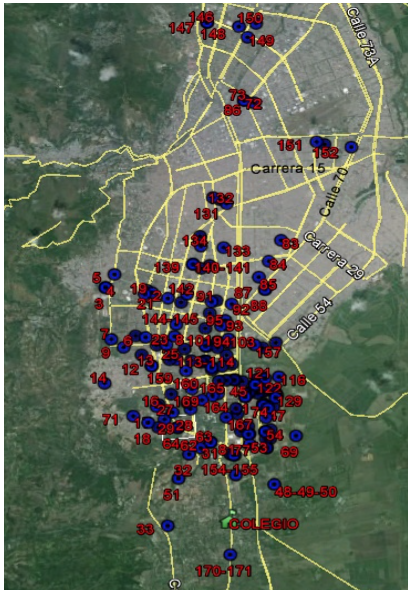
Se define en primera instancia si la flota es homogénea o heterogénea, depende de esto la utilización de un modelo matemático adecuado. Se concluye que, en revisión al caso de estudio, la flota está compuesta por 11 buses de capacidades diferentes: flota heterogénea.
El número de estudiantes a asignar N es de 170, el número de clúster a formar M es de 11 (ya que se cuenta con 11 buses en el caso estudio) y las capacidades de estudiantes Kc son; 19, 18, 17, 16, 16, 16, 15, 15, 14, 14 y 10 para cada bus respectivamente.
De acuerdo con el método planteado, cuando no se encuentra una solución óptima con el modelo matemático se selecciona el uso de la heurística del barrido, la cual se lleva a cabo del barrido o sweep sobre el mapa obtenido en la matriz de distancia (Gráfica 2). Después de probar diferentes puntos de partida se toma como punto de partida de la semirrecta el punto cardinal sur en dirección de las manecillas del reloj. Con lo cual se obtienen los siguientes resultados de agrupación:
Tabla 3
Agrupación de estudiantes - Escenario 1, Semirrecta Sur
Capacidad del bus |
Bus 1 |
Bus 2 |
Bus 3 |
Bus 4 |
Bus 5 |
Bus 6 |
Bus 7 |
Bus 8 |
Bus 9 |
Bus 10 |
Bus 11 |
1 |
E170 |
E12 |
E144 |
E113 |
E101 |
E148 |
E85 |
E76 |
E40 |
E38 |
E127 |
2 |
E171 |
E13 |
E145 |
E114 |
E112 |
E92 |
E87 |
E77 |
E41 |
E75 |
E129 |
3 |
E33 |
E3 |
E159 |
E138 |
E146 |
E167 |
E88 |
E78 |
E42 |
E74 |
E59 |
4 |
E51 |
E4 |
E143 |
E161 |
E147 |
E95 |
E157 |
E79 |
E43 |
E57 |
E60 |
5 |
E71 |
E6 |
E164 |
E169 |
E131 |
E149 |
E84 |
E153 |
E152 |
E53 |
E61 |
6 |
E18 |
E30 |
E102 |
E106 |
E82 |
E110 |
E36 |
E73 |
E119 |
E39 |
E68 |
7 |
E32 |
E28 |
E142 |
E105 |
E132 |
E150 |
E37 |
E45 |
E72 |
E70 |
E69 |
8 |
E8 |
E23 |
E158 |
E96 |
E130 |
E166 |
E86 |
E46 |
E116 |
E64 |
E48 |
9 |
E5 |
E20 |
E140 |
E91 |
E136 |
E97 |
E83 |
E35 |
E118 |
E65 |
E49 |
10 |
E16 |
E22 |
E141 |
E165 |
E137 |
E168 |
E47 |
E121 |
E125 |
E58 |
E50 |
11 |
E7 |
E24 |
E154 |
E162 |
E133 |
E117 |
E156 |
E89 |
E66 |
E55 |
- |
12 |
E31 |
E27 |
E155 |
E134 |
E104 |
E111 |
E120 |
E126 |
E128 |
E56 |
- |
13 |
E9 |
E2 |
E139 |
E98 |
E163 |
E80 |
E115 |
E122 |
E62 |
E52 |
- |
14 |
E15 |
E19 |
E107 |
E99 |
E94 |
E44 |
E151 |
E123 |
E63 |
E54 |
- |
15 |
E14 |
E26 |
E108 |
E100 |
E93 |
E81 |
E34 |
E124 |
- |
- |
- |
16 |
E17 |
E25 |
E109 |
E90 |
E103 |
E67 |
- |
- |
- |
- |
- |
17 |
E29 |
E21 |
E135 |
- |
- |
- |
- |
- |
- |
- |
- |
18 |
E10 |
E160 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
19 |
E11 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
Fuente: Autores.
Cada uno de los números asignados a los buses corresponde a los números respectivos de cada estudiante (Gráfica 2). La tabla 3 resume el entregable principal de la segunda fase el modelo propuesto, aquí se asignan todos los estudiantes a cada uno de los buses sin exceder la capacidad máxima de los mismos.
De la fase anterior obtenemos datos precisos de los estudiantes que deben ser recogidos por cada uno de los buses disponibles. Se define en esta fase la generación de 11 buses para recoger a los estudiantes asignados, se convierte el problema de ruteo en un TSP para cada bus.
Tal como lo indica el método propuesto de solución, se debe utilizar el modelo para rutear mediante la modelación matemática del TSP, donde N es el número de estudiantes a recoger por cada uno de los buses y dij son las distancias entre dichos estudiantes obtenidas de la matriz de distancias, resultado del desarrollo de la Fase I del método. Para la solución se utiliza MINTO. Se obtuvo las siguientes rutas de cada uno de los buses:
Tabla 4
Resultados obtenidos mediante modelo matemático
Número de Bus |
Solución óptima (Total recorrido de ruta) |
9 |
24.769 |
10 |
8.662 |
11 |
9.494 |
Fuente: Autores.
El modelo matemático encuentra solución óptima para los buses 9, 10 y 11, pero para los buses del 1 al 8 no se encuentra resultado, esto se debe a que el tamaño del problema excede la capacidad del modelo matemático, es decir que el tiempo computacional necesario excede a la capacidad ofrecida por MINTO de 4 horas. La razón por la que ocurre esto, es porque el número de posibles soluciones crece de manera exponencial según el número de estudiantes, en este caso se puede definir que el modelo matemático solo resuelve hasta un límite de 15 nodos, 14 estudiantes y el colegio.
El uso de Concorde-TSP se realiza mediante la plataforma ofrecida por Neos Solver. Se procede entonces a realizar la generación de las rutas para los buses del 1 al 8 con la herramienta Concorde-TSP obteniendo los siguientes resultados:
Tabla 5
Resultados obtenidos mediante herramienta Concorde – TSP (Rutas 1 – 8)
Número de Bus |
Solución (Total recorrido de ruta) |
1 |
17.455 |
2 |
16.555 |
3 |
20.874 |
4 |
17.125 |
5 |
31.686 |
6 |
32.385 |
7 |
24.807 |
8 |
24.628 |
Fuente: Autores
Al final de la aplicación del método, teniendo en cuenta los supuestos y restricciones del modelo, obtenemos una solución que minimiza el recorrido total; tiempo de recorrido y permanencia de los estudiantes en ruta, a un valor de 228.440.
En el desarrollo del método propuesto, existen dos momentos en los cuales, dependiendo del tamaño del problema, se utilizan técnicas de modelación matemática o las respectivas alternativas. La Fase III, buscará disminuir la distancia total recorrida por cada ruta y la razón por la cual los resultados de estos ruteos se ven afectados es por la asignación de los estudiantes a cada uno de los buses, resultado de la Fase II, por lo tanto, se identifica como variable que afecta directamente el resultado global del método propuesto. La técnica de heurística del barrido es usada, debido a la dimensión del problema el método exacto no es suficiente para encontrar una solución óptima.
Al utilizar la heurística de barrido, las agrupaciones realizadas para cada uno de los estudiantes son determinadas por la posición inicial, de donde se extiende la semirrecta que “barre” a cada uno de los puntos en el plano cartesiano. A continuación, se presentan los resultados para tres diferentes puntos de inicio:
Tabla 6
Resultados - Análisis de sensibilidad escenarios 1 y 2
Norte |
Sur |
Occidente |
|
Distancia total recorrida |
234.259 |
228.440 |
233.846 |
Promedio de distancias recorridas por bus |
21.296 |
20.767 |
21.259 |
Recorrido máximo |
31.891 |
32.470 |
32.385 |
Recorrido mínimo |
9.554 |
8.662 |
8.982 |
Fuente: Autores.
Tal como se ven en los resultados de cada uno de los escenarios para la heurística de barrido, la posición inicial de la semirrecta al momento de realizar la agrupación por el método del barrido afecta directamente el resultado final del método de solución, como se puede observar el primer escenario es quien arroja un mejor resultado final al tener la menor distancia total recorrida, presenta un incremento del 2,5 % con respecto a la primera instancia planteada, y el segundo escenario presenta una mejora del 0,2 % respecto a la primera instancia. Para los escenarios 3, 4 y 5 los resultados se establecen en la Tabla 7.
Para este análisis de sensibilidad se supone una flota homogénea de buses, con el fin de utilizar el modelo matemático de Asignación generalizada de Fisher y Jaikumar y analizar cómo afecta la asignación en el resultado global del método. Para realizar el análisis con flota homogénea se busca capacidades de buses las cuales cumplan con la condición de asignar los 170 estudiantes exactamente, las capacidades que cumplen con estas condiciones son buses con capacidad para; 5, 10, 17 y 34 estudiantes:
Tabla 7
Resultados - Análisis de sensibilidad escenario 3, 4 y 5
Homogénea 5 |
Homogénea 10 |
Homogénea 17 |
Homogénea 34 |
|
Distancia total recorrida |
412.454 |
231.908 |
163.470 |
104.560 |
Promedio de distancias recorridas por bus |
12.131 |
13.642 |
16.347 |
20.912 |
Recorrido máximo |
33.197 |
35.031 |
36.244 |
39.320 |
Recorrido mínimo |
5.594 |
6.413 |
10.495 |
12.758 |
Fuente: Autores.
Para realizar el análisis del efecto que tiene la capacidad de los buses (en el caso de tener flota homogénea) en el resultado del método de solución propuesto se presentan los siguientes gráficos:
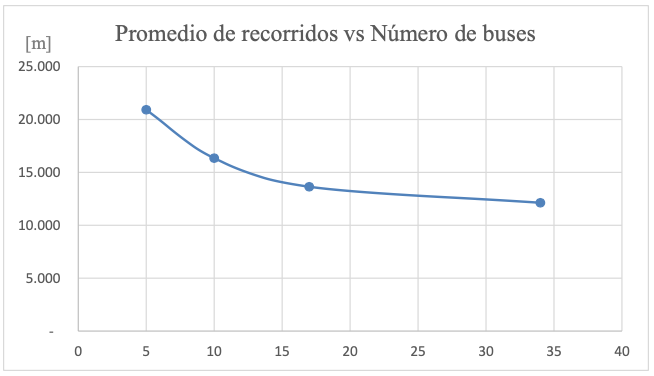
Gráfica 3
Promedio de recorridos de los Escenarios 3, 4 y 5. Fuente, el autor.
-----
Gráfica 4
Distancia total recorrida de los Escenarios 3, 4 y 5.

Fuente, el autor
Tal como se observa en los gráficos presentados, al aumentar el número de buses la distancia total recorrida también aumenta con una tendencia lineal, esto se debe a que cada bus adicional implica un recorrido adicional entre el primer niño y el colegio, es decir se aumentan el número de recorridos de ida y vuelta al colegio, lo cual impacta negativamente la función de desempeño de disminuir la distancia total recorrida.
Por el contrario, a mayor número de buses menor es la distancia promedio de los recorridos, la cual presenta una tendencia exponencial negativa, es decir que se llegará a un punto en el cual, por más buses que se introduzcan en el sistema, este no presentara diminuciones significativas en el promedio de distancias de los recorridos. Esta disminución del promedio de recorridos al aumentar el número de buses se debe a que, si se tienen más buses para atender los estudiantes, el primer estudiante recogido por el bus “x”, permanecerá menos tiempo en la ruta, ya que hay menos estudiantes que recoger por el mismo bus “x”.
El aumento de número de buses llegará a tal punto que la distancia promedio recorrida es el promedio de las distancias de los estudiantes al colegio, con lo cual se evidencia que por más buses que existan en el sistema, la distancia promedio de recorridos no disminuirá más (gráfica 2).
Si comparamos los escenarios 1 y 2 (flota heterogénea) con los escenarios 3, 4 y 5 (flota homogénea), se puede evidenciar que la flota homogénea tiende a arrojar mejores resultados tanto en recorrido total como en recorrido promedio por las rutas tal como se observa en la siguiente tabla:
Tabla 8
Resultados sensibilidad flota heterogénea vs flota homogénea
Flota heterogénea |
Flota homogénea |
|
Distancia total recorrida |
232.182 |
228.098 |
Promedio de distancias recorridas por bus |
21.107 |
15.758 |
Recorrido máximo |
32.249 |
35.948 |
Recorrido mínimo |
9.066 |
8.815 |
Fuente: Autores.
El mejoramiento de la distancia total recorrida utilizando flota homogénea es de 1,76 %, mientras que el mejoramiento en cuanto a promedio de distancias recorridas es de 25,34 %. Sin embargo, el recorrido máximo con la menor distancia registrada se encuentra con Flota heterogénea.
Los problemas relacionados con el OVR, como lo son el SBRP, en la actualidad son problemas de necesaria intervención por parte de entidades gubernamentales y privadas para mejorar la eficacia de los servicios y la movilidad urbana. El Método propuesto de tres fases para la solución del SBRP se entiende como un método que explora diferentes técnicas, heurísticas y exactas, para encontrar una solución. La subdivisión del problema del SBRP y la posibilidad de usar diferentes técnicas de resolución en cada una de estas provee la capacidad para hallar la solución más eficaz dentro de una gama de posibilidades.
Durante la validación de nuestro modelo, aludiendo a diferentes escenarios dentro de un caso de estudio, destacamos cómo las soluciones, a pesar de su complejidad, pueden ser encontradas a través de técnicas distintas. Ya que un mismo subproblema, pero que compromete variables distintas, puede no responder de la misma manera a técnicas de solución generalizada. Por esta razón, y por la diversidad y pluralidad de técnicas usadas para hallar una solución del SBRP, define al método propuesto en el presente artículo como un método integral y eficaz para abordar el problema de ruteo de buses escolares.
Brindar la posibilidad de usar técnicas distintas hace que, sin importar la ciudad, o las variables que presenten estos problemas, hallar una solución eficiente sea factible. Con lo que se crea una metodología, que plantea una actualización de otras técnicas, y la reflexión sobre la necesidad de explorar métodos de solución no generalizados o que aborden el problema como uno sólo y que reduzcan la posibilidad de encontrar soluciones que dentro de los problemas relacionados con el SBRP.
Araya, N., Obreque, C., & Paredes, G. (2012). Un Modelo De Programación Lineal Entera Mixta Para El Problema De Ruteo De Vehiculos Del Transporte Escolar. In Simposio Brasileiro de Pesquisa Operacional (pp. 2293–2302).
Cordeau, J., Laporte, G., Savelsbergh, M., & Vigo, D. (2007). Vehicle Routing. Handbook in OR & MS, 14.
Desrosiers, J., Ferland, J., Rousseau, J., Lapalme, G., & Chapleau, L. (1981). An overview of school busing system. Scientific Management of Transport Systems, 235-243.
Fügenschuh, A. (2007). Solving a school bus scheduling problem with integer programming. European Journal of Operational Research.
Ibrahim, N., Adji, B., & Karim, M. (2013). Public Transport Passengers’ Perception and Demand Satisfaction: A Case Study at Petaling Jaya Municipal District, Malaysia. Proceedings of the Eastern Asia Society for Transportation Studies, 9(2006), 1–13.
Kelly, J. A., & Fu, M. (2014). Sustainable school commuting - understanding choices and identifying opportunities. A case study in Dublin, Ireland. Journal of Transport Geography, 34, 221–230. https://doi.org/10.1016/j.jtrangeo.2013.12.010
Kim, B., Kim, S., & Park, J. (2012). A school bus scheduling problem. European Journal of Operational Research, 218(2), 577–585. https://doi.org/10.1016/j.ejor.2011.11.035
Kinable, J., Spieksma, F., & Vanden, G. (2014). School bus routing: A column generation approach. INTERNATIONAL TRANSACTIONS IN OPERATIONAL RESEARCH, 453–478.
Nasrudin, N., & Nor, A. R. M. (2013). Travelling to School: Transportation Selection by Parents and Awareness towards Sustainable Transportation. Procedia Environmental Sciences, 17, 392–400. https://doi.org/10.1016/j.proenv.2013.02.052
Olivera, A. (2004). Heurísticas para Problemas de Ruteo de Vehículos. Montevideo: Universidad de la República.
Park, J., & Kim, B.-I. (2010). The school bus routing problem: A review. European Journal of Operatioanl Research, 311-319.
Rocha, L., González, E., & Orejuela, J. (2011). Una revisión al estado del arte del problema de ruteo de vehículos. Ingeniería, 16(2), 35-55.
Toth, P., & Vigo, D. (2002). The Vehicle Routing Problem. Computers and Operations Research, 235-245
Yigit, T., & Unsal, O. (2016). Using the ant colony algorithm for real-time automatic route of school buses. International Arab Journal of Information Technology, 13(5), 559–565. Retrieved from https://www.scopus.com/inward/record.uri?eid=2-s2.0-84990068901&partnerID=40&md5=e5a6235ef4076e0ce68f89d73045a011
1. Ingeniero Industrial, Universidad del Valle, Cali, Colombia, Facultad de ingenierías, Escuela de ingeniería daniel.escobar@correounivalle.edu.co
2. Ingeniero Industrial, Universidad del Valle, Cali, Colombia, Facultad de ingenierías, Escuela de ingeniería industrial. juan.gaviria@correounivalle.edu.co
3. Profesor Tiempo completo, Universidad del Valle, Cali, Colombia, Facultad de ingenierías, Escuela de ingeniería industrial. Master en Ingeniería industrial, Ingeniero industrial, universidad del Valle. juan.orejuela@correounivalle.edu.co