ISSN 0798 1015

Vol. 39 (Number 46) Year 2018. Page 35

Implementation of continuity in teaching stochastics to schoolchildren: from theory to practice (experience of the Russian school)

Implementación de la continuidad en la enseñanza estocástica a escolares: de la teoría a la práctica (experiencia de la escuela rusa)

Sergey Viktorovich SHCHERBATYKH 1; Anna Yurievna POLYAKOVA 2

Received: 15/06/2018 • Approved: 20/07/2018

Contents

1. Introduction

2. Methodology

3. Results

4. Conclusions

Acknowledgements

Bibliographic references

1. Introduction

Including the elements of statistics, combinatorics and probability theory in the existing school curricula is a highly important aspect of modernizing the content of mathematical education. This statement is due to the fact that the probabilistic and statistical knowledge plays a significant role in the general education of a modern person. The propaedeutic work with one of the content-methodological throughlines in primary school (the line of stochastics in the course of secondary school mathematics) should be replaced by a solid introduction of the elements of this discipline into the general course of mathematics. In this connection, in order to put the above into practice, it is necessary to carry out a continuous stochastic training not only in the study of mathematics in primary school, but also during the transition from primary to secondary school, that is, in the course of mathematics of the 5th year, and later throughout the entire academic program of secondary school. Thus, it becomes necessary to identify possible ways of implementing the continuous stochastic training of students.

Through modernizing the system of lessons in the mathematical cycle with the synchronized introduction of integrity, comprehensiveness and individualization in the educational process, as well as with maintaining continuous links in the study of mathematics, it has been proved that schoolchildren can continuously and systematically grasp the probabilistic-statistical part with a visible result.

1.1. Research background

A number of studies carried out by domestic and foreign methodologists are devoted to the development of theory and methods of teaching the elements of stochastics. For the most part, these studies focus on the possible methods of teaching statistics, combinatorics and the probability theory in secondary school. However, continuity of studying the stochastic part of the school course of mathematics in the transition from primary to secondary school and from secondary to higher one still remains poorly studied (Shcherbatykh and Polyakova, 2017).

In the process of study, a synthesis of theoretical and methodological framework was used, including:

1) the theoretical foundations for the general theory of learning, learning activity and the system-activity approach;

2) the concept of federal state educational standards and the theory of basic general education content;

3) the fundamentals of continuous education;

4) the fundamentals of continuity in mathematical education;

5) the fundamentals of continuity in education;

6) the fundamentals of continuity in teaching mathematics between primary and secondary, secondary and higher school.

Based on the theoretical and methodological foundations of the above authors, the authors propose the following ways of implementing continuity in teaching the elements of statistics, combinatorics and probability theory to schoolchildren - the introduction of comprehensiveness, integrity, continuity and individualization into the educational process in the lessons of mathematics. Each of these ways is described in detail.

1.2. Comprehensiveness of educational process in the study of stochastics

The comprehensiveness of educational process means uniting the pupils of primary, secondary and higher school by a common goal of gaining thorough knowledge of statistics, combinatorics and probability theory (Shcherbatykh and Polyakova, 2017).

The comprehensiveness of educational process presupposes that pupils should be responsible, attentive in studying this section of mathematics; they should strive to gain new theoretical knowledge, and to put it into practice later.

However, aspiration is not always helpful, since the problem of abilities often comes to the forefront, which is a broad theme for studying by psychologists both in Russia and abroad.

Currently, there are two approaches that consider the concept of “ability” completely differently.

In terms of the personality-activity-based approach, the correspondence between the person's neuropsychic features and the requirements of an activity is established. If the pupils' abilities do not meet the requirements for their mental and physical abilities needed for the process of complex and many-sided educational activities they are supposed to do, then the schoolchildren are not able to demonstrate a high level of performance.

A distinctive feature of the functional-genetic approach is the recognition of the fact that abilities are inherent and genetically conditioned.

Apart from considering the two approaches to the definition of abilities, the following types of abilities are also singled out: general abilities (which are sometimes called a person's general talent) and specific abilities (which are manifested in a specific activity).

The authors specify some parameters on the basis of which the presence of mathematical abilities can be revealed (mathematical abilities are a type of specific abilities) in schoolchildren during the study of stochastics:

1) formalizing the stochastic material, operating the formal structures of relations and links;

2) generalizing the stochastic material, singling out the primary and secondary elements;

3) operating the numbers and character symbols;

4) reducing the process of reasoning, the possibility of thinking in folded structures;

5) reversibility of the thinking process;

6) flexibility of thinking, ingenuity of thinking, freedom of thought;

7) stochastic memory;

8) analysis of a mathematical structure, rearrangement of its elements.

Based on the above parameters, mathematical abilities are organized in two main groups. The first group comprises the general characteristics of pupils' stochastic thinking or their mental activity in the stochastic field. The second one includes the parameters of mathematical abilities associated with the students' activities in the process of studying the stochastic material.

Thus, all schoolchildren (from the 1st to the 11th years of studies) can be united by the goal of gaining the knowledge of statistics, combinatorics and probability theory, but the result of mastering the knowledge is not always positive. Each pupil is different, and in this regard, those pupils whose abilities are at a zero level need a special approach.

1.3. Integrity of educational process in the study of stochastics

The concept of “holistic” is applied to many characteristics of pedagogical reality. In this regard, it is widely accepted to talk about holistic knowledge, the integrity of the content and the system of educational methods, and the holistic educational process (Serikov, 2012).

The integrity of the educational process in studying the elements of the probability-statistical part of the school course of mathematics in the conditions of continuity systematizes not only the activities of pupils and teachers in the lesson, but also the pupils' acquired knowledge and skills, scientific facts and other theoretical knowledge into a single whole (Shcherbatykh and Polyakova, 2017).

The authors believe that while pupils are learning the basics of statistics, combinatorics and probability theory, the regularities of a holistic educational process are as follows:

- its dependence (with setting goals and objectives as well as the development of content, methods and forms of teaching) on the ideology of the class and the pupils' needs;

- the dependence of the used methods, means and forms of instruction on the students' individual abilities and on the conditions in which the learning activity takes place;

- the interrelation between education and the development of a student's personality;

- the unity of upbringing and self-education, education and self-education;

- the development of the each student's personality in the activity;

- the interrelation between a class and an individual student in the educational process;

- the connection between the content, means, methods and forms of instruction.

1.4. Continuity of educational process in the study of stochastics

The continuity of educational process is inseparable from the integrity, its general philosophical meaning understands it as “the connection between different stages of development, the essence of which is the preservation of certain elements of the whole or its individual characteristics in the transition to a new state” (Nemov, 2003).

However, by succession, A.Kh. Shklyar means not only “a gradual transition from one level of education to another”, but also a successive change in the “level of requirements for the volume and depth of mastering knowledge and skills,” the organic “interconnection between content, the main methods and forms of the educational process at different levels of study as well as in different types of educational institutions” (Shklyar, 1995 ).

According to E.V. Smykalova, “The concept of continuity is applicable to objects that already have a definite structure, and only in this case it is possible to compare two possible states. Such comparison makes it possible to understand which elements and connections have changed, and which have passed into a new state successively” (Smykalova, 2004).

K.I. Neshkov connects the notion of continuity with repetition of the previously studied material: “... continuity requires ... repetition that ensures the continuous development of a system of concepts ... and as the topic develops, it must change accordingly, without being reduced to a mechanical repetition of the same exercises” (Neshkov, 1978).

V.M. Turkina (2003) outlined two aspects of continuity in education - procedural and informative. V.M. Turkina's point of view was also shared by I.O. Kovpak in her thesis (Kovpak, 2015) comparing the main content and requirements for the results of learning stochastic elements, as well as the level of mastering them according to the Federal State Educational Standards for primary (A sample educational program of educational institution Elementary School, 2013, Savinov, 2008) and general educational establishments (A sample program of educational institution, 2011, Approximate programs for subjects, 2010).

The viewpoint expressed by V.M. Turkina and I.O. Kovpak is shared by the authors and in this regard recommendations for implementing continuous teaching of stochastics in a secondary school are proposed.

For the transition of students from primary school to secondary school, and after - to the higher one, special training is required, which implies that a mathematics teacher must take care that the covered program fits the one that the pupils are supposed to cover in future. In addition, there should be no abrupt transitions in organizational forms, methods and content of teaching.

A teacher needs to be objective, strict and principled: liberalization in the assessment of students' knowledge or overrating is not allowed. The transfer of pupils to the next grade (especially from the fourth to the fifth grade) should be accompanied by the teacher's confidence in the pupils' knowledge in accordance with the current standard of education.

A teacher of mathematics should encourage the creation of conditions for psychological comfort, foster the development of students' mental activity when studying the elements of statistics, combinatorics and probability theory.

It is compulsory to take into account each child's age characteristics, schoolchildren's memory should not be overloaded, so the following tested didactic chain of a pupil's actions should be practiced in the lesson: “I saw — I heard — I did — I remembered — I understood!”

The lessons of stochastics should be accompanied by the development of schoolchildren's independence in taking the most optimal decision while choosing from all possible options. Along with this, the learners' ability to think critically should be formed.

Relying on the advanced, now very popular information and communication forms, methods and means of teaching it is necessary to maintain and develop students' interest in the probabilistic-statistical part of the school course of mathematics.

In order to improve the educational process, a teacher needs to analyze the results of their professional activity, assessing the successes and failures, and to subsequently develop a new educational plan.

The methods of teaching statistics, combinatorics and probability theory can be diverse. The authors propose a methodology with the active introduction of information and communication technologies in the lessons, which will allow students to develop a number of academic skills and qualities, the integration of which will determine the level to which the students' stochastic culture is formed.

1.5. Individualization of educational process in the study of stochastics

Teaching stochastics in school requires taking into account the students' individual characteristics (Polyakova, 2016). As V.A. Gusev (2003) noted, the system of such features (differences) forms the structure of schoolchildren's mental development. The level of acquiring knowledge, the level of mastering the generalized techniques and methods of operating knowledge and the level of aptitude for learning are indicated in the system of differences.

The dynamics of knowledge acquisition includes the following stages:

1) The assimilation of concepts is a process that has long been studied by psychologists who mark a purely individual movement in the mastery of concepts. The assimilation of the stochastic concepts has a very unusual character.

Thus, from the existing definitions of probability (statistical, classical, geometric, axiomatic), each schoolchild can choose for themselves the most understandable one for memorization and later master it. In rare cases, students comprehend the meaning of all these definitions.

2) Mastering the structure of mental operations, based on the methods of analysis and synthesis. According to N.A. Menchinskaya (1989), the degree of analysis and synthesis development is characterized by two criteria: the level of each operation performance with the help of differentiation, the transition from partial synthesis to the full one; the degree to which the levels of operations correspond to each other and their inseparable connection. Analysis and synthesis are the basic elements of generalization and abstraction, the drawbacks of which are based on the quality of performing more complex mental operations. However, when studying stochastics, schoolchildren's activity should combine not only analysis and synthesis, deduction and induction, specification and generalization, but also logic and intuition.

3) Mastering the interrelations between knowledge application and assimilation. In the process of mastering knowledge a student is required to apply the acquired knowledge in practice. However, the application of knowledge organized by the teacher does not often coincide with the student's independent use of this knowledge in different conditions. In this regard, the issue of applying knowledge while teaching stochastics increasingly depends on the schoolchildren's individual abilities.

4) The disclosure of interactions between theoretical and practical, abstract and concrete thinking. These interactions, significantly changing with age, should be known and taken into account in the process of teaching stochastics. P.P. Blonsky (1979) established the patterns according to which thinking can develop in two opposite directions: towards a more abstract one as well as towards a more concrete one. In this vein, as defined by S.V. Shcherbatykh (2011), stochastic thinking is formed as a result of teaching stochastics and allows to adequately perceive and analyze processes of a random nature, and is also able to develop both with regard to abstraction as well as concretization. Therefore, the formation of stochastic thinking is the main psychological innovation in the study of the stochastic line, which makes it possible to clearly position the developing character of teaching probability theory, mathematical statistics and combinatorics to schoolchildren.

5) Determination of goals for the effective formation of mental operations, the study of method formation process. Mastering a method requires not only the formation of an appropriate mental operation, but also the emergence of reasons and needs for using the operation as a method of work. In the future, the question of the reason for using the method turns into a deeper problem, which consists in the schoolchildren's need to carry out their educational activities. Such needs arise as a result of the long formation of mental activity methods in the process of learning stochastics.

Ultimately, individualization of the mastering knowledge process and some levels of applying this knowledge underlies the differentiation of levels in learning stochastics in school. Only when acquiring this quality can students understand the meaning of the studied stochastics material, feel their strength in its application in practice, form an interest in the subject, which will possibly underlie all their further activity.

The level of mastering the generalized techniques and methods of operating the knowledge of stochastics should be understood as a super task. If the stochastic knowledge itself is a well-studied object, then the activity in the field of stochastics and the techniques used in this activity have not been sufficiently studied. In accordance with the directions of the educational process within the stochastic framework, it is viable to create an exercise system that forms techniques for thinking activity (analysis and synthesis). This system of exercises can be used for different groups of students with different abilities and characteristics.

The level of aptitude for learning is a term widely used in psychological and pedagogical literature in the studies done by B.A. Ananiev (1977), G.A. Berulava (1990; 1993), S.F. Buykov, (1967), A.F. Govorkova (1962), L.G. Zhabitskaya (1972), S.F Zhuykov (1971); A.Ya. Ivanova (1976), Z.I. Kalmykova (1981; 1982), A.I. Kochetov (1996), N.A. Menchinskaya (1966; 1989) and others.

The scholars define the content of this concept from different perspectives. Thus, according to Z.I. Kalmykova (1981; 1982), aptitude for learning represents a system of a person's intellectual properties, characteristics of the mind, on which the productivity of educational activity depends. N.A. Menchinskaya speaks of the aptitude for learning as the ability to achieve a higher level of knowledge in a shorter period of time. From A.Ya. Ivanova's (1976) point of view, the aptitude for learning is a potential possibility of mastering new knowledge. S.F. Zhuykov (1971) characterizes this concept as a complex property, on which the success of learning depends.

Apart from this, the aptitude for learning can be general and specific (Menchinskaya, 1966; 1989), theoretical and practical (Kochetov, 1996). The theoretical aptitude for learning stochastics is related to the level to which stochastic thinking is developed and is determined by such indicators as the ability to find the logical connection between phenomena, the ability to see the differences between random opposite and similar phenomena, the ability to analyze, prove, refute or defend any point of view when solving stochastic tasks, the ability to see the main causes of what is happening during the experiments as well as the ability to self-analyze and self-evaluate the mental work. The practical aptitude for learning stochastics is connected with life experience and its comprehension with the help of stochastic knowledge obtained in school, revealing the laws of the environment, etc. It is here that there arise contradictions between knowledge and its application, theory and practice.

The aptitude for learning stochastics is indicated by five qualities: the depth of mind, the flexibility of mind, the stability of mind, the reflexivity of mind and the independence of mind.

The depth of mind is the generalization of mental activity in the field of stochastics, or the degree of significance of the signs and regularities that the schoolchild is able to identify in a phenomenon (experience, task). The formation of this indicator of learning capacity is associated with the formation of a student's thinking activity methods. The depth of mind is often referred to as its dynamism or mobility.

The flexibility of mind is the ability to creatively search for new solutions to non-standard problems of stochastics in the changing conditions of reality and the specifics of problems. It is indicated by approaching a task as a problem, viable variations of the methods of actions, the ease of restructuring knowledge or skills and their systems in accordance with the changed conditions as well as the ease of transition from one action to another.

The stability of mind is an internal plan of action, the ability to consciously retain in mind an indicated system of phenomenon and process features, without being distracted by any external phenomena.

Awareness or reflexivity of mind is the ability to realize not only the result, but also the course of solving a stochastic problem, to translate them into the language of words, to form an algorithm, typical methods and ways of solving tasks.

The independence of mind is an external, well-expressed feature of productive thinking. It manifests itself in an active search for new knowledge of probability theory, mathematical statistics and combinatorics, ways of solving tasks, in the particular ease with which schoolchildren perceive the teacher's help as well as in taking mistakes into account. The independence of mind takes place within all the qualities formulated above.

In the school, in order to improve the structure of the students' mental development in learning stochastics, the elements of combinatorics, statistics and probability theory must be firmly laid down, and it is at this time, “.... when the mind is mobile and the ideas communicated at this time become a working tool for life. To achieve this, instead of introducing a new subject at school, it is necessary to rationally distribute the necessary information within the existing subjects” (Gnedenko, 1982).

An important role in increasing the effectiveness of the educational and cognitive process in teaching stochastics is the identification of typological groups of students. A teacher simply needs to know the essential typological features inherent in a particular group of schoolchildren. However, the definition of such typological groups is not an easy task for solving which it is necessary to overcome some difficulties, among which are the following:

1) singling out the students' positive and negative characteristics, on which the whole educational process depends, can only be carried out by a narrow specialist in an integrated approach using specific diagnostics;

2) the difficulty of establishing links between the mechanisms of the educational process and the schoolchildren's individual characteristics;

3) specific methodological difficulties in the selection and differentiation of stochastics teaching content, in the development of methods for individualizing educational activities, in creating reasons for learning, etc.

In psychology, categories of people are distinguished according to the type of behavior (this is indicated by the corresponding type of personality) and by the type of personality. Students can be classified in the same way. Schoolchildren fall under two categories. Extroverts are active schoolchildren whose activities are directed outwards, towards others. Introverts are schoolchildren with such type of behavior, which directs their manifestations inwards, towards themselves. It has been established that extroverts are predominant in Russian schools, but nevertheless, it is very difficult to draw a distinction between them. According to the type of personality, students are divided into four categories: sanguine (active, strong and balanced), choleric (active, strong and unbalanced), phlegmatic (inactive, strong and balanced), melancholic (weak). Studies of such typification, conducted by a school psychologist, can be used by the teacher both in teaching and in educational work.

Moreover, the information on the above-mentioned categories of schoolchildren will not give the teacher an opportunity to judge the effectiveness of the educational process and guide it in the right direction. The effectiveness of teaching a subject (in this case - stochastics) is established after revealing the level of schoolchildren's aptitude for learning and their development.

Relying on the study done by E.A. Shumilin (1979), the authors single out three groups of schoolchildren formed in the process of learning stochastics.

In the first group, the schoolchildren's personality is characterized by the fact that they cannot be classified as intellectually passive people, although the academic progress of these students is very unstable. They lack a sense of purpose, perseverance, systematic actions and strong skills of independent work in the process of studying the stochastic material.

The schoolchildren belonging to the second group are efficient and purposeful. This category is the most trouble-free one, but satisfactory and good marks predominate for the subject.

The personality of schoolchildren in the third group is marked by the fact that they have a steady interest in stochastics combined with excellent academic performance.

The above-mentioned typological groups of schoolchildren are determined primarily on the basis of students' individual personal qualities, features and abilities to learn the stochastic material.

The theoretical information about the typological groups of students, as well as the system of their individual characteristics (differences), proposed by V.A. Gusev (2003), make it possible to argue that when covering stochastic material in the lessons of mathematics, it is necessary to use the pupils' individual learning tracks developed by the teacher in advance. The development of such tracks will require the teacher to skillfully vary the teaching material, correctly determine the learning objectives, and select the most effective methods and forms of teaching, which will be further used in the educational process (Polyakova and Shcherbatykh, 2017).

Individualization of teaching presupposes that the teacher should develop a system of tasks of different volume and levels of complexity, differentiate the material, and implement a certain system of measures for organizing the educational process in a particular learning group, whether it is strong or weak.

For schoolchildren, the individualization of learning provides an opportunity for their purposeful, creative development, the possibility of seeing the goal of their activity, the possibility of setting and performing the necessary tasks in the course of learning. An individualized approach helps to increase the students' activity, strengthens their motivation and fosters the formation of progressive analytical thinking.

One of the most important elements of the educational process individualization is the consideration of schoolchildren's psychological characteristics, and the goal of individualization is to keep each child's individuality and to subsequently develop it.

In the course of implementing the individualized approach, the following requirements should be taken into account by the teacher:

- the unity of the developed technology of schoolchildren's individual learning;

- the opportunity to independently choose the system of working with each group of students;

- the opportunity to analyze the dynamics of a student's transition from one learning group to another;

- the opportunity to demonstrate teamwork with different categories of schoolchildren.

The authors note that individualized learning can take place in two forms, one of which involves the pupils' active participation in determining their own learning track, and the other form is characterized by the absence of such participation.

It is known that the individualization of the second form of teaching was in demand in the Russian education system up to the 90s of the 20th century. At the moment, the practical application of the first form, with the active assistance of children, is of high priority.

Among the forms of teaching schoolchildren, it is possible to distinguish not only the two above mentioned but also the forms of information and communication technologies that recently emerged: virtual lectures, forum-consultations, chat-seminars, webinars and web-quests. These information and communication forms of teaching together with information and communication teaching methods (computer testing, questionnaires, crowdsourcing, algorithmization of problem solving) were earlier described by the authors (Polyakova and Shcherbatykh, 2014; 2015; 2016).

Testing the ways of implementing continuity proposed by the authors in the course of teaching the elements of stochastics was carried out in Efremov city, in a Municipal State-Owned Educational Institution “School No. 3”, one of the schools of the Tula region. The experiment was carried out among all pupils of the 5th grade.

To confirm the effectiveness of introducing the comprehensiveness, integrity and individualization in the process of teaching mathematics with maintaining continuity in the teaching of this discipline, cross-sectional testing was carried out, including four tasks which focused on:

1) the comparison of information presented in a linear chart and table;

2) drawing a linear graph based on a given table;

3) an intuitive idea of an experience, forecast or outcome;

4) classifying events intuitively according to their qualitative characteristics, initial forecasting.

For each problem, the reliability of the differences between the percentage of control and experimental samples in which the effect was observed was determined using Fisher's angular transformation.

In the course of the study, the correct solution of the task was considered to be “the presence of the effect”, and at least one mistake made by a pupil in the process of solving the task was regarded as “no effect”.

The authors formulated the main and alternative hypotheses that are true for all four tasks (tasks):

- (the main hypothesis): “The proportion of students who correctly solved task N in the experimental group is not higher than that of the control group”.

- (an alternative hypothesis): “The proportion of students who correctly solved problem N in the experimental group is higher than that in the control group."

According to Figure 4, it is clear that the empirical value of the criterion has fallen into the zone of significance, so an alternative hypothesis H1 should be adopted and the zero hypothesis H0 should be rejected.

Thus, of the four tasks, the authors agreed to adopt an alternative hypothesis at the 5% level of significance only in one task, and in the remaining three, the main hypothesis was rejected with considerable confidence. Therefore, accepting the alternative hypothesis that the proportion of schoolchildren who correctly solved the N problem in the experimental group is greater than that of the control group, the authors proved the effectiveness of introducing the comprehensiveness, integrity and individualization into the process of teaching mathematics with maintaining continuity in teaching stochastics.

The results of hypothesis statistical test by the Fisher angular transformation can be generalized in Tables 1 to 4 for each of the tasks.

Table 1
The results of statistical testing of the hypothesis by the Fisher criterion (Task 1)

Table 2
The results of the hypothesis statistical testing by the Fisher criterion (Task 2)

Table 3
The results of the hypothesis statistical testing by the Fisher criterion (Task 3)

Table 4
The results of the hypothesis statistical testing by the Fisher criterion (Task 4)

Based on the experimental data reflected in Tables 1-4, the authors have constructed a comparative diagram of the test results in the control and experimental groups for a better graphic representation of the experiment (Figure 5).

Figure 5
A comparative diagram of the test results in the control and experimental groups

3.1. Discussion

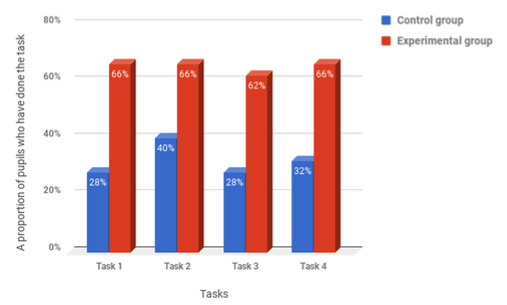
Thus, the comparative diagram of the obtained results showed that the problem of continuous stochastic preparation of students in a secondary school can be solved by implementing successive links in the study of a discipline, as well as the introduction of integrity, comprehensiveness and individualization in the learning process. The results that were obtained are significant, although they are not ideal. Further theoretical and methodological studies in the field of continuous teaching the probability-statistical elements to students will make it possible to carry out studies of a higher level in the future.

This study was devoted to the theoretical substantiation of possible ways of implementing the continuous teaching of stochastics to students and testing their effectiveness in practice.

The stated goals were achieved. The authors proposed a detailed description of each of the ways of implementing continuous stochastic preparation: comprehensiveness, integrity, continuity and individualization of the educational process.

The theoretical assumptions were tested by the authors in practice during the pedagogical experiment – the test one by the students of the 5th grade showed a visible result. The students of the experimental group coped with the tasks better than the schoolchildren of the control group.

Thus, implementation of the proposed ways of introducing continuity in the lessons of mathematics made learning the probability-statistical elements systematic, continuous and effective.

Acknowledgements

The study was carried out with the financial support from the Russian Foundation for Basic Research (Department of Humanities and Social Sciences), Project 17-36-01004 “Theoretical and methodological foundations for continuity and incessancy implementation in furtherance of the stochastic line in the school course in mathematics within the framework of system activity approach”.

Ananiev, B.G. (1977). Toward the problems of a modern human study. Moscow: Nauka.

Berulava, G.A. (1990). Psychodiagnostics of intellectual development of pupils. Novosibirsk: Novosibirsk State Pedagogical Institute Press.

Berulava, G.A. (1993). Diagnostics and development of teenagers' thinking. Biysk: Scientific Research Center of the Biysk State Pedagogical Institute

Blonsky, P. P. (1979). Chosen pedagogical and psychological compositions: In 2 vols. Vol. 1. Moscow: Pedagogika.

Buykov, S.D. (1967). Toward the problem of diagnostics of learning ability. Moscow: Prosveshcheniye

Gnedenko, B.V. (1982). The formation of the ideology of students in learning mathematics. Moscow: Prosveshchenie.

Govorkova, A.F. (1962). Experience of studying of some intellectual abilities. Issues of Psychology, 2, 83-91.

Gusev, V. A. (2003). Psychology and pedagogical bases of training in mathematics. Moscow: Verbum-M publishing house, Publishing Academy Center.

Ivanova, A. Ya. (1976) Learning ability as a principle of an intelligence quotient of children. Moscow: Moscow University Press.

Kalmykova, Z.I (1982). Toward the problem of diagnostics of intellectual development of school students. Issues of Psychology, 2, 74-79.

Kalmykova, Z.I. (1981). Productive thinking as learning ability basis. Moscow: Pedagogics.

Kochetov, A.I. (1996). Culture of a pedagogical research. Minsk: Adukatsiya i vykhavanne. ISBN: 985-6029-10-4.

Kovpak, I.O. (2015). The methodology of teaching stochastic elements in the course of mathematics for 5th-6th grades, implementing the requirements of the Federal State Educational Standards of the general secondary education. A candidate’s thesis. Moscow.

Menchinskaya, N.A. (1966). Training and intellectual development. Proceedings of the XVIII International Psychological Congress. Problems of Mental Development in Social Psychology, 3, 23–34. Moscow: Moscow University Press.

Menchinskaya, N.A. (1989). Problems of learning and intellectual development of the school student. Chosen psychological works. Moscow: Pedagogika. ISBN 5-7155-0198-9.

Nemov, R.S. (2003). Psychology: Dictionary-reference book: in 2 volumes. Vol. 1. Moscow: VLADOS-PRESS Publishing House.

Neshkov, K.I. (1978). Some issues of continuity when training in mathematics. In Continuity in training in mathematics. A grant for teachers. Originator A.M. Pyshkalo. Moscow: Prosveschenie.

Polyakova, A.Yu. (2016). Analysis of the mental development structure, the formation of typological groups and the determination of schoolchildren’s abilities to learn stochastics. Continuum: Mathematics. Computer Science. Education, 2. 87-92. Yelets: I.A. Bunin Yelets State University Press.

Sample programs for primary education: in 2 parts. (2008). Part 1. Moscow: Prosveshcheniye.

Savinov, E.S. (2012). A sample basic educational program for an educational institution. Primary school. 4th ed. Moscow: Prosveshcheniye. https://studfiles.net/preview/4540669/

Serikov, V.V. (2012). Subjective grounds for the integrity of the pedagogical process, News of the VSPU, 4 (68), 12 - 18.

Shcherbatykh, S.V. (2011). Methodological system of teaching stochastics in specialized classes of a secondary school. PhD Thesis in Education. Moscow.

Shcherbatykh, S.V., and Rogacheva (Polyakova) A.Yu. (2017). Continuity of the stochastic line of the school of mathematics: experience of the Russian education system. Revista ESPACIOS, 38(50) http://www.revistaespacios.com/a17v38n50/17385013.html.

Shcherbatykh, S.V., and Rogacheva (Polyakova), A. Yu. (2016). Model of the methodological system for learning stochastics to form the stochastic culture of pupils of the general education school with the means of new information and communication technologies. Proceedings of the International Scientific-Practical Conference: Developing the potential of information and communication technologies in the formation of a motivating educational environment. Varna, pp. 51-81.

Shcherbatykh, S.V., and Rogacheva (Polyakova), A.Yu. (2014). Application of “WEBQUEST” technology in teaching stochastics in the general education school. Proceedings of the International Scientific-Practical Conference: Information technologies in providing Federal State Educational Standards, 2, 196-198. Yelets: I.A. Bunin Yelets State University Press.

Shcherbatykh, S.V., and Rogacheva (Polyakova), A.Yu. (2015). A webinar as an essential component of distance learning (as exemplified by teaching elements of probability theory in a secondary school). Education, science and economics in schools and higher educational institutions. Proceedings of the International Scientific Conference: Integration into the international educational space. Armenia, Goris, Moscow, People’s Friendship University of Russia. Yerevan: Astghik Gratun, pp. 480-484.

Shcherbatykh, S.V., and Rogacheva (Polyakova), A.Yu. (2017). Realization of continuity in teaching the elements of stochastics to schoolchildren: Theoretical Aspects. European Journal of Social Sciences, 7, 371-373.

Shklyar, A.H. (1995). Continuous professional education in integrative structures of vocational school (the theory and practice). Minsk: MGVRK.

Shumilin, E. A. (1979). Psychological features of the identity of the senior. Moscow: Prosveshchenie.

Smykalova, E.V. (2004). Tasks with developing functions as a means of ensuring continuity in teaching mathematics between primary and secondary school. A candidate’s thesis. St. Petersburg.

Turkina, V.M. (2003). The introduction of continuity in the teaching of mathematics in the conditions of developmental learning. PhD thesis. St. Petersburg.

Zhabitskaya L.G. (1972). Psychological research of criteria of literary development. Issues of Psychology, 5, 89–100.

Zhuykov, S. F. (1971). Toward the problem of diagnostics of learning ability of school students. Issues of Psychology, 5, 85 – 99.

1. Doctor of Sciences (Education); Bunin Yelets State University, Yelets, Russian Federation. Contact e-mail: Scherbatych2017@yandex.ru

2. Bunin Yelets State University, Yelets, Russian Federation