ISSN 0798 1015

Vol. 39 (Nº 43) Ano 2018. Pág. 6

A educação do campo e as unidades de medidas agrárias

The field education and units of agrarian measures

Alcides José TRZASKACZ 1; Silton Jose DZIADZIO 2; Joyce Jaquelinne CAETANO 3

Recebido: 22/04/2018 • Aprovado: 07/06/2018

Conteúdo

1. Introdução

2. Metodologia

3. Desenvolvimento das atividades

4. Conclusões

Referências bibliográficas

1. Introdução

O homem desde as primeiras civilizações sentiu a necessidade de medir. No cotidiano os agricultores utilizam-se de artifícios próprios que lhes permitem interpretar números atribuídos a forma de medir. “A ação de medir é uma faculdade inerente ao homem, faz parte de seus atributos de inteligência” (SILVA, 2004, p.35).

Os artifícios são desenvolvidos pelo homem do campo de maneira a facilitar as operações matemáticas envolvidas nos cálculos de medidas de áreas de terra. Para Machado (2000, p.08) “a necessidade de medir é quase tão antiga quanto à necessidade de contar”. A matemática utilizada pelos agricultores passa de geração em geração e varia com a história de cada cultura, possibilitando a aplicação diária da matemática nos seus afazeres.

Nesse sentido, D’ Ambrósio (1996, p. 99) define Educação como sendo as estratégias criadas pela sociedade para facilitar a vivência comum e preparar para as atividades da vida cotidiana.

Partindo desse contexto, manifestou-se a curiosidade de conhecer a forma que os agricultores utilizam para medir e calcular áreas de terrenos usados para desenvolvimento da agricultura básica e relacionar esse conhecimento com a matemática escolar.

De acordo com as Diretrizes Curriculares Estaduais do Paraná (DCEs), que norteiam o processo de ensino da Educação Básica do referido estado, o conteúdo medidas de áreas deve ser abordado de forma significativa, sendo este, conteúdo fundamental para a formação do educando.

Dessa forma, no Ensino Fundamental, os educandos estudam Grandezas e Unidades de Medidas, calculando a área de figuras planas utilizando as unidades de medidas padrão, como o metro e o metro quadrado. Diante disso, as unidades de medidas como a braça, o litro, o hectare e o alqueire são desconsideradas, mesmo sendo medidas comuns aos agricultores. Sabemos que as unidades de medidas acima mencionadas fazem parte do cotidiano dos estudantes do campo, no entanto, não estão sendo associadas à matemática escolar.

Calcular a área de terrenos e trabalhar com unidades de medidas como a braça, litro, hectare e alqueire é primordial para quem habita no campo, pois aproxima o conteúdo escolar da realidade dos alunos facilitando assim o processo de ensino e aprendizagem. Dessa forma, a pesquisa buscou colaborar para a aprendizagem fundamentada na vivência dos educandos.

Para tanto, o objetivo do trabalho é estudar as Unidades de Medidas Agrárias e desenvolver cálculos que a relacionem com as Unidades de Medidas padronizadas, procurando dinamizar os conteúdos e tornar o ensino mais interessante e contextualizado.

1.1. Da Matemática Escolar

A Matemática desenvolveu-se em tempo e lugares diferentes, a partir de enigmas que afetavam povos antigos. Conceitos matemáticos foram criados para auxiliar na explicação, convivência e desenvolvimento do meio habitado pelo homem.

A matemática foi uma estratégia desenvolvida pela espécie humana ao longo de sua história para explicar, para entender, para manejar e conviver com a realidade sensível, perceptível, e com o seu imaginário, naturalmente dentro de um contexto natural e cultural (D’ AMBRÓSIO, 1996, p. 07).

Atualmente, a Matemática continua incluída na vivência das pessoas, desde simples tarefas rotineiras feitas por pessoas comuns até a realização de atividades complexas desenvolvidas por cientistas, estão sobrecarregadas de conceitos matemáticos.

Sendo a Matemática tão atuante na vida das pessoas, seu estudo na escola deveria ser interessante e de fácil compreensão. No entanto, “O ensino da Matemática está passando por uma situação de grande desconforto para quem aprende, para quem ensina, sendo também alvo de críticas da opinião pública” (VASCONCELOS, 2009, p.30). Os educandos se aborrecem ao estudar esta disciplina, apresentam dificuldades para compreender os conteúdos e a Matemática fica caracterizada como uma disciplina apavorante.

De acordo com Sadovsky (2007, p. 15), a dificuldade de aprendizagem e o baixo desempenho dos educandos em matemática não ocorrem só no Brasil, é uma realidade em muitos países. Alguns relatos demonstram os conteúdos matemáticos como estranhos, sem sentido, configurando a disciplina como um “monstro” para os alunos.

Se a matemática ensinada acarreta dificuldade de aprendizagem é necessário buscar novos métodos de ensino. Nessa perspectiva, surge na segunda metade do século XX a Educação Matemática, cujo objetivo é orientar o ensino e a aprendizagem dessa disciplina de forma significativa, crítica e interdisciplinar, fugindo da educação tradicional e tecnicista.

Nesse contexto, a matemática e a Educação Matemática (EM) passaram a ser vistas como práticas socioculturais que atendem a determinados interesses sociais e políticos. São inúmeras as pesquisas que procuram investigar a relação entre a cultura da matemática escolar, a cultura matemática que o aluno traz para a escola e a cultura matemática produzida pelos trabalhadores (adultos e algumas crianças trabalhadoras) ao realizar suas atividades profissionais (Fiorentini &Lorenzato, 2007, p. 51).

Assim, estudar matemática não se resume em aplicar fórmulas, repetir conceitos prontos, mas se envolver em atividades dinâmicas que dão sentido aos conteúdos. Mais importante que encontrar a resposta correta de um exercício é compreender os mecanismos envolvidos que levaram a resposta.

Pozo (2002) diz que “[...] na aprendizagem é preciso procurar sempre um motivo”, ou seja, é necessário que os conteúdos matemáticos sejam interligados com questões cotidianas, exercícios mecânicos e repetitivos cederem espaço a atividades que envolvam matemática e preparem para o convívio em sociedade.

No que se refere à atuação do professor na Educação Matemática, temos um profissional cuja função é promover o diálogo, a construção de conceitos, atuando como um mediador do conhecimento, e não como o dono do saber como na Educação tradicional. Para Scandiuzzi (2005, p. 190)

O professor não é mais aquele que detém o saber, o poder, o conhecimento. Ele é uma pessoa que interage com um grupo que detém um saber diferenciado do dele e, através do diálogo, o conhecimento é produzido nas duas direções – professor/aluno e aluno/professor [...].

Se conteúdos são relacionados com questões sociais, econômicas, políticas e ambientais, então, a escola não ensina só Matemática, mas educa por meio da Matemática. Esse “educar”, entre outros aspectos, pressupõe a construção e o desenvolvimento de uma atitude democrática por parte dos educandos.

Na Educação Matemática o desenvolvimento de uma atitude democrática é fundamental, almejando a

[...] formação matemática dos alunos não apenas para instrumentalizá-los matematicamente, mas também para fazê-los refletir sobre a presença da matemática na sociedade, seja em benfeitorias ou em problemas sociais, e reagir contra as situações que a matemática também ajudou a construir (ARAÚJO, 2007, p. 34).

Essa nova proposta que surge, prevê a mudança de um ensino de Matemática para uma Educação Matemática. Abstrações, decorebas de regras e resoluções de exercícios sem aplicação dão lugar a atividades dinâmicas, a resoluções de problemas que fazem dos conteúdos matemáticos um suporte na preparação para o futuro.

1.2. Da Educação do Campo

No século XIX e início do século XX, as políticas públicas mostravam pouco interesse em relação à educação rural. Conforme afirma Ferrari citado por Silva (2005, p. 01), havia um elevado nível de analfabetismo das populações rurais, se comparado com a área urbana. A educação nas escolas rurais também era vista como atrasada e de baixa qualidade, muitas vezes escapando da vivência dos educandos.

Para compensar tal realidade surgiu a Educação do Campo, com o objetivo de promover o desenvolvimento cultural, social e econômico de pessoas que sobrevivem no meio rural. Conforme destaca Ferreira e Batista (2006, p. 02) sua tarefa é o desenvolvimento daqueles que vivem e constroem sua história no campo.

A concepção de Educação do Campo está voltada para o trabalhador do campo dando-lhe a oportunidade de acesso a uma educação de qualidade, que prevê o desenvolvimento sustentável nas unidades de produção familiar. Segundo Souza (2008, p. 1090)

[...] a educação do campo expressa uma nova concepção quanto ao campo, o camponês ou trabalhador rural, fortalecendo o caráter de classe nas lutas em torno da educação. Em contrapondo à visão de camponês e de rural como sinônimo de arcaico e atrasado, a concepção de educação do campo valoriza os conhecimentos da prática social dos camponeses e enfatiza o campo como lugar de trabalho, moradia, lazer, sociabilidade, identidade, enfim, como lugar da construção de novas possibilidades de reprodução social e de desenvolvimento sustentável.

Desse modo, o modelo de Educação do Campo garante um ensino compromissado com o desenvolvimento da extensão rural, caracterizando-se como um espaço de compensar as precariedades do antigo ensino rural, marcado pelo analfabetismo e baixa qualidade de ensino.

Caldart (2004) expressa que o grande desafio da Educação do Campo é propor experiências e debater ideias que possam nortear o projeto e práticas da política educacional do campo. De acordo com a autora, se faz fundamental rever as práticas de sala de aula em escolas do campo, visando aproximar os conteúdos às especificidades dos estudantes que a frequentam.

Em relação ao ensino de matemática para a Educação do Campo, D’Ambrósio (1998, p. 17), afirma que:

Cada grupo cultural tem suas formas de matematizar. Não há como ignorar isso e não respeitar essas particularidades [...] todo o passado cultural da criança deve ser respeitado. Isso não só lhe dará confiança em seu próprio conhecimento, como também lhe dará certa dignidade cultural ao ver suas origens culturais sendo aceitas por seu mestre e desse modo saber que esse respeito se estende também a sua família e a sua cultura.

No entanto, observamos que poucos são os relatos de atividades diferenciadas em matemática que contemplam a realidade e o conhecimento dos estudantes, conforme pressupõe a Educação do Campo. Nessa perspectiva, com esse trabalho visamos propor e discutir uma abordagem para o tema de unidades de medidas, contemplando os saberes e a vivência dos camponeses, em consonância com a proposta de Educação do Campo.

Esse trabalho consiste em uma pesquisa de cunho qualitativo, onde foi entrevistado um agricultor de uma comunidade agrícola da região de Irati-PR, com o objetivo de conhecer as unidades de medidas agrárias regionais e as diferentes formas de calcular e medir áreas de terrenos agrícolas.

Partindo das unidades de medidas relatadas pelo agricultor e de posse de alguns instrumentos de medir utilizados no cotidiano da atividade agrícola, estas foram apresentadas aos educandos do Ensino Fundamental de uma escola do campo, visto que, os conteúdos Unidades de Medidas e Cálculo de Área fazem parte do programa de ensino proposto pelas Diretrizes Curriculares do Estado do Paraná.

Nas aulas, foram abordadas as unidades de medidas como a braça, o litro, o hectare, o alqueire e o cálculo de área de terrenos envolvendo os métodos utilizados pelos agricultores da região. A partir disso, buscamos trabalhar os conteúdos de forma contextualizada e promover uma discussão apropriada acerca da relação entre as medidas padronizadas e as unidades de medidas utilizadas no cotidiano do homem do campo.

As atividades foram desenvolvidas em uma turma do 9o do Ensino Fundamental contendo 18 estudantes, e foram organizadas de modo que os educandos visualizassem na prática as unidades de medidas citadas.

Como técnica de coleta de dados, durante a realização das atividades optou-se por observações e relatos dos educandos, pois de acordo com Marconi e Lakatos (2007), essa técnica de pesquisa utiliza os sentidos e se torna apropriada, quando objetivamos obter aspectos de uma realidade em estudo, “Não consiste apenas em ver e ouvir, mas também em examinar os fatos ou fenômenos que se deseja estudar” (p.88).

Inicialmente os educandos foram instruídos a perguntar aos pais, parentes ou vizinhos, como eles fazem para medir os terrenos de suas plantações. Como resultado percebeu-se que a maioria dos agricultores conhecem as Unidades de Medidas Agrárias e utilizam nas atividades do campo. Na Figura1, mostramos a pesquisa desenvolvida por um estudante.

Tendo feito um apanhado geral sobre as atividades a serem desenvolvidas, apresentaram-se as Unidades de Medidas Agrárias e suas relações com as Unidades de Medidas padronizadas.

São inúmeras as unidades de medidas de superfície ao longo da história dos povos. No Brasil, há unidades agrárias que ainda são utilizadas, quase todas derivam da medida “braça”, que equivale 2,2 metros.

Figura 1
Resultado da pesquisa de educando

Fonte: Os autores.

São inúmeras as unidades de medidas de superfície ao longo da história dos povos. No Brasil, há unidades agrárias que ainda são utilizadas, quase todas derivam da medida “braça”, que equivale 2,2 metros.

O “alqueire” é uma das principais unidades de medidas agrárias, sendo variável de acordo com o número de litros de plantio de milho que comporta, segundo costumes locais, a semeadura de um litro (capacidade) de sementes debulhadas, num compasso de um metro quadrado ( ), para cinco ou seis grãos, cobrindo uma área de 605 . Um alqueire corresponde a 40 litros, logo, um alqueire tem 24.200m2.

O “hectare” é a unidade de medida que corresponde 10.000 m2, tendo aproximadamente 16,53 litros, sendo que, uma região retangular medindo 25x5 braças corresponde a 125 braças quadradas (uma braça quadrada 4,84m2), e, 125 braças quadradas correspondem a 1 litro (605m2).

Para trabalhar as unidades de medidas acima citadas, foram divididos os educandos em dois grupos, sendo eles nominados como: “Quarteto Fantástico” e “Nas Braças da Matemática”. Em seguida, os educandos foram instruídos a medir a um terreno irregular localizado nos fundos da escola e também a quadra de esportes. Para isso, utilizaram uma fita métrica e uma corda com 11 metros de comprimento, equivalente a cinco braças (Figura 2). A corda com este comprimento é utilizada pelos agricultores da região para calcular a área de pequenos terrenos, tanto em braças como em metros quadrados.

Figura 2
Instrumento para realização de medidas

Fonte: Os autores

Ambos os grupos realizaram as medidas dos terrenos sugeridos utilizando as duas formas de medir: metro quadrado, aprendido na sala de aula e, a braça quadrada, forma que os agricultores da região utilizam para medir.

A figura abaixo (Figura 3) representa as medidas do terreno nos fundos da escola, efetuadas pelo grupo “Quarteto Fantástico” utilizando uma corda, tendo como unidade de medida ‘braça’.

Figura 3
Medida do terreno utilizando a “braça”

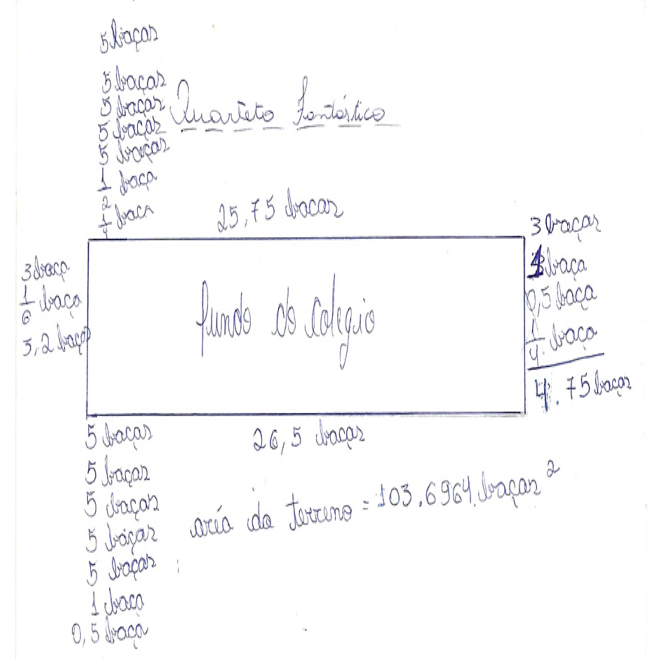
Fonte: Os Autores.

Após a coleta das medidas os grupos foram orientados a calcular a área, encontrando a média das medidas laterais opostas, e calculando o produto entre elas (Figura 4), conforme segue abaixo:

Figura 4
Cálculos da área do terreno.

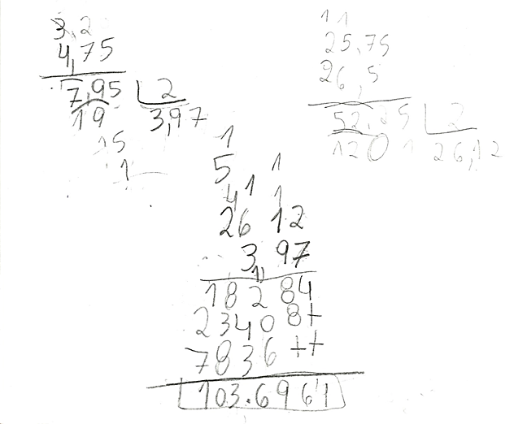
Fonte: Os Autores.

Passando para um modelo matemático, juntamente com os estudantes encontrou-se a seguinte fórmula para o cálculo da área:

A figura a seguir, representa o mesmo terreno, agora medido pelo grupo “Nas Braças da Matemática” utilizando a trena e tendo como unidade de medidas o ‘metro’.

Figura 5
Medida do terreno utilizando o “metro”

Fonte: Os Autores

Da mesma forma que anteriormente, para calcular a área (Figura 6), o grupo encontrou a média das medidas laterais opostas e calculou o produto entre elas:

Figura 6
Cálculo de área utilizando o metro

Fonte: Os Autores

Transformando o calculo em um modelo matemático, encontramos a seguinte fórmula para o cálculo da área:

Ao encerrar as atividades, pode-se afirmar que o trabalho serviu como uma importante mediação pedagógica.

O fato dos educandos realizarem a medida do terreno, calcularem a área e construírem um modelo matemático para o cálculo da área de terrenos irregulares, possibilitou que os conteúdos fossem abordados de modo mais dinâmico, atrativo e contextualizados.

Para obter as impressões dos educandos acerca das atividades realizadas, aplicou-se um questionário, buscando identificar se essa abordagem foi ou não importante e instigante para eles. Com as respostas, observamos que 100% dos estudantes revelaram ser mais interessante estudar Matemática desenvolvendo atividade práticas e 90% afirmaram ter mais atração e interesse pelos estudos quando essas contemplam sua realidade. Interesse, desafio e atração são fatores intercessores para a aprendizagem. De acordo com Moran (2000, p. 24) “Aprendemos mais, quando conseguimos juntar todos os fatores: temos interesse, motivação clara; desenvolvemos hábitos que facilitam o processo de aprendizagem; e sentimos prazer no que estudamos e na forma de fazê-lo”.

Ao desenvolver atividades complementares averiguou-se boa compreensão sobre os conteúdos. Com as respostas, pode-se afirmar que, para 90% dos educandos, as atividades mostraram a importância da Matemática no desenvolvimento de atividades rotineiras do dia-a-dia.

Ainda, no que diz respeito à motivação e interesse pelos estudos, compreensão e aplicação dos conteúdos, destacamos a seguir algumas palavras dos estudantes, captadas nas observações durante a realização das atividades:

A maneira como estamos medindo é a mesma que meu pai usa para medir área de plantios, inclusive com corda.

Que legal, agora sei calcular a área de terrenos.

Calculamos a área de duas maneiras diferentes e chegamos ao mesmo resultado em litros, deu para entender a relação entre braça e metro quadrado.

Encontramos a área do terreno e criamos uma fórmula que é possível calcular a área de outros terrenos.

Analisando os dados do questionário e depoimentos de alunos, foi possível constatar que o desenvolvimento das atividades garantiu um processo de ensino e aprendizagem de Matemática mais eficiente, preparando os educandos do campo para tarefas desenvolvidas no meio rural.

Ao finalizar este trabalho é importante lembrar o que se propôs no início da pesquisa: desenvolver atividades com Unidades de Medidas Agrárias, baseando em situações vivenciadas pelos alunos que habitam no campo.

Vale destacar também o que ressaltamos no referencial teórico: a importância de uma Educação Matemática, com atividades, mais próximas da realidade dos educandos e que a Educação do Campo é um sistema de ensino que busca valorizar os conhecimentos da prática social dos camponeses.

Diante disso, no desenvolvimento do trabalho ficou evidente que atividades envolvendo Unidades de Medidas Agrárias, trabalhando o conteúdo de modo prático e contextualizado, proporcionou maior interação dos educandos, com as variáveis em estudo, construindo e assimilando conceitos do cálculo de área.

Desse modo, não há como negar, que as atividades contribuíram para modificar as práticas de ensino que vigoram, considerando os dados coletados e observações, que revelaram que os educandos tiveram interação, interesse e motivação em realizar as atividades.

Com base neste trabalho, conclui-se que o profissional da Educação do Campo deve buscar a renovação do ambiente escolar, modificando metodologias tradicionais de ensino, principalmente no que se refere ao ensino de Matemática para o campo, que é uma ferramenta importante para o desenvolvimento de atividades agrícolas.

ARAÚJO, J. L. Educação Matemática Crítica na Formação de Pós-Graduandos em Educação Matemática. In: ARAÚJO, J. L. (org) Educação Matemática Crítica: reflexões e diálogos, Belo Horizonte: Argumentum, 2007. p. 25-38.

CALDART, R. S. A escola do campo em movimento. In.: ARROYO, Miguel Gonzáles; CALDART, R. S.; MOLINA, M. C.. (Orgs.). Por uma educação do campo. Petrópolis-RJ: Vozes, 2004.

D’ AMBROSIO, Ubiratan. Educação Matemática: Da Teoria a Pratica. Campinas: Papirus, 1996.

D’ AMBRÓSIO, Ubiratan. Etnomatemática – Arte ou Técnica de Explicar e Conhecer. São Paulo: Ática, 1998.

FERREIRA, J. A. S.; BATISTA, M. S. X. Fundamentos Sociológicos da Educação do Campo e a Formação Docente. In: X ENCONTRO DE INICIAÇÃO Á DOCÊNCIA.10., 2006, Recife. Anais... Recife, 2006.

FIORENTINI, D.; LORENZATO, S.. Investigação em Educação Matemática: percursos teóricos e metodológicos. 1ª Ed. Campinas: Autores Associados, 2007.

MACHADO, N. J. Medindo Comprimentos. São Paulo: Scipione, 2000.

MARCONI, M. A.; LAKATOS, E. M.. Técnicas de pesquisas: planejamento e execução de pesquisas, amostragens e técnicas de pesquisas, elaboração, análise e interpretação de dados. São Paulo: Atlas, 2007.

MORAN, J. M.. Ensino e Aprendizagem Inovadores com Tecnologias Audiovisuais e Telemáticas. In: MORAN, J. M.; MASSETO, M. T.; e BEHRENS, M. A.. Novas tecnologias e mediação pedagógica. Campinas: Papirus, 2000. p. 11 – 65.

POZO, J. I, Aprendizes e mestres: a nova cultura da aprendizagem. Porto Alegre: Artmed, 2002.

SADOVSKY, P. Falta Fundamentação Didática no Ensino da Matemática. Nova Escola, São Paulo, Ed. Abril, Jan./Fev. 2007.

SCANDIUZZI, P. P. Educação Matemática Indígena: a Constituição do Ser entre os Saberes e Fazeres. In: BICUDO, M. A. V.; BORBA, M. (Orgs.), Educação Matemática: pesquisa em movimento, 2 ed. São Paulo: Editora Cortez, 2005.

SILVA, I. História dos pesos e medidas. São Carlos: Edufscar, 2004.

SILVA, M. S. Educação de Campo e Desenvolvimento: uma relação construída ao longo da história. Recife, 2005. Disponível em:<http://www.contag.org.br/imagens/f299Educacao_do_Campo_e_Desenvolvimento_Sustentavel.pdf>. Acesso em: 26 de março de 2018.

SOUZA, M. A. Educação do Campo: Políticas, Práticas Pedagógicas e Produção Científica. Educ. Soc., Campinas, vol. 29, n. 105, p. 1089-1111, set./dez. 2008. Disponível em <http://www.cedes.unicamp.br. Acesso em: 26 de março de 2018.

VASCONCELOS, C. C. Ensino aprendizagem da matemática: velhos problemas, novos desafios. Revista Millenium n° 20, São Paulo, 2009.

1. Graduando do 4° ano do curso de Licenciatura em Matemática da Universidade Estadual do Centro-Oeste (Unicentro), campus de Irati. alcidestkz@gmail.com

2. Professor Colaborador. Departamento de Matemática. Universidade Estadual do Centro-Oeste (Unicentro), Campus Irati. silton.dziadzio@yahoo.com.br

3. Professora do Departamento de Matemática. Universidade Estadual do Centro-Oeste (Unicentro), campus de Irati. joyce.tardo@yahoo.com.br