ISSN 0798 1015

Vol. 39 (Nº 41) Año 2018 • Pág. 1

Caso de estudio para un proyecto de inversión minera, aplicando opción real de abandono mediante árboles binomiales y modelos de volatilidad condicional

Case study for a mining investment project, applying real option of abandonment using binomial trees and conditional volatility model

ARANGO, Mónica A. 1; MONTES, Luis F. 2; ARBOLEDA, Diana C. 3

Recibido: 24/03/2018 • Aprobado: 01/05/2018

Contenido

1. Introducción

2. Contribuciones en la valoración de proyectos en el sector minero

3. Metodología

4. Resultados

5. Conclusiones

Referencias bibliográficas

1. Introducción

El Precio del oro es el factor de mayor relevancia para las empresas del sector minero, sus particularidades en cuanto a distribución geográfica a nivel mundial y su característica de metal precioso lo convierten en un activo fácil de transar en los mercados internacionales. Su característica de agotabilidad y su escasez implican una elevada volatilidad del precio, afectando las expectativas de rentabilidad de los inversionistas (Arango & Botero, 2017).

 De lo anterior, el precio de este commodity es un parámetro clave para la evaluación de proyectos en el sector minero y la toma de decisiones de inversión. Los métodos convencionales de flujo de caja descontado (FCD) se utilizan ampliamente para la valoración de este tipo de proyectos. Sin embargo, entre más profundo se encuentre el oro dentro de la mina, mayores serán los costos de extracción, por ende, se llegará a un punto donde los tomadores de decisiones suspendan la explotación del mineral, evitando la exposición al riesgo de no obtener los flujos de caja necesarios para cubrir los egresos.

En el campo de Finanzas Corporativas las teorías han avanzado considerando las flexibilidades en este tipo de tomas de decisiones. Así, Myers (1977) (Trigeorgis & Tsekrekos, 2018) expresan que el valor de una compañía no depende únicamente del valor presente de las expectativas futuras de flujo de caja, sino también del valor presente de las opciones reales futuras que puedan contemplarse, entre las cuales se encuentran las opciones de crecimiento o contracción, de abandono o aplazar, entre otras. Para ello, el autor se basa en los fundamentos de la valoración de opciones financieras.

En consecuencia, la aplicación de opciones reales es complemento de la valoración por métodos tradicionales. La combinación de esta herramienta con los FCD brinda una mayor precisión para estimar la viabilidad económica de un proyecto, en especial en el caso del sector minero, donde la incertidumbre y el agotamiento del recurso es evidente.

Este artículo se divide en cuatro secciones. En la primera se presentan aportes de la literatura internacional sobre la valoración de proyectos de inversión en el sector minero. En la segunda sección, se aborda la metodología de valoración tradicional por FCD y árboles binomiales. Así mismo, se presenta de manera introductoria los modelos de volatilidad empleado en la estimación. La tercera sección presenta los resultados de la valoración con opciones reales a través de árboles binomiales. La última sección presenta las conclusiones del caso de estudio.

La aplicación de Opciones Reales a empresas mineras fue iniciada por Brennan Schwartz (1985)  (Tanaka, Marilia, & Montero, 2016), que desarrolló un modelo de tiempo continuo de una Mina que puede cambiar entre dos estados de funcionamiento: Desde un estado inactivo a un estado activo, mediante el pago de un coste de activación hundido; y viceversa, de un estado activo a un estado inactivo, mediante el pago de una inactivación hundida costo. Los autores muestran que dicha mina está sujeta a histéresis, es decir, hay un intervalo en el precio de la materia prima extraída que hace que el estado operativo actual de la mina dependa de la historia pasada de los precios.

Siguiendo este estudio, Dixit (1989) (Guedes, 2017) adapta el modelo para estudiar las entradas y salidas decisiones de las empresas, encontrando un patrón similar de histéresis. Mason, 2001 Extiende el modelo para investigar una mina con reservas finitas, concluyendo que el grado de histéresis está relacionado negativamente con el tamaño restante de las reservas. Otros autores han probado empíricamente el ROA para la valoración de la mina Y gestión. Slade (2001) (Guedes, 2017) mide el valor de la flexibilidad gerencial utilizando un panel de 21 minas de cobre canadienses entre 1980 y 1993.  En contraste, Moel y Tufano (2002) (Guedes, 2017) analizan  el cierre de la mina y las decisiones de apertura utilizando una muestra de 285 Minas de oro durante el período 1988-1997, documentando pruebas histéresis, encontrando que es más probable que una mina permanezca abierta si se ha explotado durante un intervalo de tiempo continuo, a que sea puesta en servicio si se ha interrumpido su explotación.  

Otro capítulo de la literatura empírica sobre empresas de minería de oro examina las propiedades de la elasticidad del precio de las acciones de dichas firmas con respecto al precio del oro, designado comúnmente como betas del oro. Tufano (1998) (Guedes, 2017) sostiene que una mina de oro que está restringida a operar permanentemente hasta que sus reservas estén completamente agotadas Beta mayor que uno, debido a un efecto de apalancamiento operativo. Además, argumenta que la disponibilidad de opciones reales para tal mina, como la opción de cierre temporal, debe reducir la beta del oro. Usando una muestra de 48 empresas norteamericanas de minería aurífera entre 1990 y 1990, estima una beta promedio de oro superior a uno, un hallazgo que sugiere que los efectos de amplificación del apalancamiento operativo y financiero sobre las ganancias de oro superan el efecto de mitigación resultante de la disponibilidad de opciones reales. Este resultado corrobora a Blose y Shieh (1995) (Reboredo & Ugolini, 2017) que, a partir de una muestra de 23 empresas de minería de oro seleccionadas CRISP entre 1981 y 1990, estimar una beta media de oro por encima de uno.

La literatura recomienda el uso de las Opciones Reales OR como complemento a la valoración tradicional.  Ya que, permite la inclusión de la flexibilidad en la toma de decisiones gerenciales, ampliando el intervalo de posibles resultados futuros. En este contexto, el valor presente neto ajustado se estima como se indica en la siguiente expresión:

VPNA=VPN+OR

Dónde:

VPNA= Valor presente neto ajustado; VPN= Valor presente del Flujo de caja del proyecto descontado; OR= Valor de la opción real. En la tabla 1.  se presentan diferentes tipos de opciones y su descripción.  La selección del tipo de opción se define como uno de los aspectos de mayor dificultad al momento de realizar la valoración con esta metodología, por ello en la misma tabla mostramos el tipo de opción y la forma para estimar su valor.

Tabla 1
Tipos de opciones

Fuente: Elaboración propia

3.1. Arboles Binomiales

El modelo de valoración binomial más utilizado corresponde a la propuesta desarrollada por Cox, Ross y Rubinstein (1979) (Cox, Ross, & Rubinstein, 1979), del cual se derivan modelos como el de Boyle (1988) (Cuervo, Felipe,. Botero, 2014)  para valorar opciones con subyacentes en dos estados, conocido como Simulación Montecarlo. Así mismo, la literatura sobre el tema desarrolla estimaciones empíricas con modelos de valoración de opciones que combinan árboles binomiales con teoría de decisiones (Brandao, Dyer y Hahn, 2005; Rendleman y Bartter, 1979; Smith y Nau, 1995) (G. S. Milanesi, 2016).

Esta metodología por su versatilidad se adapta a distintas modalidades y adecuaciones según se trabaje modelando el proceso estocástico con rejillas recombinantes de nodos intermedios o árboles de decisión (Brandao, Dyer y Hahn, 2005; Smith, 2005) (G. S. Milanesi, 2016). De igual manera, existe evidencia de aplicaciones que consideran momentos estocásticos de orden superior transformando la distribución binomial para incorporar asimetrías y curtosis en la proyección del recorrido aleatorio del subyacente (Rubinstein, 1998; Haahtela, 2010; Milanesi, 2012) (G. S. Milanesi, 2016) 

Dentro de las derivaciones y complementos al modelo de valoración de opciones mediante árboles binomiales está la propuesta de Smit y Trigeorgis (2004)(Cuervo, Felipe,. Botero, 2014), que combina teoría de juegos y de decisiones de inversión estratégica como opciones reales, modeladas mediante una malla binomial. El proceso se desarrolla en dos fases:

Figura 1
Distribución de probabilidades de activos futuro

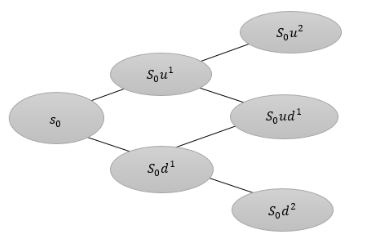
Fuente: Adaptada de (Vasseur & Pérez, 2016)

3.2   Modelos de Volatilidad

El Método del valor presente logarítmico de Copeland y Antikarov (2001) (Haque, Topal, & Lilford, 2014) es la primera explicación detallada del uso de la simulación Monte Carlo para la estimación de volatilidad basado en los flujos de efectivo. Este enfoque se basa en varios supuestos: en primer lugar, la renuncia de activos comercializados y prueba de Samuelson (1965)(Jaeck & Lautier, 2016) quien sostiene que la tasa estimada de retorno de cualquier activo sigue un paseo aleatorio independientemente del patrón de los flujos de efectivo. En segundo lugar, este proceso se basa en la idea de que una inversión con opciones reales debe valorarse como si fuera un activo que cotiza en los mercados, aunque no esté listado en bolsa. En tercer lugar, el valor presente de los flujos de efectivo del proyecto sin flexibilidad es la mejor estimación objetiva del valor de mercado del proyecto.

Un aporte complementario para la estimación de la volatilidad es propuesto por Brandão, Dyer y Hahn (2005)(González, G., Mora, A., y Solano, 2015), quienes sugiere una alternativa en la que el modelo de simulación de Copeland y Antikarov (2001)(Haque et al., 2014) se modifica dejando fijo el primer flujo de caja (FCF1) y los siguientes flujos de efectivo FCF2, ..., FCFN se especifican como valores esperados condicionales del resultado anterior.

En el mismo sentido, Godinho (2006) (Godinho; P, 2006) , inspirado por Longstaff y Schwartz (2001) (Fabozzi, Paletta, & Tunaru, 2017), Godinho (2006) (Godinho; P, 2006)  presentan el método de regresión de mínimos cuadrados para la estimación de la volatilidad. Este procedimiento consta de cuatro pasos: definir el número de trayectorias de muestreo, número de funciones básicas para la regresión, tipo de funciones básicas y número de observaciones.  Los autores señalan que si el número de trayectorias y el número de funciones son muy grandes el valor de la opción obtenido converge a un resultado teórico.

El enfoque de valoración neutral al riesgo generalizado, es otro método para encontrar la volatilidad. Se basa en los supuestos y las cualidades del Movimiento Browniano Geométrico (MBG) y en la distribución lognormal del activo subyacente. Una propuesta similar presenta Smith (2005) (Smith.J, 2005), quien sugiere que la parametrización correcta para el valor medio y la volatilidad se puede encontrar al cambiarlas, de tal forma que coincidan con los resultados simulados en el flujo de caja.  

El Método de mínimos cuadrados de regresión con enfoque neutral al riesgo de Haahtela (2010) (Haahtela, 2010) amplía aún más la idea de Godinho (2006) (Godinho; P, 2006) y las propiedades de valoración neutral al riesgo generalizada para la estimación de los cambios de volatilidades para diferentes periodos de tiempo. El enfoque utiliza mínimos cuadrados ordinarios para determinar el valor presente de los flujos de caja.

El análisis se desarrolla utilizando datos reales de una empresa multinacional que ejecuta proyectos de explotación minera en Colombia. Con los datos analizados y suministrados por los estudios de factibilidad técnica y económica de dicho proyecto se construyó el flujo de caja libre (ver Tabla 6)  (Arango, Mónica A; Montes, 2017)

Tabla 1
Resultado Flujo de caja libre

Fuente: elaboración de los autores

EL FCL se proyectó con los modelos econométricos estimados para describir el comportamiento del precio del oro. El VPN obtenido por el método clásico a una tasa de descuento del 8.04% fue de 89.675 kUSD  (Arango, Mónica A; Montes, 2017)

Los métodos tradicionales de evaluación de proyectos, no incorporan la flexibilidad de la toma de decisiones que en pueden modificar su valor. En este contexto, es necesario incorporar la metodología de Opciones de Reales como complemento a la valoración basados en flujos de caja.  El modelo parte de la idea de que a lo largo del tiempo el valor de un activo puede evolucionar con un aumento de valor o una disminución, de tal manera que su estimación consiste en adicionar el valor de la opción al valor presente del Flujo de Caja Libre.

La estimación de los parámetros de la opción es equivalente a los de las opciones financieras (ver Tabla 2 ).

Tabla 2
Parámetros para valorar la opción real

Fuente: Elaboración de los autores

En lo anterior se tiene en cuenta que el riesgo del mercado está implícito en la volatilidad del activo y de este depende su valor de subida y bajada, por lo tanto, el valor de este es independiente de las expectativas alcistas o bajistas que tenga el mercado sobre la evaluación de su rendimiento. En la Tabla 3  se encuentran los parámetros para la valoración.

Tabla 3
Datos para valoración

Fuente: elaboración de los autores

El valor del salvamento se estima en 74.202 k USD, es importante aclarar que este valor no se ajusta durante los años del proyecto, ya que los terrenos sufrirán un deterioro permanente a causa de la explotación del mineral. Además, no se desarrollará ningún tipo de actividad agrícola o ganadera, inclusive al final del proyecto deberá hacerse una inversión considerable para tratar de recuperarlo y dejarlo en condiciones óptimas.

El valor actual neto del proyecto se estima en 15.473 k USD, es decir, se recupera la inversión inicial de 74.202 k USD y queda una ganancia adicional de 15.473 k USD, este resultado se tiene en cuenta para la proyección del activo subyacente.

Ahora, se invertirá en el proyecto sólo si el valor esperado de este supera el monto de la inversión, en caso contrario se abandonara el proyecto y su valor pasara a ser cero en ese punto, en la Figura 2 se observa cómo se construye la proyección del activo subyacente y se realiza la aplicación.

Figura 2
Proyección del activo subyacente

Fuente: elaboración de los autores

En la Figura 3 se analiza la valoración de la opción, el reticulado tiene exactamente la misma cantidad de nodos y ramificaciones que el del activo subyacente. Se trabajó hacia atrás, desde los valores de los nodos terminales de la derecha a la izquierda del reticulado.

El valor colocado en cada nodo terminal es el máximo entre cero y la diferencia entre el valor  y el precio de ejercicio , La desaprobación de los valores negativos refleja el derecho del tomador de negarse a ejercer una opción con valor negativo (G. Milanesi, 2014). Si el valor del proyecto minero con la opción de abandono es igual a 58.728,40 k USD, y su valor sin contar con ella es de 15.473,60 k USD el valor de dicha opción de abandono será:

Figura 3
Valoración de la opción

Fuente: elaboración de los autores

El valor de decisión de abandonar será: OR: 1.049  KUSD + 163.877 KUSD = 164.926 KUSD.De tal manera que, si el valor actual de los costos de cierre y liquidación superase dicha cantidad, no interesaría liquidar el proyecto (al menos en los próximos ochos años, que se estima es la vida útil del proyecto).

Los tomadores de decisiones constantemente se enfrentan a escenarios cambiantes, que los incentivan a modificar las estrategias de inversión. De allí que, la metodología empleada para la valoración de los proyectos que desarrollarán sean fundamentales con el fin de contar con un punto de partida en futuras políticas empresariales, asociadas con la maximización de los beneficios.

De lo anterior, la herramienta de flujo de caja descontados tradicionalmente se ha empleado para dar soporta en el ámbito de la toma de decisiones. Sin embargo, requiere de un ajuste que considere la flexibilidad en las posibles trayectorias futuras, falencia que se convierte en un elemento notorio en el caso de los proyectos de inversión minero. En este sentido, se emplea como complemento la valoración a través de opciones reales.

Los resultados muestran que en los dos primeros años se da viabilidad para abandonar el proyecto. Sin embargo, pasado este periodo son más altas las posibilidades de pérdida si ejerce la opción de abandono, ya que se presentan escenarios en los cuales se recomienda continuar con el proyecto.

Arango, Mónica A; Montes, L. F. A. (2017). Aplicación de una opción real de abandono con simulación Monte Carlo y Volatilidad condicional GARCH : Un caso de estudio para un proyecto de inversión minera. Revista Espacios., 38(52), 22.

Arango, M. A. A., & Botero, S. B. (2017). The application of real options as a tool for decision-making in the electricity market [La aplicación de opciones reales como herramienta de toma de decisiones en el mercado de electricidad]. Iberian Conference on Information Systems and Technologies, CISTI. http://doi.org/10.23919/CISTI.2017.7975807

Bloomberg. (n.d.). Gold Spot $/OZ Curncy, en linea, disponible, acceso el 10 septiembre del 2015, datos tomados del 8 de septiembre del 2005 al 8 septiembre del 2015.

Cox, J., Ross, S., & Rubinstein, M. (1979). Option Pricing: A simplified approach. Journal of Financial Economics, 7(3), 229–263.

Cuervo, Felipe,. Botero, S. (2014). Aplicación de las opciones reales en la toma de decisiones en los mercados de electricidad. Estudios Gerenciales, 30(30), 397–407.

Fabozzi, F. J., Paletta, T., & Tunaru, R. (2017). An improved least squares Monte Carlo valuation method based on heteroscedasticity, 263, 698–706. http://doi.org/10.1016/j.ejor.2017.05.048

Godinho; P. (2006). Monte Carlo estimation of projet volatility for real option analysis. Journal of Applied Finance, 16(1), 15–30.

González, G., Mora, A., y Solano, G. (2015). empleando diferentes métodos de estimación de la volatilidad. Estudios Gerenciales, 31(136), 287–298. http://doi.org/10.1016/j.estger.2015.03.004

Guedes, J. (2017). The commodity super price cycle and real options: Implications for the Greeks of mining firms. Review of Financial Economics, 406, 11.

Haahtela, T. (2010). Displaced Diffusion Binomial Tree for Real Option Valuation. Aalto University, School of Science and Technology, 14–17.

Haque, M. A., Topal, E., & Lilford, E. (2014). A numerical study for a mining project using real options valuation under commodity price uncertainty. Resources Policy, 39(1), 115–123. http://doi.org/10.1016/j.resourpol.2013.12.004

Jaeck, E., & Lautier, D. (2016). Volatility in electricity derivative markets : The Samuelson effect revisited. Energy Economics, 59, 300–313. http://doi.org/10.1016/j.eneco.2016.08.009

Milanesi, G. (2014). Modelo binomial para la valoración de empresas y los efectos de la deuda : escudo fiscal y liquidación de la firma. Journal of Economics, Finance and Administrative Science, 19(36), 2–10. http://doi.org/10.1016/j.jefas.2014.03.004

Milanesi, G. S. (2016). El arrendamiento financiero y valuación de opciones reales. Contaduría Y Administración, 61(2), 353–373. http://doi.org/10.1016/j.cya.2015.11.010

Reboredo, J. C., & Ugolini, A. (2017). Quantile causality between gold commodity and gold stock prices. Resources Policy, 53(November 2016), 56–63. http://doi.org/10.1016/j.resourpol.2017.05.013

Smith.J. (2005). Alternative approach for solving real options problems. Decision Analysis, 2(2), 89–102.

Tanaka, Á. T., Marilia, C., & Montero, C. (2016). Valorización de opciones reales: modelo Ornstein-Uhlenbeck. Journal of Economics, Finance and Administrative Science, 1–7. http://doi.org/10.1016/j.jefas.2016.07.001

Trigeorgis, L., & Tsekrekos, A. E. (2018). Real Options in Operations Research: A Review. European Journal of Operational Research, 0, 1–24. http://doi.org/10.1016/j.ejor.2017.11.055

Vasseur, J. P., & Pérez, C. C. (2016). Valoración de patentes farmacéuticas a través de opciones reales : equivalentes de certeza y función de utilidad. Contaduría Y Administración, 61(4), 794–814. http://doi.org/10.1016/j.cya.2016.06.004

Este trabajo es producto de la Investigación para optar al Título de Magister en Finanzas de la Universidad de Medellín.

1. Profesora tiempo completo, Programa de Ingeniería Financiera, Universidad de Medellín y Docente Cátedra Universidad Nacional de Colombia. Economista, Universidad de Antioquia, Medellín, Colombia. Estudiante de doctorado en ingeniería industria y organizaciones, Universidad Nacional de Colombia. Magister en Administración financiera y magister en finanzas, universidad EAFIT, Medellín, Colombia. Profesora tiempo completo, Programa de Ingeniería Financiera, Universidad de Medellín, Medellín, Colombia. Miembro activo del grupo de investigación en ingeniería Financiera GINIF. Carrera 87 Nº 30-65, Medellín, Colombia. Teléfono +57(4)3405288. Correo electrónico: moarango@udem.edu.co

2. Profesor tiempo completo, Programa de Ingeniería Financiera, Universidad de Medellín, Medellín, Colombia. Ingeniero electricista, Universidad de Antioquia, Medellín, Colombia. Magister en Finanzas y magister en finanzas, Especialista en finanzas y mercado de capitales Universidad de Medellín, Medellín, Colombia.. Miembro activo del grupo de investigación en ingeniería Financiera GINIF. Carrera 87 Nº 30-65, Medellín, Colombia. Correo electrónico: lfmontes@udem.edu.co

3. Administrador de empresas, Fundación Universitaria Católica del Norte, Medellín, Colombia. Máster MBA Internacional en Administración y Dirección de empresas, Universidad Camilo José Cela y Bureau Veritas Business School, Madrid, España. Estudiante de Maestría Finanzas Universidad de Medellín, Medellín, Colombia. Docente cátedra tiempo completo de administración, Corporación Universitaria Minuto de Dios. Asesora empresarial, Servicio Nacional de Aprendizaje, SENA, Medellín, Colombia. Cra 28 nª 32-34. Teléfono. +57(4) 5760000. Correo electrónico: dcarboledag@misena.edu.co