ISSN 0798 1015

Vol. 39 (Nº 37) Año 2018 • Pág. 16

Modelo de Charles B. Nelson y Andrew F. Siegel para la estimación de la estructura temporal de tasas de interés

Nelson-Siegel model for estimation of term structure of interest rates

Juan Felipe BEDOYA Guisao 1; Luis Fernando MONTES Gómez 2; Horacio FERNÁNDEZ Castaño 3

Recibido: 27/03/2018 • Aprobado: 11/05/2018

Contenido

1. Introducción

2. Aspectos Generales

3. Metodología de estimación

4. Resultados

5. Conclusiones

Referencias bibliográficas

1. Introducción

La estructura temporal de tasas de interés, ETTI, es definida como la relación entre rendimientos y vencimientos de bonos cero cupón, entendiendo que el término “cero cupón” indica que dichos rendimientos se encuentran corregidos del efecto causado por el pago de cupones hasta el vencimiento. La ETTI ha sido objeto de estudio y evaluación durante años, y dicho proceso de investigación ha llevado a la creación de diversas metodologías de estimación que se encuentran fundamentadas en diversos criterios matemáticos y de mercado cuyo objeto es resolver, de manera óptima, los retos y limitaciones generados por la dinámica sistémica de los mercados financieros.

La estructura temporal de tipos de interés no solo ha experimentado cambios por la cantidad de metodologías desarrolladas para su estimación, sino que también ha sido merecedora del otorgamiento de una alta ponderación en la toma de decisiones por parte de autoridades monetarias e inversionistas, los cuales consideran que tomar como punto de referencia la información generada por dicha estructura podría minimizar la probabilidades de perdida en sus portafolios. Por lo anterior se han presentado diversos acontecimientos que no han hecho fácil el uso de esta estructura; uno de ellos y el más preponderante es la elección de una de las metodologías existentes para la estimación de una herramienta útil para la toma de decisiones, se ha tomado como criterio fundamental que dicha metodología debe ofrecer la mayor cantidad de criterios con los cuales se pueda realizar una estimación adecuada y cercana al contexto real del mercado.

Ya que existen múltiples metodologías para estimar la ETTI  que incorporan una gran cantidad de criterios matemáticos y de mercado que deben ser explicados y contextualizados de manera integral para obtener un adecuado entendimiento de los mismos, se enfatiza aquí sobre la metodología de mayor aceptación y utilización a nivel mundial , y es por ello que en el presente artículo se explicará y analizará el modelo propuesto y desarrollado por Nelson & Siegel (1985) , detallando, de la mejor manera, los criterios utilizados para su construcción  y evaluando matemáticamente su estructura,  y además buscando comprender de manera integral su alcance, trascendencia e importancia en los mercados financieros . Además se exponen algunas conclusiones en las cuales se enmarcan algunas ventajas y desventajas presentes en su aplicación.

La estructura temporal de las tasas de interés ha sido de gran importancia a través del tiempo tanto para inversionistas como para los principales responsables de la política monetaria a nivel mundial. Las decisiones que se toman con base en esta estructura impactan de manera directa aspectos como la valoración de activos, la gestión de portafolios y la evaluación de riesgos, es por ello que se hace necesario que la estimación de la misma sea realizada utilizando metodologías de ajuste que posean la capacidad de incorporar una alta cantidad  de factores influyentes en criterios tales como precisión y veracidad (Alfaro, Becerra, & Sagner, 2010).

La consideración de diversos factores influyentes en la ETTI, tiene por objetivo minimizar la posibilidad de obtener una ETTI no ajustada a la realidad de mercado, la cual impactaría de manera negativa a diversos agentes en los mercados financieros, además afectaría de forma directa la credibilidad de las valoraciones realizadas a diversos activos y las decisiones de política monetaria sustentadas en dicha estructura.

Es lo anterior lo que indujo a los economistas Nelson & Siegel (1985) a proponer una metodología que permitiera la estimación de una curva de rendimientos capáz de cumplir con criterios básicos tales como simplicidad, eficiencia y alto grado de ajuste.

El modelo propuesto por Nelson & Siegel (1985) surgió como respuesta a la necesidad explicita de estructurar una metodología que pudiera explicar de manera clara y sencilla el comportamiento de los rendimientos en el mercado de deuda, por supuesto estas consideraciones no fueron dadas sin argumentos ya que se había realizado un completo análisis de todos los modelos que, en su momento, eran reconocidos como los de mayor trascendencia técnica, y que de acuerdo con la percepción de Nelson y Siegel explicaban de mejor manera la relación entre niveles de tasas de interés y plazos al vencimiento.

Buscando entender de manera más precisa la estructura temporal de tasas de interés, Nelson y Siegel analizaron algunos modelos de alto reconocimiento técnico , entre los que se encuentran el  propuesto por (Durand, 1942) el cual de manera subjetiva buscaba encontrar una curva razonable que pudiera incorporar la mayor cantidad de puntos en la relación de rendimiento y plazo. (McCulloch, 1971)  propuso aproximar la función del valor actual a través de un spline definido en tramos mediante polinomios vinculados a los datos de los precios del instrumento, (Shea, 1984) demostró que la función de rendimiento tiende a doblarse bruscamente hacia el final del periodo de maduración, lo cual  parece ser más una  propiedad improbable que una verdadera relación con la curva de rendimiento. A estos modelos se le suman otros de carácter paramétrico relacionados con (Nelson & Siegel, 1985) y los propuestos por (Cohen, Kramer, y Waugh 1966); (Fisher 1966); (Echols & Elliott 1976); (Vasicek, 1977); (Dobson, 1978); y (las Salas, & Carleton Waldman 1984), aunque los modelos anteriores mantienen cierta consistencia con algunas ideas planteadas inicialmente por Charles B. Nelson y Andrew F. Siegel, relacionadas con la sencillez de su aplicación, es importante definir que para los modelos ya referenciados se hace necesario realizar procesos de extrapolación para períodos muy amplios lo cual le resta  precisión en el ajuste.

Además de los modelos basados en regresiones polinomiales, los autores Nelson y Siegel también identificaron modelos basados en splines exponenciales, los cuales buscaban ser una alternativa frente a los splines polinomiales. De estos se puede destacar el propuesto por (Vasicek & Fong, 1992), quienes argumentan que utilizando esta estructura se puede obtener una mejor condición de ajuste en la curva de rendimientos de los instrumentos de deuda , argumento que años atrás fue cuestionado por (Shea, 1984) , para quien esta metodología de ajuste presenta las mismas deficiencias técnicas que las encontradas en los splines polinomiales, las cuales se basan en la incapacidad para realizar predicciones extra muéstrales y en las grandes oscilaciones que genera sobre la curva forward.

Una vez observados algunos de los modelos referenciados anteriormente, Charles B. Nelson y Andrew F. Siegel llegaron a la conclusión de que era necesario proponer una metodología para la construcción de una curva de rendimiento fácilmente aplicable, que pudiera ser utilizada como herramienta de análisis en los mercados financieros, conceptualmente más satisfactoria que las propuestas planteadas hasta el momento a través de splines polinomiales y menos dependiente de los juicios subjetivos del observador (Nelson & Siegel, 1985).

El modelo propuesto por Charles B. Nelson y Andrew F. Siegel se basa en la solución de una ecuación diferencial ordinaria de segundo orden con raíces reales e iguales, la cual pertenece a las funciones conocidas como funciones de laguerre.(Berenguer, 2009) y (Universidad de Medelliín, 2008)

La solución correspondiente se concentra en la evolución de la tasa forward instantánea y no en la dinámica de la tasa corta, algo de suma importancia ya que la curva de rendimientos es obtenida mediante el promedio de la tasa forward instantánea y no como el promedio de la tasa corta (Arango, Fernando, & Mauricio, 2003).

2.1. Principios Estructurales del Modelo de Charles B. Nelson y Andrew F. Siegel

Las letras del tesoro son instrumentos de deuda de corto plazo que incorporan una promesa de pago en una fecha determinada, ya que no existen pagos intermedios hasta el vencimiento del título, su valor de mercado es inferior al valor facial establecido en las condiciones iniciales del título. La yield de estos títulos es definida como la tasa de retorno producida por el valor nominal de una inversión igual al precio de mercado, mantenida hasta la fecha de maduración.(Santana, 2008) y (Lizarzaburu & Barriga, 2016)

De acuerdo con (Ruiz. Dotras, 2005) y (González & Pérez, 2007), a través de la teoría de arbitraje se asegura que aquellas letras con la misma maduración tienen el mismo precio y por lo tanto mantienen la misma yield en cualquier instante del tiempo, situación que no se cumple si existe diferencia en la maduración de los títulos ya que  implicaría cambios de la yield en el mismo punto del tiempo, es así pues como en caso de contar con dos letras que mantienen períodos de maduración diferentes se hace necesario establecer la llamada forward yield  entre ambos períodos de maduración.

El modelo de (Nelson & Siegel, 1985) sostiene que si se tuvieran dos títulos con maduraciones diferentes, para el caso actual y  el inversionista podría evaluar la posibilidad de asegurar la tasa forward de retorno para el periodo  ya que  vendiendo los títulos con maduración en  y generando un reemplazo con los títulos de maduración en ,  esta situación dependería de la diferencia que pueda presentarse entre las tasas forward disponibles en el mercado y las expectativas que pudiera tener el inversionista sobre las tasas de retorno que probablemente pueda tener el mercado para el periodo lo cual indica la influencia de los expectativas sobre la estructura de mercado. Lo anterior también puede sugerir que las fluctuaciones de la tasa forward para maduraciones de muy largo plazo son bajas ya que las expectativas pudieran tener un mayor impacto en periodos de corto o mediano plazo.

Tomando en cuenta las consideraciones anteriores se establece que un modelo satisfactorio para la estructuración de la curva de rendimiento, debería cumplir con algunos elementos básicos tales como tasas forward suaves, es decir que puedan ser representadas mediante funciones diferenciables en todo punto de su dominio, y que además las oscilaciones que se presenten en esta función puedan ser amortiguadas, de manera que a largo plazo converjan a cero. Lo referenciado toma gran importancia para la construcción de la curva de rendimiento ya que las tasas al vencimiento podrían ser expresadas como la suavización de las tasas forward que intervienen en la estructura.

Con el fin de profundizar en la hipótesis descrita anteriormente y buscando entender de manera  estructural la relación entre maduración y tasas de interés, (Nelson & Siegel, 1985) tomaron información de cierre del mercado que incorporaba  las tasas de descuento directamente de la hoja de precios de la reserva federal con fecha del 22 de enero de 1981, a través de esta información pudieron identificar que las tasas experimentaban un aumento en función de la maduración hasta cerca de los 100 días, luego evidenciaron una disminución hasta cerca de los 300 días, en donde después de esto parecía nivelarse nuevamente. Estas apreciaciones fueron altamente valoradas para la estructuración del modelo ya que permitieron entender que la relación de las tasas de interés frente a la maduración de los títulos no mantenía necesariamente una tendencia creciente a medida que aumentaba el tiempo, de igual manera se pudo establecer que la función necesaria para las condiciones que planteaba el mercado debía incorporar la capacidad de elevarse a un nivel máximo para después caer monótonamente hacia un valor asintótico.

Los polinomios no cumplían con las condiciones establecidas para la función de ajuste, ya que estos forman fácilmente una figura de joroba que no se instala en un valor asintótico, por el contrario tiende a tomar valores hacia más o menos infinito, la única forma de poder considerar una función  de este tipo era realizar  la elección de un polinomio muy específico, el cual debía poseer un grado lo suficientemente alto con lo cual se pudiera obtener una curva que se aproxime a los puntos de los datos base, es decir un polinomio de grado igual al número de puntos presentes en los datos menos uno, con lo cual pueda ser construida una curva que coincida exactamente con cada punto. La función en si misma exhibió fluctuaciones agresivas entre los puntos de la información base, con lo cual se estableció que los rendimientos de las letras del tesoro que se encontraban cercanos unos de los otros mantenían una condición no causal ya que se trataban de títulos muy específicos emitidos por la reserva federal.

Para dar solución a las altas fluctuaciones evidenciadas en el polinomio propuesto anteriormente, se consideró la utilización de splines, para lo cual se hace necesario el uso  de polinomios de bajo grado que pudieran adaptarse a los diferentes plazos de maduración  en esencia se trataba de los planteamientos generados por (McCulloch, 1971), aunque mantenía diferencias ya que McCulloch estructuró los splines con precios y no con rendimientos. Además de estas diferencias era claro que se mantenía cierta resistencia hacia los splines polinomiales ya que se consideraba como un enfoque que no lograba solucionar la deficiencia fundamental de los polinomios, y se sostenía que su pendiente tiende a aumentar de manera absoluta a medida que se tienen maduraciones más grandes. Otras dificultadas identificadas en este caso por (Shea, 1984) definían que aunque la curva generada pudiera ser razonable con gran parte de las maduraciones,  las tasas forward implícitas describían comportamientos erráticos en el extremo superior de la serie, fue entonces cuando Charles B. Nelson y Andrew F. Siegel expresan de manera directa la intención de desarrollar un modelo que incorpore intrínsecamente la suavidad y la amortiguación asintótica que permita la generación, a priori, de curvas de rendimiento y tasas forward implícitas, seguido a esta manifestación, el interés de calcular el rendimiento que se puede esperar a los 360 días para una letra del tesoro, si el único rendimiento observado tan solo se encuentra disponible hasta los 330 días.

Fue esta la idea que permitió entender que los splines polinomiales no cumplían con las exigencias del modelo que se pretendía plantear, ya que este tipo de funciones no cuentan con los criterios necesarios para realizar una predicción extra muéstral, y en cambio se opta por utilizar una clase de modelo compuesto por la solución de una ecuación en diferencias finitas no homogénea de segundo orden con coeficientes constantes, dada por:

2.2. Modelación de la dinámica de la Tasa Forward

La tasa forward instantánea será definida como

(Zuñiga & Soria, 1999) destacan que el desarrollo anterior confirma que la curva de rendimiento no es más que el promedio de los valores futuros de la tasa forward instantánea.

2.3. Tasa de Interés Spot

La flexibilidad del modelo permite que a partir de la función que expresa la tasa forward se pueda determinar la función que describe la tasa spot, para la cual solo es necesario realizar un proceso de integración a la función de la tasa forward (González & Pérez, 2007).

3. Metodología de estimación 

Para la estimación de las curvas spot diarias calculadas entre el 24/07/2016 y  24/08/2016 se tomaron las tasas diarias de cierre de los títulos de renta fija con los siguientes vencimientos 24/10/2018, 11/09/2019, 24/07/2020, 04/05/2022, 24/07/2024 y 26/08/2026, dentro de los títulos mencionados anteriormente  no se relacionan las siguientes referencias vinculadas a la curva de rentabilidad de TES tasa fija ( 04/2028 , 09/2030 y 07/2032), dichas referencias no fueron consideradas ya que de acuerdo con el análisis realizado , el cual tomó como base de evaluación  los criterios de liquidez y volumen de negociación, estas referencias no vinculaban en su momento las condiciones necesarias para hacer parte de la ETTI propuesta, y por ende su aporte no era significativo. Toda la información fue evaluada directamente en el sistema de información de la BVC.

 Igualmente se debe  considerar que el mercado de renta fija colombiano se encuentra altamente  rezagado con relación a mercados como el chileno y el peruano, el número de referencias disponibles es altamente limitado y del total de las referencias existentes solo unos pocos títulos mantienen condiciones aceptables en términos de volumen de negociación y liquidez, dicha situación limita la amplitud y profundidad del mercado.

Para los días en los cuales el mercado tuvo poco movimiento y las referencias objeto de estudio no presenta tasas de cierre, se toma como dato base la última tasa de cierre reportada.

En el momento en que se tenga la observación y la estimación para cada una de las referencias diarias de mercado, es necesario calcular la diferencia entre ambas y el resultado deberá ser elevado al cuadrado. Este procedimiento deberá ser aplicado para cada una de las referencias. Una vez se tengan las 6 diferencias que para el caso actual fue el número de referencias consideradas, las mismas deberán ser sumadas y su resultado se convierte en la función objetivo relacionada a continuación:

4. Resultados

Los resultados obtenidos,  muestran las tasas estimadas para los tres primeros y los últimos tres días de la muestra total de 32 días, es decir, la estructura temporal de tipo de interés obtenida para los días 24/07/2016  25/07/2016, 26/07/2016, 22/08/2016, 23/08/2016, 24/08/2016, y  correspondiente  a las referencias  24/10/2018, 11/09/2019, 24/07/2020, 04/05/2022, 24/07/2024 y 26/08/2026.

Tabla 1
Relación de Tasas de Interés y Vencimientos

-----

Tabla 2
Parámetros de Estimación

El primer cuadro referencia las estructura temporal de tipos de interés obtenida para 6 de los 32 días, allí se pueden establecer plazos de estimación de entre 1 y 6 años, el segundo cuadro incorpora los parámetros de referencia utilizados para realizar la estimación  a través del modelo de Nelson Y Siegel , el valor de se obtuvo minimizando la suma de los cuadrados de los errores MSE, con lo anterior se reduce la diferencia entre las observaciones realizadas en el mercado de renta fija colombiano y respectiva estimación, dicha minimización se realiza con la herramienta de optimización presente en Excel.

La representación gráfica de cada uno de las estructuras temporales de tipo de interés se relaciona a continuación:                             

Gráfica 1
Curva de rendimientos estimada con = 1.14847432

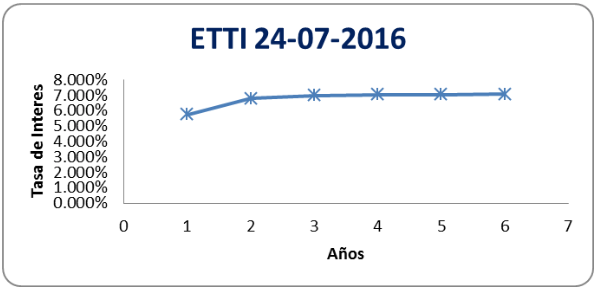
Fuente: elaboración propia

------

Gráfica 2
Curva de rendimientos estimada con = 1.14881788

Fuente: elaboración propia

-----

Gráfica 3
Curva de rendimientos estimada con = 1.14902255

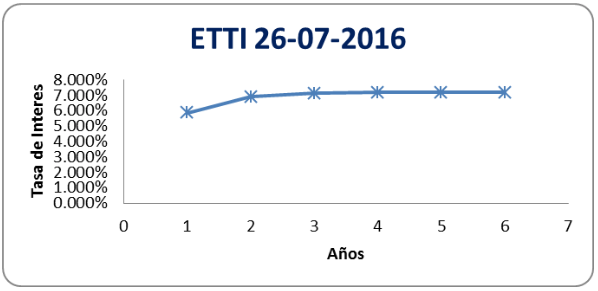
Fuente: elaboración propia

-----

Gráfica 4
Curva de rendimientos estimada con = 1.15855308

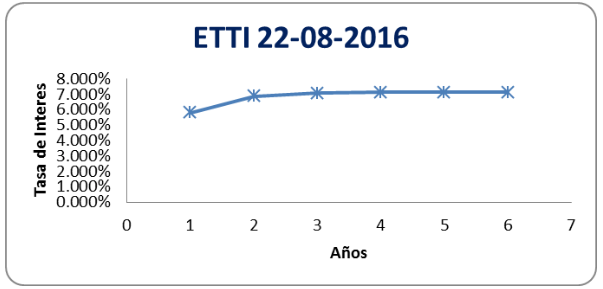
Fuente: elaboración propia

-----

Gráfica 5
Curva de rendimientos estimada con = 1.15891971

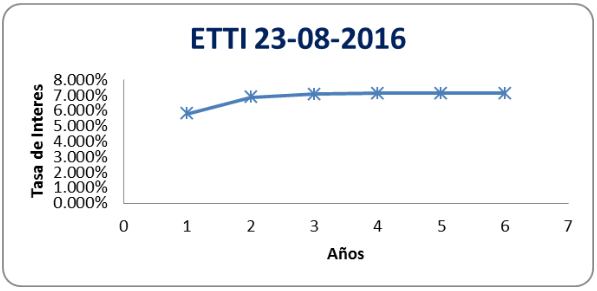
Fuente: elaboración propia

-----

Gráfica 6
Curva de rendimientos estimada con = 1.15933925

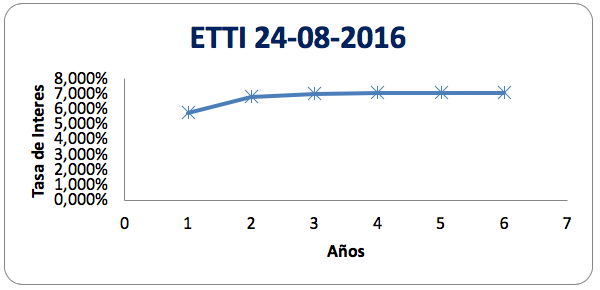
Fuente: elaboración propia

Tomando como base  el día  24/07/2016 se cambiaron los valores de Tau, con el objeto de observar el  impacto de este parámetro en la estimación de la estructura temporal de tipos de interés, a continuación se presentan los resultados obtenidos.

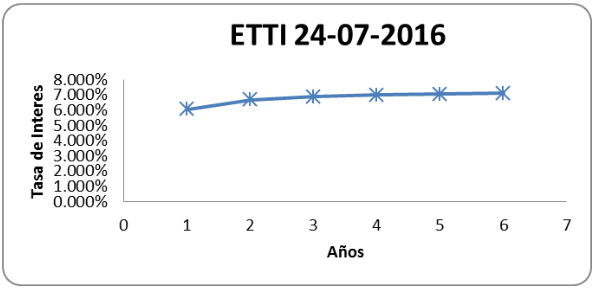
Gráfica 7
Curva de rendimientos estimada con = 1.14847432

Fuente: elaboración propia

----- 

Gráfica 8
Curva de rendimientos estimada con = 30.5657

Fuente: elaboración propia

Los resultados obtenidos demuestran de forma preliminar que un aumento en el valor de genera un cambio en  la curva de corto plazo, este cambio es evidente al comparar las tres estructuras de tipo de interés  y al identificar que el ajuste de la curva de largo plazo no cambia significativamente. Dicho lo anterior se hace importante reconocer la relevancia de obtener un Tau adecuado que permita la generación de una estructura de tipo de interés equilibrada la cual pueda evitar  descompensaciones tanto en la curva de corto plazo como  en la curva de largo plazo.

La eficiencia y precisión del modelo de Nelson y Siegel depende de manera importante de una fuente de datos lo suficientemente robusta, la cual permita realizar estimaciones integrales, que incorporen comportamientos generales de mercado y de esta manera servir como elemento de base para la toma de decisiones. El caso colombiano demuestra que el mercado de renta fija aún se encuentra en desarrollo y que la información relevante se concentra en pocos títulos, esta situación afecta de manera directa la posibilidad de que el modelo de Nelson y Siegel pueda tener un alcance mayor del que actualmente posee en nuestro mercado.

Reconocer la importancia del parámetro  y de la metodología utilizada para su respectivo cálculo, permite tener confiabilidad en la precisión y la eficiencia del modelo de Nelson y Siegel, obviar lo anterior y no otorgar la relevancia requerida a este elemento, generaría constantes distorsiones predictivas y restaría confiabilidad a la hora de tomar decisiones con base en la ETTI obtenida mediante esta metodología de estimación.

Aunque el modelo de Nelson y Siegel es un modelo parsimonioso de fácil entendimiento y aplicación, podría no ser adecuado para estructuras temporales de tipos de interés que incorporen alta complejidad (altos niveles de incertidumbre), en dicho caso, su utilización podría generar condiciones de sobrestimación que afectarían de manera directa la confiabilidad de la respectiva ETTI. En lo anterior se coincide con (Avendaño, Cariaga, & Martinez, 2007) los cuales proponen modelos alternativos como el propuesto por (Lars. E. O, 1994) o (Vasicek & Fong, 1992).

El modelo de Nelson y Siegel, se constituye entonces como uno de los modelos más utilizados a nivel mundial por múltiples autoridades monetarias, pues su simplicidad y bondad de ajuste proporciona estructuras temporales de tipos de interés con un alto nivel de flexibilidad. El complemento generado por el modelo de Svensson potencializó el reconocimiento del modelo original y ha generalizado su uso durante los últimos 20 años. Tanto ha sido del impacto de dicho modelo que de acuerdo con lo estipulado por (González & Cecilia, 2015) el mismo es utilizado por las autoridades monetarias de países como Bélgica, Finlandia, Francia, Alemania , Italia , Noruega,  España y Suiza.  

Alfaro, R., Becerra, S., & Sagner, A. (2010). Estimación de la Estructura de Tasas Utilizando el Modelo Dinámico Nelson Siegel: Resultados para Chile y EEUU. doi:10.5897/JAERD12.088

Arango, L., Fernando, L., & Mauricio, D. (2003). “Estimación de la Estructura a Plazo de las Tasas de Interés en Colombia.” Coyuntura Economica, Fedesarrolo.

Avendaño, F., Cariaga, J., & Martinez, R. (2007). Construcción De Curvas Cero Cupon Para Bonos Chilenos. Universidad de Chile.

Berenguer, E. (2009). La Estimación de la Estrucutura Temporal de los Tipos de Interes:Metodología y Aplicaciones.

Durand, D. (1942). Basic yields of corporate bonds, 1900-1942. Basic yields of corporate bonds, 1900-1942 (Vol. I, pp. 1–40). Retrieved from http://www.nber.org/chapters/c9268.pdf

González, M., & Cecilia, M. (2015). interés : una aplicación al cálculo de riesgo de tasas de interés.

González, M., & Pérez, M. (2007). Una Estimación de la Estructura de Tasas de Interés.

Lars. E. O, S. (1994). Estimating and Interpreting Forward Interest Rates: Sweden 1992-1994.

Lizarzaburu, R., & Barriga, G. (2016). Una herramienta de financiamiento gubernamental: El Programa de Creadores de Mercado y Mercado de Bonos en el Perú. Revista Espacios, 37.

Maldonado, R., Zapata, N., & Pantoja, J. (2012). Estimación Dinámica de una Estructura de Tasas de Interés Para Colombia. Análisis Empírico con Filtros de Kalman.

McCulloch, H. (1971). Measuring The Term Structure of Interest Rates. The Journal of Business, 44, 19–31. doi:10.1086/295329

Nelson, C. B., & Siegel, A. F. (1985). Parsimoneus Modeling Of Yield Curves For U.S Treasury Bills.

Ruiz. Dotras, E. (2005). Comparación de Curvas de Interés. Efectos de la Integración Financiera.

Santana, J. (2008). La Curva De Rendimientos:Una Revisión Metodológica y Nuevas Aproximaciones De Estimación. Cuadernos de Economia.

Shea, G. S. (1984). Pitfalls in Smoothing Interest Rate Term Structure Data: Equilibrium Models and Spline Approximations. Journal of Financial and Quantitative Analysis, 253–259.

Universidad de Medelliín. (2008). Riesgos Financieros y Económicos (Fernández , Vol. 1, pp. 114–117). Medellín. doi:10.1017/CBO9781107415324.004

Vasicek, O. (1977). An Equilibrium Characterization Of The Term Structure. Journal of Financial Economics, 5, 177–188. doi:10.1016/0304-405X(77)90016-2

Vasicek, O., & Fong, H. (1992). Term Structure Modeling Using Exponential Splines. The Journal of Finance, 339–348.

Venegas, F. (2008). El Modelo de Nelson y Siegel. In Cengage Learning Editores (Ed.), Riesgos Financieros y Económicos (pp. 647–648–649). Mexico.

Zuñiga, S., & Soria, K. (1999). Estimación de la Estrucutura Temporal de Tasas de Interés en Chile, 1994-1997. Estudios de Administración, 6.

1. Maestrando, Facultad de Ingenierías, Maestría en Finanzas, Universidad de Medellín, Medellín, Colombia.             Analista de Beneficios Pensionales, Protección S.A,  Medellín, Colombia. jfbedoya@proteccion.com.co

2. Ingeniero Electricista, Universidad de Antioquia. Magister en Finanzas y Especialista en Finanzas y Mercado de Capitales, Universidad de Medellín. Profesor Tiempo Completo Programa de Ingeniería Financiera, Universidad de Medellín, Medellín, Colombia. Miembro Activo del Grupo de Investigación en Ingeniería Financiera GINIF Carrera 87 Nº 30-65, Medellín, Colombia. lfmontes@udem.edu.co

3. Ingeniero Civil, Escuela de Ingeniería de Antioquia. Magister en Matemáticas Aplicadas Universidad EAFIT Especialista en Sistemas de Administración de la Calidad, Universidad de Medellín, Especialista en Gerencia de Construcciones, Universidad de Medellín. Licenciado en Matemáticas, Universidad de Medellín. Profesor Tiempo Completo, Programa de Ingeniería Financiera, Universidad de Medellín, Medellín, Colombia. Miembro Activo del Grupo de Investigación en Ingeniería Financiera GINIF. Carrera 87 Nº 30-65, Medellín, Colombia. hfernsez@udem.edu.co