ISSN 0798 1015

Vol. 39 (Nº 37) Año 2018 • Pág. 9

Incidencia de los factores espaciales en la eficiencia de la dimensión salud del índice de desarrollo humano en México, 1990-2015

Incidence of spatial factors in the efficiency of the health dimension of the human development index in Mexico, 1990-2015

Francisco Javier AYVAR-CAMPOS 1; José César Lenin NAVARRO-CHÁVEZ 2; Víctor Manuel GIMÉNEZ-GARCÍA 3

Recibido: 23/03/2018 • Aprobado: 01/05/2018

Contenido

1. Introducción

2. Metodología

3. Resultados

4. Conclusiones

Referencias bibliográficas

1. Introducción

Se concibe al desarrollo humano como el proceso por el cual se expanden las opciones, oportunidades y el bienestar del individuo (McGillivray & White, 1993; Harttgen & Klasen, 2012). En la medición del concepto destaca el Índice de Desarrollo Humano (IDH), elaborado por el Programa de Naciones Unidas para el Desarrollo (PNUD). El IDH considera tres dimensiones: el ingreso, la salud y la educación (Alkire, 2002). Debido a sus características técnicas el IDH es el indicador sintético más aplicado en la medición del desarrollo humano y el bienestar social (PNUD, 2017a).

Los indicadores de salud en México, durante el período 1990–2015, tuvieron variaciones positivas que permitieron que el índice de salud del IDH tuviera un crecimiento del 9.5% (INEGI, 2017; Secretaría de Salud, 2017a, 2017b). De las tres dimensiones que componen el IDH, es la dimensión salud la que más incidió positivamente en el comportamiento del IDH nacional, durante el período de estudio (PNUD, 2017b). Sin embargo, el comportamiento de las variables de mortalidad, pobreza e inequidad revelan que aún se requieren mayores esfuerzos en la dimensión salud del desarrollo humano en México (CONEVAL, 2017a, 2017b; Secretaría de Salud, 2017a). La incidencia que tiene la salud en el desarrollo humano es directa, ya que de fortalecer el estado de salud de la población se fomenta el crecimiento económico y el bienestar social (London et al., 2009; Monterubbianesi, 2014).

La presente investigación analiza la incidencia de los factores espaciales en la eficiencia de la dimensión salud del IDH en los 32 estados de México, durante el período 1990–2015. La herramienta que se utilizó para medir la eficiencia técnica fue el Análisis de la Envolvente de Datos (DEA, por sus siglas en inglés). Se considera un Modelo DEA con orientación al output, estructurado bajo rendimientos variables a escala, con la presencia de bad outputs e incluyendo la incidencia de factores no controlables. Se tiene como output a la esperanza de vida al nacer; como bad output la carencia por acceso a los servicios de salud; como inputs controlables la cantidad de médicos y el número de unidades médicas disponibles; y, como input no controlable el coeficiente de Gini. Por otro lado, para determinar la influencia de los factores espaciales sobre los resultados de eficiencia se empleó la Econometría Espacial (EE). Se trabaja un modelo de correlación espacial mediante la aproximación de máxima verosimilitud. Siendo la variable dependiente de este modelo de regresión el promedio de los resultados de eficiencia, y las variables independientes el promedio de deuda pública y el grado promedio de escolaridad, del período 1990–2015.

El artículo se encuentra estructurado en tres apartados, en el primero, se presentan los elementos teórico-metodológicos de los modelos DEA y EE, así como el proceso y definición de las variables para cada uno de ellos. En el segundo apartado, se muestran los resultados de la eficiencia y de la incidencia espacial. Finalmente, se establecen las conclusiones del estudio.

En este apartado se presentan los rasgos teórico-metodológicos del modelo eficiencia, considerando la presencia de bad outputs y la incidencia de factores no controlables. De igual manera, se abordan los elementos teóricos-metodológicos del modelo de econometría espacial, desarrollado a fin de identificar la influencia de los factores espaciales en la eficiencia.

2.1. El análisis de la envolvente de datos

La conceptualización de eficiencia de Farrell (1957), se aplica empíricamente mediante la estimación de fronteras estocásticas y el Análisis de la Envolvente de Datos. DEA es una técnica aplicada en la cuantificación de la eficiencia de agentes homogéneos o Unidades de Toma de Decisión (DMU, por sus siglas en inglés). Partiendo de los inputs y outputs, este método proporciona una clasificación de las DMU, otorgándoles una puntuación de eficiencia relativa. Es así, como aprovechando el know how de las DMU eficientes, realiza un análisis de slacks estableciendo las mejoras que requieren las DMUconsideradas como ineficientes. A su vez, los modelos DEA pueden ser elaborados con Rendimientos Constantes a Escala (CRS, por sus siglas en inglés), Rendimientos Variables a Escala (VRS, por sus siglas en inglés), aditivos y multiplicativos. De igual forma, es factible que tengan dos orientaciones, hacia la combinación optima de inputs o hacia la optimización de la producción de outputs (Cooper et al., 2007). Sin embargo, salidas indeseables (bad outputs) se producen a menudo conjuntamente con resultados deseables (outputs). En este sentido, Pittman (1983) introdujo el tratamiento de los bad outputs dentro de los análisis DEA. El resultado de este nuevo enfoque permite deducir una medida de eficiencia en la cual, con orientación al output, busque maximizar la salida de los good outputs y a la par minimizar los bad outputs (Seiford & Zhu, 2002).

Gran parte de las investigaciones basadas en el DEA se focalizan en el análisis de la gestión de los productores; sin considerar la influencia de los factores exógenos al proceso de producción, pero que inciden en la generación de outputs. La inclusión de estos factores no controlables permite que los resultados de eficiencia muestren si el productor clasificado como ineficiente lo es realmente o si aun haciendo todo lo que está en su mano, hay factores que le imposibilitan lograr la producción que otros si obtienen (Cordero et al., 2005). Recientemente diversos estudios incorporan en las mediciones de eficiencia (DEA) a las variables no controlables, estableciendo así distintas propuestas metodológicas. A fin de simplificar la presentación de estas alternativas metodológicas se han conformado tres categorías, como son (Cordero et al., 2005): a) Modelos de Separación de Frontera, b) Modelos de Una Etapa, y c) Modelos de Varias Etapas. Los Modelos de Varias Etapas, a su vez, se pueden subdividir en dos grupos, que son: a) Modelos de Segunda Etapa, y b) Modelos de Valores Ajustados. Derivándose de estos últimos los Modelos de Tres Etapas, y los Modelos de Cuatro Etapas.

2.2. El modelo DEA considerando bad outputs y factores no controlables

Con la intención de incorporar la incidencia de los factores no controlables en la eficiencia se desarrolló un modelo de cuatro etapas, considerando la presencia de bad outputs. Es así como, partiendo de los postulados de Cordero et al. (2005), el modelo se elaboró de la siguiente manera (Ayvar-Campos et al., 2017):

El output del modelo de eficiencia fue la esperanza de vida al nacer y el bad output la población con carencia de acceso al sistema de salud, la razón de haberlos retomados es por la representatividad teórica que tienen para explicar el bienestar social. La selección de inputs controlables y no controlables se fundamentó, en primera instancia, en las bases teóricas que explican el comportamiento de la dimensión salud del IDH (Kirigia et al., 2004; Nevárez-Sida et al., 2007; Mirzosaid, 2011; De Nicola et al., 2012; Iñiguez et al., 2012; Hadad et al., 2013; Varabyova & Schreyögg, 2013; Asandului et al., 2014; Cheng & Zervopoulos, 2014; Davutyan & Bilsel, 2014; Cordero et al., 2016; Jakovljevic et al., 2016). Debido a las limitaciones de información en las bases estadísticas oficiales del país el número de inputs se redujo. Con los indicadores restantes se aplicó un análisis factorial, para cada tipo de input (controlable y no controlable), empleando como método de extracción los componentes principales. A partir de los resultados de la matriz de componentes se determinó que los inputs controlables del modelo de eficiencia serían los médicos y las unidades médicas disponibles; y el input no controlable sería el coeficiente de Gini (Ver Tabla 1).

Tabla 1
Variables del modelo DEA de cuatro etapas

Fuente: Elaboración propia.

2.3. La econometría espacial

El desarrollo de la ciencia regional planteó la necesidad de diferenciar la economía tradicional de la economía espacial o regional, así como también de disociar los instrumentos que se utilizan para tal fin. Este proceso de distinción ha sido permanente, ya que desde sus orígenes el análisis regional destaca la importancia de establecer marcos analíticos regionales integrados que permitan sintetizar las diferentes herramientas y técnicas vinculadas a subsistemas regionales bajo un mismo marco teórico (Isard, 1960; Meyer, 1965). En esta evolución se han elaborado diversos trabajos que estiman y evalúan a la región bajo modelos econométricos (econometría espacial multirregional y modelos de econometría e insumo producto). La Econometría Espacial (EE) se presenta así como una opción a la econometría estándar para tratar con datos referenciados espacialmente y contrastar fenómenos económicos (Paelinck & Klaassen, 1979). De esta forma, y de acuerdo con Anselin (1988) la EE es “la colección de técnicas que tratan con las peculiaridades causadas por el espacio en el análisis estadístico de los modelos de la ciencia regional” (Moreno y Vayá, 2002, p. 2).

La EE reconoce dos tipos de efectos espaciales: la heterogeneidad y la dependencia espacial (Anselin & Florax, 1995). El primer efecto aparece cuando se utilizan datos de unidades espaciales muy distintas para explicar un mismo fenómeno. En este caso, aparecen problemas como la heterocedasticidad o la inestabilidad estructural, los cuales pueden ser resueltos mediante las técnicas econométricas existentes para series temporales. Por otro lado, la dependencia o autocorrelación espacial surge siempre que el valor de una variable en un lugar del espacio está relacionado con su valor en otro u otros lugares del espacio. La dependencia espacial no puede ser tratada con econometría estándar, debido a la multidireccionalidad que denomina las relaciones de interdependencia entre unidades espaciales, por lo que se utiliza la EE (Moreno y Vayá, 2000, 2002).

2.4. Rasgos del modelo de la econometría espacial

Tabla 2
Variables del modelo de econometría espacial

Fuente: Elaboración propia.

3. Resultados

En este apartado se muestran los resultados obtenidos de los modelos DEA y EE. Para tal fin, en primera instancia se analizan los resultados de eficiencia, y posteriormente se exponen los resultados del modelo espacial.

3.1. Análisis de la eficiencia técnica de gestión con bad outputs

Los estados considerados como eficientes durante el período 1990-2015, en la utilización de sus recursos (médicos y unidades médicas disponibles) para generar bienestar en salud (esperanza de vida al nacer) y reducir la inequidad (carencia de acceso al sistema de salud), sustrayendo la incidencia de los factores no controlables (coeficiente de Gini), fueron Baja California Sur, Quintana Roo y Colima. Mientras que en algunos años se destacaron por ser eficientes Aguascalientes, Baja California Norte, Distrito Federal y Yucatán. Por otro lado, las entidades más ineficientes durante el período analizado fueron Chiapas, Chihuahua, Guerrero, Oaxaca y Veracruz. Ello implica que estos estados no utilizaron de manera eficiente sus recursos en el período estudiado, para generar bienestar en salud y reducir la inequidad (Ver Tabla 3).

Tabla 3
Resultado del modelo DEA de cuatro etapas

Fuente: Elaboración propia con base en datos de la Secretaría de Salud (2017a, 2017b),
CONEVAL (2017a, 2017b), e INEGI (2017); y, utilizando los programas SPSS, Eviews y MaxDea.

3.2. Determinación de la incidencia de los factores espaciales sobre la eficiencia

El AEDE de contraste global permitió identificar la existencia de una autocorrelación espacial positiva en la variable dependiente, con una I de Moran de 0.7170. Estos resultados ponen de manifiesto que la evolución de la distribución de la eficiencia en salud se ha producido de forma agrupada en el espacio. Lo que implica que los estados con valores de eficiencia relativamente altos/bajos tienden a estar rodeados de entidades con valores de eficiencia similares. Es decir, los resultados de eficiencia no son observaciones independientes, sino que están influenciadas por el espacio (Ver Figura 1). Por su parte el AEDE de contraste local (LISA) identifica la existencia de un clúster regional significativo de valores altos de eficiencia en salud entre Jalisco, Aguascalientes, Zacatecas y Coahuila, así como entre Quintana Roo y Yucatán; y de valores bajos de eficiencia entre Guerrero, Oaxaca, Chiapas y Veracruz (Ver Figura 2). Asociaciones espaciales que corresponden con el desempeño de sus indicadores socioeconómicos y de sus niveles de bienestar social (CONEVAL, 2017a, 2017b; INEGI, 2017; PNUD, 2017b; Secretaría de Salud, 2017a, 2017b; SEP, 2017; SHCP, 2017).

Figura 1
Diagrama de dispersión de moran y mapas de eficiencia 1990–2015

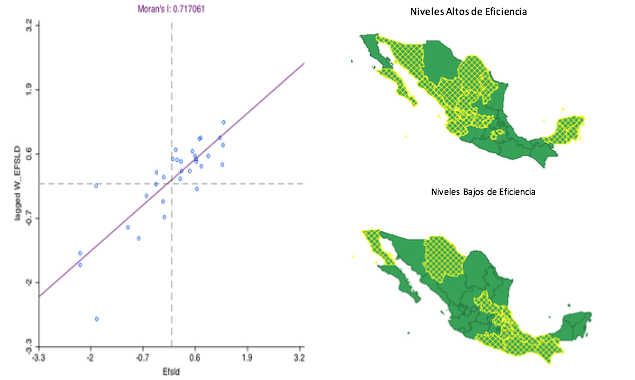
Fuente: Elaboración propia con base en datos de la Secretaría de Salud (2017a, 2017b),
CONEVAL (2017a, 2017b), INEGI (2017), SEP (2017) y SHCP (2017); y, utilizando el programa GeoDa.

-----

Figura 2
Mapas Lisa de agrupamiento de la eficiencia 1990–2015

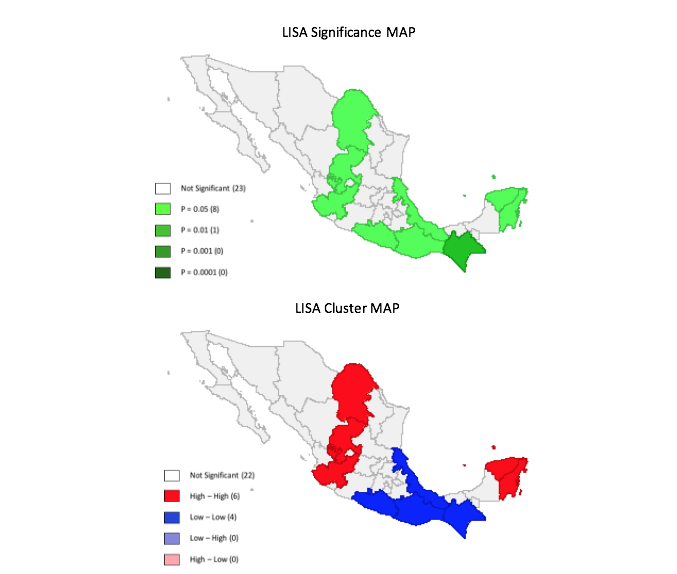
Fuente: Elaboración propia con base en datos de la Secretaría de Salud (2017a, 2017b),
CONEVAL (2017a, 2017b), INEGI (2017), SEP (2017) y SHCP (2017); y, utilizando el programa GeoDa.

Una vez detectada la existencia de autocorrelación espacial fue necesario realizar la estimación de MCO del modelo y analizar la existencia de efectos espaciales. De esta forma, en la Tabla 4 es posible observar que los resultados del modelo de regresión espacial con MCO muestran que existe una correlación espacial positiva entre la variable dependiente (eficiencia en salud) y las variables independientes (niveles de deuda pública y grado promedio de escolaridad) con una I de Moran de 2.5981, y una probabilidad de 0.0937. Conviene subrayar que el ajuste del modelo MCO es alto ya que: las variables explicativas son significativas, se puede aceptar la hipótesis de homocedasticidad y de normalidad, y no existen problemas de multicolinealidad. Así mismo, los resultados del test Lagrange Multiplier (error) son mayores que el de Lagrange Multiplier (lag) en las diferentes especificaciones, lo que siguiere que el modelo debe reespecificarse incluyendo un retardo espacial en el error. Esto se debe a la posible omisión de variables no cruciales para el modelo pero que podrían encontrarse correlacionadas espacialmente con la variable dependiente.

Tabla 4
Modelo espacial con mínimos cuadrados ordinarios

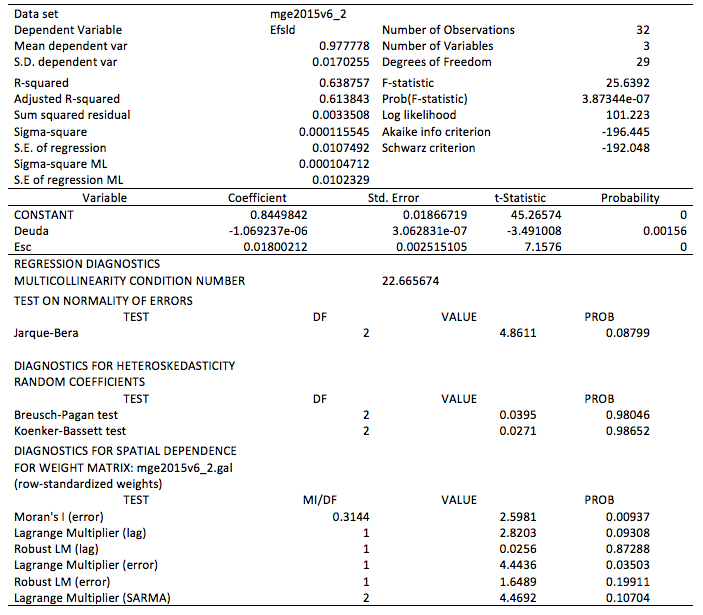
Fuente: Elaboración propia con base en datos de la Secretaría de Salud (2017a, 2017b),
CONEVAL (2017a, 2017b), INEGI (2017), SEP (2017) y SHCP (2017); y, utilizando el programa GeoDa.

La estimación del modelo espacial con retardo en el error se efectuó mediante la aproximación de Máxima Verosimilitud (MV). En la Tabla 5 del anexo se observa que bajo este esquema se obtiene un modelo econométrico con una R cuadrada de 0.700594; un test de Breusch-Pagan de 0.0088 con una probabilidad de 0.9956; y, un test de Lakelihood Ratio de 4.2313 con una probabilidad de 0.03969. Datos que dan cuenta de la viabilidad estadística del modelo espacial, y que prueban la relación de dependencia espacial entre la variable dependiente y las independientes. Es a partir de estos resultados, que se argumenta que el uso eficiente de los recursos de los estados mexicanos durante el período 1990–2015, para generar bienestar en salud y a la par reducir la inequidad, restando la incidencia de factores no controlables, estuvo influenciado por la proximidad geográfica a entidades con altos grados promedio de escolaridad y bajos niveles de deuda. Lo que implica que la eficiencia depende tanto de la gestión de los recursos como de factores espaciales, argumento que concuerda con los postulados de Schaffer et al. (2011), Liu et al. (2014), Sun et al. (2014), Adetutu et al. (2015), Guan y Xu (2016), y Vidoli y Canello (2016).

Tabla 5
Modelo espacial bajo máximo verosímil residual

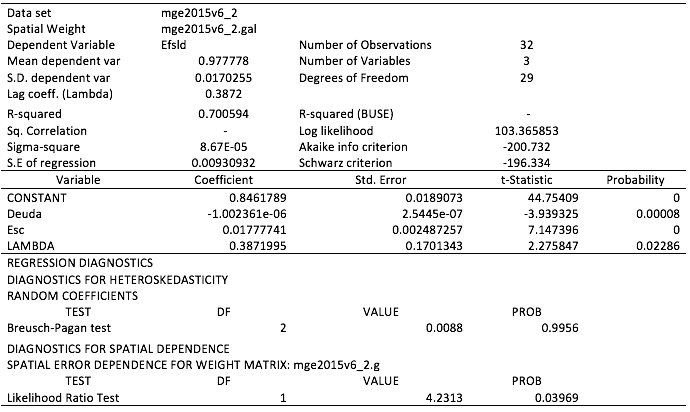
Fuente: Elaboración propia con base en datos de la Secretaría de Salud (2017a, 2017b),
CONEVAL (2017a, 2017b), INEGI (2017), SEP (2017) y SHCP (2017); y utilizando el programa GeoDa.

La presente investigación constituye un aporte empírico al análisis de los determinantes espaciales de la eficiencia en la generación de bienestar en salud y en la reducción de la inequidad en al acceso al servicio de salud. El objetivo fue determinar la incidencia de los factores espaciales en la eficiencia de la dimensión salud del IDH en México, durante el período 1990–2015. Para esto, se consideraron los postulados teórico–metodológicos de los Modelos de Cuatro Etapas del DEA con la presencia de bad outputs y de autocorrelación espacial de los modelos de EE.

El Modelo del DEA de Cuatro Etapas fue diseñado con orientación al output, estructurado bajo rendimientos variables, con la existencia de bad outputs y la incidencia de factores no controlables. Se tiene entonces como output la esperanza de vida al nacer; como bad output la carencia de acceso a los servicios de salud; como inputs controlables la cantidad de médicos y el número de unidades médicas disponibles; y, como input no controlable el coeficiente de Gini. La finalidad de este modelo fue la de obtener una medida de eficiencia técnica de gestión que refleje el uso eficiente de los recursos en la generación de bienestar en salud y en la reducción de la inequidad.

Para identificar la incidencia de los factores espaciales sobre los niveles de eficiencia se elaboró un modelo de correlación espacial. Este modelo partió del establecimiento de una matriz de pesos, basada en una contigüidad tipo Queen y de primer orden; de la definición del operador del retardo espacial; de la aplicación del AEDE; de la elaboración del modelo de MCO; y de la aplicación del modelo MV. La variable dependiente del modelo de EE fue el valor promedio de los resultados de eficiencia del modelo DEA; y, las variables independientes fueron el promedio de deuda pública y el grado promedio de escolaridad del período 1990–2015.

Los resultados obtenidos del modelo DEA muestran que durante el período 1990–2015 los estados de Baja California Sur, de Quintana Roo y de Colima tuvieron los mayores niveles de eficiencia. Es decir, fueron las entidades que hicieron el mejor uso de sus recursos (médicos y unidades médicas disponibles) para generar bienestar en salud (esperanza de vida al nacer) y reducir la inequidad (carencia de acceso al servicio de salud), sustrayendo la incidencia de los factores no controlables (coeficiente de Gini). Resultados que dejan ver que los estados que más percibieron recursos en la dimensión salud del IDH (Distrito Federal, el Estado de México, Jalisco, Guanajuato, Nuevo León, Puebla, Baja California, Tamaulipas y Veracruz) no siempre fueron los más eficientes.

En los resultados del modelo de EE se observa que el uso eficiente de los recursos de los estados mexicanos durante el período 1990–2015, para generar bienestar en salud y a la par reducir la inequidad, restando la incidencia de factores no controlables, estuvo influenciada por la proximidad geográfica a entidades con altos grados promedio de escolaridad y bajos niveles de deuda. Esta información hace evidente la necesidad de una gestión más adecuada de los recursos; y que el desempeño adecuado en áreas económicas y sociales ajenas a las variables propias de la dimensión salud del IDH en los estados vecinos favorecen la eficiencia. Lo que implica el desarrollo de políticas públicas focalizadas por entidad federativa que fomenten el uso eficiente de los recursos, y la generación de clústeres espaciales que fortalezcan el bienestar social.

Adetutu, M., Glass, A. J., Kenjegalieva, K., & Sickles, R. C. (2015). The effects of efficiency and TFP growth on pollution in Europe: a multistage spatial analysis. Journal of Productivity Analysis, 43(3), 307–326. http://doi.org/10.1007/s11123-014-0426-7

Alkire, S. (2002). Dimensions of human development. World Development, 30(2), 181–205. http://doi.org/10.1016/S0305-750X(01)00109-7

Álvarez Castaño, L. S. (2009). Los determinantes sociales de la salud: Más allá de los factores de riesgo. Revista Gerencia y Politicas de Salud, 8(17), 69–79.

Anselin, L. (1988). Spatial Econometrics: Methods and Models (1 st. ed., Vol. 4). Amsterdam, Netherlands: Springer. http://doi.org/10.1007/978-94-015-7799-1

Anselin, L., & Florax, R. (1995). New Directions in Spatial Econometrics. (1 st. ed.). Berlin, Heidelberg: Springer. http://doi.org/10.1007/978-3-642-79877-1

Anselin, L., & Rey, S. J. (2014). Modern Spatial Econometrics In Practice: A guide to GeoDa, GeoDaSpace and PySAL (1st. ed.). Chicago, IL., USA: GeoDa Press.

Asandului, L., Roman, M., & Fatulescu, P. (2014). The Efficiency of Healthcare Systems in Europe: A Data Envelopment Analysis Approach. Procedia Economics and Finance, 10, 261–268. http://doi.org/10.1016/S2212-5671(14)00301-3

Ayvar-Campos, F. J., Navarro-Chávez, J. C. L., y Giménez-García, V. M. (2017). La eficiencia de la dimensión ingreso del IDH en México The Efficiency of the Income Dimension of the HDI in Mexico Información del artículo Resumen. Ensayos Revista de Economía, 36(362), 95–122.

Barahona-Urbina, P. (2011). Factores determinantes de la esperanza de vida en Chile. Anales de La Facultad de Medicina, 72(4), 255–259.

Cardona, D., Acosta, L. D., y Bertone, C. L. (2013). Inequidad en salud entre países de Latinoamérica y el Caribe (2005-2010). Gaceta Sanitaria, 27(4), 292–297. http://doi.org/10.1016/j.gaceta.2012.12.007

Cheng, G., & Zervopoulos, P. D. (2014). Estimating the technical efficiency of health care systems: A cross-country comparison using the directional distance function. European Journal of Operational Research, 238(3), 899–910. http://doi.org/10.1016/j.ejor.2014.05.007

CONEVAL. (2017a). Evolución de Dimensiones de la Pobreza. Recuperado el 24 de Abril de 2017 de http://www.coneval.org.mx/Medicion/EDP/Paginas/Datos-del-Modulo-de-Condiciones-Socioeconomicas.aspx

CONEVAL. (2017b). Informe de Pobreza en México 2014. Recuperado el 24 de Abril de 2017 de http://www.coneval.org.mx/InformesPublicaciones/Documents/Informe-pobreza-Mexico-2014.pdf

Cooper, W. W., Seiford, L. M., & Tone, K. (2007). Data Envelopment Analysis. A Comprehensive Text with Models, Applications, References and DEA-Solver Software (2nd ed.). New York, USA: Springer Science & Business Media. http://doi.org/10.1007/978-0-387-45283-8

Cordero, J. M., Nuño-Solinís, R., Orueta, J. F., Polo, C., del Río-Cámara, M., y Alonso-Morán, E. (2016). Evaluación de la eficiencia técnica de la atención primaria pública en el País Vasco, 2010-2013. Gaceta Sanitaria, 30(2), 104–109. http://doi.org/10.1016/j.gaceta.2015.11.002

Cordero Ferrera, J. M., Pedraja Chaparro, F., y Salinas Jiménez, J. (2005). Eficiencia en educación secundaria e inputs no controlables: Sensibilidad de los resultados ante modelos alternativos. Hacienda Pública Española, 2(173), 61–83.

Davutyan, N., & Bilsel, M. (2014). Efficiency of Turkish Provincial General Hospitals with Mortality as Undesirable Output. In I. H. Osman, A. L. Anouze, & A. Emrouznejad (Eds.), Handbook of Research on Strategic Performance Management and Measurement Using Data Envelopment Analysis (1st. ed., pp. 426–436). Hershey, USA: ALMOS.

De Nicola, A., Gitto, S., & Mancuso, P. (2012). Uncover the predictive structure of healthcare efficiency applying a bootstrapped data envelopment analysis. Expert Systems with Applications, 39(12), 10495–10499. http://doi.org/0.1016/j.eswa.2012.02.074

Farrell, M. J. (1957). The measurement of productive efficiency. Journal of the Royal Statistical Society. Series A (General), 120(3), 253–290. http://doi.org/10.2307/2343100

Fried, H. O., Schmidt, S. S., & Yaisawarng, S. (1999). Incorporating the operating environment into a nonparametric measure of technical efficiency. Journal of Productivity Analysis, 12(3), 249–267. http://doi.org/10.1023/A:1007800306752

Guan, W., & Xu, S. (2016). Study of spatial patterns and spatial effects of energy eco-efficiency in China. Journal of Geographical Sciences, 26(9), 1362–1376. http://doi.org/10.1007/s11442-016-1332-x

Hadad, S., Hadad, Y., & Simon-Tuval, T. (2013). Determinants of healthcare system’s efficiency in OECD countries. The European Journal of Health Economics, 14(2), 253–265. http://doi.org/10.1007/s10198-011-0366-3

Harttgen, K., & Klasen, S. (2012). A household-based human development index. World Development, 40(5), 878–899. http://doi.org/10.1016/j.worlddev.2011.09.011

Idrovo, Á. J. (2005). Desigualdad en el ingreso, corrupción y esperanza de vida al nacer en México. Revista de Salud Pública, 7(2), 121–129.

INEGI. (2017). Número de médicos en instituciones públicas de salud en contacto con el paciente. Recuperado el 26 de Abril de 2017 de http://www3.inegi.org.mx/sistemas/cni/seriesestadisticas.aspx?idOrden=1.1&IndBase=6200009719*6300000266&indCve=6200009720&gen=595&d=n

Iñiguez, P. A., Ferreyra, E. L., Arburua, M., Hernández, M. S., y Iñiguez, A. L. (2012). La eficiencia del sistema de salud en las provincias. Un análisis con variables discrecionales y no discrecionales. Cuadernos Del CIMBAGE, 14(1), 73–87.

Isard, W. (1960). Methods of Regional Analysis: An introduction to regional science. (W. Isard, D. F. Bramhall, G. A. P. Carrothers, J. H. Cumberland, L. N. Moses, D. O. Price, & E. W. Schooler, Eds.) (1 st. ed.). Cambridge, Massachusetts: The M.I.T. Press.

Jakovljevic, M. B., Vukovic, M., & Fontanesi, J. (2016). Life expectancy and health expenditure evolution in Eastern Europe—DiD and DEA analysis. Expert Review of Pharmacoeconomics & Outcomes Research, 16(4), 537–546. http://doi.org/10.1586/14737167.2016.1125293

Kirigia, J. M., Emrouznejad, A., Sambo, L. G., Munguti, N., & Liambila, W. (2004). Using Data Envelopment Analysis to Measure the Technical Efficiency of Public Health Centers in Kenya. Journal of Medical Systems, 28(2), 155–166. http://doi.org/10.1023/B:JOMS.0000023298.31972.c9

Liu, B., Wang, X., & Huo, T. (2014). Spatial Econometric Analysis of the Energy Efficiency of the Chinese Regional Construction Industry. In J. Wang, Z. Ding, L. Zou, & J. Zuo (Eds.), Proceedings of the 17th International Symposium on Advancement of Construction Management and Real Estate (1st. ed., pp. 697–708). Berlin, Heidelberg: Springer Berlin Heidelberg. http://doi.org/10.1007/978-3-642-35548-6_72

London, S., Temporelli, K., y Monterubbianesi, P. D. (2009). Vinculación entre salud, ingreso y educación: Un análisis comparativo para América Latina. Economía Y Sociedad, XIV(23), 125–146.

McGillivray, M., & White, H. (1993). Measuring development? The UNDP’s Human Development Index. Journal of International Development, 5(2), 183–192. http://doi.org/10.1002/jid.3380050210

Meyer, J. R. (1965). Regional Economics: A Survey. In American Economic Association (Ed.), Surveys of Economic Theory Vol. II (1 st., pp. 240–271). London, U. K.: Palgrave Macmillan UK.

Mirzosaid, S. (2011). Health Expenditure Efficiency in the Commonwealth of Independent States: A Data Envelopment Analysis Approach. Transition Studies Review, 18(2), 384–404. http://doi.org/10.1007/s11300-011-0204-4

Monterubbianesi, P. D. (2014). El rol de la salud en el proceso de crecimiento económico: una revisión de la literatura. Cuadernos de Economía, 33(62), 91–121. http://doi.org/10.15446/cuad.econ.v33n62.43667

Moreno Serrano, R., y Vayá Valcarce, E. (2000). Técnicas econométricas para el tratamiento de datos espaciales: La econometría espacial (1 st.). Barcelona, España: Edicions de la Universitat de Barcelona.

Moreno Serrano, R., y Vayá Valcarce, E. (2002). Econometría espacial: nuevas técnicas para el análisis regional. Una aplicación a las regiones europeas. Investigaciones Regionales, 1, 83–106.

Nevárez-Sida, A., Constantino-Casas, P., y García-Contreras, F. (2007). Comparación de la eficiencia técnica de los sistemas de salud en países pertenecientes a la OMS. Economía, Sociedad Y Territorio, VI(24), 1071–1090.

Paelinck, J. H. P., & Klaassen, L. H. (1979). Spatial Econometrics (1 st.). Farnborough: Saxon House.

Pinzón Florez, C. E., Reveiz, L., Idrovo, A. J., y Reyes Morales, H. (2014). Gasto en salud, la desigualdad en el ingreso y el índice de marginación en el sistema de salud de México. Revista Panamericana de Salud Pública, 35(1), 1–7.

Pittman, R. W. (1983). Multilateral productivity comparisons with undesirable outputs. The Economic Journal, 93(372), 883–891. http://doi.org/10.2307/2232753

PNUD. (2017a). Human Development Data (1990-2015). Recuperado el 3 de Mayo de 2017 de http://hdr.undp.org/en/data

PNUD. (2017b). Sobre el desarrollo humano. Recuperado el 15 de Febrero de 2017 de http://hdr.undp.org/es/content/sobre-el-desarrollo-humano

Schaffer, A., Simar, L., & Rauland, J. (2011). Decomposing regional efficiency. Journal of Regional Science, 51(5), 931–947. http://doi.org/10.1111/j.1467-9787.2011.00731.x

Secretaría de Salud. (2017a). Cubo Dinámico. Recuperado el 24 de Abril de 2017 de http://www.dgis.salud.gob.mx/contenidos/basesdedatos/bdc_recursos_gobmx.html

Secretaría de Salud. (2017b). Esperanza de Vida al Nacer por Entidad Federativa. Recuperado el 24 de Abril de 2017 de http://www.dgis.salud.gob.mx/contenidos/sinais/indica_gral_gobmx.html

Seiford, L. M., & Zhu, J. (2002). Modeling undesirable factors in efficiency evaluation. European Journal of Operational Research, 142(1), 16–20. http://doi.org/10.1016/S0377-2217(01)00293-4

SEP. (2017). Indicadores y Pronósticos Educativos. Recuperado el 25 de Abril de 2017 de http://www.snie.sep.gob.mx/indicadores_pronosticos.html

SHCP. (2017). Indicadores de Obligaciones de Entidades Federativas y Municipios 2015. Recuperado el 25 de Abril de 2017 de http://obligaciones_entidades.hacienda.gob.mx/es/OBLIGACIONES_ENTIDADES/2015

Sueyoshi, T., & Goto, M. (2010). Should the US clean air act include CO2 emission control?: Examination by data envelopment analysis. Energy Policy, 38(10), 5902–5911. http://doi.org/10.1016/j.enpol.2010.05.044

Sun, C., Zhao, L., Zou, W., & Zheng, D. (2014). Water resource utilization efficiency and spatial spillover effects in China. Journal of Geographical Sciences, 24(5), 771–788. http://doi.org/10.1007/s11442-014-1119-x

Varabyova, Y., & Schreyögg, J. (2013). International comparisons of the technical efficiency of the hospital sector: Panel data analysis of OECD countries using parametric and non-parametric approaches. Health Policy, 112(1–2), 70–79. http://doi.org/10.1016/j.healthpol.2013.03.003

Vidoli, F., & Canello, J. (2016). Controlling for spatial heterogeneity in nonparametric efficiency models: An empirical proposal. European Journal of Operational Research, 249(2), 771–783. http://doi.org/10.1016/j.ejor.2015.10.050

Wang, K., Yu, S., & Zhang, W. (2013). China’s regional energy and environmental efficiency: A DEA window analysis based dynamic evaluation. Mathematical and Computer Modelling, 58(5–6), 1117–1127. http://doi.org/10.1016/j.mcm.2011.11.067

1. Profesor-Investigador. Instituto de Investigaciones Económicas y Empresariales. Universidad Michoacana de San Nicolás de Hidalgo. Doctor en Ciencias del Desarrollo Regional por la UMSNH. fayvar@umich.mx

2. Profesor-Investigador. Instituto de Investigaciones Económicas y Empresariales. Universidad Michoacana de San Nicolás de Hidalgo. Doctor en Ciencias del Desarrollo Regional por la UMSNH. cesar126@hotmail.com

3. Profesor-Investigador. Departamento de Empresa. Universidad Autónoma de Barcelona. Doctor en Ciencias Económicas y Empresariales por la UAB. victor.gimenez@uab.cat