ISSN 0798 1015

Vol. 39 (Number 30) Year 2018. Page 25

Interactive teaching as an effective method of pedagogical interaction

La enseñanza interactiva como método efectivo de interacción pedagógica

Marina V. VINOGRADOVA 1; Lyubov I. YAKOBYUK 2; Natalia V. ZENINA 3

Received: 04/04/2018 • Approved: 15/05/2018

Contents

1. Introduction

2. Materials and Methods

3. Results

4. Conclusion

Bibliographic references

1. Introduction

Intensive informatization of all fields of human activity puts new demands on higher vocational education, namely, the preparation of a competitive highly qualified specialist. In this regard, innovative methods and technologies of education should be aimed at raising students' creativity and initiatives. To achieve this goal, it is necessary to activate and methodically ensure contact communicative and independent work of students, which will allow adapting it to the dynamically changing reality. In the educational process, it is necessary to increase the role of seminars, workshops, laboratory works, colloquiums and other forms of active classroom and extracurricular activities for students. A special form of organization of cognitive activity is interactive education, on the basis of which the student, acquiring knowledge and skills, thereby creates a basis for work on solving problems after the end of education (Tsisar & Shalashnikova, 2012).

The study of psycho-pedagogical literature showed that the problems of interactive learning were considered by such scientists as Yu.G.Odegov (Odegov and Volgin, 2004), N.A. Volgin, A.I. Sidorenko (Sidorenko, 2011), Yu.P. Surmin (Surmin, 2002), G.S. Kharkhanova (Kharhanova, 1999), and others.

The word "Interactive" is formed from the word "Interact" (English), where "inter" means mutual, "act" means to act. The name of the method comes from the psychological term "interaction", which means "intercommunication". Interactionism is a trend in modern social psychology and pedagogy, based on the concepts of American sociologist and psychologist J. G. Mead. Interaction is understood as direct interpersonal communication, the most important feature that recognizes the ability of a person to "take on the role of another", to imagine how the communication partner or group perceives it, and accordingly interpret the situation and develop their own actions.

Interactive process is a thoughtful process of communication and interaction between participants in the educational process. The basis of this cooperation is the personal experience of each participant. The interactive process is characterized by a high intensity of communication, interaction and exchange of activities, change and variety of activities, processability (the condition for changing the status of participants), focused reflection by participants in their activities and interaction.

The meaning of interactivity is formed from the definition of the concepts "inter" (between) and "activity" (enhanced activity). In this connection, the term "interactive communication" can be interpreted as an intensified activity of participants in communication with each other, and the term "interactive pedagogical communication" - as an intensified, purposeful activity of the teacher and student in organizing interaction among them for development) (Zenina, 2012).

Along with the notions of "interactive process" and "interactive communication", such a concept as "interactive learning" is considered. Interactive learning is learning immersed in communication. Here, "immersed" does not mean "replaced". Interactive learning supports the ultimate goal and main content of the learning process. It modifies forms from translating into interactive ones, that is, it includes the exchange of information on the basis of mutual understanding and interaction.

Interactive learning is a special form of organization of cognitive activity, a method of cognition implemented in the form of joint activities of students, in which all participants interact with each other, exchange information, jointly solve problems, simulate situations, evaluate the actions of others and their own behavior, immerse themselves in real atmosphere of business cooperation to solve the problem.

It is possible to demonstrate the distinctive features of interactive learning in the following way (Figure 1):

Figure 1
Methods of interaction between the teacher and students

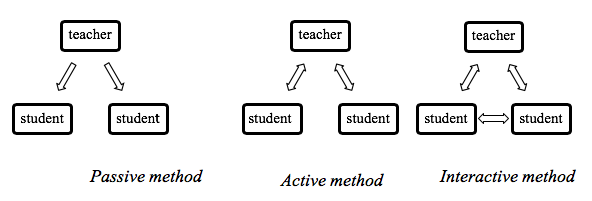
The essence of interactive learning "is to create didactic and psychological conditions that contribute to the manifestation of intellectual, personal and social activity of students" (Vinogradova, 2014b).

Therefore, the implementation of interactive forms of education is one of the most important areas of modern vocational education. Now it is not enough for a teacher to be competent in his field and transfer a huge base of knowledge to the audience. The use of active approaches is the most effective way to help students learn.

In the process of learning, it is necessary, first of all, to pay attention to those methods in which students identify themselves with educational material, join the studied situation, are encouraged to act, worry of the status of success and motivate their behavior. All these requirements are best suited for interactive learning methods.

The learning process, based on the use of interactive teaching methods, is organized taking into account participation in the learning process of all students in the group, without exception. Joint activity means that each contributes to learning in a special way - it is the exchange of knowledge, ideas, and ways of working. It can be organized both individually and in pairs, in the form of group work, using project work, role play, work with documents and various sources of information. Interactive methods are based on the principles of interaction and activity of students. An environment of educational communication is created that is characterized by openness, interaction of students, equality of their argumentations, accumulation of joint knowledge, possibility of mutual evaluation and control.

A leading teacher in the process of knowledge transfer leads the participants to self-examination. Vigorous activity of the teacher gives way to the activity of students, its goal is to create conditions for their initiative. The teacher refuses the role of a filter that conducts educational information through himself and serves as an assistant in the work, one of the sources of information. Therefore, interactive learning is intended initially for use in intensive student training.

Despite the relevance of these studies on the issue, it is not enough to focus on the development and implementation of examples of the use of interactive forms in the teaching of mathematics in the university.

The study, which is the first stage of the experiment, was conducted on the basis of the FSBEI of HE "Northern Trans-Ural State Agricultural University" in 2017. The study involved 211 students of the first and second year. As research methods were used the following: analysis of psychological, educational and methodological literature on the research topic, as well as comparison and generalization of the content of concepts and categories; comparative analysis of learning results; qualitative and quantitative analysis of the data; methods of statistical data processing.

In modern pedagogical literature, there are three types of interactivity in the learning process:

1. Interaction of the student and the subject of study. This type of interactivity determines the process of intellectual interaction of the student with the subject, leading to a change in the level of student preparation, and its intellectual development.

2. Interaction between the student and the teacher. The teacher creates motivation for learning, offering the student a certain material for information, demonstrating the application of modeling skills to a specific situation (task).

3. The interaction of students. This type of interactivity involves the interaction of students among themselves, an individual student with other students in the group, in the presence of the teacher or without him in real time (Vinogradova, 2014b).

Currently, there is no single generally accepted classification of interactive teaching methods in pedagogics. As a basis, we will use a more complete classification:

1) non-simulation, that is, used in the framework of traditional forms of educational activity, for example, lectures (problematic, with planned errors, case studies, etc.), practical exercises, course and graduation projecting, etc.;

2) simulation (game and non-game), which is associated with the use of new teaching methods in the educational process, for example, brainstorming, aquarium, training, case tasks, business game, discussion, etc.;

 3) webinar, online seminar (lecture, conversation) in synchronous mode, allowing listeners to actively participate in the learning process through questions, expression of opinion, communication with all participants. This is the so-called online training: the teacher conducts the seminar, the computer with the web camera broadcasts it, the online audience watches the seminar, listens and asks questions on the air. After the end of the event, a record remains, which can also be used for educational purposes. However, this distance education can not replace full-fledged education, because the emotional component, that occurs at the moment of the direct contact between the teacher and the audience, is lost. Therefore, the webinar is one of the forms of distance learning (Odegov and Volgin, 2004).

Consider the most frequently occurring interactive forms of giving math classes, and give examples of scenarios for some of them.

1) A problem lecture begins with the statement of the problem, which must be solved in the course of the presentation of the material. There is no ready solution in this case. That is, the student's activity is coming to the search and research ones. On such lectures, a dialogue between the teacher and students is required. Students actively participate in the discussion and search for certain solutions. This approach can be used actively when presenting applied chapters of mathematics, statistics, modeling methods.

2) Lecture-visualization teaches the student to convert oral and written information into a visual form, highlighting the most significant and essential elements. The lecture uses diagrams, figures, drawings, etc., made with the help of students. The teacher reduces giving the lecture to a coherent detailed commenting of the prepared visual aids. At the same time, the logic and rhythm of the teaching material is important. This type of lecture is good to use at the stage of introducing students into a new section, topic, or discipline. Visual presentation of the material helps to develop a clearer understanding of most of sections of the mathematics, modeling courses.

3) Lecture with pre-planned errors that students should find. The most common mistakes that both students and teachers make during lectures are selected. During the lecture, students should find mistakes and write them down in the abstract. At the end of the lecture, the mistakes are "declassified" and discussed. The method is used to describe the main theoretical moments (errors in the proof of theorems, basic properties, etc. are allowed).

Example. The topic of the lesson is "Method of integration by parts in an indefinite integral"

Number of planned errors – (7-8).  

Aim: to increase the attention of listeners, to involve them into the process of learning the material and to motivate the study of the discipline "Mathematics".

Tasks:

•   to interest students in the process of getting knowledge of the calculation of an indefinite integral;

•   To involve listeners into the process of discussing the obtained knowledge to search for the declared errors;

•   development of communication skills (social skills);

•   removal of psychological and physical stress in class.

Preparatory stage

In the previous lesson, the topic of the next lesson is announced, the number of expected errors and materials (or references to sources) are given for preliminary acquaintance with the stated topic.

Questions for preparing for the lecture:

1.  The concept of a primitive function and an indefinite integral;

2.  The derivative and integral of the basic elementary functions;

3.  Differential of a function;

4.  Properties of the indefinite integral.

5.  Integration methods: direct integration, method of changing a variable.

Suggested reading:

1. Bavrin I.I. Higher mathematics. - M.: Publishing Center "Academy", 2007. - 616 p.

2. Vilenkin I.V., Grober V.M. Higher mathematics for students of economic, technical, natural-science majors of universities. - 5th ed. - Rostov-on-Don: Phoenix, 2009 - 521p.

3. Danko P.E., Popov A.G. Higher mathematics in exercises and problems in 2 parts: a textbook for high schools / P.E. Danko, A.G. Popov - 5th ed., corrected. M.: Higher School, 2003 - 304 p.

Introduction (10 min).

1. The teacher informs about the purpose, tasks and method of the lecture, about the tasks of the students at the lecture, and also about the fact that the student can get points for active participation in the lecture.

2. The teacher announces the topic of the lecture and the approximate number of planned errors.

 The lecture is held in the form of a PPT-presentation, its material is divided into three sections:

•   The derivation of the integration formula by parts in an indefinite integral (the number of planned errors is 1).

•   The scheme of finding the indefinite integral by the formula of integration by parts (the number of planned errors is 3-4).

•   Use of the formula of integration by parts in the return integral (the number of planned errors is 1-2).

     Types of errors:

•   Mathematical - "random" errors in mathematical relations and expressions.

•   Logical - errors in the configuration of mathematical schemes and formulas.

The main part (65 min). The material of the lecture is presented in the form of three blocks, after each of which students were offered for 5-7 minutes of time for discussion and searching for block errors.

In fact, the material presented contains 7 errors. They include:

1. In the first block, there are errors in differentiation in the derivation of the formula of integration by parts;

2. In the second block - an incorrect partition of the integrand (1 error). Incorrect finding of derivative, integral in the selected functions u and dv, errors in algebraic calculations. (3 errors).

3. In the third block, an incorrect definition of the integration method (1 error). Errors in finding the integral, which must be integrated in parts several times (1 error).

Conclusions (reflection) (15 minutes).

During this time, students should express their opinion on the results of the search for errors.

The teacher should evaluate the level of preparation of students on this topic and put scores to active students.

4) Lecture with the analysis of a specific situation, stated orally or in the form of a short filmstrip, video recording, etc.; students jointly analyze and discuss the represented material. The method is convenient for studying applied disciplines (mathematical statistics, mathematical modeling, game theory, economic statistics, econometrics). Thus, for the teacher who lectures, the function of direct transmission of information should be transformed into the function of organizing the student's independent work to master this academic discipline.

5) Contextual education (refers to non-game simulation methods) is aimed at forming an integral model of the future professional activity of the student. At the same time, knowledge and skills are given not as a subject for memorization, but as a means of solving professional problems. Applied in the teaching of applied aspects of mathematics, methods of mathematical modeling, statistics, econometrics. Actively used when working with students in economic specialties.

6) Method for the group solution of creative tasks helps to choose the best one from the proposed series of alternative variants: members of the group are required to evaluate each variant in a certain sequence. It is very convenient for the construction and evaluation of mathematical models of real situations in economics, engineering practice. Also, using this method, we can note the following relations of the learning process: student-student (develops the ability to build relationships among peers, the ability to argue reasonably for their point of view, the ability to respond quickly to emerging comments and questions, broadens the horizon), student-teacher (learning process occurs on an individual basis using feedback). Thus, all the possibilities of an interactive approach to learning are revealed.

Example. Practical lesson on the topic "The formula of total probability. Bayes' formula"

The aim of the lesson: To generalize and systematize the students' knowledge on the given topic.

Tasks:

•   development of skills in the group communication and interaction;

•   formation of value-orientation unity of the group.

Preliminary preparation. The teacher gives each student an individual task on the topic "The formula of total probability. Bayes' formula" before the lesson, which they must solve by this lesson. Each task is numbered from 1 to 6. The teacher introduces the students to the plan of the lesson, with the rules of their behavior in the class.

The introduction consists of dividing the students of the group into subgroups of 6 people and each participant in the subgroup is assigned a number from 1 to 6 (in one subgroup there should not be tasks with the same numbers). All members of the subgroup are equal participants of the lesson and have equal positions.

Main part. A practical lesson is the defense of tasks that they were given in advance by students of a subgroup. And every student of a subgroup must know the solution not only of his task, but of all the tasks that were given to this group. The teacher evaluates the work of the subgroup as a whole, not of each student individually, and gives time for discussion of individually received solutions of tasks within the subgroup (15 minutes at the beginning of the class). Each member of the subgroup must be ready to defend the solution of any of the subgroup's tasks, so the task of all the other members of the subgroup - in a joint discussion of the proposed solution - is to achieve an exceptionally correct approach in choosing the solution method and, if errors are found, to correct them. Thus, within the subgroup, all the tasks assigned to the defense for this subgroup are discussed.

Note that the learning process in this form allows the student to acquire the following useful skills: the ability to state the method of solving the task, to defend the correctness of the chosen approach, to answer questions posed by other members of the group (while explaining the solution of their tasks); to go deep into the process of solving the newly stated task, to find inaccuracies in the solution (when discussing the solutions of the tasks of the other members of the group).

One of the factors of good performance can be a good trusting relationship, existing between teachers and students, so most students believe. The others rate the teacher-student relationship as purely business. Evaluating the relationship among fellow students, a significant part of students consider the relationships in the group as benevolent, but it cannot be called cohesive (Iakobiuk et al., 2017).

An important feature of this approach is the involvement of all students, without exception, into the learning process, during which not only the acquired skills are consolidated, but also a situation occurs that allows each student to establish a communication process that ensures the best quality of training of the whole subgroup to defend individual assignments.

When the discussion is completed, the teacher randomly selects one student from the first group (for example, toss a dice and calls the number of the fallen face) to perform the task, and calls the number of the task that he will defend (one can also use the cube). Then he chooses a student from the second group, etc..

The task defense process itself also takes place in an active form, as the student shows the solution of any of his tasks, reasonably shows the effectiveness of the chosen method and answers the questions of the teacher on the subject of discussion (here the student's feedback to the teacher arises). At the time of defense of the task at the board by one of the students, all the students of the group outline the solution of this task in their workbooks.

The number of students that can be selected for an answer from each subgroup is determined by the number of students in the group; the number of tasks assigned for defense, the time designated for such defense, the number of subgroups in the group, etc. For example, if you have 4 subgroups and 2 academic hours to conduct a lesson, you can easily check 3-4 tasks, that is, about 12-16 students can be listened to by a teacher.

Conclusions. At the end of the lesson, the teacher evaluates the work of each group, paying students' special attention to the mistakes made and to the positive moments of the lesson.

7) Project-making. The project method is a set of educational and cognitive techniques that allow solving this or that problem as a result of independent actions of students, with obligatory presentation of these results.

This method can be used to perform a typical calculation in mathematical or economic statistics. The independent organization of selective observation, the processing of the results obtained, and the derivation of conclusions are planned. A presentation of the research and its results can be organized.

According to many scientists and in our opinion, the use of interactive teaching methods provides positive motivation for students to study mathematics, contributes to the formation of a sustainable cognitive interest in the subject, improving the quality of knowledge, creates pedagogical conditions for developing the abilities of students.

Lecture with planned errors caused high intellectual and emotional activity of students. Students were interested in finding errors made by the teacher and at the same time could test themselves. All this created a kind of excitement and activated the psychological activity of the listener (Vinogradova, 2014b). The students found all the errors that the teacher planned. To check the acquisition of the material, a test was carried out on a practical lesson already. Students' acquisition of the lecture material held in interactive form was 100% (students who received an "excellent" score - 60%, "good" - 35%, "satisfactory" - 5%. (Vinogradova, 2014).

The organization of the educational process using interactive teaching technologies contributed to a significant increase in the effectiveness of the process of teaching students in math classes, increasing the motivation of students for educational and professional activities, and their own activity.

The results of experimental work have made it possible to establish a significant change in the attitudes of students toward learning. Students often began to ask questions, completeness and quality of homework increased, the number of students using additional sources of information increased, more students had an interest in additional tasks; initiative and independence in learning the material, conducting experiments, performing assignments and the degree of mastering the content of the teaching material have increased.

Iakobiuk L.I., Vinogradova M.V., Malchukova N.N., Kryucheva Y.V. (2017). Students of agrarian university: social profile in mirror of deviations. ESPACIOS, 38 (40), 17.

Kashlev S.S. (2013). Interactive methods of teaching pedagogy. "TetraSistems".

Kharhanova G.S. (1999). Interactive methods of teaching as a means of forming conflict motivation in schoolchildren. Dissertation of the candidate of pedagogical sciences. Kaliningrad.

Makarova E.L. Using interactive forms of learning to improve the effectiveness of the educational process. Available at : http://www.smtueco.ru/en/items/interactive-forms-of-learning

Odegov Yu. G., Volgin N.A. (2004). Organization, forms and methods of conducting classes and independent work: requirements, conditions, mechanisms: Teaching-methodical manual . Moscow: Publishing House of Russian Academy of Economics.

Sidorenko I.N. (2011). Use of interactive techniques in the teaching of social and humanitarian disciplines. Proceedings of BSTU. №8. Educational-methodical work, 8(146), 115-117.

Surmin Yu.P. (2002). Situational analysis or Anatomy of the Case-method. Kiev: Center for Innovation and Development .

Vinogradova M.V. (2014b) Introduction of interactive forms of learning in the learning process in conducting classes in mathematical analysis with students of the Agrarian University. Scientific works Sworld, 13(1), 29-32.

Vinogradova, M.V. (2014). Interactive forms of the organization of the educational process in the teaching of mathematics with students of an agricultural university. Agro-food policy in Russia, 4(28), 74-75.

Zenina N.V. (2012). Use of active teaching methods in the educational process in the formation of economic thinking of future specialists. Bulletin of the Moscow Financial and Law University. Moscow Finance and Law University, Volgograd affiliate, 2, 195-199.

Tsisar, I.Yu., Shalashnikova, V.Yu. (2012). Directions of development and organization of student science in the sphere of state and municipal management. Materials of the Afanasiev Readings, 1(10): 297-301.

1. Candidate of Pedagogical Sciences, Assoc. Prof. FSBEI of Higher Education "Northern Trans-Ural State Agricultural University". Tyumen, Russian Federation. E-mail: Vinmarvlad@yandex.ru

2. Candidate of Pedagogical Sciences, Assoc. Prof. FSBEI of Higher Education "Northern Trans-Ural State Agricultural University". Tyumen, Russian Federation. E-mail: Lyakobuk@yandex.ru

3. Candidate of Pedagogical Sciences, Assoc. Prof. AEPI of HE "Moscow Finance and Law University MFBA", Volgograd affiliate. Volgograd. Russian Federation. E-mail: zenina.76@mail.ru