

Vol. 39 (Nº 28) Año 2018 • Pág. 21
Carmen Cecilia SÁNCHEZ Zuleta 1; Lillyana María GIRALDO Marín 2; Carlos César PIEDRAHITA Escobar 3; Isis BONET; 4 Christian LOCHMÜLLER 5; Marta Silvia TABARES Betancur 6; Alejandro PEÑA 7
Recibido: 20/02/2018 • Aprobado: 30/03/2018
4. Desarrollo del Estudio de Caso
RESUMEN: El crecimiento exponencial de datos médicos ha generado la necesidad de implementar nuevas técnicas de análisis de la información que apoyen la toma de decisiones. El objetivo de este artículo es identificar el valor agregado que aportan los modelos de minería de datos en la toma de decisiones, sobre la información aportada por el análisis exploratorio. Se utilizó un estudio de casos, para dos conjuntos de datos, que buscan determinar la malignidad de una masa detectada en el seno de un paciente, a partir de los atributos registrados de la masa. Los resultados, muestran un comportamiento complementario de las dos técnicas. |
ABSTRACT: The exponential growth of medical data has generated the need to implement new techniques of information analysis that support decision making. The objective of this article is to identify the aggregated value that data mining models have in decision making in the information given by exploratory analysis. It was used a case study methodology for two data sets, that look to determine the malignity of detected masses, in the breasts of patients, through the interpretation of attributes registered from the mases. The results show a complementary behavior of both techniques. |
Las técnicas clásicas de estadística se han constituido a través de los años en una herramienta útil para la toma de decisiones en diferentes áreas del conocimiento, entre ellas el sector de la salud.
Sin embargo, el crecimiento acelerado de las bases de datos, que en cada uno de los diferentes campos del conocimiento, y entre ellas el sector salud, se están gestando como respuesta a la evolución, desarrollo y articulación de la tecnología en su quehacer diario, se ha hecho necesaria la incursión de los modelos de minería de datos como respuesta a la necesidad creada por esta nube de información. Esta articulación ha permitido registrar una mayor cantidad de atributos relacionados con una misma unidad de estudio, así como ampliar la variedad de formatos en los que se registran y almacenan los datos. Este crecimiento exponencial de las bases de datos ha llevado a que las técnicas clásicas de estadística, utilizadas por los expertos e investigadores no logren develar completamente la información subyacente en el conjunto, haciéndose necesaria la incursión de nuevas técnicas de análisis como las citadas inicialmente.
Ante este panorama, es de interés identificar qué tanta información adicional ofrecen los modelos de minería sobre el análisis exploratorio de los datos, además de determinar si cualquier modelo de minería ofrecerá información adicional. Para esto se realizará un estudio de caso, sobre dos conjuntos de datos, cada uno de los cuales busca determinar la malignidad de una masa detectada en el seno del paciente a partir de las características medidas sobre la masa, buscando apoyar la toma de decisiones oportunas y reduciendo procedimiento que pueden resultar costosos e innecesarios tanto para el usuario como para el prestador del servicio, pues la experiencia muestra que el 70% de las biopsias realizadas, a partir de los resultados de una mamografía, son innecesarias.
Este artículo está escrito en el siguiente orden: primero está el marco teórico, los sigue la metodología, posteriormente se tiene el estudio de caso con sus respectivos resultados y finalmente se presentan un conjunto de conclusiones.
Entre los conceptos relevantes para el desarrollo de este trabajo se encuentra el análisis exploratorio de datos (EDA, por sus siglas en inglés). El propósito principal del EDA es resaltar las características relevantes de cada uno de los atributos en el conjunto de datos, usando métodos gráficos, realizando resúmenes estadísticos clásicos, identificando distribuciones en los datos, y estudiando la intensidad de la relación subyacente entre atributos. El análisis exploratorio incluye tres fases principales: el análisis univariado, el análisis bivariado y el análisis multivariado (Vercellis, 2009).
A través de la exploración de los datos, se puede descubrir información significativa para la solución del problema de interés. Esta información se obtiene de las cotas de los datos, medidas descriptivas de estos y de su distribución. La información obtenida puede ofrecer ventajas oportunas en un proyecto de minería de datos, aumentando el conocimiento y entendimiento de los atributos implicados en el problema (Willians, 2011).
Si bien, el EDA es una herramienta esencial en el proceso de identificar el cómo se ven los datos, cuando la tecnología evoluciona y se hace más accesible a las diferentes áreas del conocimiento, genera un incremento masivo de datos, y la identificación de la información inmersa en ellos se convierte en un proceso más complejo en el que la exploración no basta (Ye, 2014).
Se desarrolla entonces un conjunto de modelos, soportados en diferentes áreas del conocimiento, tales como las matemáticas, la estadística, la computación, entre otras, los cuales se complementan con el EDA para develar la información subyacente en estas grandes nubes de datos. Estos modelos sumados con el EDA y diferentes métodos de validación se consolidan para formar una técnica de análisis de datos conocida como Minería de Datos o en inglés Data Mining. Se puede decir entonces que la minería de datos es un proceso utilizado para descubrir información que permanece subyacente en un conjunto de datos históricos (Han, Kamber, & Pei, 2012).
Resumiendo, el termino Minería de Datos hace referencia al proceso total que involucra la recopilación y análisis de los datos, desarrollo de modelos de aprendizaje inductivo y la adopción de decisiones prácticas y acciones basadas en el conocimiento adquirido (Vercellis, 2009).
En esencia los modelos de la minería de datos se pueden clasificar en supervisados y no supervisados. Para el presente desarrollo se utilizará el modelo de árboles de decisión, como modelos supervisado, y del clúster de K- means como técnica no supervisada.

La representación gráfica de un árbol consta de nodos, hojas y ramas. El nodo principal o raíz es el atributo a partir del cual se inicia el proceso de clasificación. Los nodos internos corresponden a cada una de las preguntas acerca del atributo en particular del problema. Cada posible respuesta a los cuestionamientos se representa mediante un nodo hijo. Las ramas que salen de cada uno de estos nodos se encuentran etiquetadas con los posibles valores del atributo. Los nodos finales o nodos hoja corresponden a una decisión, la cual coincide con uno de los niveles de la variable objetivo (Willians, 2011).
Un criterio de división del conjunto de datos en los modelos de árboles de decisión se soporta en medidas de la homogeneidad de los datos. Existen diferentes formas de medir la homogeneidad, las dos más utilizados son la Entropía, y el coeficiente Gini (Ye, 2014).

Además de comprender los modelos de minería que se utilizarán, es necesario tener claridad sobre los principales términos técnicos que se utilizaran.
Mamografía: Una mamografía es un tipo especial de radiografía de las mamas. Puede ser usado para detectar el cáncer de seno en mujeres que no presentan indicios o síntomas de la enfermedad. También puede ser usada si tiene una masa u otro signo de cáncer de seno (MedlinePlus. Trusted health information for you, 2017).
Biopsía: Es un procedimiento que consiste en extraer o extirpar una pequeña porción de tejido del cuerpo, para examinarla luego en el laboratorio y determinar si hay daños o enfermedad. En la mayoría de los casos, una biopsia es la única prueba que puede indicar con seguridad si un área sospechosa tiene cáncer (MedlinePlus. Trusted health information for you, 2017). En esencia, existen tres formas diferentes de extraer una biopsia, por aspiración con aguja fina, por punción con aguja gruesa, o por método quirúrgico (Society, 2017).
Como estrategía metodológica, se propone para el desarrollo de este trabajo, la realización de una adaptación del método de estudio de casos propuesto por el Banco Interamericano de Desarrollo (BID). El BID establece que un estudio de caso sistematiza procesos, sus momentos críticos, actores y contexto con el fin de explorar sus causas, y entender por qué el proceso objeto de estudio se desarrolló como lo hizo. (BID. Sector de Conocimiento y Aprendizaje, 2011). Bajo la filosofía establecida por el BID, y articulando las estapas del estudio a nuestro contexto se definen los siguientes pasos metodológicos: antecedentes, planteamiento y comprensión del problema, descripción de las bases de datos, análisis de la información, y resultados.
Una vez depurados los datos, el análisis de la información se desarrollará en dos etapas, inicialmente se realizará el análisis exploratorio de los datos, y seguidamente se implementarán los modelos de minería “árboles de decisión” y “K-means”, con sus respectivas validaciones, para proceder finalmente con los resultados.
Los modelos de minería de datos han sido utilizados en los últimos años en datos del sector salud como apoyo al proceso de toma de decisiones, tanto para diagnósticos médicos, como para prevenir enfermedades, o para controlarlas, incluso dentro de los procesos de gestión hospitalaria, o con el propósito de buscar diagnósticos personalizados (Yu & Rao, 2012). Algunos trabajos realizados con datos del sector salud son: el de Escobar Ayona, 2014, donde se implementan modelos para la toma de decisiones en el diagnóstico prematuro del cáncer de mama. Barrientos Martínez, Cruz Ramírez, Acosta Mesa, Rabatte Suárez, & Blázquez Morales, 2009, qienes implementan técnicas de árboles de clasificación para caracterizar los patrones de las mujeres que serán diagnosticadas con cáncer de mama. Dávila Hernández & Sánchez Corales, 2012, utilizan árboles de decisión y k-means como apoyo en la toma de decisiones para el diagnóstico de pacientes con hipertensión. Aznielles Quesada, Wong Pérez, & Rosete Suarés, 2008, Implementan de árboles de decisión para responder al problema clínico del diagnóstico de la tuberculosis; además se discute sobre la clasificación y caracterización de otras enfermedades. Solti & Zhai, 2013, comparan los resultados de un modelo de árboles de decisión con el de regresión y el de Naive Bayes en la predicción de supervivencia de pacientes con cáncer de mama. Hayward, Alvarez, Ruiz, Sullivan, & Tseng, 2010, utilizan diferentes técnicas de minería para el diagnóstico del cáncer de páncreas, entre ellas los árboles de decisión y K-means. Mayer et al, 2013, explica el procedimiento seguido por los centros de control y prevención de enfermedades de EEUU para enfrentar pandemia del virus de la gripa H1N1. Lorena & de Carvalho, 2007, comparan las técnicas de árboles de decisión y maquina soporte vectorial predecir la localización celular de proteínas en bacterias y hongos. Podgorelec, Kokol, Stiglic, & Rozman, 2002, muestran aplicaciones de los árboles de decisión en medicina
Una de las principales ventajas que las técnicas de minería de datos le han ofrecido al análisis de datos se centra en develar la información subyacente que se encuentra en dichos conjuntos, y que las técnicas de estadística clásica no logran percibir dada los grandes flujos de información o características de los mismos. Sin embargo, pese a los múltiples trabajos de minería de datos que se han adelantado en problemas de diagnósticos de enfermedades, muchos de los cuales utilizan modelos de árboles de decisión, y k-means como soporte en la toma de decisiones, en ninguno de ellos se establece con claridad qué información adicional a la suministrada por la exploración de datos, se gana con la aplicación de los modelos de minería citados; y más aún, si es necesario aplicar siempre estos modelos.
Surge así la pregunta: ¿qué tanta información, adicional a la suministrada por el análisis exploratorio de datos tradicional, se está develando con el uso de los modelos de minería de datos: árboles de decisión y k-means?, ¿son realmente estos modelos un soporte adecuado en la toma de decisiones en al diagnóstico de cáncer de mama?
Para el desarrollo de este caso, se han utilizado dos bases de datos procedentes de diferentes fuentes. Donde las unidades de estudio son pacientes cuyos resultados del examen de mamografía mostro la presencia de una masa. A continuación de describen cada una de ellas.
Su fuente procede del Dr. WIlliam H. Wolberg; Hospital Universitario de la Universidad de Wisconsin, Madison, Wisconsin-USA (1992-07-05). Consta de 10 atributos medidos en los enteros con 699 unidades de estudio (Lichman, 2013).
Información relacionada
Cuando un patólogo examina una muestra de tejido en el diagnóstico del cáncer de mama, con el método de aspiración con aguja fina, se tienen presente nueve atributos que hablan de la forma, tamaño y malignidad del tumor. En la Tabla 1 se hace una descripción de estos atributos en la base de datos Wisconsin BreastCancerDatabase.
Tabla 1
Atributos: Wisconsin Breast Cancer Data base
Atributo |
Dominio |
1. Sample code number |
Código que identifica a cada paciente |
2. ClumpThickness |
Espesor de la masa. Se mide como un entero entre 1 – 10 |
3. Uniformity of CellSize |
Uniformidad del tamaño de la célula. Se mide como un entero entre 1 – 10 |
4. Uniformity of CellShape |
Uniformidad de la forma de la célula. Se mide como un entero entre 1 – 10 |
5. Marginal Adhesion |
Adhesión marginal. Se mide como un entero entre 1 – 10 |
6. Single EpithelialCellSize |
Tamaño individual de la célula, entero entre 1 – 10 |
7. BareNuclei |
Núcleo, entero entre 1 – 10 |
8. BlandChromatin |
Cromatina Blanda. Se mide como un entero entre 1 – 10 |
9. Normal Nucleoli |
Nucleoli normal. Se mide como un entero entre 1 – 10 |
10. Mitoses |
Mitosis. Se mide como un entero entre 1 – 10 |
11. Class: Malignidad |
2: benigno, 4: maligno |
La fuente de esta base de datos procede del Prof. Dr. Rüdiger Schulz-Wendtland, Instituto de Ginecología y Radiología, Universidad de Erlangen, Nuremberg, Erlangen, Germany (2007-10-29). El donante fue Matthias Elter del Instituto de Circuitos Integrados de Fraunhofer, Departamento de Procesamiento de Imágenes e Ingeniería Médica, Erlangen, Germany. Consta de 6 atributos y un total de 961 unidades de estudio (Lichman, 2013).
Información relacionada
Este conjunto de datos cuenta con un total de cinco atributos relacionados con el tamaño, forma y densidad de la masa detectada por la mamografía, y una variable objetivo dada por “Severity”, la cual establece si el tumor es maligno o no. En la Tabla 2 se presenta una descripción de cada uno de los atributos del conjunto.
Tabla 2
Atributos: MammographicMass Data
Atributo |
Dominio |
1. BI-RADS |
Evaluación: 1 to 5 (ordinal) |
2. Age |
Edad del paciente en años (entero) |
3. Shape |
Forma de la masa, categorizada en: round=1 oval=2 lobular=3 irregular=4 (nominal) |
4. Margin |
Margen de la masa, categorizada en: circumscribed=1 microlobulated=2 obscured=3 ill-defined=4 |
5. Density |
Densidad de la masa, categorizada en: high=1 iso=2 low=3 fat-containing=4 (ordinal) |
6. Severity |
Benigno=0 o maligno=1 (binominal) |
En el proceso de realizar una depuración del ruido que se pueda encontrar inmerso en cada una de las bases de datos, se procedió a detectar los valores faltantes que se encuentran en los conjuntos. Pese a las diferentes técnicas que existen para realizar una imputación apropiada de datos faltantes, y considerando que no se tiene acceso a la fuente original de estos, además de que algunas de las variables requieren de dicha fuente para poder garantizar una imputación confiable, se decidió eliminarlos del conjunto. De esta manera, la base de datos 1 quedó conformada por 683 observaciones, un total de 10 atributos y una variable objetivo; y la base de datos 2 dispone de 815 observaciones, 5 atributos y una variable objetivo.
Datos 1. "Wisconsin Breast Cancer Database"
En la descripción de la base de datos, se indica que la variable objetivo para el conjunto es la variable “Class”, que clasifica cada tumor según dos categorías, “Benigno = 2” o “Maligno = 4”. Teniendo presente esta clasificación, se presenta en la Figura 1 los diagramas de cajas y bigotes por atributo según la malignidad del tumor.
En general, estos gráficos permiten visualizar, que cuando la masa es maligna, la dispersión en todos los atributos es alta, y los valores que asumen las variables son mayores en relación a los correspondientes valores asumidos en el caso benigno. De manera contraria, para el caso benigno se encuentra baja dispersión, pese a la presencia de algunos valores atípicos, y con excepción de las variables “Clum Thickness” y “Bland Chromatin”, se observa que, en general, el valor asumido por las masas, en este caso, es el mínimo valor que pueden asumir los atributos. Más aún, se puede afirmar que el 75% o más de las medidas benignas, se encuentran por debajo del primer cuartil de las medidas de los correspondientes atributos en el caso maligno. Es de resaltar en estos gráficos, que con excepción de la variable “Mitosis”, en los demás atributos el 50% de las masas malignas asumen valores por encima de cuatro.
Complementando lo que develan los gráficos de la Figura 1. Se presenta en la Figura 2., los diagramas de barras para los diferentes atributos, según la malignidad. En estos diagramas se puede visualizar con más detalle el comportamiento de la dispersión explicado en el párrafo anterior, puntajes altos para el caso maligno y bajos para el caso benigno. Note que las variables “Clumtickness” y “Bland.Chromatin” presentan una mayor dispersión para el caso benigno, como se indicó en el párrafo anterior, logrando incluso valores superiores a seis (Ver Figuras 1 y 2). En el caso maligno, es común ver que los valores que asumen las masas se concentran en el último valor (10), o en valores altos, con excepción de la variable “Mitosis”, pese a esto, para este caso, la dispersión es mayor, con tendencias más asimétricas que el caso benigno, con marcadas colas a izquierda como se observa en la Figura 3.
Figura 1.
Distribución de los atributos de la base BreastCancer

------
Figura 2
Diagramas de barras de los atributos según la Malignidad

En la Figura 3., se presenta el ajuste de la distribución para cada uno de los atributos según la malignidad del tumor, con un tono rosa para el caso benigno, y azul para el maligno. Se observa en el gráfico la alta dispersión del caso maligno, y la concentración en valores bajos para el caso benigno. En general, para el caso benigno, las curvas presentan comportamientos casi simétricos, con excepción de la variable “Bland.Chromatin”, con pequeñas colas marcadas por los puntos atípicos que se mencionaron anteriormente. No sucede lo mismo con el caso maligno, donde las curvas se extienden por todo el dominio y en la mayoría de ellas no presentan una concentración especial en algún valor, además no se observa comportamiento simétrico en ninguno de los atributos para este caso.
Figura 3
Ajuste de Atributos según la Malignidad del Tumor
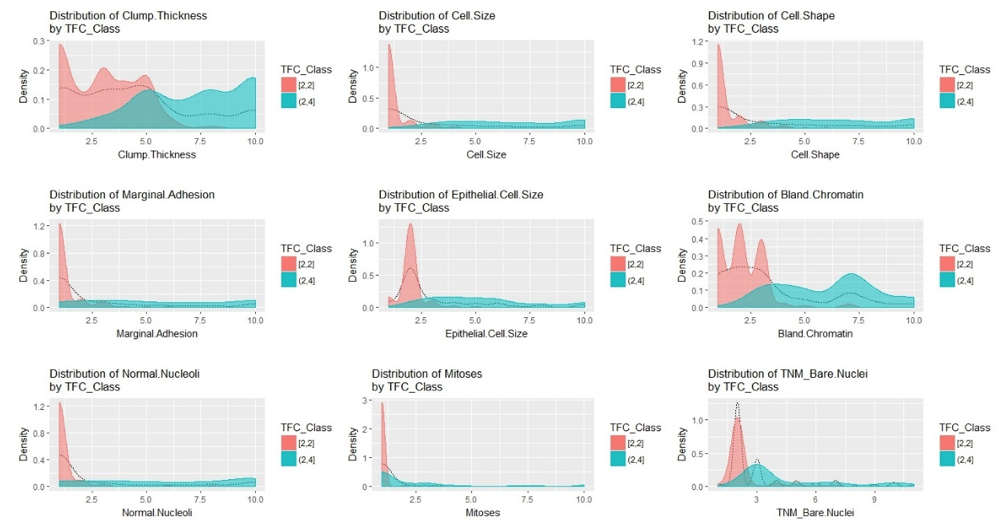
Se observa en la Figura 3, que la curva de distribución ajustada de las variables “Cell.Size”, “Cell.Shape” y “Marginal.Adhesion” presentan un comportamiento similar, tanto en el caso benigno como maligno. Se realiza entonces un análisis de correlación entre las variables en general el cual mostró una relación de dependencia positiva. Sin embargo, solo las variables tamaño y forma de la célula (“Cell.Size”, “Cell-Shape”) presentan una relación lineal estrecha, en cada caso de malignidad (ver Figura 3).
La variable objetivo para este conjunto de datos es “Severity”, cuenta con dos niveles, benigno denotado por “0” y maligno denotado con “1”. El conjunto de datos tiene una variable numérica “Edad”, y las demás ordinales.
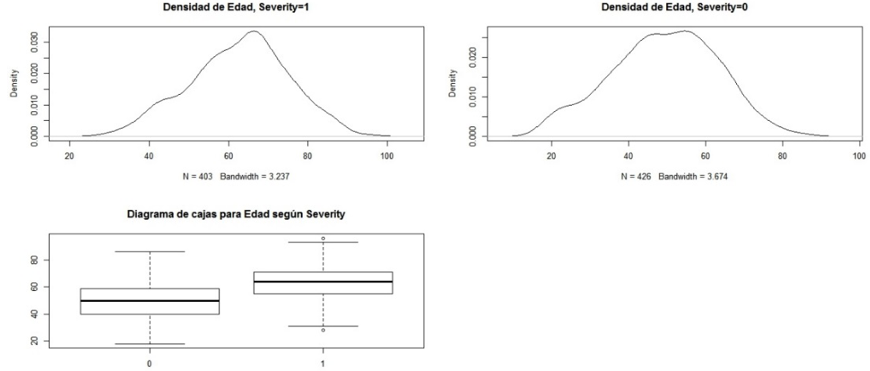
En la Figura 4 se presenta un resumen sobre dispersión y distribución de la variable “Edad”, en relación a la malignidad de la masa. En el diagrama de cajas y bigotes (gráfico inferior de la figura) se observa que la dispersión de la edad es similar en los dos casos. Con una edad promedio de 49 años para el caso benigno y de 62 en el maligno, se confirma el desplazamiento a derecha de la medida de tendencia central de la edad en cada uno de los casos. De hecho, mediante una prueba de Wilcoxon Rank, a una significancia del 5%, se evidencia la anterior afirmación, al rechazar la hipótesis nula, y concluir que efectivamente las medianas de la edad, en estos grupos, no son iguales, lo que permite confirmar que efectivamente la edad de los pacientes cuyas mamografías muestran masas que resultan malignas es mayor que la de aquellos cuyos resultados fueron benignos. Las curvas de ajuste de la distribución de la variable edad, permiten observar el desplazamiento citado. En esta se observa que tanto el caso maligno como el benigno tienen una distribución similar y relativamente simétrica, solo que se encuentra un desplazamiento a derecha de la curva para el caso de malignidad (Ver Figura 4. Parte superior).
Figura 4
Ajuste y diagrama de cajas para la
edad según la malignidad del tumor
-----
Figura 5
Diagrama de barras para los Atributos de “MammographicMass
Data” según la Malignidad de la masa

En la Figura 5 se presenta el diagrama de barras para el resto de atributos según la variable “Severity”. En términos generales, se puede observar que entre mayor es el nivel de clasificación de la variable, mayor probabilidad hay de que el resultado sea maligno, con excepción de la variable “Density”, en la que las unidades de estudio se centran en el nivel tres sin importar la malignidad de la masa, implicando que, por sí sola, esta variable no tiene incidencia directa sobre la malignidad de la masa detectada. Note además que la variable “BI-RADS” logra mostrar una discriminación un poco más marcada que los demás atributos, al lograr clasificar un porcentaje elevado de los casos benignos en el nivel cuatro o menos, y una concentración elevada de los casos malignos en el nivel cinco. Observe en esta figura, que tanto para el caso maligno como benigno la dispersión es alta en la mayoría de los atributos, y que si bien hay algunas tendencias que se observan en ellos, según de los niveles de la variable objetivo, estos no son determinantes en la malignidad de la masa.
Para realizar la implementación de los modelos árboles de decisión y k-means, se ha hecho uso de la herramienta R, y de su librería “rattle”. Es importante anotar que esta es la misma herramienta que se utilizó para realizar la exploración de los datos expuesta anteriormente. A continuación, se presentan los resultados y análisis para los modelos de minería: árboles de decisión y k-means para cada una de las bases de datos en estudio.
Modelo: árboles de decisión. Base de datos 1. "Wisconsin Breast Cancer Database"
La tabla de la izquierda en la Figura 6, muestra que la complejidad más apropiada para la construcción del árbol en este conjunto de datos es de 0.010, el cual proporciona un error de 0.121121 y una profundidad de cuatro en el árbol.
A la derecha de la misma figura se muestra el árbol que se obtiene para los datos en estudio con los parámetros establecidos. Este modelo presenta sólo dos variables como incidentes en la malignidad de la masa. Si el valor del tamaño de la célula, “Cell.Size”, es menor que 2.5 se podría decir que el tumor es benigno, note que el 62% de las masas en el conjunto de entrenamiento fueron clasificadas bajo esta regla, con un error del 3%; y si valor de la variable es superior a 4.5, se tendría que efectivamente la masa es maligna, el 25% de las masas con un error del 1%, resultados independiente de las otras variables. Si el valor de esta variable se encuentra entre 2.5 y 4.5, lo que sucede en el 14% de las masas restantes, el resultado dependerá de una nueva variable, “Bare.Nuclei”. En este caso, valores superiores a 3.5 indican malignidad en el tumor, es decir niveles de 4 a 10, con un error del 14%, y lo contrario para los niveles de 1 a 3, con un error del 28%.
Figura 6
Complejidad (izq.) y Árbol (Der.) para datos 1.
"Wisconsin Breast Cancer Database"

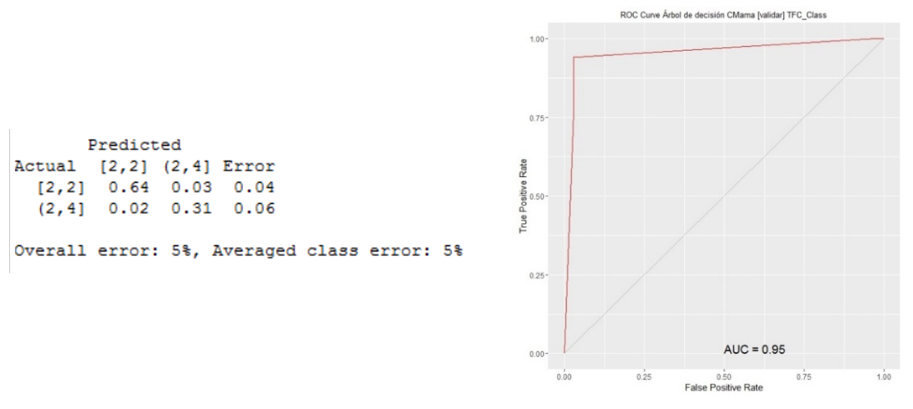
Para estudiar la validez del modelo se construyeron la matriz de confusión y la curva ROC (ver Figura 7). En ambos casos se observa un error total de clasificación del 5%. La curva ROC muestra por su parte un área de 0.95. La matriz de confusión, además del error total (5%), muestra un error promedio por clase del 5%, encontrándose un error sutilmente mayor para el caso de malignos clasificados como benignos (verdaderos negativos).
Figura 7
Matriz de confusión y Curva ROC para el árbol de la
base de datos 1. "Wisconsin Breast Cancer Database"
Modelo: de k-means. Base de datos 1. "Wisconsin Breast Cancer Database"
Puesto que el modelo de k-means es un método no supervisado, y dado que la variable objetivo en el conjunto de datos cuenta con dos niveles, se ha decidido implementar el modelo de k-means considerando tres clústeres con los que se espera distinguir las masas que resultaron malignas, las benignas, y en un tercer grupo aquellas masas cuyos valores de atributos no las caracterizan de manera determinante en ninguno de los grupos anteriores.
Figura 8
Coordenadas Discriminantes para para el modelo de k-means.
Datos 1. "Wisconsin Breast Cancer Database"
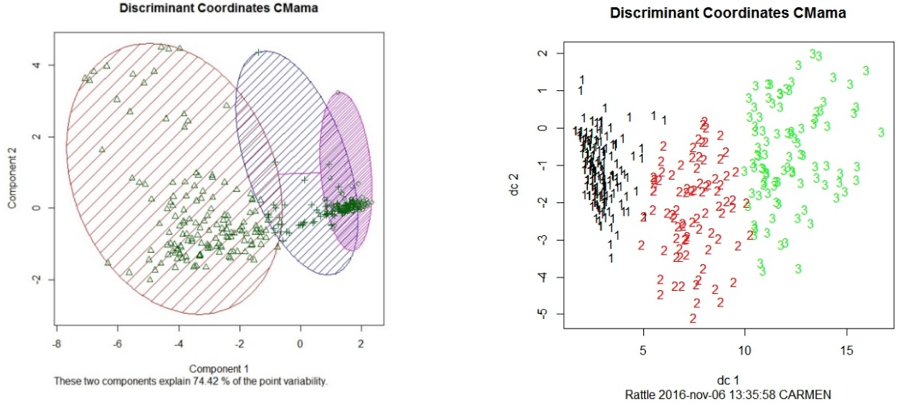
En la Figura 8 se puede observar el comportamiento de los tres clúster de acuerdo a una descomposición en el plano. En el gráfico de la derecha se ve que el primer discriminante es el que realmente está incidiendo sobre la determinación de los clúster. Se puede observar que sólo para el clúster dos, los valores prácticamente negativos del segundo discriminante tienen incidencia, sin ser determinantes para caracterizarlo. Note que los valores del primer discriminante por debajo de cinco prácticamente caracterizan el clúster uno, los superiores a 10, caracterizan el clúster tres, y se puede notar como el clúster dos, se mueve entre valores del primero que van de 5 a 10, aproximadamente. De manera análoga, en el gráfico de la izquierda se observan dos clústeres claramente distinguidos por las componentes y uno que se logra traslapar, con una variabilidad explicada por las nuevas componentes del 74.42%.
Si bien los gráficos de la Figura 8 permiten observar tres clúster claramente definidos y discriminados, no necesariamente implica que se está realizando una clasificación de acuerdo a la necesidad del problema, es decir, dado que el análisis de clúster es una técnica no supervisada, se debe evaluar la precisión que se tiene con el modelo al clasificar los pacientes de acuerdo a la malignidad de la masa y no en relación a otras características de homogeneidad que puedan existir.
Tabla 3
Resultado Clúster Cáncer de Mama

El resultado de la clasificación de los clusteres, así como la influencia de cada uno de los atributos en cada clúster se puede observar en la tabla 3. Note que un porcentaje muy elevado de las unidades de estudio fueron asignadas al primer clúster (310), en tanto que el segundo y tercero cuentan con una tercera parte de elementos del primero. Para evaluar la contribución de cada atributo en los diferentes clústeres se analizan sus promedios. En general, los centros de los grupos muestran todas las variables tienen una contribución en cada uno de los clústeres, lo que evidencia que no hay contribución especial de alguna de las variables en algún clúster, lo que permite intuir que el modelo no parece estar aportando al propósito de clasificar las masas según la malignidad. Una revisión de la asignación de masas en los clústeres mostró que efectivamente no se está realizando una clasificación según la malignidad.
En el gráfico de la izquierda de la Figura 9, se observa que a una complejidad de 0.012 se logra el menor error que es de 0.5, lo que define un árbol de profundidad cinco.
En el diagrama de árbol, se observa como primer atributo en la partición a “Bi-Rads” tal que si asumen una categoría superior a cuatro (con una precisión del 91%) indica que la masa será maligna, en caso contrario, la malignidad dependerá de la variable forma (“Shape”), si esta asume las categorías 1, 2 o 3, entonces se puede establecer que la masa no es maligna (con una precisión del 89%), pero si está en la cuarta categoría, la malignidad dependerá de la edad del paciente, de tal manera que si el paciente tiene una edad de 69 años o más la masa será maligna (con una precisión del 87%), y si la edad es menor o igual a 69 años la malignidad dependerá de la variable margen (“Margin”), de tal manera que si la masa asume en esta variable un valor superior a tres se entiende que la masa será maligna (55% muy débil en este caso) y en los casos restantes no habrá malignidad.
Figura 9
Complejidad (izq.) y Árbol (Der.) para Cáncer Mama

-----
Figura 10
Curva ROC para la Masa Mamográfica

En la Figura 10. se presenta la curva ROC para evaluar el desempeño del modelo del árbol, en este caso se tiene un área bajo la curva del 0.88, lo que indica una buena relación entre los casos positivos identificados de manera correcta por el modelo (verdaderos positivos), contra aquellos que fueron clasificados de manera errónea. También se analizó la matriz de confusión para un conjunto de validación, en este caso, se logró un error promedio del 17%, y un error por clase del 18%, por lo que se tiene una clasificación acertada promedio del 83%. Se concluye que el modelo presenta resultados satisfactorios en la detección de la malignidad de la masa detectada por la mamografía.
Modelo: K-means. Base de datos 2. " Mammographic Mass Data "
De manera análoga al conjunto anterior, se construyeron tres clústeres con el mismo propósito de clasificación.
En el gráfico de la derecha de la Figura 11. se muestran los tres clústeres claramente discriminados. Para los clústeres 2 y 3 se observa cierta relación de dependencia lineal, creciente y decreciente respectivamente, entre las coordenadas discriminantes. El primer clúster sin embargo no presenta ningún comportamiento especial entre las coordenadas. El gráfico de la izquierda de la misma figura muestra algunos elementos claramente distinguibles, sin embargo, existe una gran cantidad de puntos concentrados en los que no se logra determinar cómo inciden los compontes en los clústeres.
Figura 11
Coordenadas Discriminantes para
Masa detectada por Mamografía

En la Tabla 4 se observa que la mayor concentración de masas se encuentra en los clústeres dos y tres, por lo que se esperaría que estos sean los que clasifican las masas según su malignidad, en tanto, que, por la concentración, se esperaría que en el clúster uno se encuentren las masas cuyos atributos no permiten clasificarlas de manera determinante según su malignidad. Para verificar si efectivamente es esto lo que está sucediendo, se analizará una validación.
La evaluación de los centroides, en la Tabla 4, muestra que la participación, respecto a la media de la variable densidad “Density”, es prácticamente igual para los tres clusters, y por su proximidad al promedio, se tiene que no hay incidencia significativa de la variable en ninguno de los grupos. Para el primer clúster, se podría decir que en relación a las respectivas medias, las variables Forma (“Shape”) y Margen (“Margin”) resultan parcialmente incidentes, con una participación de -0.3261643 de la primera, y 0.510041 de la segunda. En cada uno del segundo y tercer clúster se observan las mismas variables como incidentes, con una participación baja de las variables restantes.
Tabla 4
Clúster Masas de Mamografías
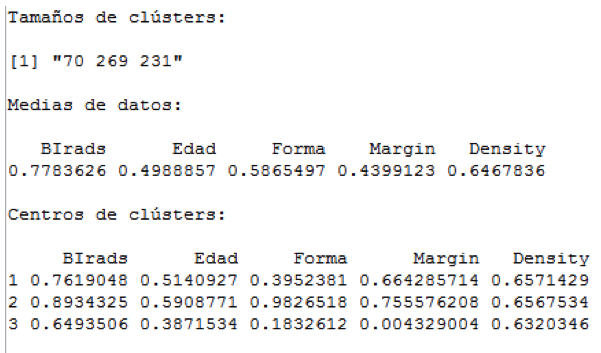
Estos resultados muestran que si bien se logran determinar tres clústeres con la característica de homogeneidad intra grupos, y heterogeneidad entre grupos, estos no están clasificando de acuerdo a la variable respuesta, como se deseaba. Para confirmarlo se evalúa el modelo, obteniéndose una clasificación de todos los elementos en el clúster dos, sin importar el nivel de la variable respuesta al que pertenezcan. Una vez más, la técnica de k-means genera clústeres discriminados pero no en términos de la malignidad de la masa estudiada, por lo que no ofrece resultados satisfactorios.
En cada uno de los dos casos en estudio, el análisis exploratorio de los datos ha suministrado información relevante sobre el comportamiento de los respectivos atributos en relación a la malignidad de la masa. Ha permitido estudiar su distribución, dispersión y concentración, así como la relación de dependencia entre ellos. En ambos casos, a partir de estos análisis se puede formar una idea de la tendencia de los atributos cuando la masa es maligna, permitiendo lanzar algunas conjeturas a partir de los resultados obtenidos, como sucede cuando se afirma que “entre mayor es el valor que asume el atributo, mayor es la probabilidad de que la masa sea maligna”, conjetura a la que se llega en ambos casos, y que se observa tanto en las curvas de distribución como en los diagramas de barras y gráficos de cajas y bigotes.
Pero una conjetura no suministra suficiente evidencia que pueda soportar la toma de decisiones, y en ninguno de los dos casos, se logra identificar, específicamente a partir de qué valor del atributo, se puede hablar de la malignidad de la masa. Mas aún, el análisis exploratorio no muestra si la malignidad obedece a un cruce de patrones entre dos o más atributos, aunque se realizara una exploración múltiple en los datos.
Ahora bien, en ambos casos, la implementación de los modelos de minería ha presentado resultados satisfactorios para el caso de árboles de decisión, más no sucede lo mismo con el modelo de K-means, el cual logra formar los clústeres bien discriminados, más no entorno a la variable objetivo. Así entonces, para los casos en estudio, se puede decir que este modelo no suministra información adicional relevante a la encontrada en el análisis exploratorio.
Los árboles de decisión ofrecieron, en ambos casos, resultados más confiables en la solución del problema y soporte en la toma de decisiones. Pues este modelo, ha permitido identificar los atributos que son efectivamente incidentes en la malignidad de la masa, además de develar a partir de qué valor del atributo se puede observar la malignidad de esta, y más aún, permite determinar cuántos atributos y a partir de qué valores, intervienen para diagnosticar malignidad de la masa.
Se tienen entonces que este modelo ofrece, a la solución del problema de la detección de la malignidad de la masa, una buena cantidad de información adicional a suministrada por el análisis exploratorio. Con los procesos de validación, se cuenta con cierto grado de confiabilidad al momento de tomar decisiones a partir de sus resultados, lo que no se logra con la simple exploración. Sin embargo, es evidente que la implementación de modelos sin exploración de datos no sería una metodología recomendable para un estudio que involucre tratamiento de datos.
En general se puede concluir que, si bien el análisis exploratorio no constituye un análisis lo suficientemente fuerte como para soportar de manera definitiva la toma de decisiones, sí se puede decir que es relevante en cualquier estudio de datos, puesto que es este análisis quien entrega el primer acercamiento al comportamiento de los atributos y variables objetivos.
Note que no siempre un modelo de minería puede entregar información adicional a la encontrada en el análisis exploratorio. En este caso se ha encontrado, en cada una de las bases de datos, que el modelo de k-means realiza una buena clasificación del conjunto de datos, pero no lo hace en relación a la variable objetivo, por lo que la información adicional suministrada por el modelo no apunta a mejora la toma de decisiones entorno a la malignidad de la masa.
Pero no sucede igual con el modelo de árboles de decisión. Para estos modelos se encontró unos resultados satisfactorios en los dos conjuntos estudiados, con valores ROC del 95% para el caso de Cáncer de Mama y del 88% para los datos de las Masa detectadas por la Mamografías, los que validan al modelo como aptos para apoyar la toma de decisiones de la malignidad a partir de los atributos de las masas detectadas. Como se decía en los resultados, este modelo aporta información trascendental al problema, más allá de los resultados encontrados en el análisis exploratorio.
Es importante anotar que la poca cantidad de unidades de estudio se puede ver refleja en modelo poco eficientes o no muy confiables, y que los resultados obtenidos en el modelo de k-means podrían mejorar si se dispusiera de mayor cantidad de información. Pues conjuntos de datos formados por pocas variables, o más aún, con una cantidad pequeña de unidades de estudio, puede llevar a encontrar modelos no muy confiables, o incluso puede ocurrir que el modelo no se pueda implementar.
En general, con base en el estudio que se presenta en este material, se recomienda, sobre los dos modelos implementados, la aplicación del modelo de árboles de decisión en la caracterización de la malignidad de una masa de seno.
Quesada, A. , Wong, Y., Pérez, D., y Rosete Suarés, A. (diciembre, 2008). Minería de Datos aplicada a la Gestión Hospitalaria. 14 Convención Científica de Ingeniería y Arquitectura. 2-5. Cujae, Cuba.
Barrientos, R., Cruz, N., Acosta, H. G., Rabatte, I. G., y Blázquez, S. L. (2009). Árboles de decisión como herramienta en el diagnóstico médico. Revista Medica de la Universidad de Veracruz, 9(2), 19-24.
BID. (2011). Banco Interamericano de desarrollo (BID). Recuperado de: https://publications.iadb.org/bitstream/handle/11319/6434/Pautas%20para%20la%20elaboraci%C3%B3n%20de%20Estudios%20de%20Caso.pdf
Chandola, V., Sukumar R., S., y Schryver, J. (2013). Knowledge Discovery from Massive Healthcare Claims. En KDD2013, 1312-1320.
Dávila, F., y Sánchez , Y. (2012). Técnicas de minería de datos aplicadas al diagnóstico de entidades clínicas. Revista Cubana de Informática Médica, 4 (2), 174-183.
Escobar Ayona, E. M. (2014). Tecnología Big Data para el Sector Salud del Estado de Guerrero. Research in Computing Science, 77, 167-174 .
Han, J., Kamber, M., y Pei, J. (2012). Data Mining Concepts and Techniques. New York: Elsevier.
Hayward, J., Alvarez, S. A., Ruiz, C., Sullivan, M., y Tseng, J. (2010). Machine learning of clinical performance in a pancreatic cancer database. Artificial Intelligence in Medicine, 49, 187-195.
Lichman, M. (2013). UCI. Machine Learning Repository. University of California, School of Information and Computer Science. Recuperado de https://archive.ics.uci.edu/ml/datasets/Breast+Cancer+Wisconsin+%28Original%29
MedlinePlus (09 de 2017). Trusted health information for you. Recuperado de https://medlineplus.gov/mammography.html
Podgorelec, V., Kokol, P., Stiglic, B., y Rozman, I. (2002). Decision trees: an overview and their use in medicine. Journal of Medical Systems, 26(5), 445-463.
Sanders, G. (2009). Introduction to Medical Decision Making and Decision Analysis. Durham, NC: Duke Clinical Research Institute.
Society, A. C. (5 de 02 de 2017). American Cancer Society. Recuperado de https://www.cancer.org/es/cancer/cancer-de-seno/pruebas-de-deteccion-y-deteccion-temprana-del-cancer-de-seno/biopsia-del-seno.html
Solti, D., y Zhai, H. (2013). Predicting Breast Cancer Patient Survival Using Machine Learning. Proceedings of ACM - BCM, 704-705. Washington, DC, USA.
Sox.H.C., Blatt,M.A., M.C., H., & Marton, K. (1988). Medical Decision Making. Bostom, MA: Butterworth-Heinemann Publisher.
The Free Dictionary by Farlex. (23 de 02 de 2017). Obtenido de Medical Diccionary. Recuperado http://medical-dictionary.thefreedictionary.com/fractional+shortening
Vercellis, C. (2009). Business Intelligence: Data Mining and Optimization for Decisition Making. United Kingdom: Wiley .
Willians, G. (2011). Data Mining with Rattle and R: The Art of Excavating Data for Knowledge Discovery. Londres: Springer.
Ye, N. (2014). Data MIning. Theories, Algorithms, and Examples. New York: CRC press.
1. Ms. En Matemáticas & Ms. En Estadística Aplicada. Facultad de Ciencias Básicas. Universidad de Medellín. (participa en el pregrado y maestría en Modelación y Ciencias Computacionales). - Colombia. Universidad de Medellín. ccsanchez@udem.edu.co
2. Doctor en Tecnologías de la Información y Comunicación. Facultad de Ingenierías. Universidad de Medellín. Ingeniero en Ingeniería de Sistemas (Profesor de los programas de pregrado y posgrado en gestión de la información y de conocimiento y profesor de doctorado en Administración de la facultad de administración). lmgiraldo@udem.edu.co
3. PhD. Matemática Aplicada. Facultad de Ciencias Básicas. Universidad de Medellín. (participo en el pregrado y maestría en Modelación y Ciencias Computacionales). cpiedrahita@udem.edu.co
4. Doctora en Ciencias Técnicas. Departamento de Sistemas. Universidad EIA, Envigado, Colombia. Ingeniera en el Programa de Ingeniería de Sistemas y Computación. ibonetc@gmail.com
5. MSc en Sistemas. Departamento de Economía y Finanzas. Universidad EIA, Envigado, Colombia. Administrador de Empresas en el Programa de Ingeniería Financiera. chris.lochmueller@gmail.com
6. Doctora en Ingeniería. Departamento de Sistemas e Informática. Universidad EAFIT, Envigado, Colombia. (Profesora de los programas de pregrado y posgrado en ingeniería de sistemas). mtabares@eafit.edu.co
7. Doctor en Ingeniería. Departamento de Sistemas. Universidad EIA, Envigado, Colombia. Ingeniero en el Programa de Ingeniería de Sistemas y Computación. pfjapena@gmail.com