ISSN 0798 1015

Vol. 39 (Nº 24) Año 2018 • Pág. 32

Metodología basada en simulación para la programación de recursos en líneas de confección

Resource planning methodology based on simulation in clothing production lines

CANO, Jose A. 1; CAMPO, Emiro A. 2; GÓMEZ-MONTOYA, Rodrigo A. 3

Recibido: 24/01/2018 • Aprobado: 22/02/2018

Contenido

1. Introducción

1. Introducción

Las tendencias de consumo globales en la industria de la confección y moda exigen que las empresas que se desempeñan en este sector ofrezcan una amplia variedad de productos, lo cual implica que se pase de un concepto de fabricación en masa a un concepto de fabricación personalizada, con tamaños de lote pequeños, que a su vez implican un alto número de alistamientos y preparaciones para la producción. Esta situación ha causado que las cadenas de suministro se enfoquen en minimizar los tiempos de producción, aumentando así la capacidad de respuesta a las cambiantes demandas del mercado, brindando productos de alta calidad a un costo adecuado (Cano, Campo, & Gómez, 2018; Rojas, Guisao, & Cano, 2011).

La intensa competencia en mercados nacionales e internacionales genera inestabilidad en la industria de confección y textiles, sin embargo, esta industria podría volver a posicionarse como una industria vigorosa con una capacidad de desafiar a los competidores tanto a nivel nacional e internacional. Esto puede lograrse a través de la innovación tecnológica y estrategias de manufactura efectiva tales como la personalización masiva, que bajo un escenario competitivo exigen superar las limitantes que hasta ahora han impedido la automatización en la confección de prendas de vestir (Bonsignorio & Molfino, 2006; Ramdass & Pretorius, 2011). Igualmente, aspectos como el capital humano, desarrollo tecnológico, infraestructura empresarial, innovación y conocimiento, tamaño de mercado, entre otros, influyen en la competitividad de un sector empresarial (Cano, Panizo, García, & Rodríguez, 2015a), y permiten generar cadenas de suministro que en cada sistema logístico se alinean con la productividad y competitividad empresarial, satisfaciendo así los requerimientos de los clientes (Cano, Panizo, García, & Rodríguez, 2015b).

Dentro de estos sistemas logísticos, se encuentra la logística interna, que se encarga de los procesos productivos, transformación, agregación de valor y prestación de servicios (Rojas, Guisao, & Cano, 2011), y que en el caso de la industria de la confección y moda estos procesos productivos pueden desarrollarse a través de una amplia variedad de sistemas de producción, tales como los que se muestran en la Tabla 1. Estos sistemas de producción buscan reducir el tiempo de procesamiento de una prenda de vestir o un lote (suma total de tiempo de trabajo de todas las operaciones de fabricación), el tiempo de transporte entre departamentos,  operaciones o máquinas para las prendas en proceso o terminadas, el tiempo de almacenamiento temporal o de espera de las prendas para el inicio de la próxima operación, y el tiempo de inspección para detectar cualquier defecto durante la fabricación o en las prendas terminadas antes de su empaque (Rameshbabu, 2006).

Tabla 1
Sistemas de producción para la confección de prendas de vestir

Fuente: Elaboración propia

Con el fin de alinear los procesos productivos con los demás procesos logísticos y empresariales, tales como el abastecimiento y gestión de proveedores (Gómez, Cano, & Campo, 2016), sistemas de planificación de la producción (Arango, Cano, & Alvarez, 2012), almacenamiento y despacho eficiente de productos (Cano, Gomez, & Salazar, 2017) (Salazar, Gomez, & Cano, 2017), distribución y transporte (Andrejić, Bojović, & Kilibarda, 2016), los procesos de fabricación y manufactura en el sector de la confección han dejado de ser sistemas tradicionales de fabricación en línea para transformarse en sistemas de producción modular, que facilitan la aplicación de sistemas de respuesta rápida, tales como los sistemas Pull y justo a tiempo (Ko, 2001; Sarache, Cespón, Ibarra, & Alonso, 2004).

Como tal, un sistema modular en la industria de la confección y moda procesa pequeños tamaños de lote, en una configuración donde por lo general el número de operarios es inferior al número de máquinas o puestos de trabajo; por lo cual, se reducen los inventarios en proceso, se aumenta la tasa de producción y se balancea la carga asignada a los operarios (Abend, 1999; Buzacott, 2004). De esta forma, el balanceo del sistema se logra por la habilidad de los operarios de moverse dentro del módulo, buscando una utilización de operarios cercana al 100%, mientras que la utilización de estaciones de trabajo varía ampliamente como función de los tiempos de ciclo de cada estación (Wang, Schroer, & Ziemke, 1991). Sin embargo, un sistema de producción modular está sujeto a una amplia gama de variables y parámetros que por su naturaleza con estocásticos y dinámicos, tal y como lo son el tamaño de los lotes a procesar, el número de lotes que se liberan a producción, el personal disponible en los módulos, personal disponible para realizar alistamientos y preparaciones de referencias, tiempos de alistamiento y preparación, que hacen que el problema de optimización de la producción en ambientes de confección no sean viables en tiempo polinomial (Allahverdi, Ng, Cheng, & Kovalyov, 2008).

Por lo tanto, para enfrentar este tipo de problemas, la simulación discreta permite representar procesos y crear escenarios que faciliten el entendimiento, aprendizaje, y la toma de decisiones en procesos de planeación, ejecución y control de procesos logísticos y operativos (Cano, Campo, & Gómez-Montoya, 2017; Gómez, Zuluaga, & Cano, 2014). En este sentido, por medio de la simulación de sistemas que se puede analizar los costos de demoras, costos de tiempos perdidos, costos de contratación de mano de obra, costos de inversiones en infraestructura bajo diferentes escenarios, variando la cantidad y rendimiento de los recursos y espacios actuales (Hillier & Lieberman, 2010).

Para el caso de la industria de la confección, se ha evidenciado la utilidad que brinda la simulación para la planificación de la producción en sistemas de producción modular, en este sentido, autores como McNally y Heavey (2004) realizan una investigación en una empresa mediana que fabrica una amplia variedad de productos por lotes, y desarrollan un software de simulación para la planificación estratégica y de corto plazo, encontrando problemas en el mantenimiento del modelo y recolección de datos. Igualmente, autores como Cano, Campo y Gómez (2018) solucionan el problema de planificación de producción con variables estocásticas en una planta de confección modular a gran escala, utilizando un modelo de programación mixta que se alimenta los resultados de un modelo de simulación de eventos discretos.

Como consecuencia, este artículo tiene como objetivo desarrollar un modelo de simulación discreta que permita evaluar diferentes escenarios para la toma de decisiones en un sistema de confección modular, con el fin de determinar el tiempo perdido en módulos de confección y equipos de montaje. Para esto, se presenta en la Sección 2 se presentan las especificaciones del modelo de simulación para el sistema de confección modular, así como el código de programación para la simulación en Visual Basic Applications para MSExcel, de tal forma que la adaptación y mantenimiento del modelo de simulación, así como el ingreso de información de las variables sea de fácil manejo para los usuarios. En la Sección 3 se presentan los resultados obtenidos con el modelo de simulación para los escenarios planteados, y finalmente en la Sección 4 se presentan las principales conclusiones de este estudio.

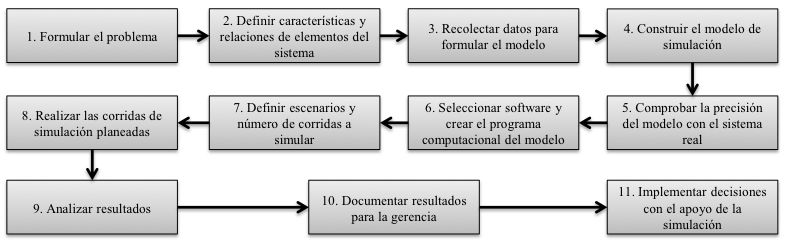
Para garantizar la idoneidad de un modelo de simulación y los resultados obtenidos, es necesario aplicar un proceso secuencial que permita ir desde la formulación del problema hasta la toma de decisiones que se realiza con base a los resultados arrojados por la simulación. El conjunto de etapas desarrolladas en este estudio se muestran en la Figura 1.

Figura 1
Metodología para la creación del modelo de simulación

En la empresa en estudio, existe una estrategia de planificación y programación de las plantas de confección desarrollada para abastecer un mercado que demanda prendas de vestir básicas, donde el número de referencias de prendas por pedido son pocas y en grandes cantidades por prendas, lo cual permite que se programen grandes lotes de producción, incurriendo en pocos montajes y alistamientos en las plantas de confección. Sin embargo, en la actualidad el comportamiento del mercado exige prendas de vestir que se adapten a una personalización de los diseños, conllevando a que la empresa lance más colecciones por año, mayor número de referencias por colección y menor número de unidades por referencia. El tiempo de almacenamiento de prendas se pretende reducir a cero mediante la combinación sincronizada de almacenamiento y transporte entre puestos de trabajo de los módulos de confección, es decir, que los productos en proceso se encuentren el menor tiempo posible estáticos, y por lo contrario se encuentren en movimiento o transformación.

El sistema de producción modular, se compone principalmente por canaletas, módulos de confección y equipos de montajes. Las canaletas son los espacios físicos donde se instalan los puestos de trabajo para procesar una referencia de una prenda de vestir, y se componen de las máquinas y puestos necesarios para esto. Los módulos de confección son equipos de personas (operarios) que se encargan de operar las máquinas de los puestos de trabajo para realizar el ensamble de las piezas que componen una prenda de vestir, desempeñando así el proceso de confección. Los equipos de montaje se componen del personal encargado de realizar la preparación y alistamiento de las canaletas para habilitar el procesamiento de una referencia que se encuentre dentro de la programación de producción liberada a la planta de confección. Adicional a esto, la planta de confección trabaja por lotes, que se componen de una única referencia que tiene asignado un determinado número determinado de prendas o unidades a procesar; y el tamaño de lote se especifica por el tiempo estimado (minutos de confección) que se requiere para su procesamiento.

Para la planta de confección de este estudio, en la cual se realizarán las simulaciones sobre diversos escenarios, se ha determinado por estudios previos de balance de línea que un módulo de confección estándar se compone de 10 operarios, mientras que un equipo de montajes se compone por 5 personas (con los tiempos de alistamiento actual). La planta de confección cuenta con una capacidad para albergar 33 canaletas, y 19 módulos de confección para soportar los requerimientos del mercado. De esta forma, en los equipos de montaje pueden alistar referencias mientras que los módulos de confección procesan otra referencia, y una vez un módulo de confección termina de procesar un lote asignado, este se desplaza a la canaleta donde previamente el equipo de montajes realizó la preparación y alistamiento. En caso tal en que un módulo de confección termine de procesar un lote asignado, y no se encuentre una canaleta con el alistamiento y preparación terminada, se generará un tiempo perdido (ocioso) por parte del módulo de confección. En caso tal en que no se cuente con canaletas disponibles para hacer la preparación y alistamiento de una referencia programada, se generará un tiempo perdido (ocioso) por parte de los equipos de alistamiento y montaje.

Por lo tanto, la gerencia de operaciones de la empresa en estudio desea analizar diferentes escenarios, los cuales se componen por el número de equipos de montaje a utilizar, el tiempo estimado para realizar una preparación y alistamiento, y el tamaño de lote expresado en minutos de producción. Los diferentes escenarios a simular se presentan en la Tabla 2, y corresponden a escenarios que la gerencia de operaciones ha identificado como posibles políticas futuras de producción.

Tabla 2
Escenarios a simular en el sistema modular de confección

Cada escenario se evaluará a través del cálculo del tiempo ocioso o tiempo perdido de los módulos de confección y de los equipos de montaje. Para formular el modelo de simulación que represente adecuadamente el sistema de confección modular, se acude al uso de las variables utilizadas por Cano, Campo y Gómez (2018), que se resumen en la Tabla 3.

Tabla 3
Variables utilizadas en el modelo de simulación

Fuente: Cano, Campo y Gómez (2018)

Una vez definidas las variables a utilizar en el modelo de simulación, se procede a elaborar el diagrama de flujo de avance por eventos que se presenta en la Figura 2, el cual explica el funcionamiento de la simulación por eventos desde un inicio hasta la obtención de los reportes que finalmente muestran el tiempo perdido en módulos de confección y en equipos de montaje.

Una vez se crea el diagrama de flujo de avance por eventos para el modelo de simulación, se procede a programar en Visual Basic Applications (VBA) la simulación para el sistema de confección modular, contando con el apoyo de una plantilla de Excel donde se realiza el ingreso de datos de entrada y el cálculo de variables aleatorias. Las variables de tiempo de montaje y tamaño de lote siguen una distribución uniforme, que está determinada por los valores mínimos y máximos expresados en la Tabla 2. Para el caso del tiempo de llegada entre lotes, se utiliza una distribución exponencial con un valor del parámetro l = 72,2 utilizado por Cano, Campo y Gómez (2018). En cada corrida de la simulación, la plantilla de MSExcel genera números aleatorios que a través de las funciones de distribución probabilidad inversa se convierten en observaciones aleatorias de los componentes del modelo del sistema de confección modular. De esta forma, se presenta en la Figura 3 el pseudocódigo en MSExcel - VBA para el modelo del sistema de confección modular.

Figura 2. Diagrama de flujo de avance por eventos

-----

Figura 3
Pseudocódigo en MSExcel - VBA para el modelo de simulación

Para ejecutar la simulación sobre cada uno de los escenarios planteados, se establecieron 100 corridas (simulaciones) por escenario, y cada simulación se ejecutó para un horizonte de tiempo de 1 semana, la cual se compone de 5.760 minutos laborales.

Al ejecutar el modelo de simulación en MSExcel – VBA en cada escenario, se obtuvieron 100 corridas, con las cuales se obtuvo valor promedio del tiempo perdido en módulos de confección y en equipos de montajes, permitiendo así calcular resultados que guíen la toma de decisiones sobre cómo configurar la planta de confección modular, satisfaciendo los requerimientos de la gerencia de operaciones de la empresa en estudio.

La Tabla 4 presenta los resultados de tiempos perdidos para módulos de confección y equipos de montaje para tamaños de lote grandes, que oscilan entre 1.200 y 1.600 minutos de producción; evidenciando que el balance de planta más apropiado corresponde al escenario 1 al tener 3 equipos de montaje, los cuales toman entre 3 a 5 horas para realizar el alistamiento y preparación de una referencia, generando así en una semana un promedio de 1.522 minutos perdidos en los módulos de confección y 193 minutos perdidos en los equipos de montajes. Igualmente, se observa que otro plan atractivo corresponde al escenario 5, al implementar 5 equipos de montaje que requieren de 4 a 8 horas para realizar el alistamiento y preparación de una referencia, generando así 323 minutos perdidos en los módulos de confección y 1.427 minutos perdidos en los equipos de montajes. Una de las diferencias entre estos dos escenarios radica en el tiempo por montaje, que en el escenario 1 implica la capacitación del personal de montajes en técnicas de cambios rápidos como el SMED (Single Minute Exchange of Die), y la implementación que nuevas herramientas y tecnologías que permitan reducir los tiempos de alistamiento y preparación. Adicional a esto, es importante notar que el escenario 1 y 5 generan un tiempo total perdido similar, pero en el escenario 1 es mayor el tiempo perdido en módulos, mientras que en el escenario 5 es mayor el tiempo perdido en los equipos de montaje.

Tabla 4
Tiempo perdido en módulos y montajes para tamaños de lote grandes

En el caso de la empresa en estudio, las preferencias del tomador de decisiones priorizan en minimizar el tiempo total perdido, y en especial reducir el tiempo perdido en módulos de confección, debido a que los módulos de confección utilizan un mayor número de empleados que los equipos de montaje, y debido a que los tiempos perdidos en los módulos de confección representan una reducción en la tasa de producción de la planta de confección.

Para tamaños de lote medianos, que toman entre 600 y 800 minutos su procesamiento en módulos de confección, se identifica en la Tabla 5 que el escenario 10 es el más apropiado para el balance de la planta, y consiste en 9 equipos de montaje, los cuales toman entre 4 a 6 horas para realizar el alistamiento y preparación de una referencia, generando así en una semana un promedio de 676 minutos perdidos en los módulos de confección y 1.628 minutos perdidos en los equipos de montajes. El segundo escenario más atractivo para este caso sería el escenario 11, con menor tiempo perdido en los equipos de montaje (506 minutos), pero con mayor tiempo perdido en los módulos de confección (6.017 minutos).

Tabla 5
Tiempo perdido en módulos y montajes para tamaños de lote medianos

Por otro lado, en la Tabla 6 se identifica que para lotes de tamaño pequeño (entre 400 y 530 minutos de producción), el escenario 12 es el más atractivo para la empresa en estudio, que consiste en 12 equipos de montaje con un tiempo de alistamiento y preparación entre 4 y 6 horas, debido a que genera el menor tiempo total perdido, con 1.676 minutos semanales perdidos en módulos de confección, y 3.845 minutos perdidos en equipos de montajes. A pesar de que el escenario 13 genera menor tiempo perdido en equipos de montaje, genera tiempos perdidos en módulos de confección significativamente mayores a los del escenario 12.

Tabla 6
Tiempo perdido en módulos y montajes para tamaños de lote pequeños

Con los resultados de la simulación se evidencia que dado un tamaño de lote, y un número de equipos de montaje, el tiempo perdido en los módulos de confección aumenta considerablemente a medida en que el tiempo de montaje de una referencia aumenta, y de forma contraria, disminuye considerablemente el tiempo perdido de los equipos de montajes. También se observa que dado un tamaño de lote y un tiempo estipulado para el montaje de una referencia, a medida en que aumentan los equipos de montaje se disminuye drásticamente los tiempos perdidos en los módulos de confección, mientras que aumenta el tiempo ocioso de los equipos de montaje.

Por otro lado, a medida en que disminuye el tamaño de lote promedio a procesar en la planta de confección, aumenta drásticamente el tiempo perdido en los módulos de confección, a pesar de que se aumente significativamente el número de equipos de montajes. Comparando los resultados del escenario 6 y del escenario 9, el tiempo perdido en módulos de confección aumenta en 32.701 minutos semanales al pasar de tamaños de lote grandes a tamaños de lote medianos, a pesar de contar con el mismo número de equipos de montaje y rango de tiempo para los alistamientos y preparaciones. Por otro lado, en este comparativo el tiempo ocioso de los equipos de montaje disminuye en 4.581 minutos semanales para el caso mencionado al pasar de tamaños de lote grandes a tamaños de lote medianos.

Analizando la comparación de los resultados del escenario 10 y escenario 12, y comparando los resultados del escenario 11 y escenario 13, donde en cada comparación se presenta el mismo rango para el tiempo de alistamiento y preparación, se observa que aumenta el tiempo total perdido y el tiempo perdido en módulos de confección al pasar de tamaño de lote medianos a pequeños, a pesar que se aumenta el número de equipos de montaje de 9 a 12 en ambas comparaciones.

Por lo tanto, para la empresa en estudio se recomienda trabajar en lo posible con el mayor tamaño lotes que permita el mercado, de manera que se disminuya el total de tiempo ocioso, y en especial el tiempo perdido en los módulos de confección. Adicional a esto, los resultados de la simulación permiten evidenciar que a medida en que se reduce el tamaño de lote, si se desea reducir los tiempos perdidos en módulos de confección y en equipos de montajes, debe priorizarse la reducción de los tiempos promedios de cada alistamiento y preparación, y luego pensar en incrementar el número de equipos de montaje.

En el caso en que la gerencia de operaciones no tenga definidas preferencias sobre las variables de entrada y salida del modelo simulación, se recomienda hacer uso del análisis envolvente de datos (DEA) sobre los resultados arrojados por la simulación (Cano, Campo, & Baena, 2017), de tal manera que se seleccione el escenario que ofrezca mayor eficiencia a la empresa de confección.

Finalmente, estos resultados demuestran que la simulación de eventos discretos permite orientar al tomador de decisiones sobre los posibles resultados en cuanto a tiempos perdidos en módulos y equipos de montaje, según las condiciones de operaciones deseadas, que están dadas por el número de equipos de montaje, tamaños de lote y tiempos de alistamientos y preparaciones.

Este artículo presenta una metodología que apoya el balanceo de capacidades y asignación de recursos en plantas de confección, con el fin de reducir los tiempos perdidos en módulos de confección y equipos de preparación y alistamiento. De esta forma, se desarrolló un modelo de simulación de eventos discretos en empresas con sistemas de confección modular, soportado en MSExcel – VBA, lo cual facilita la personalización de los modelos, la parametrización de una amplia cantidad de variables, y la inclusión de herramientas, metodologías cuantitativas y cualitativas a este tipo de modelos de simulación.

En este sentido, el fácil acceso a lenguajes de programación y hojas de cálculo permiten integrar modelos de simulación con plataformas informáticas de gestión empresarial previamente adquiridas o desarrolladas por las organizaciones (ERP, WMS, MPS, CRM, DRP, entre otros); potencializando y maximizando el uso de información disponible en cada empresa.

El modelo de simulación desarrollado brinda grandes ventajas a las empresas de confección y moda al permitirles experimentar y evaluar posibles escenarios teniendo en cuenta los cambios del mercado y mejoras los procesos, sin la necesidad de modificar realmente el sistema productivo, sin interrumpir el trabajo en planta, ahorrando así costos de tiempos improductivos, represamiento de producción, reprocesos e ineficiencias que se incurrirían en ensayos reales.

Para garantizar el éxito en el proceso de desarrollo y validación de modelos de simulación en sistemas de confección modular, se requiere la participación del personal estratégico, táctico y operativo involucrado en los procesos de planificación y producción, para garantizar que el comportamiento del modelo y los resultados arrojados por la simulación sean acordes a la realidad empresarial en estudio. Para la empresa en estudio, debido a sus prioridades en disminuir el tiempo total perdido, y en especial el tiempo perdido en módulos de confección, se recomienda desarrollar estrategias y proyectos en pro de disminuir los tiempos de alistamiento y montaje, minimizando los requerimientos de personal de montaje.

Finalmente, se recomienda de igual forma realizar un diseño de experimentos sobre el modelo planteado y los resultados obtenidos de la simulación, para identificar las variables de mayor impacto en el funcionamiento del sistema y cuantificar las relaciones que existen entre estas variables.

ABEND, J. (1999). The line between success and failure. Bobbin, 40(5), 48-52.

ALLAHVERDI, A., NG, C., CHENG, T., & KOVALYOV, M. (2008). A survey of scheduling problems with setup times or costs. European Journal of Operational Research, 187(3), 985-1032.

ANDREJIĆ, M., BOJOVIĆ, N., & KILIBARDA, M. (2016). A framework for measuring transport efficiency in distribution centers. Transport Policy, 45(1), 99-106.

ARANGO, M., CANO, J. A., & ALVAREZ, K. (2012). Modelos de sistemas mrp cerrados integrando incertidumbre. Revista EIA, 1(18), 61-76.

BONSIGNORIO, F., & MOLFINO, R. (2006). An object based virtual reality simulation tool for design validation of a new paradigmmanufacturing facility. IFIP International Federation for Information Processin, 220(0), 301-308.

BUZACOTT, J. (2004). Modelling teams and workgroups in manufacturing. Annals of Operations Research, 126(1-4), 215-230.

CANO, J. A., CAMPO, E. A., & BAENA, J. J. (2017). Application of DEA in international market selection for the export of goods. DYNA (Colombia), 84(200), 376-382.

CANO, J. A., GOMEZ, R. A., & SALAZAR, F. (2017). Routing policies in multi-parallel warehouses: an analysis of computing times. Revista Espacios, 38(51), 23. Recuperado de: http://www.revistaespacios.com/a17v38n51/17385123.html

CANO, J. A., PANIZO, C. A., GARCÍA, F. H., & RODRÍGUEZ, J. E. (2015a). Desarrollo de Estrategias Competitivas para la Industria del Carbón en Norte de Santander. Revista Espacios, 36(15), 5. Recuperado de: http://www.revistaespacios.com/a15v36n15/15361506.html

CANO, J. A., PANIZO, C. A., GARCÍA, F. H., & RODRÍGUEZ, J. E. (2015b). Estrategias para el mejoramiento la cadena de suministro del carbón en Norte de Santander, Colombia. Boletín de Ciencias de la Tierra, 1(38), 65-74.

CANO, J., CAMPO, E., & GÓMEZ-MONTOYA, R. (2017). International Market Selection Using Weighing and Monte Carlo Simulation. Polish Journal of Management Studies, 16 (2), 40-50.

CANO, J., CAMPO, E., & GÓMEZ, R. (2018). Simulación de eventos discretos en la planificación de producción para sistemas de confección modular. Revista Técnica de la Facultad de Ingeniería Universidad del Zulia, 41(1), 50-58.

GÓMEZ, R. A., CANO, J. A., & CAMPO, E. A. (2016). Selección de proveedores en la minería de oro con lógica difusa. Revista Venezolana de Gerencia (RVG), 21(75), 530-548.

GÓMEZ, R. A., ZULUAGA, A., & CANO, J. A. (2014). Utilización de simulación discreta como estrategia de aprendizaje de logística empresarial. Revista Teckne, 12(1), 34-46.

HILLIER, F., & LIEBERMAN, G. (2010). Introducción a la Investigación de Operaciones. México D.F.: McGraw-Hill.

KO, E. (2001). Quick response adoption process in the Korean apparel industry. Journal of the Textile Institute Part 1: Fibre Science and Textile Technology, 92(2), 56-62.

MCNALLY, P., & HEAVEY, C. (2004). Developing simulation as a desktop resource. International Journal of Computer Integrated Manufacturing, 17(5), 435-450.

RAMDASS, K., & PRETORIUS, L. (2011). Implementation of modular manufacturing in the clothing industry in Kwazulu- Natal: A case study. South African Journal of Industrial Engineering, 22(1), 167-181.

RAMESHBABU, V. (2006). Garment production systems - An overview. Textile Magazine, 47(9), 22.

ROJAS, M., GUISAO, E., & CANO, J. A. (2011). Logística Integral: Una propuesta práctica para su negocio. Medellín: Universidad de Medellín.

SALAZAR, F., GOMEZ, R. A., & CANO, J. A. (2017). El problema de carga de pallets en centros de distribución utilizando diseño de mezclas. Revista Espacios, 38(2), 2. Recuperado de: http://www.revistaespacios.com/a17v38n02/17380202.html

SARACHE, W., CESPÓN, R., IBARRA, S., & ALONSO, P. (2004). Modular manufacturing: An alternative to improve the competitiveness in the clothing industry. International Journal of Clothing Science and Technology, 16(3-4), 301-309.

WANG, J., SCHROER, B., & ZIEMKE, M. (1991). Understanding modular manufacturing in the apparel industry using simulation. Winter Simulation Conference Proceedings, (págs. 441-447). Phoenix, AZ, USA.

1. Universidad de Medellín, Colombia. Ingeniero Industrial, Magister en Ingeniería Administrativa. jacano@udem.edu.co

2. ESACS – Escuela Superior en Administración de Cadena de Suministro, Colombia. Ingeniero Industrial, Magister en Ingeniería Industrial. emiroa86@hotmail.com

3. Politécnico Colombiano Jaime Isaza Cadavid, Colombia. Ingeniero Industrial, PhD en Ingeniería, Industria y Organizaciones. ragomez@elpoli.edu.co