

 Vol. 39 (Nº 23) Año 2018. Pág. 28
Vol. 39 (Nº 23) Año 2018. Pág. 28
Liliana ENCISO 1; Elmer ZELAYA 2; Pablo Alejandro QUEZADA-Sarmiento 3
Recibido: 09/01/2018 • Aprobado: 28/01/2018
RESUMEN: En el presente trabajo se simuló el crecimiento del sauce ecuatoriano, sauce blanco o salix alba con las herramientas L-System y Vlab bajo plataforma Mac. Esta simulación es aplicada en el contexto educativo para explicar el uso medicinal que ha tenido esta planta. Así mismo se puede simular el crecimiento de otras plantas medicinales u ornamentales que existen en el Ecuador. Estas herramientas también pueden ser utilizadas en el campo de las matemáticas, programación entre otras ciencias. |
ABSTRACT: In this work the simulation the growth of the Ecuadorian willow, white willow or salix alba with the L-System and Vlab tools under the Mac platform was simulated. This simulation is applied in the educational context to explain the medicinal use of this plant. Likewise, it can simulate the growth of other medicinal or ornamental plants that exist in Ecuador. These tools can also be used in the field of mathematics, programming among other sciences. |
En la actualidad existen un sinnúmero de herramientas con las que se puede modelar la diversidad de comportamientos y procesos de nuestro entorno, sin embargo, muchos de ellos están orientados a conocer obligatoriamente un lenguaje de programación. El motivo de desarrollo de esta investigación fue reemplazar ese lenguaje de programación por herramientas dinámicas de modelado en la representación de figuras geométricas mediante funciones matemáticas, ángulos e iteraciones, así como también comportamientos biológicos como es el crecimiento de una planta (Muhamad, Zaman,& Ahmad, 2012), (Smith, 2015), (Zhu et al, 2017).
Este estudio del funcionamiento de la planta ha venido acompañado y apoyado por el desarrollo de una nueva familia de modelos llamados modelos funcionales - estructurales (Boudon, 2012). Estos modelos computacionales utilizan 3D en sus representaciones de la arquitectura de la planta para simular diferentes tipos de comportamientos físicos, fisiológicos, o procesos eco-fisiológicos, y que sea posible evaluar los efectos de estos procesos en el funcionamiento, desarrollo y forma (Bollig et al, 2007), (Rongier, Collon, & Renard, 2017).
Analizar la herramienta a fin de desarrollar la práctica en el tema de enjambres gramaticales, permite contemplar diferentes variables en su sintaxis, además brinda un alto nivel de modelado en diversos campos de la investigación.
El presente trabajo es una investigación tecnológica, donde se han analizado y simulado dos herramientas gramaticales a fin de validar el crecimiento de una planta que crece en el sur del Ecuador en los cuaces de los ríos de la ciudad de Loja. Las herramientas gramaticales fueron instaladas y ejecutadas en el entorno MacOSX versión 10.10.3.
Lindenmayer-sistemas o L-System, se introdujo como un modelo teórico de desarrollo de la planta (Lintermann & Deussen,1996). En el área informática L-System se convirtió en una poderosa herramienta para describir el comportamiento de las células vegetales y para la creación biológica de modelos visuales realistas de plantas, capaz de simular su crecimiento y la interacción con el medio ambiente (Prusinkiewicz & Lindenmayer, 1996), (Luisa et al, 2015). El sistema de Lindenmayer es un sistema de reescritura paralelo y un tipo de gramática formal compuesto por un conjunto reglas y símbolos, es utilizado para modelar el proceso de crecimiento de plantas y generar fractales de diferentes tipos. Es el más descrito en las investigaciones sobre enjambres gramaticales orientados a estas simulaciones.
L-System también se han utilizado para modelar la morfología de una variedad de organismos y se pueden utilizar para generar fractales auto-similares, tales como los sistemas de función iterados aplicados a diversos entornos educativos y de investigación (Durikovic, Kaneda, Yamashita, 1997), (Kaliakatsos-Papakostas, Floros, Vrahatis, 2012).
La mayor parte de estos sistemas tienen un interés investigativo, pero es innegable que también son usados para modelar y generar escenas realistas, así también en la cinematografía y el mundo de los videojuegos.
En la Figura 1, se muestra el entorno y componentes del sistema. Para manipularla se debe revisar cual es la gramática, sus reglas y el significado de cada variable. El entorno es muy amigable y fácil de manipular. El ejemplo generado se encuentra en la Figura 2, donde se ve claramente como el algoritmo permite el crecimiento y movimiento de la planta de acuerdo a un ángulo y el número de iteraciones durante su simulación.
Modelo de escenario aplicado a un entorno educativo:
Figura 1
Entorno de la herramientas L-System
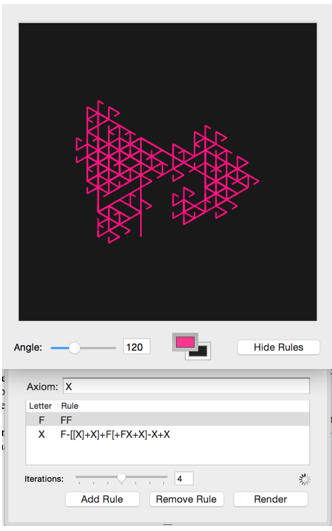
En la tabla 1, se muestra un alfabeto de símbolos que pueden ser utilizados para hacer cadenas apoyados en una colección de reglas de producción que se expanden a partir de una cadena inicial denominada "axioma" para empezar la construcción, y un mecanismo para la traducción de las secuencias generadas en las estructuras geométricas.
Tabla 1
Gramática de la herramienta L-System
Variable |
Significado |
F |
Se desplaza hacia adelante por la longitud de la línea dibujando una línea |
f |
Se desplaza hacia adelante por la longitud de la línea sin dibujar una línea |
+ |
Gire a la izquierda por el ángulo de 90º |
- |
Gire a la derecha por el ángulo de 90º |
! |
Sentido inverso (giro a 180 grados) |
[ |
Realiza un PUSH a la gráfica aplicando el estado de la pila |
] |
Realiza un POP a la gráfica aplicando el estado de la pila |
# |
Incrementa el ancho de línea por el ancho de línea incrementada |
! |
Decrementa el ancho de línea por la ancho de línea incrementada |
@ |
Dibuja un punto con el radio del ancho de línea |
{ |
Abre un polígono |
} |
Cierra un polígono |
> |
Multiplica la longitud de la línea por la escala del factor de la longitud de la línea |
< |
Divide la longitud de la línea por la escala del factor de la longitud de la línea |
& |
Cambia el significado de + y - |
( |
Decrementa el giro del ángulo por el giro del incremento del ángulo |
) |
Incrementa el giro del ángulo por el giro del incremento del ángulo |
Un alfabeto viene a ser una serie finita de elementos geométricos que son utilizados para realizar cadenas apoyados en reglas. Un axioma representa una secuencia determinada de símbolos del alfabeto definido en la Tabla I. Una regla recursiva es la sustitución de símbolos por axiomas.
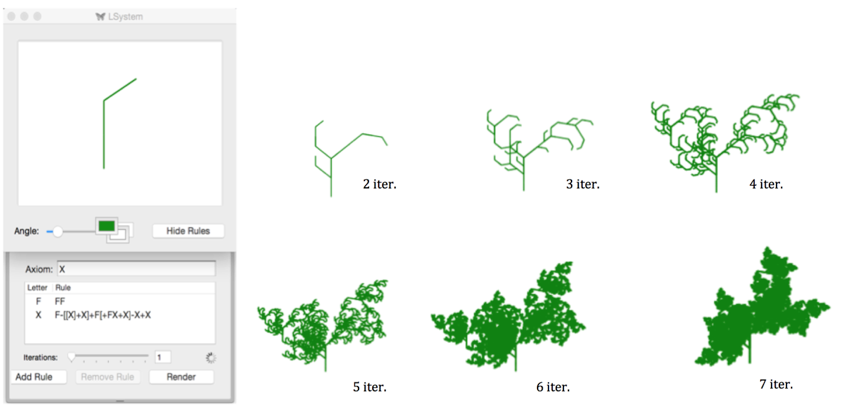
En la figura 2a, se muestra la presentación en la herramienta L-System del crecimiento del sauce ecuatoriano también conocido como sauce blanco o salix alba y en la figura 2b en la herramienta Vlab. Si se hace el análisis comparativo entre ambas herramientas, es notorio que la herramienta Vlab representa mejor el crecimiento de un sauce, tiene las ramas más dispersas tal y como en la realidad es. Esta simulación es aplicada en el contexto educativo para explicar el uso medicinal que ha tenido esta planta en la reducción de la sensación de dolor y, además de propiedades analgésicas, propiedades antiinflamatorias, y antipiréticas. Así mismo se puede simular el crecimiento de otras plantas medicinales a fin de que poner en conocimiento de los estudiantes, por un lado el crecimiento y por otro conocer la diversidad de plantas medicinales que existen en el Ecuador.
En L-System también se puede representar figuras geométricas y hacer giros en 3D. Esto puede ser aplicado al campo de las matemáticas. En la Figura 3 se observan líneas generadas en 60 grados inicialmente, y al ir modificando el ángulo se observa un cambio total en la representación gráfica.
Figura 2a
Resultados de la simulación del crecimiento del sauce en L-System
-----
Figura 2b
Resultados de la simulación del crecimiento del sauce en Vlab

-----
Figura 3
Resultados de generación de figuras geométricas en L-Systems
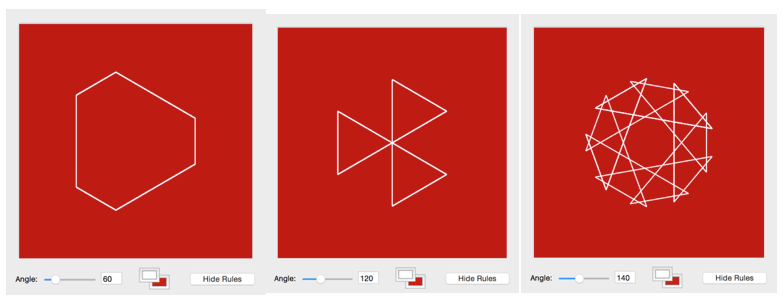
El L-System puede ser utilizado en entornos educativos para demostrar el comportamiento de los fractales. Como práctica en el ámbito matemático y educativo se representó la gráfica del triángulo de Sierpinski, donde un triángulo equilátero, se subdividió de forma recursiva en triángulos equiláteros pequeños, originalmente construido como una curva, representando a los conjuntos auto-similares. Es decir, es un patrón generado matemáticamente que puede ser reproducible en cualquier ampliación o reducción. Para representar la gráfica del triángulo de Sierpinski se han establecido las siguientes parámetros:
En la Figura 4., se muestra la simulación de este triángulo en diversas iteraciones mostrando el comportamiento de este patrón.
Figura 4
Triángulo de Sierpinski en L-Systems generado matemáticamente

También podemos realizar la simulación del crecimiento de todo tipo de plantas con la herramienta Vlab (ver figura 5a, figura 5b y figura 5c).
Figura 5
Simulación y visualización del crecimiento de una planta ornamental en 3D en Vlab.

L-System es muy sencillo y fácil de manipular por lo que permite establecer múltiples opciones de la gramática y generar diversos tipos de gráficos en diferentes entornos educativos y de investigación. Sin embargo tiene limitantes a la hora de procesar más de 7 iteraciones por objeto simulado. Por lo que se puede concluir que Vlab tiene mejores ventajas con respecto a L-System ya que su representación de los objetos demostrarían el fenómeno que se estudia, con un alto grado de realismo y fidelidad.
La herramientas L-System y Vlab pueden ser aplicadas en cualquier estructura, siempre que se logre identificar el patrón básico para su representación.
Boudon, F., Pradal, C., Cokelaer, T., Prusinkisrewicz, P. and Godin, C. (2012). “L-py: an l-system simulation framework for modeling plant development based on a dynamic language,” Frontiers in Plant Science, vol. 3, no. 76, 2012.
Durikovic, R.; Kaneda, K.; Yamashita, H. (1997). "Visual modeling of stomach growth on the basis of L-systems," in Shape Modeling and Applications, 1997. Proceedings., 1997 Interna-tional Conference on , vol., no., pp.121-128, 3-6 Mar 1997 doi: 10.1109/SMA.1997.634889. URL: http://ieeexplore.ieee.org/stamp/stamp.jsp?tp= &arnumber=634889&isnumber=13
Evan F. Bollig, Paul A. Jensen, Martin D. Lyness, Mehmet A. Nacar, Pedro R.C. da Silveira, Dan Kigelman, Gordon Erlebacher, Marlon Pierce, David A. Yuen, Cesar R.S. da Silva. (2007). VLAB: Web services, portlets, and workflows for enabling cyber-infrastructure in computational mineral physics, Physics of the Earth and Planetary Interiors, Volume 163, Issues 1–4, 2007, Pages 333-346, ISSN 0031-9201, https://doi.org/10.1016/ j.pepi.2007.03.005.(http://www.sciencedirect.com/science/article/pii/S003192010700 0544)
Guillaume Rongier, Pauline Collon, Philippe Renard. (2017). Stochastic simulation of channelized sedimentary bodies using a constrained L-system, Computers & Geosciences, Volume 105, 2017, Pages 158-168, ISSN 0098-3004
Kaliakatsos-Papakostas, M.A.; Floros, A.; Vrahatis, M.N. (2012). "Intelligent Generation of Rhythmic Sequences Using Finite L-systems," in Intelligent Information Hiding and Multimedia Signal Processing (IIH-MSP), 2012 Eighth International Conference on , vol., no., pp.424-427, 18-20 July 2012. doi: 10.1109/IIH-MSP.2012.109 URL: http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=6274273&isnumber=627 4114
Lintermann B. and Deussen, O. (1996). “Interactive modelling and animation of branching botanical structures,” in Computer Animation and Simulation ’96, ser. Eurographics, R. Boulic and G. Hegron, Eds. Springer Vienna, 1996, pp. 139–151. [Online]. Available: http://dx.doi.org/10.1007/978-3- 7091-7486-910
Luisa, M., et al. (2015). Modelo informático para la construcción de doseles virtuales de fresa. Revista mexicana de ciencias agrícolas, 2015, vol. 6, no 2, p. 291-302.
Murniza Muhamad, Halimah Badioze Zaman, Azlina Ahmad. (2012). Virtual Biology Laboratory (VLab-Bio): Scenario-Based Learning Approach, Procedia - Social and Behavioral Sciences, Volume 69, 2012, Pages 162-168, ISSN 1877-0428, https://doi.org/10.1016/j.sbspro.2012.11.395.(http://www.sciencedirect.com/science/article/pii/S187704281205 3815)
Prusinkiewicz P. and Lindenmayer A. (1996). The Algorithmic Beauty of Plants. New York, NY, USA: Springer-Verlag New York, Inc., 1996.
Smith, T. (2015). On infinite words determined by L systems, Theoretical Computer Science, Volume 595, 2015, Pages 1-10, ISSN 0304-3975
Yanhe Zhu, Dongyang Bie, Xiaolu Wang, Yu Zhang, Hongzhe Jin, Jie Zhao, A. (2017). Distributed and parallel control mechanism for self-reconfiguration of modular robots using L-systems and cellular automata, Journal of Parallel and Distributed Computing, Volume 102, 2017, Pages 80-90, ISSN 0743-7315
1. Doctora en Informática; Master en Ciencias de la Ingeniería; Máster en Ciencias y Tecnologías de la Computación; Ingeniería en Sistemas; Docente de la Universidad Técnica Particular de Loja, Investigadora del Grupo Innovación Tecnológica Educativa, lenciso@utpl.edu.ec
2. Profesional en Formación en Informática; Universidad Técnica Particular de Loja, erzelaya@utpl.edu.ec
3. Ingeniero en Informática y Multimedia, Máster en Ciencias y Tecnologías de la Computación, Docente de la Universidad Internacional del Ecuador Escuela de Informática y Multimedia, paquezadasa@uide.edu.ec