ISSN 0798 1015

Vol. 39 (Nº22) Año 2018. Pág. 34

Cartas de control para optimizar el proceso de pintura de láminas de aluminio

Control charts to optimize the process of painting on aluminum sheets

Luz Marcela RESTREPO Tamayo 1

Recibido: 03/02/2018 • Aprobado: 02/03/2018

Contenido

1. Introducción

2. Metodología

3. Resultados

4. Conclusiones

Referencias bibliográficas

1. Introducción

Las acciones orientadas a reducir los costos de calidad, enmarcados en costos de evaluación, de prevención, y de fallas internas y externas, pueden incrementar la competitividad y la productividad de los procesos (Chase, Jacobs, & Aquilano, 2009) (Rungtusanatham, 2000). Con base en lo anterior, la calidad debe gestionarse partir de un conjunto de actividades planeadas que permitan cumplir los requisitos de calidad del producto o servicio (Gutiérrez Pulido & De la Vara Salazar, 2009), y el Control Estadístico de Procesos (CEP) da cobertura a sus aspectos cuantitativos a partir de herramientas estadísticas (Deming, 1965) (Chase et al., 2009). CEP se define como “un conjunto poderoso de herramientas para resolver problemas, muy útil para conseguir la estabilidad y mejorar la capacidad del proceso mediante la reducción de la variabilidad” (Montgomery, 2009). De manera alternativa, CEP se puede definir como “el uso de herramientas y técnicas de base estadística principalmente para la gestión y mejora de los procesos” (Juran & Godfrey, 1998). Una de las herramientas dominantes del CEP es la Carta de Control, diseñada por Walter Shewhart, en la que se grafica en el tiempo una medida o un conteo de calidad (Caulcutt, 1995). Una carta de control se define como “la representación gráfica de una característica de calidad que se ha medido o calculado a partir de una muestra contra el número de muestra o tiempo" (Montgomery, 2009), o como “una secuencia temporal con líneas de decisión agregadas" (Ryan, 2000), de tal manera que la variabilidad de una característica de calidad puede ser analizada con base en la salida del proceso estimando los parámetros de su distribución estadística (Juran & Godfrey, 1998) (Stapenhurst, 2005) (Duncan, 1989).

La construcción de cartas de control tiene dos fases: en fase I se estiman los parámetros de la carta de control de manera iterativa hasta que el proceso se encuentra bajo control estadístico; en fase II se monitorea el estado de control estadístico del proceso a lo largo del tiempo (Bersimis, Psarakis, & Panaretos, 2007), y por ello se dice que en Fase II, una carta de control es una prueba de hipótesis que se repite en el tiempo para identificar si el proceso ha tenido variaciones que impliquen que ya no está bajo control estadístico (Woodall, 2000) (Bersimis et al., 2007).

En este artículo se presenta una aplicación de cartas de control en Fase I para monitorear el espesor de pintura de láminas de aluminio, y el impacto que su implementación tuvo en la optimización de la materia prima y en la disminución de reprocesos, evidenciando que la estadística industrial aún sigue vigente y es útil para las organizaciones(Banks, 1993).

Existen dos tipos generales de cartas de control: para variables y para atributos, que pueden ser univariadas o multivariadas. Las cartas de control univariadas para variables se aplican a características de calidad que se miden en una escala numérica (X; R; S; Individuales). Las cartas de control univariadas para atributos se aplican a características de calidad de tipo discreto, esto es, requieren solamente un conteo asociado con la ocurrencia de un evento particular (p; np; c; u) (Gutiérrez Pulido & De la Vara Salazar, 2009). La carta de control se deberá seleccionar de acuerdo al tipo de variable aleatoria que interese estudiar (Stapenhurst, 2005). Dado que el espesor de pintura es una variable aleatoria continua, se decidió utilizar cartas de control para variables X-R, haciendo uso de los requerimientos estadísticos de diseño.

2.1. Descripción del proceso

El recubrimiento de las piezas se lleva a cabo mediante los siguientes subprocesos: montaje en cadena transportadora, pretratamiento en túnel de lavado (predesengrase, desengrase, decapado, enjuague, fosfatado, sellado), secado en túnel a 200°C, aplicación de pintura electrostática en polvo en cabina automática (pistolas osciladoras y operación de refuerzo), curado en horno de polimerización a aproximadamente 320°C, desmontaje e inspección, y posteriormente almacenamiento. El diagrama de flujo correspondiente se presenta en la Ilustración 1 .

Ilustración 1
Diagrama de flujo, proceso de pintura, elaboración propia

La cabina automática consta de 10 pistolas osciladoras verticales, enumeradas de 1 a 10 y distribuidas como indica la Ilustración 2. Cada pistola tiene una unidad de control donde se establecen las presiones de aire y de polvo necesarias para la aplicación, y cada una de ellas recubre un área específica de la lámina. El equipo está diseñado para recubrir superficies planas, siendo necesario disponer de dos operarios que refuercen las áreas de las piezas cuyo diseño y geometría formen jaulas de Faraday.              

Ilustración 2
Ubicación de pistolas osciladoras en
cabina de pintura, elaboración propia

2.2. Diagnóstico

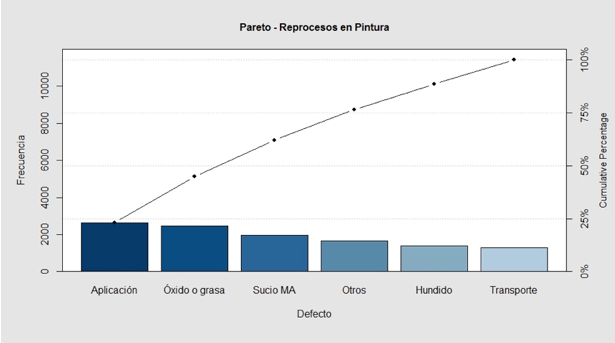
Con base en el análisis de la información de los reprocesos de Pintura, capturada en el transcurso de 5 meses, el reproceso que ocurre con mayor frecuencia (23.13%) es el denominado “Aplicación”, que incluye todas las piezas que no presentan un buen recubrimiento debido a fallas en las pistolas de la cabina automática o por errores en la operación de refuerzo. Lo anterior se puede evidenciar en el diagrama de Pareto construido usando la librería “qcc” de R, mostrado en la Ilustración 3 . En el diagrama se observan otros reprocesos como “Óxido o grasa”, asociado con un mal proceso de lavado (pretratamiento); “Sucio MA”, asociado a partículas del medio ambiente que ingresan a la cabina y contaminan la pintura de la pieza; en “Otros” se incluyen reprocesos por temperatura, ampollas, pintura contaminada, hervido, entre otros, cuyas frecuencias no son tan significativas para desagregarlas;  “Hundido” está asociado a problemas en el proceso de conformado de la lámina, previo a pintura; y “Transporte”, que está asociado a daños en la lámina pintada por su manipulación antes del proceso de ensamble.

Ilustración 3
Diagrama de Pareto - Reprocesos en Pintura

Además de considerar el número de reprocesos, se hizo seguimiento semanal durante 3 meses al rendimiento real de la materia prima en metros cuadrados pintados por kilogramo de pintura consumido, para los dos colores que más se utilizan: negro y almendra. Según el proveedor, el rendimiento debe ser de 13 m2/Kg para negro y de 11 m2/Kg para almendra, sin embargo, tal como se indica en la Tabla 1 , el rendimiento de la pintura para ambos colores se encuentra en promedio por debajo del estándar, incluso, por debajo de 10 m2/Kg. Por lo tanto, si las láminas tienen espesores altos o si se presentan reprocesos por aplicación debido a operaciones de refuerzo indebidas, el rendimiento de la materia prima disminuye, ya que se necesitan más kilogramos para pintar la misma área de lámina, lo que implica incurrir en costos adicionales de operación.

Tabla 1
Rendimiento semanal de pintura

2.3. Metodología

Debido a las características del proceso sólo se toman mediciones de espesores a aquellas piezas planas que no requieren refuerzo, los cuales reflejan el verdadero comportamiento del equipo. Las mediciones se realizan una vez las piezas salen del túnel de secado, seleccionando un punto específico de la lámina asociado a cada pistola automática, con el propósito de identificar si es necesario hacer ajustes en la presión de aire o de polvo, que puede ser modificada manualmente por los operarios.

Considerando el conocimiento del proceso, el costo de inspección y las variables incontrolables que afectan el espesor de la pintura de las piezas, se decidió utilizar un tamaño de muestra de 10 mediciones por pistola. La frecuencia de muestreo depende del flujo de producción de piezas planas, pero debido a que éste no es constante, se tuvo en cuenta el tiempo de reacción para realizar ajustes al proceso: el tiempo que hay entre la aplicación de la pintura y la medición del espesor es de aproximadamente 10 minutos, y el tiempo que tarda desmontar las 10 piezas y realizar las mediciones es de aproximadamente 3 minutos, por lo que se definió tomar muestras cada 15 minutos. El punto donde se toma el espesor corresponde al punto medio del área que recubre cada una de las pistolas automáticas, cada semielaborado es escogido de manera aleatoria, y las observaciones se realizaron bajo condiciones de operación similares.

Se tomaron alrededor de 40 muestras para el color almendra y 65 muestras para el color negro, con las cuales se construyeron las cartas de control por pistola utilizando la librería “qcc” de R. Para la construcción de la carta de medias y rangos se definió utilizar como amplitud de los límites el valor de 3, ya que da buenos resultados en la práctica y es el valor recomendado cuando no se tiene una implementación previa de Control Estadístico de Procesos. Para la carta de medias con límites tres sigma, se tiene que la probabilidad de error tipo I (α) es de 0.0027, lo que significa que se espera que cada 370 muestras se genere una falsa alarma de que el proceso está fuera de control (Gutiérrez Pulido & De la Vara Salazar, 2009)(Montgomery, 2009)(Duncan, 1989)(Ryan, 2000)(Evans & Lindsay, 2008)(Juran & Godfrey, 1998)(Stapenhurst, 2005)(Ryan, 2000). La Tabla 2 muestra las cartas de control de medias y rangos obtenidas para el color almendra. Las cartas de control para el color negro son omitidas.

Tabla 2
Cartas de control de rangos y medias por pistola – Almendra

3.1. Análisis del proceso

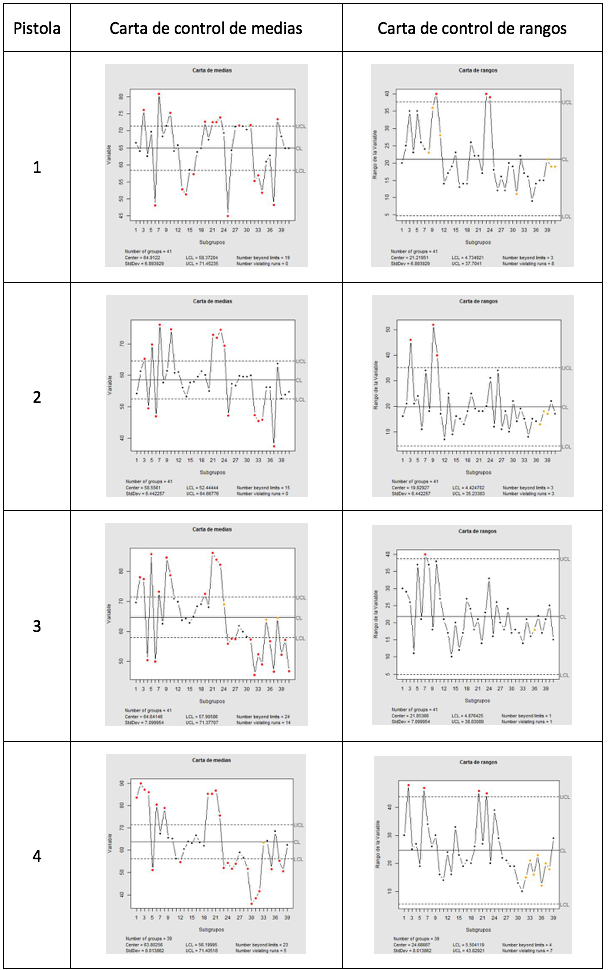
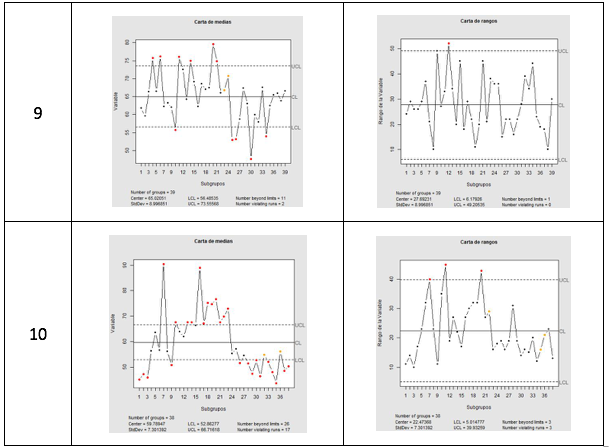
Las cartas de control para el color almendra y para el color negro, evidencian presencia de patrones de comportamiento no aleatorio en la variable “Espesor de pintura”, por lo que el proceso no está bajo control estadístico, además, chequeando los límites de control, tampoco está cumpliendo especificaciones, así que no se procede a hacer análisis de capacidad (Gutiérrez Pulido & De la Vara Salazar, 2009). Con base en la información registrada en la captura de datos, fue posible identificar las causas de los patrones de comportamiento no aleatorio, así que se decidió intervenir el proceso desde varios frentes para disminuir la variabilidad del proceso y acercarlo al cumplimiento de especificaciones.

Considerando que en el proceso interviene el factor humano, se diseñó internamente una capacitación sobre manipulación de la cabina automática de pintura (cuadro de mando de pistolas automáticas y unidad de control de refuerzo) y sobre conceptos técnicos de aplicación de pintura electrostática.

Debido a que el espesor es afectado por muchas variables incontrolables, se realizaron pruebas de hipótesis para analizar los ajustes que se hacen al equipo de aplicación de pintura, con el objetivo de indicar los valores de las presiones de aire y polvo (expresados en bares) para cada pistola y para cada color que garantice un recubrimiento entre las especificaciones. Se considera como tratamiento a aquella combinación de presiones de polvo y aire específicas de uso común en la operación; para cada pistola se tomaron los dos tratamientos más repetitivos, y el interés se concentra en identificar si existe o no diferencia significativa entre los espesores promedio que genera cada uno de los tratamientos, por lo que se utilizó pruebas de hipótesis para el valor medio con varianza desconocida, con un nivel de confianza del 95%.

Realizando los cálculos debidos, se obtuvieron los siguientes resultados:

• Un cambio de dos bares en la presión de polvo conservando la presión de aire genera un mismo espesor promedio.
• Un cambio de cuatro bares en la presión de polvo conservando la presión de aire genera un cambio directamente proporcional significativo en el espesor promedio.
• Una disminución de 2 bares en el polvo y un aumento de 2 bares en el aire genera espesores promedio estadísticamente diferentes
• Una disminución de dos bares en la presión de polvo conservando la presión de aire (siendo esta mayor en dos bares) genera un espesor promedio inferior.

En la Tabla 2 se presentan los valores a los cuales debe trabajar el equipo, para cada color y de uso generalizado para todas las piezas, considerando una tolerancia de más o menos 0.1 bar.

Tabla 3
Parametrización del equipo de aplicación de pintura, por pistola y por color

Ahora, considerando que la operación de refuerzo es uno de los factores que genera más reprocesos y variabilidad, se diseñó un instructivo que indica el área específica de refuerzo para cada tipo de pieza, definiendo para cada color las presiones de aire y polvo que debe utilizar el operario, considerando la gravedad específica de cada pintura y su respectivo poder cubriente. Complementario a lo anterior, se analizó la información histórica de las piezas reprocesadas por falta de refuerzo, se identificaron los más recurrentes y se inició un plan de seguimiento, en el cual se concluyó que el montaje de los mismos no permitía una adecuada aplicación de la pintura en las áreas asignadas. Para cada una de las piezas críticas, se hicieron las pruebas respectivas reduciendo dos unidades por conjunto de piezas a pintar durante un período de 2 semanas, evidenciando una disminución del 70% de las unidades reprocesadas.

En fase I, es necesario continuar tomando datos e identificar causas asignables de variación hasta que el proceso esté bajo control estadístico para iniciar fase II, sin embargo, el proceso aún no se ha estabilizado, así que la definición de los límites de control sigue en construcción. A pesar de lo anterior, se ha realizado seguimiento al rendimiento de materia prima, y durante un periodo de 12 semanas, se observó que el rendimiento promedio del color negro estaba en 10,62 m2/Kg y el rendimiento promedio del color almendra estaba en 10,86 m2/Kg, lo que sugiere una mejor utilización de la materia prima que se evidenció con un sobrante de 7,6% en el inventario de pintura.

En este artículo se presenta la fundamentación teórica del Control Estadístico de Procesos (CEP) y una aplicación de cartas de control de medias y rangos para analizar el comportamiento de la variable “Espesor de pintura” en láminas de aluminio, para los dos colores que más se aplican, haciendo uso de la Estadística Industrial para identificar oportunidades de mejora en el proceso de aplicación de pintura. Se identifica que el proceso está fuera de control estadístico y se pone en implementación un plan de acción que permite disminuir las unidades reprocesadas y aumentar el rendimiento de la materia prima.

Banks, D. (1993). Is Industrial Statistics Out of Control? Statistical Science, 8(4), 356–377. https://doi.org/DOI 10.1214/ss/1177010778

Bersimis, S., Psarakis, S., & Panaretos, J. (2007). Multivariate statistical process control charts: An overview. Quality and Reliability Engineering International, 23(5), 517–543. https://doi.org/10.1002/qre.829

Caulcutt, R. (1995). The Rigths and Wrongs of Control Charts. Journal of the Royal Statistical Society. Series C, 44(3), 279–288.

Chase, R. B., Jacobs, R. F., & Aquilano, N. J. (2009). Administración de Operaciones. Producción y Cadena de Suministros (12th ed.). México D.F.: Mc Graw Hill.

Deming, W. E. (1965). Principles of Professional Statistical Practice. The Annals of Mathematical Statistics, 36(6), 1883–1900.

Duncan, A. (1989). Control de Calidad y Estadística Industrial (5th ed.). México D.F.: Alfaomega.

Evans, J. R., & Lindsay, W. M. (2008). Administracion y control de la calidad.

Gutiérrez Pulido, H., & De la Vara Salazar, R. (2009). Control Estadístico de Calidad y Seis Sigma. (M. Hill, Ed.) (2th ed.).

Juran, J. M., & Godfrey, A. B. (1998). Juran’s Quality Control Handbook. McGrawHill. https://doi.org/10.1108/09684879310045286

Montgomery, D. (2009). Introduction to Statistical Process Control. (J. W. & Sons, Ed.) (6th ed.).

Rungtusanatham, M. (2000). The quality and motivational effects of statistical process control. Journal of Quality Management, 4(2), 243–264. Retrieved from http://dx.doi.org/10.1016/S1084-8568(99)00015-2

Ryan, T. (2000). Statistical Methods for Quality Improvement (2nd ed.). New Yotk: John Wiley & Sons.

Stapenhurst, T. (2005). Mastering Statistical Process Control. Zhurnal Eksperimental’noi i Teoreticheskoi Fiziki. Retrieved from http://scholar.google.com/scholar?hl=en&btnG=Search&q=intitle:No+Title#0%5Cnhttp://books.google.com/books?hl=en&lr=&id=6ct3TtP36YQC&oi=fnd&pg=PP2&dq=Mastering+Statistical+Process+Control&ots=-2bbz6cC6E&sig=EDXo4XFVoUf3cKVvg1Uznw9M7ms

Woodall, W. (2000). Controversies and Contradictions in Statistical Process Control. Journal of Quality Management, 32(4), 341–350.

1. Docente Faculta de Ingenierías. Universidad de Medellín. Ingeniera Industrial. Magíster en Estadística. lmrestrepo@udem.edu.co