

Vol. 39 (Nº 19) Año 2018 • Pág. 3
Roberto HERRERA Acosta 1; Kevin PALOMINO Pacheco 2; Fabiola REYES Jiménez 3; Guillermo VALENCIA Ochoa 4
Recibido: 08/01/2018 • Aprobado: 01/02/2018
RESUMEN: Considerando el significativo potencial de generación de energía eólica disponible en la región Caribe Colombiana, se hace necesario desarrollar estudios de caracterización de la velocidad y dirección del viento para el apropiado diseño de parques eólicos. Tomando las mediciones horarias realizadas por la estación meteorológica ubicada en la Universidad del Atlántico, se realizó un análisis estadístico e inferencial de los datos, el cual permitió caracterizar estadisticamente el comportamiento del viento, mediante gráficos de línea, medidas de tendencia central, estimaciones variacionales para interpretar los datos. También se analizó la velocidad del viento ajustada a la distribucion de probablidad indicada y se compararon las variables mediante tablas de contingencia. Finalmente, a partir de los resultados se evidenciaron patrones de comportamiento local y variacional, ademas de confirmar un fenomeno estacional. |
ABSTRACT: Considering the significative wind energy potential available in the Colombian Caribean Region, is necessary to conduct caracterizing study of wind speed and direction to the proper design of wind farm. Taking the hourly measurements made by the meteorological station located at the Universidad del Atlántico, a statistical and inferential analysis of the data was carried out, which allows to characterize the wind behavior by mean of the line graphs, central and variational estimation to intepretate the datas. The wind speed adjusted to the indicated probability distribution was also analyzed and the variables were compared using contingency tables. Finally, from the measurements were evidenced local patterns and variational behavior, also confirming a stational phenomenon. |
La energía eólica es una energía renovable socialmente beneficiosa, económicamente competitiva y respetuosa con el medio ambiente. Su uso ha aumentado rápidamente en todo el mundo en las últimas décadas. [1] En el parque eólico se aprovecha la energía cinética del viento para generar la energía eléctrica, la potencia de un aerogenerador depende fundamentalmente de la velocidad del viento, del área que abarcan las aspas y de un coeficiente propio de cada aerogenerador. [2]
El viento está sujeto a cambios de presión lo cual hace que las masas de aire se desplacen horizontalmente de una zona a otra más cercana con distinta presión, originándose así, el viento como un proceso estocástico, en donde se comporta de forma aleatoria, por tal razón, se hace necesario la utilización de análisis estadísticos descriptivos e inferenciales, de manera que permita organizar, presentar y describir el comportamiento de la velocidad y dirección del viento, como también, el tipo de distribución que corresponde a las variables, y de esta forma construir un modelo que represente el objeto de estudio. Estudios tratan de brindar información confiable con respecto a la proyección de la velocidad y dirección del viento, en donde se explora el comportamiento del viento a partir de unas variables independientes meteorológicas, tales como, humedad, radiación, temperatura, presión. De manera general se observa la existencia de un impacto de estas variables sobre el viento y su dirección. [3] [4]
La caracterización estadística de la velocidad y dirección del viento ha sido ampliamente estudiada por varios investigadores alrededor del mundo. Para el año 2015, Z.R. Shu presentó un análisis estadístico de las características del viento y del potencial de la energía eólica en sitios típicos de Hong Kong a partir de datos de viento de seis años registrados en cinco estaciones meteorológicas con diferentes condiciones de terreno, mediante la ayuda del modelo de distribución de Weibull. Las variaciones de la velocidad media del viento, así como los parámetros de Weibull, se destacaron en varias escalas de tiempo. El mayor parámetro de la escala de Weibull se observó en la cima de una colina, mientras que el más bajo se encontró en un sitio urbano. La variación mensual de la densidad de energía eólica fue presentada y discutida para cada sitio. Hilltops y islas costa afuera demostraron prominente mayor densidad de la energía eólica que áreas urbanas. Por lo tanto, se indicó que las colinas y las islas costeras son los lugares más prometedores para la explotación de la energía eólica en Hong Kong. [5] En ese mismo año, el Doctor Nurulkamal Masseran nos planteó que la potencia media no describe bien las características de la densidad de potencia. Por lo tanto, al conocer información sobre otras propiedades estadísticas, tales como desviación estándar, asimetría y curtosis, se puede obtener una mejor comprensión de las características y propiedades de la densidad de potencia. Su estudio propuso un método para derivar un modelo de densidad de energía eólica y sus propiedades estadísticas. La aplicación del método de transformación y la integración de Monte Carlo se ha discutido para abordar la dificultad de encontrar las diferentes propiedades estadísticas de la densidad de potencia. Además, una aplicación del método propuesto es demostrada por un estudio de caso que involucra datos de velocidad del viento de varias estaciones en Malasia. [6]
En el año 2016, Ozay y Soner publicaron un estudio realizado en una región de Turquía en el cual analizaban los datos de velocidad y dirección del viento de septiembre de 2008 a marzo de 2014 obtenidos de una estación de viento. Como resultado, la distribución de frecuencia de la velocidad del viento, las tendencias de la dirección del viento, la velocidad media del viento y la forma y escala de los parámetros Weibull han sido calculados para la región. El análisis sugiere que las velocidades del viento más altas que van de 6 a 12 m/s son frecuentes entre los sectores 340-360 °. Velocidades de viento más bajas, de 3 a 6 m/s ocurren entre sectores de 10-29 °. [7] Paralelamente, los investigadores Wang, Hu y Ma, proporcionaron un estudio exhaustivo basándose en los datos recopilados de cuatro estaciones de China central, en el cual revisaron y compararon los modelos paramétricos y no paramétricos para la distribución de probabilidad de velocidad del viento y los métodos de estimación para los parámetros de estos modelos (los métodos ampliamente utilizados y el algoritmo de optimización heurística estocástica). Las simulaciones revelaron que el modelo no paramétrico supera a todos los modelos paramétricos seleccionados en términos de precisión de ajuste y simplicidad operacional, y el algoritmo de optimización heurística estocástica es superior a los métodos de estimación ampliamente utilizados. [8]
En lo que va del año 2017, Xiangyun Qing presentó un análisis estadístico de las características eólicas de la isla de Santiago, Cabo Verde utilizando la velocidad histórica del viento y los datos de potencia del parque eólico de Santiago del año 2014. Una distribución de dos parámetros de Weibull se aplicó primero para modelar las velocidades del viento en varias escalas temporales y determinar el potencial de la energía eólica en la isla. El gobierno ha puesto en marcha un objetivo ambicioso, cubrir el 50% de electricidad a partir de energías renovables para el año 2020. Aunque la tasa media anual de penetración de la energía eólica ha alcanzado el 24% de la producción total de electricidad generada, elevar el nivel de penetración de la energía eólica en el futuro planteará numerosos desafíos para el funcionamiento y control del sistema eléctrico debido a la intermitencia inherente del viento. Los resultados de este estudio contribuyen a evaluar el potencial eólico de Cabo Verde para los inversores y pueden utilizarse para cuantificar las incertidumbres de la generación de energía eólica para el operador del sistema eléctrico. [9] Por otro lado, siguiendo con el tema, varios investigadores presentaron un estudio basándose en mediciones de las características del viento realizadas en la parte costera y continental de Lituania, en el que analizaron la aplicación de las metodologías de la distribución de probabilidad de Weibull al resumir la densidad de la energía eólica en lugares seleccionados. La función de densidad de probabilidad de Weibull se ha analizado mediante ocho métodos. Para la evaluación de la fiabilidad de la metodología, se calculó el error cuadrático medio, el coeficiente de determinación, la prueba de ji cuadrado y el error relativo. Se ha determinado que muchos métodos de cálculo de la función de densidad de probabilidad permiten obtener resultados bastante fiables. Sin embargo, dependiendo de la ubicación geográfica de la zona, la altura desde el nivel del suelo y la influencia de otros factores en la densidad de la energía eólica, algunos métodos no son aceptables, ya que dan grandes errores relativos. El modelo propuesto podría ser utilizado con éxito para encontrar los lugares adecuados para el desarrollo de la energía eólica en regiones que tiene el entorno similar. [10]
Con lo anterior, podemos inferir que hoy en día existe una necesidad a nivel mundial de encontrar alternativas para obtener energía renovable y es preciso estudiar la información real suministrada por estaciones meteorológicas. El principal aporte de este artículo es el estudio estadístico de los datos adquiridos en la Costa Caribe Colombiana, el cual es necesario, verás y confiable. Este informe servirá de base para desarrollar un futuro estudio de factibilidad, y confirmar la posibilidad de construir un parque eólico de generación eléctrica en la zona.
En este apartado se presentan los fundamentos matemáticos utilizados para desarrollar el análisis estadístico descriptivo e inferencial, ademas de las especificaciones de los sensores utilizados y ubicación de la estación meterologica.
Instalados en la estación meteorologica de la Universidad del Atlántico, se utilizó el sensor 03002 R. M. Young y el anemómetro 03101 para medir la velocidad y dirección del viento, el pirómetro CS300 para la radiación, el sensor CS106 para la presión barométrica y una sonda CS215 para medir la temperatura y humedad relativa, todos de la marca Campbell Científica.
Figura 1
Estación Meteorológica de la Universidad del Atlántico

Se emplean cuando es necesario representar las tendencias de una serie de datos, y éstos son numerosos o continuos; los gráficos de línea pueden cubrir períodos de minutos, horas, días, semanas, meses o años.



En este apartado se analiza el comportamiento de la velocidad del viento mediante la distribución de probabilidad que más se ajuste. Luego se busca si existe alguna relación de dependencia entre la velocidad y dirección del viento con las variables independiente, además cuantificar la magnitud de la relación de dependencia usando una metodología de tablas de contingencia.



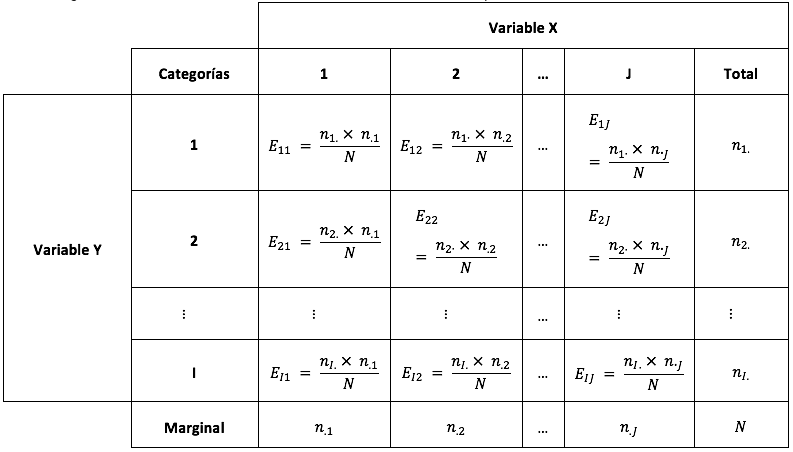
Tabla 1
Frecuencias esperadas de una tabla de contingencia
 '
'
Resultados de Gráficos
Conforme a la Figura 2 de secuencia, se observa de manera descriptiva que los datos correspondiente a la velocidad del viento no tiene un comportamiento tendencial , lo que supone, una posible estacionariedad, además no se encuentra una estacionalidad observable.
Figura 2
Secuencia de la velocidad del viento. Fuente propia

Analizando la Figura 3 de secuencia de la dirección del viento, se infiere de manera descriptiva que la dirección no presenta alguna tendencia ni estacionalidad observable, lo que supone, una posible estacionariedad de la variable.
Figura 3
Secuencia de la dirección del viento. Fuente propia

Resultados medidas de tendencia central, variabilidad y forma
Mediante la ecuación 1 se calcula la media de la velocidad y dirección, la cual registra en general una velocidad de 4,208 m/s y una dirección promedio de 0,053°, lo cual muestra que en promedio la velocidad se encuentra por encima del umbral requerido (2,794), sin embargo en el mes de octubre la velocidad se sitúa debajo del límite de especificación. Haciendo uso de la ecuación 4, se calcula la desviación de los datos, los cuales registran valores inferiores a 2 aproximadamente para las variables dirección y velocidad del viento, lo que significa que se encuentra poca variabilidad entre los datos, además cabe resaltar que el mayor máximo de velocidad fue de 9,520 m/s y el menor valor de 0,201 m/s.
Con la ecuación 5 se encuentra la asimetría de los datos suministrados, en donde como resultado se obtuvo que para la variable dirección, en general, la distribución es asimétrica positiva, mientras que, para la velocidad del viento, en los meses de octubre y febrero la distribución es asimétrica positiva, pero en los meses de diciembre y enero la distribución es asimétrica negativa. Utilizando la ecuación 6, se calcula la Curtosis de los datos, en donde para la dirección del viento corresponde a una distribución leptocúrtica, por otra parte, la velocidad tiene una distribución leptocúrtica en los meses de octubre y diciembre, pero tiene una distribución platicúrtica para los meses de enero y febrero, lo que significa que se detecta una mayor variabilidad en eso dos últimos meses, esto es debido a los diferentes cambios que tiene el viento para esa temporada.
Resultados distribución de probabilidad
Mediante la ecuación 8 se alcanza la máxima log verosimilitud para las distribuciones: Normal, Logística, Weibull, Laplace, Uniforme, Gamma y Exponencial. En donde, para el caso de la velocidad del viento se observa que la máxima probabilidad para la función densidad es una distribución Normal. posteriormente se contrasta el test de Kolmogorov a un nivel de confianza de 99%, en el cual se observa que todas las distribuciones son menores que el P- valor, por lo tanto, no se tiene suficiente evidencia estadística para decir que los datos se ajustan a una distribución específica, puesto que el valor P más pequeño entre las pruebas realizadas es menor que 0,01, sin embargo según los estudios realizados en Argelia, India, Arabia Saudita y Estados Unidos utilizan las distribución de Weibull y Gamma con la distribución de probabilidad de la velocidad del viento, por tal motivo, al no tener suficiente evidencia para determinar una la distribución que más se ajusta a los datos se toma la distribución Weibull y Gamma para su análisis. Para el caso de la dirección del viento la distribución que alcanza la máxima log verosimilitud es la Laplace y Logística. [11][12][13][14]
Los parámetros de las distribución que más se ajustan a los datos de velocidad del viento se encuentran en la Tabla 2, la forma (a) y la escala (b) de la distribución Weibull. En la Tabla 3 se especifican los parámetros de las distribución a los datos de dirección del viento, en donde, la distribución Laplace viene determinada por dos parámetros, uno de situación (a) y otro de escala (b).
Tabla 2
Parámetros de las distribuciones de probabilidades de la velocidad del viento.

Fuente propia
-----
Tabla 3
Parámetros de las distribuciones de probabilidades de la dirección del viento.

Fuente propia
Con respecto a la probabilidad acumulada de las diferentes distribuciones de probabilidad de la velocidad del viento, en particular, se tiene que la es de 28,12% para el caso de la distribución Weibull lo que significa que el 71,88% de las veces la velocidad se encontrara por encima de 2,794 m/s. Para la dirección del viento, la distribución de Laplace la que más se ajusta, entonces la probabilidad de que la dirección se más alta de 0,0441° es de 69,82%.
Resultados tablas de contingencia
En el análisis de la velocidad y dirección del viento, se observa en la Tabla 4 hay un mayor número de observaciones que presentan un valor superior a 2,794 m/s para la velocidad del viento y menor que el promedio de su dirección, lo que equivale a un 77,90% de observaciones situadas sobre el límite de especificación. Caso contrario sucede para valores mayores al promedio de dirección del viento, en donde el porcentaje de observaciones por encima de 2,794 m/s cae al 15,06 %. Además, mediante el estadístico Chi-Cuadrado de Pearson , con p<0.1, se rechaza la hipótesis nula, significa que la velocidad y dirección del viento tienen una relación de dependencia estadísticamente significativa. En cuanto a la Coeficiente PHI se observa que hay una relación moderada y directamente proporcional.
Tabala 4
Repercusión de la velocidad del viento en su dirección.

Chi-cuadrado=701,741; gl= 1; sig. Asintótica=0,000; Phi=-0,278
Fuente propia
Con respecto a la velocidad y las demás variables explicativas: Temperatura, Humedad Radiación y Presión. Las observaciones mayores a 2,794 m/s, en general, tienen mayor participación cuando las variables independientes son menores que su promedio, salvo humedad en el cual ocurre caso contrario, además, conforme a la frecuencia esperada, en todos los casos de velocidad por encima de su umbral las frecuencias observadas superan a la frecuencia esperadas, lo que significa que hay un mejor rendimiento de la velocidad por encima de 2,794 m/s.
La velocidad con respecto las variables independientes muestra mayor proporción cuando es superior a su límite de especificación, obteniendo aproximadamente 3 veces mayor su porcentaje que cuando está por debajo de su umbral. El valor Chi-cuadrado de Pearson es estadísticamente significativo para todas las variables independientes, con p<0.5, Esto significa que la velocidad del viento y las variables independientes tiene relación estadísticamente significativa de dependencia, es decir, se rechaza la hipótesis nula. En cuanto al Coeficiente PHI se observa que hay una relación moderadamente baja para todas las variables estudiadas y directamente proporcional para humedad mientras que para radiación, presión y temperatura es inversamente proporcional.
Frente al análisis de la dirección del viento y las variables independientes, se encuentra que se alcanza una mayor proporción de frecuencias observadas cuando la dirección está por debajo de su promedio independientemente de la ubicación de las variables explicativas, además, en promedio el porcentaje de observaciones superiores a media para ambas variables es de 56,9%. El valor Chi-cuadrado de Pearson es estadísticamente significativo para todos las variables menos la presión, con p<0.1, Esto significa que la dirección del viento y las variables independientes tienen una relación estadísticamente significativa de dependencia, es decir, se rechaza la hipótesis de independencia. Coeficiente PHI se observa que hay una relación moderadamente baja y directamente proporcional para la temperatura y radiación mientras que para la humedad y presión es inversamente proporcional.
Al analizar de manera descriptiva e inferencial el comportamiento de la velocidad y dirección del viento se observó gráficamente su variación en función del tiempo, tales son los casos que en algunos periodos se ubicaban por encima de 4m/s, además se determinó un 78% de probabilidad de obtener una velocidad por encima de 2,74 m/s, lo que significa que estadísticamente hay una alta probabilidad de obtener alto potencial de energía.
Los autores agradecen a la Universidad del Atlántico por el apoyo brindado a la presente investigación, principalmente en el proceso de adquisicion de la información de la estación meteorológica.
[1] G. Ren, J. Liu, J. Wan, Y. Guo, D. Yu, y J. Liu, “Measurement and statistical analysis of wind speed intermittency”, Energy, vol. 118, pp. 632–643, 2017.
[2] E. e O. U. Xunta de Galicia Consellería de Cultura, “3o ESO | IES Félix Muriel”, 2013. [En línea]. Disponible en: http://www.edu.xunta.gal/centros/iesfelixmuriel/node/706. [Consultado: 14-jun-2017].
[3] G. Valencia Ochoa y M. Vanegas Chamorro, Atlas eólico de la costa Caribe, Sello Edit. Barranquilla, 2016.
[4] A. M. Tafur García y A. D. Pizza Espitia, “Modelación y evaluación del potencial eólico como una fuente de generación de energía eléctrica en la zona costera de Cartagena.”, Universidad de Cartagena, 2013.
[5] Z. R. Shu, Q. S. Li, y P. W. Chan, “Statistical analysis of wind characteristics and wind energy potential in Hong Kong”, Energy Convers. Manag., vol. 101, pp. 644–657, 2015.
[6] N. Masseran, “Evaluating wind power density models and their statistical properties”, Energy, vol. 84, pp. 533–541, 2015.
[7] C. Ozay y M. S. Celiktas, “Statistical analysis of wind speed using two-parameter Weibull distribution in Alaçatı region”, Energy Convers. Manag., vol. 121, pp. 49–54, 2016.
[8] J. Wang, J. Hu, y K. Ma, “Wind speed probability distribution estimation and wind energy assessment”, Renew. Sustain. Energy Rev., vol. 60, pp. 881–899, 2016.
[9] X. Qing, “Statistical analysis of wind energy characteristics in Santiago island, Cape Verde”, Renew. Energy, 2017.
[10] V. Katinas, M. Marčiukaitis, G. Gecevičius, y A. Markevičius, “Statistical analysis of wind characteristics based on Weibull methods for estimation of power generation in Lithuania”, Renew. Energy, vol. 113, pp. 190–201, 2017.
[11] J. L. Torres, A. García, M. De Blas, y A. De Francisco, “Forecast of hourly average wind speed with ARMA models in Navarre (Spain)”, Sol. Energy, vol. 79, núm. 1, pp. 65–77, jul. 2005.
[12] T. B. M. J. Ouarda et al., “Probability distributions of wind speed in the UAE”, Energy Convers. Manag., vol. 93, pp. 414–434, 2015.
[13] B. K. Saxena y K. V. S. Rao, “ScienceDirect Estimation of wind power density at a wind farm site located in Western Rajasthan region of India”, Procedia Technol., vol. 24, pp. 492–498, 2016.
[14] M. Benatallah y M. Chegaar, “Investigation of Wind Characteristics in the Southern Region of Algeria”, Energy Procedia, vol. 36, pp. 707–713, 2013.
1. Magister en Ciencias Estadísticas, Docente Facultad de Ingeniería de la Universidad del Atlántico. robertoherrera@mail.uniatlantico.edu.co
2. Estudiante de Ingeniería Industrial, Universidad del Atlántico. kpalomino@mail.uniatlantico.edu.co
3. Estudiante de Ingeniería Industrial, Universidad del Atlántico. fabireyesjimez@gmail.com
4. Magister en Ingeniería Mecánica, Docente Facultad de Ingeniería de la Universidad del Atlántico. guillermoevalencia@mail.uniatlantico.edu.co