ISSN 0798 1015

Vol. 39 (Number 16) Year 2018 • Page 3

A framework for PEST analysis based on fuzzy decision maps

Marco de trabajo para realizar el análisis PEST basado en mapas de decisión difusos

Maikel LEYVA VÁZQUEZ 1; Jesús HECHAVARRÍA HERNÁNDEZ 2; Noel BATISTA HERNÁNDEZ 3; José Abel ALARCÓN SALVATIERRA 4; Oiner GÓMEZ BARYOLO 5

Received: 11/12/2017 • Approved: 10/01/2018

Content

1. Introduction

2. Methodology

3. Case study

4. Conclusions

Bibliographic references

1. Introduction

PEST (Political, Economic, Social and Technological) framework, is used to assess these four external factors in relation to business situation (Healey, 1994). When environment and legal factors are included it is named PESTEL (Political, Economic, Socio-cultural, Technological, Environment and Legal) analysis (Yüksel, 2012).

The conceptual structure and nature of PEST (Political, Economic, Socio-cultural, and Technological) requires an integrated approach for considering importance and interrelation.  Standard technical framework of PEST does not adequately support that approach providing mainly only a general idea about the macro environmental conditions and situation of a company. Consequently PEST analysis lacks a quantitative approach to the measurement of interrelation among its factors (Yüksel, 2012).

In this paper a new model PEST analysis based fuzzy decision maps (FDM)(Yu & Tzeng, 2006) is presented giving methodological support and the possibility of dealing with interdependence, and feedback . This work is structured as follows: Section 1.1 and 1.2 reviews some important concepts about PEST analysis framework and fuzzy cognitive maps(FCM), respectively. In Section 2, a framework for PEST analysis based on FDM composed of five activities, identifying PEST factors and sub-factors, compare importance, modelling influence, obtaining the steady-state matrix and derive the global weight vector is presented. Section 3 shows a case study of the proposed model applied to vertical farming project environment analysis. The paper ends with conclusions and further work recommendations.

1.1 PEST Analysis

PEST (Political, Economic, Social and Technological), analysis is a precondition analysis with the mains function of the identification of the environment within which the company or project operates and providing data and information that will enable the organization to make predictions about new situations and circumstances (Frynas & Mellahi, 2015; Thompson & Martin, 2010). PEST analysis in the original formulation lack a quantitative approach for measurement. Factors analyzed are generally measured and evaluated independently (Yüksel, 2012).

PEST have a hierarchical structure of objective, factor and sub-factor. In (Yüksel, 2012) a proposal for PEST analysis in a multicriteria environment is presented , but only interdependency among general factor is taken into account. Additionally, factors and sub-factor have ambiguity, vagueness in their interrelations.

This study presents a model to address problems encountered in the measurement and evaluation process of PEST analysis considering interdependencies among sub-factors. The integrated structure of PEST sub-factors was modeled by FCM and a quantitative analysis is developed based on the FDM method.

1.2 Fuzzy cognitive maps and Fuzzy decision maps

Cognitive maps were introduced by Axelrod (Axelrod, 2015) where nodes represent concept or variables in a domain and arcs indicate positive or negative causal relations. Fuzzy cognitive maps (FCM)(Kosko, 1986) (Figure 1) are fuzzy graph structures for representing causal knowledge, extending cognitive maps with fuzzy values in the  [-1,1] interval to indicate the strength of causal relations.

The matrix representation of FCM allows to make causal inferences. In FCM there are three possible types of causal relations between nodes represented in the matrix: negative, positive and no relationship (M. Leyva-Vázquez, Santos-Baquerizo, Peña-González, Cevallos-Torres, & Guijarro-Rodríguez, 2016).

Figure 1
Example of FCM graphical representation

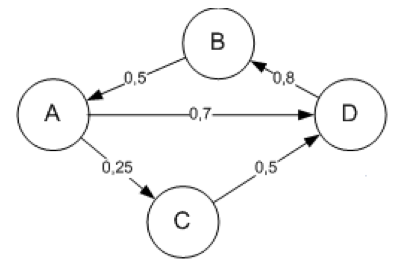
(Maikel Leyva-Vázquez, Karina Pérez-Teruel, Ailyn Febles-Estrada, & Jorge Gulín-González, 2013).

FCM have been applied diverse areas specially decision support and complex systems analysis (MY Leyva-Vázquez, KY PÉREZ-TERUEL, Ailyn Febles-Estrada, & Jorge Gulín-González, 2013).  Fuzzy decision map (FDM) were proposed in 2006 for solving the multicriteria decision making problem with dependence and feedback (Yu & Tzeng, 2006). For  overcoming the shortcoming of AHP and ANP method it incorporates the eigenvalue method, FCM, and the weighting equation (Elomda, Hefny, & Hassan, 2013).

The advantages of FDM (Elomda et al., 2013; Tzeng, Chen, Yu, & Shih, 2010) are overcoming the drawbacks of the AHP and ANP, employing the different threshold functions to indicate the various kinds of relationship among criteria, dealing with direct and indirect influences. The ability to solve both the compound and the interaction effects is another area of advantage.

Our aim in the proposal is developing a framework for PEST analysis based on FDM. The model consists of the following phases (graphically, Figure 2).

Figure 2
Proposed framework for PEST analysis

2.1 Identifying PEST factors and sub-factors

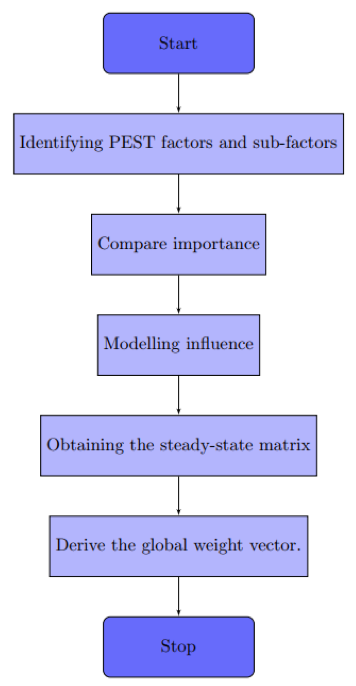
In this step, the relevant PEST factors and sub-factors are identified. PEST factors are derived from the themes: political, economic, socio-cultural, technological factors. Identifying PEST factors and sub-factors allowing to form a hierarchical structure of the model.

2.2 Compare importance

Compare the importance among criteria to derive the local weight vector using the eigenvalue approach (Elomda et al., 2013). This should be done by domain experts according to the preference scale shown below.

Table 1
Scale for realshionship among criteria

2.3 Modelling influence

Depict the fuzzy cognitive map to indicate the influence among criteria by the expert. Causal interdependencies among PEST sub-factors are modelled. This step consists of the formation of FCM of sub-factors, as nodes according to the views of the expert team.

2.4 Obtaining the steady-state matrix

Calculate the updating equation to obtain the steady-state matrix:

2.5 Derive the global weight vector

 We should first normalize the local weight vector () and the steady-state matrix (M) as follows:

Environmental concerns, including issues of ecological justice, attention to sustainability, and focus on issues of food security have gathered increased momentum in vertical farming (Besthorn, 2013). This case study is based in a vertical farming project proposal at the University of Guayaquil. In recent years, Guayaquil has become a city of cement with scarcity on green areas (Delgado, 2013).

The main goal of the project is the optimization and use of spaces not suitable for cultivation, such as walls and terraces; with systems of supports helping in the beautification of the environment and allow the planting distinct types of plants obtaining a commercial harmony sustained in the environment.

Initially factors and sub-factors were identified. Figure 3 shows the hierarchical structure.

Figure 3
The hierarchical model of PEST in the vertical farming project.

For choosing the best alternative, we should derive the influence scores of each criterion and calculate the influence scores of each factor. 

The Scoring matrix (E) was elicited as follows:

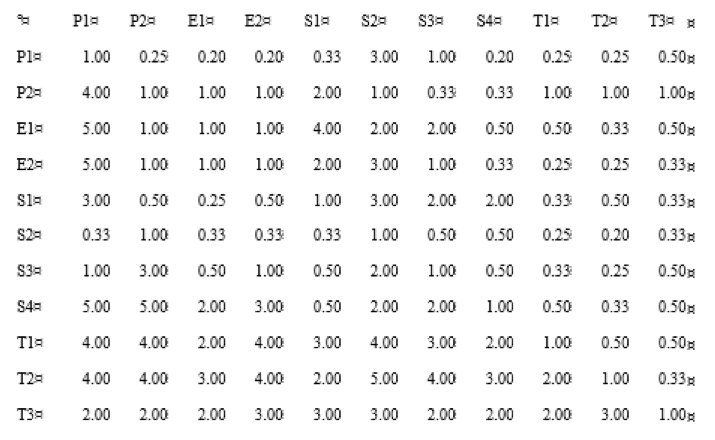
From the matrix above, we can calculate the local weights by means of the eigenvalue method (Table 2).

Table 2
Local Weights

Interdependencies are identified and modelled by means of a FCM. using the Mental Modeler Tool(Gray, Gray, Cox, & Henly-Shepard, 2013).

Figure 4
Fuzzy Cognitive Map

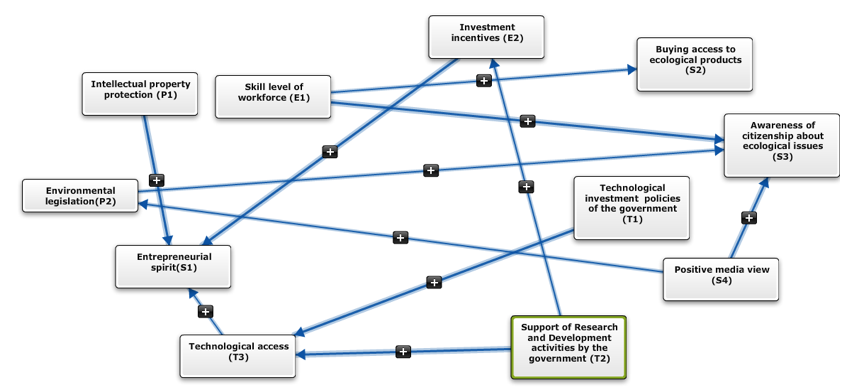
Adjacency matrix of the FCM, which contained all of the weights of the connections is as follows:

Next, by using the pure-linear, we can calculate the steady-state matrices. Finally, using Eq. (3), we can obtain the global weights as shown in Table 3.

 Table 3
global weights

Calculations were made using the IPython kernel for Jupyter Notebook interface (Ragan-Kelley et al., 2014).

Figure 5
Jupyter Notebook interface

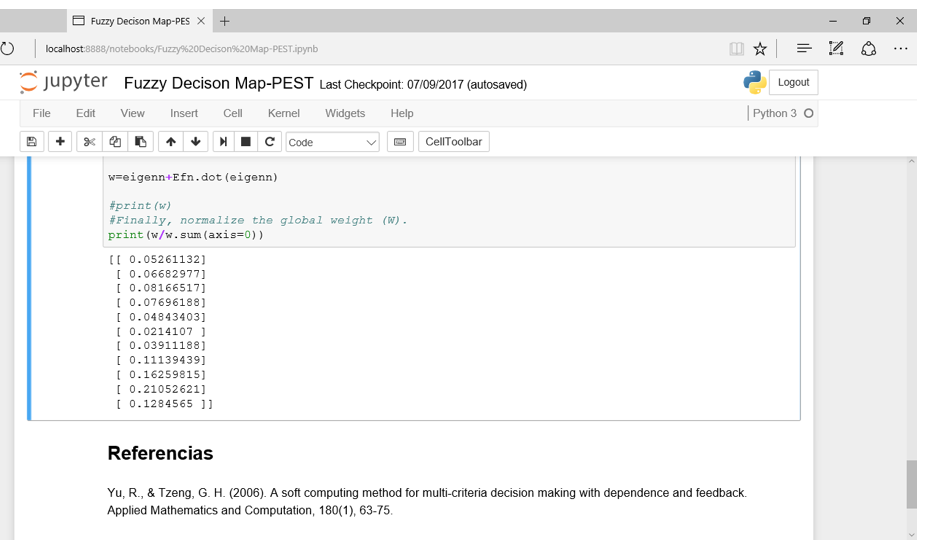
The ranking obtained is as follows:

Support of research and development activities by the government was selected as the top environment factor at this vertical farming initiative. After application in this case study the model is found to be practical to use. The FDM gives a high flexibility and consider interdependencies within PEST analysis.

This study presents a model to address problems encountered in the measurement and evaluation process of PEST analysis considering interdependencies among sub-factors and modeling uncertainty. The integrated structure of PEST sub-factors was modeled by FCM.

To demonstrate the applicability of the proposal a case study to a vertical farming project proposed at the University of Guayaquil.  Most notably, this is the first study to our knowledge to integrate FDM to the PEST analysis Schema. Our approach has many applications in complex decision problem that include interdependencies among criteria, and such as complex agriculture decision support.

Further works will concentrate in extending the model for dealing scenario analysis and the use of compensatory operator in static analysis (M. Y. Leyva-Vázquez, Bello-Lara, & Espín-Andrade, 2014) . Another area of future work is the developing a consensus model for FCM and the development of a software tool.

Axelrod, R. (2015). Structure of decision: The cognitive maps of political elites: Princeton university press.

Besthorn, F. H. (2013). Vertical farming: Social work and sustainable urban agriculture in an age of global food crises. Australian Social Work, 66(2), 187-203.

Delgado, A. (2013). Guayaquil. Cities, 31, 515-532. doi:https://doi.org/10.1016/j.cities.2011.11.001

Elomda, B. M., Hefny, H. A., & Hassan, H. A. (2013). An extension of fuzzy decision maps for multi-criteria decision-making. Egyptian Informatics Journal, 14(2), 147-155. doi:http://dx.doi.org/10.1016/j.eij.2013.05.001

Frynas, J. G., & Mellahi, K. (2015). Global strategic management: Oxford University Press, USA.

Gray, S. A., Gray, S., Cox, L. J., & Henly-Shepard, S. (2013). Mental modeler: a fuzzy-logic cognitive mapping modeling tool for adaptive environmental management. Paper presented at the System Sciences (HICSS), 2013 46th Hawaii International Conference on.

Healey, N. M. (1994). The transition economic of central and eastern Europe: A political, economic, social and technological analysis. The Columbia Journal of World Business, 29(1), 62-70.

Kosko, B. (1986). Fuzzy cognitive maps. International Journal of man-machine studies, 24(1), 65-75.

Leyva-Vázquez, M., PÉREZ-TERUEL, K., Febles-Estrada, A., & Gulín-González, J. (2013). Modelo para el análisis de escenarios basados en mapas cognitivos difusos: estudio de caso en software biomédico. Ingenieria y Universidad, 17(2), 375-390.

Leyva-Vázquez, M., Pérez-Teruel, K., Febles-Estrada, A., & Gulín-González, J. (2013). Técnicas para la representación del conocimiento causal: un estudio de caso en Informática Médica. Revista Cubana de información en ciencias de la salud, 24(1), 73-83.

Leyva-Vázquez, M., Santos-Baquerizo, E., Peña-González, M., Cevallos-Torres, L., & Guijarro-Rodríguez, A. (2016). The Extended Hierarchical Linguistic Model in Fuzzy Cognitive Maps. Paper presented at the Technologies and Innovation: Second International Conference, CITI 2016, Guayaquil, Ecuador, November 23-25, 2016, Proceedings 2.

Leyva-Vázquez, M. Y., Bello-Lara, R., & Espín-Andrade, R. A. (2014). Compensatory fuzzy logic for intelligent social network analysis. Revista Cubana de Ciencias Informáticas, 8(4), 74-85.

Ragan-Kelley, M., Perez, F., Granger, B., Kluyver, T., Ivanov, P., Frederic, J., & Bussonnier, M. (2014). The Jupyter/IPython architecture: a unified view of computational research, from interactive exploration to communication and publication. Paper presented at the AGU Fall Meeting Abstracts.

Thompson, J. L., & Martin, F. (2010). Strategic management: awareness & change: Cengage Learning EMEA.

Tzeng, G.-H., Chen, W.-H., Yu, R., & Shih, M.-L. (2010). Fuzzy decision maps: a generalization of the DEMATEL methods. Soft Computing, 14(11), 1141-1150. doi:10.1007/s00500-009-0507-0

Yu, R., & Tzeng, G.-H. (2006). A soft computing method for multi-criteria decision making with dependence and feedback. Applied Mathematics and Computation, 180(1), 63-75.

Yüksel, I. (2012). Developing a multi-criteria decision making model for PESTEL analysis. International Journal of Business and Management, 7(24), 52-66.

1. PhD. En Ciencias Técnicas, , MSc. En Bioinformática, Facultad de Ciencias Matemáticas y Físicas, Universidad de Guayaquil, Guayaquil Ecuador. mleyvaz@gmail.com

2. PhD. En Ciencias Técnicas, MSc en Diseño y Fabricación Asistida por Computadoras CAD/CAMFacultad de Arquitectura y Urbanismo,  Universidad de Guayaquil, Guayaquil Ecuador. jesus.hechavarriah@ug.edu.ec

3. MSc. en Administración Pública. Facultad de Jurisprudencia y Ciencias Sociales. Universidad de Guayaquil, Guayaquil Ecuador. noelbatista1965@gmail.com

4. MSc. en Sistemas de Información Gerencial, Facultad de Ciencias Matemáticas y Físicas. Universidad de Guayaquil, Guayaquil Ecuador. abel.alarcons@ug.edu.ec

5. PhD. En Ciencias Técnicas, Facultad de Sistemas Computacionales y Telecomunicaciones de la Universidad Tecnológica ECOTEC, Samborondón, Guayas, Ecuador. ogomez@ecotec.edu.ec