ISSN 0798 1015

Vol. 39 (Nº 15) Año 2018. Pág. 22

Mapas cognitivos borrosos para el análisis de modelos mentales

Fuzzy Cognitive Maps for the analysis of mental models

Glenda VERA-MORA 1; Maikel LEYVA-VÁSQUEZ 2; Joffre LEÓN-ACURIO 3; Miguel BOTTO-TOBAR 4

Recibido: 26/01/2018 • Aprobado: 26/02/2018

Contenido

1. Introducción

2. Desarrollo

3. Materiales y métodos

4. Estudio de caso

5. Conclusiones

Referencias Bibliográficas

1. Introducción

Los modelos mentales son representaciones internas de una realidad externa de cada individuo. Esto, quiere decir, que, de la misma realidad externa, cada individuo puede tener variadas representaciones internas. Estas representaciones son modeladas frecuentemente mediante representaciones causales (Pérez Teruel, Vázquez, Yelandi, & Estrada Sentí, 2014).

Los modelos causales son herramientas empleadas frecuentemente, para la comprensión y análisis de  los sistemas complejos (Glykas, 2010; Sharif & Irani, 2006). Para considerar la causalidad desde un punto de vista computacional, se requiere la obtención de modelos causales imprecisos que tomen en consideración la incertidumbre (Puente Agueda, 2011). El razonamiento causal es útil en la toma de decisiones por dos razones fundamentales: primero, es natural y fácil de entender; segundo, es convincente porque explica el por qué se llega a una conclusión particular.

Una concepción general sobre el aprendizaje representa una herramienta heurística indispensable, para el trabajo diario de los docentes; les brinda una comprensión de los complejos y diversos fenómenos que tienen lugar en el aula, y por lo tanto, un fundamento teórico, metodológico y práctico para planificar, organizar, dirigir, desarrollar y evaluar su práctica profesional, perfeccionándola continuamente. Todo ello, constituye un requisito básico con la finalidad que el docente pueda potenciar, de manera científica e intencional -y no empírica o intuitivamente- los tipos de aprendizajes necesarios, es decir, aquellos que propician en sus estudiantes el crecimiento y enriquecimiento integral de sus recursos como seres humanos, en otras palabras, los aprendizajes desarrolladores (Castellanos, Castellanos, Llivina, & Silverio, 2001; Fernández et al., 2017) resultando importante los cambios en los modelos mentales de los estudiantes

Los Mapas Cognitivos Borrosos (MCB)  (Figura 1.), son una técnica creada  por Kosko (J. L. Salmeron, 2009) como una extensión de los mapas cognitivos, utilizando lógica borrosa (B. Kosko, 1986). El objetivo del trabajo es desarrollar un procedimiento, para la representación de modelos mentales, ilustrando las ventajas de los MCB, en la representación de la causalidad, a través de un estudio de casos en la contribución del proceso docente educativo.

El artículo continúa con una revisión de los conceptos fundamentales implicados en el trabajo. Posteriormente se describe un procedimiento para la determinación de relaciones causales entre las variables de interés en modelos mentales. Se desarrolla un estudio de caso que refleja la aplicabilidad de propuesta y muestra una situación práctica en la representación de la relación entre las competencias de la carrera de Ingeniería en Sistemas. El trabajo finaliza con las conclusiones y recomendaciones de trabajos futuros.

2. Desarrollo

La causalidad involucra una transferencia de cualidades desde la causa hasta el efecto, denotado por una flecha dirigida (Sobrino, Puente, & Olivas, 2017). Cada modelo causal puede ser representado por un grafo dirigido , denominado grafo causal (Sobrino, 2012). Existen diferentes formas de causalidad que pueden ser expresados de forma gráfica.

El modelado causal resulta importante para entender el proceso de toma de decisiones (Hagmayer & Sloman, 2005), sin embargo, dada su utilidad y múltiples aplicaciones prácticas, es un área que se debe continuar su estudio. La causalidad se ve generalmente como una relación precisa: la misma causa, provoca siempre el mismo efecto. Pero, en el mundo cotidiano, los enlaces entre causa y efecto son frecuentemente imprecisos o imperfectos por naturaleza (Puente Águeda, Olivas Varela, & Sobrino Cerdeiriña, 2010).

Para considerar la causalidad se requiere la obtención de modelos causales imprecisos. Por esto, es necesario la utilización de técnicas de Soft Computing (Puente Agueda, 2011),  dentro de estas tenemos las redes bayesianas (RB)  y los MCB.

Las técnicas de las RB permiten seleccionar solo las variables que tienen relaciones causales, para el cálculo de las probabilidades condicionadas, la cual se define como la ocurrencia de un suceso dado que otro ha ocurrido anteriormente. Una RB muestra la estructura relación-dependencia entre las diferentes variables del dominio (nodos) y su distribución de probabilidad. Estas redes ofrecen un modelo apropiado que caracteriza la causalidad en términos de probabilidades condicionales, los cuales, han tenido importante aplicabilidad. (4,7.8) (Sobrino, 2012). En este sentido, han sido ampliamente utilizadas (Pearl, 2000; Williamson, 2005) .

Sin embargo, estos modelos presentan limitaciones en el manejo de la existencia de ciclos en las relaciones causales (Zhi-Qiang, 2001) . Otra limitación, está dada por la dificultad que se tiene para determinar de manera exacta las probabilidades (Sobrino, 2012) ; y la falta de usabilidad de la técnica en la interacción con humanos.

En la práctica es necesario representar el grado de influencia entre conceptos y/o resulta difícil encontrar una relación probabilística. Ante estas circunstancias la lógica borrosa resulta una alternativa para representar la causalidad en presencia de vaguedad mediante grafos borrosos.

La teoría de los conjuntos borrosos o borrosos fue introducida por (Zadeh, 1965) en el año 1965. La lógica borrosa ofrece un marco adecuado en el tratamiento de la causalidad imperfecta, haciendo uso de la vaguedad. Para expresar el grado de causalidad entre conceptos se pueden emplear expresiones lingüísticas como "negativamente fuerte", "positivamente fuerte", "negativamente débil", "positivamente débil", etc.(Sokar, Jamaluddin, Abdullah, & Khalifa, 2011).

Los conjuntos borroso son mejores en la captura de  relaciones en que existas distintos grados de pertenecía tales como las de  amigo de (Wierman, 2010) . Una relación borrosa en X es un mapeo R∶ X × X → [ 0 ,1 ], donde R ( x ,y) indica el grado de relación de x con y (Yager, 2010) . Esto permite la ampliación del concepto de las conexiones en una red al poderse referir no solo a si dos nodos están conectados o no, sino las conexiones borrosas nos permiten ver qué tanto están conectados los nodos. Se denota un grafo difuso como G = <V,E,R>  siendo V el conjunto de vértices, E es el conjunto de aristas y R es una relación R∶ V × V → [ 0,1].

2.1. MCB como representación de modelos mentales

Los MCB mejoran los mapas cognitivos, describiendo la fortaleza de la relación mediante el empleo de valores borrosos en el intervalo [-1,1] o más recientemente computación con palabras (CWW)  (Rickard, Aisbett, & Yager, 2015); y es especial, el modelo de 2-tuplas. La CWW es una metodología que permite realizar un proceso de computación y razonamiento, utilizando palabras pertenecientes a un lenguaje en lugar de números. Dicha metodología permite crear y enriquecer modelos de decisión, en los cuales, la información vaga e imprecisa es representada a través de variables lingüísticas.

Un MCB se puede representar a través de un grafo dirigido ponderado donde los nodos representan conceptos y los arcos indican una relación causal (B. Kosko, 1997). Una matriz de adyacencia es construida a partir de los valores asignados a los arcos generalmente de forma numérica (Zhi-Qiang, 2001).

En los MCB existen tres posibles tipos de relaciones causales entre conceptos:

• Causalidad positiva ( > 0): Indica una causalidad positiva entre los conceptos  y , es decir, el incremento (disminución) en el valor de  lleva al incremento (disminución) en el valor de .
• Causalidad negativa (< 0): Indica una causalidad negativa entre los conceptos  y , es decir, el incremento (disminución) en el valor de  lleva la disminución (incremento) en el valor de .
• No existencia de relaciones ( = 0): Indica la no existencia de relación causal entre  y .

Dada la gran utilidad de los MCB, estos han sido extendidos para modelar diversas situaciones. Así, encontramos extensiones basadas la teoría de los sistemas grises (Salmeron, 2010), intervalos (Papageorgiou, Stylios, & Groumpos, 2006), lógica difusa intuicionista (Iakovidis & Papageorgiou, 2011), entre otras extensiones.

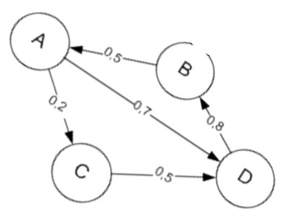
Un MCB puede ser representado a través de un dígrafo (Figura 1.) , en el cual, los nodos representan conceptos y los arcos indican relación causal (B. Kosko, 1997).

Figura 1
Mapa cognitivo difuso (Elaboración propia)

Cuando participa un conjunto de individuos (k), la matriz de adyacencia se formula a través de un operador de agregación, como por ejemplo la media aritmética. El método más simple consiste en encontrar la media aritmética de cada una de las conexiones para cada experto. Para k expertos, la matriz de adyacencia del MCB final (E) es obtenida como (Bart Kosko, 1988):

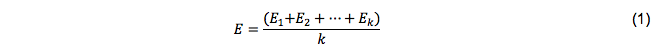
Esta facilidad de agregación permite la creación de modelos mentales colectivos con relativa facilidad.

Los MCB proveen esquemas más realistas, para la representación del conocimiento con respecto a las RB (Glykas, 2010; Lin & Lee, 2002; Mazlack, 2009). Entre los elementos que permiten una representación más realista del conocimiento se encuentra la posibilidad de representar ciclos, la vaguedad y la ambigüedad, presentan; además, una mayor usabilidad para obtener conocimiento de los expertos (Ping, 2009). Otra ventaja está dada en la posibilidad de utilizar el concepto de variable lingüística aumentando capacidad en la interpretación de estos modelos. Los modelos mentales obtenidos son más cercanos al modo de pensar de los estudiantes, permitiendo influir en el cambio los mentales en los participantes y el logro de consenso de los involucrados (Scott, Cavana, & Cameron, 2016).

3. Materiales y métodos

La realización del estudio se desarrolló a través de un procedimiento para la obtención de modelos mentales los MCB como técnica de representación de este conocimiento. Donde su representación gráfica se puede apreciar en la Figura 2.

Figura 2
Modelo propuesto (Elaboración propia)

Actividades correspondientes a los procesos:

1. Seleccionar variables: En esta actividad se seleccionan las variables que se desean incluir; para ello, se recomienda realizar consulta de expertos. Los expertos pueden ser seleccionados utilizando el método de coeficiente de competencias. Posteriormente se determinan los nodos que están representados por los conceptos.
2. Determinar las relaciones causales: Se determinan las relaciones causales existentes entre los conceptos. En esta actividad, los estudiantes son consultados para determinar las relaciones causales existentes entre ellos. Se obtiene finalmente un valor difuso en el intervalo [-1,1]
3. Obtener  modelo mental: Existen distintas propuestas para la obtención de modelos mentales en forma de MCB (Ping, 2009; Jose L. Salmeron, 2009). En el caso de los mapas cognitivos borrosos se sigue la propuesta de Leyva-Vázquez y colaboradores (M.Y. Leyva-Vázquez, Rosado-Rosello, & Febles-Estrada, 2012).
4. Analizar modelo mental: En los modelos mentales difusos resulta importante analizar las características estáticas del modelo (Maikel Y Leyva-Vázquez, Bello-Lara, & Espín-Andrade, 2014).El análisis estático puede contribuir a determinar en qué aspectos del sistema incidir o en reducir la cantidad de criterios que se analizan.

En esta actividad se ordenan los nodos de acuerdo con su importancia en el modelo de tomando en consideración al valor obtenido a partir de la(s) medida(s) seleccionada(s). Adicionalmente se puede emplear sus resultados para visualizar el grafo difuso posibilitando un mejor análisis.

La medida de centralidad empleada es la centralidad de grado (), se calcula a partir de la suma de su grado de entrada () y grado de salida (), tal como se expresa en la fórmula siguiente:

El modelo propuesto, puede ser empleado en disímiles situaciones prácticas, que conllevan la obtención y análisis de modelos mentales de los estudiantes.

4. Estudio de caso

La ingeniería en sistemas(Pollo Cattaneo et al., 2016) es una rama de la ingeniería que se encarga de diseñar, programar, aplicar y mantener sistemas informáticos. Un concepto claro y conciso de competencia es “Posee competencia profesional quien dispone de los conocimientos, destrezas y actitudes necesarias, para ejercer una profesión, resolver problemas profesionales de forma autónoma y flexible y está capacitado, para colaborar en su entorno profesional y en la organización del trabajo” (Bunk, 1994). Es necesario, identificar las competencias en el ámbito laboral, con la finalidad que el ingeniero pueda desenvolverse adecuadamente y ser capaz de resolver situaciones complejas.

En el estudio, se representa la relación entre las competencias; en este caso, un subconjunto de las llamadas competencias transversales (Tabla 1).

Tabla 1
Competencias analizadas

Fuente: Elaboración propia

A continuación (Tabla 2) se muestra el conjunto de etiquetas lingüísticas empleadas.          

Tabla 2
Términos lingüísticos empleados

Fuente: Elaboración propia

Este conjunto de términos lingüísticos para representar las relaciones causales se muestra en la Figura 2.

Figura 2
Conjunto de etiquetas lingüísticas (elaboración propia)

Se obtuvo el modelo mental y se realizó el análisis empleado la herramienta Mental Modeler (Gray, Gray, Cox, & Henly-Shepard, 2013).

Figura 3
Modelo mental obtenido

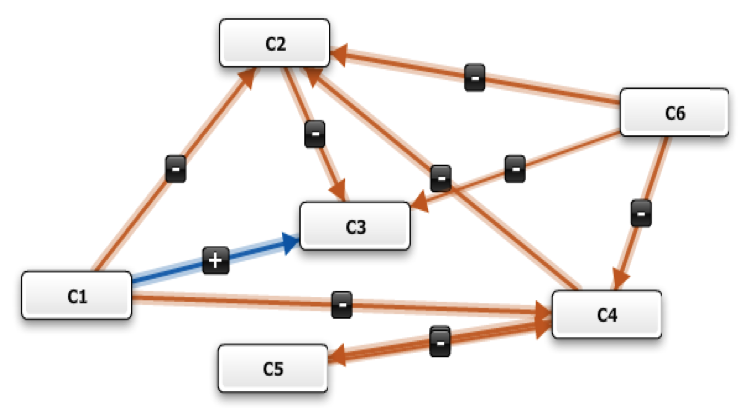
Fuente: (Pérez-Teruel, Leyva-Vázquez, Espinilla, & Estrada-Sentí, 2014)

A continuación, se muestra en la Tabla 3, la matriz de adyacencia obtenida.

Tabla 3
Matriz de adyacencia

Fuente: Elaboración propia

A continuación, se muestran los resultados y principales medidas obtenidas en el análisis estático.

Tabla 4
Resultados del análisis estático

Fuente: Elaboración propia

Como resultado del análisis se determina el siguiente orden de importancia para las competencias analizadas de acuerdo con la centralidad.

En este estudiante las competencias más importantes resultan la comprensión y dominio de los conceptos básicos sobre las leyes de la informática y la capacidad para resolver problemas dentro de su área de estudio.

En el presente estudio, se evidencia como los MCB constituyen una técnica eficiente en la representación de los modelos mentales. Una de las ventajas que presentan los modelos obtenidos con esta técnica, reconocida por los expertos, es la facilidad para ser interpretada, lo que posibilita que los estudiantes puedan interpretar y socializar los modelos causales obtenidos sin dificultad.

5. Conclusiones

Los modelos mentales son representaciones internas la realidad externa de cada estudiante. Esto significa que, de la misma realidad externa, cada individuo puede tener variadas representaciones internas. Estos modelos mentales requieren visualización y análisis para determinar cuáles son los elementos fundamentales.

En este trabajo se mostró el modelo de relación en las competencias, ilustrando las ventajas de los MCB en la representación de modelos mentales, a través de un estudio de casos, para la contribución al proceso docente educativo. Las competencias más importantes resultan la comprensión y dominio de los conceptos básicos sobre las leyes de la informática y la capacidad para resolver problemas dentro de su área de estudio de la ingeniería en sistemas.

Se presentó, además, un procedimiento para la obtención de modelos mentales. La aplicación a nuevas áreas de la pedagogía y el empleo de métricas de redes complejas que contribuyan a evaluar el conocimiento sistémico de los estudiantes es otra de las futuras áreas de trabajo. Se desarrollarán adicionalmente medidas de consenso que permitan analizar las divergencias en la percepción de sistemas complejos por los distintos actores y se incluirá el análisis dinámico.

Referencias Bibliográficas

Bunk, G. (1994). La transmisión de las competencias en la formación y perfeccionamiento profesionales de la RFA. Revista europea de formación profesional(1), 8-14.

Castellanos, D., Castellanos, B., Llivina, M., & Silverio, M. (2001). Hacia una concepción del aprendizaje desarrollador. Instituto Superior Pedagógico “Enrique José Varona”. Colección Proyectos. La Habana.

Fernández, R. L., Rodríguez, R. C., Urquiza, D. E. P., González, L. L., Saltos, M. B. G., & Gálvez, S. S. (2017). La inclusión educativa en la educación a distancia mediante plataformas gestoras. Medisur, 15(2).

Glykas, M. (2010). Fuzzy Cognitive Maps: Advances in Theory, Methodologies, Tools and Applications: Springer Verlag.

Gray, S. A., Gray, S., Cox, L. J., & Henly-Shepard, S. (2013). Mental modeler: a fuzzy-logic cognitive mapping modeling tool for adaptive environmental management. Paper presented at the System Sciences (HICSS), 2013 46th Hawaii International Conference on.

Hagmayer, Y., & Sloman, S. A. (2005). Causal models of decision making: choice as intervention.

Iakovidis, D. K., & Papageorgiou, E. (2011). Intuitionistic Fuzzy Cognitive Maps for Medical Decision Making. Information Technology in Biomedicine, IEEE Transactions on, 15(1), 100-107. doi:10.1109/titb.2010.2093603

Kosko, B. (1986). Fuzzy cognitive maps. International Journal of Man-Machine Studies, 24(1), 65-75.

Kosko, B. (1988). Hidden patterns in combined and adaptive knowledge networks. International Journal of Approximate Reasoning, 2(4), 377-393.

Kosko, B. (1997). Fuzzy engineering: Prentice-Hall, Inc.

Leyva-Vázquez, M. Y., Bello-Lara, R., & Espín-Andrade, R. A. (2014). Compensatory fuzzy logic for intelligent social network analysis. Revista Cubana de Ciencias Informáticas, 8(4), 74-85.

Leyva-Vázquez, M. Y., Rosado-Rosello, R., & Febles-Estrada, A. (2012). Modelado y análisis de los factores críticos de éxito de los proyectos de software mediante mapas cognitivos difusos. Ciencias de la Información, 43(2), 41-46.

Lin, C. T., & Lee, C. S. G. (2002). Neural-network-based fuzzy logic control and decision system (Vol. 40, pp. 1320-1336): IEEE.

Mazlack, L. J. (2009). Representing Causality Using Fuzzy Cognitive Maps. 1-6.

Papageorgiou, E., Stylios, C., & Groumpos, P. (2006). Introducing Interval Analysis in Fuzzy Cognitive Map Framework Advances in Artificial Intelligence. In G. Antoniou, G. Potamias, C. Spyropoulos, & D. Plexousakis (Eds.), (Vol. 3955, pp. 571-575): Springer Berlin / Heidelberg.

Pearl, J. (2000). Causality: models, reasoning, and inference: Cambridge University Press.

Pérez-Teruel, K., Leyva-Vázquez, M., Espinilla, M., & Estrada-Sentí, V. (2014). Computación con palabras en la toma de decisiones mediante mapas cognitivos difusos. Revista Cubana de Ciencias Informáticas, 8(2), 19-34.

Pérez Teruel, K., Vázquez, L., Yelandi, M., & Estrada Sentí, V. (2014). Proceso de consenso en modelos mentales y aplicación al desarrollo de software ágil en bioinformática. Revista Cubana de Información en Ciencias de la Salud, 25(3), 318-332.

Ping, C. W. (2009). A Methodology for Constructing Causal Knowledge Model from Fuzzy Cognitive Map to Bayesian Belief Network. (PHD), Chonnam National University.  

Pollo Cattaneo, M. F., Pytel, P., Vegega, C., Ramón, H. D., Deroche, A., Straccia, L., . . . Acosta, M. P. (2016). Implementación de sistemas inteligentes para la asistencia a alumnos y docentes de la carrera de Ingeniería en Sistemas de Información. Paper presented at the XVIII Workshop de Investigadores en Ciencias de la Computación (WICC 2016, Entre Ríos, Argentina).

Puente Agueda, C. (2011). Causality in Sciencie. Pensamiento Matemático(1), 12.

Puente Águeda, C., Olivas Varela, J. A., & Sobrino Cerdeiriña, A. (2010). Estudio de las relaciones causales. Anales de mecánica y electricidad,, 87, 54-59.

Rickard, J. T., Aisbett, J., & Yager, R. R. (2015). Computing With Words in fuzzy cognitive maps. Paper presented at the Fuzzy Information Processing Society (NAFIPS) held jointly with 2015 5th World Conference on Soft Computing (WConSC), 2015 Annual Conference of the North American.

Salmeron, J. L. (2009). Augmented fuzzy cognitive maps for modelling LMS critical success factors. Knowledge-Based Systems, 22(4), 275-278.

Salmeron, J. L. (2009). Supporting decision makers with Fuzzy Cognitive Maps (Vol. 52, pp. 53-59): Industrial Research Institute, Inc.

Salmeron, J. L. (2010). Modelling grey uncertainty with Fuzzy Grey Cognitive Maps. Expert Systems with Applications, 37(12), 7581-7588. doi:10.1016/j.eswa.2010.04.085

Scott, R. J., Cavana, R. Y., & Cameron, D. (2016). Mechanisms for understanding mental model change in group model building. Systems Research and Behavioral Science, 33(1), 100-118.

Sharif, A. M., & Irani, Z. (2006). Applying a fuzzy-morphological approach to complexity within management decision making (Vol. 44, pp. 930-961): Emerald Group Publishing Limited.

Sobrino, A. (2012). Imperfect Causality: Combining Experimentation and Theory. In E. Trillas, P. P. Bonissone, L. Magdalena, & J. Kacprzyk (Eds.), (Vol. 271, pp. 371-389): Springer Berlin / Heidelberg.

Sobrino, A., Puente, C., & Olivas, J. Á. (2017). Mining Temporal Causal Relations in Medical Texts. Paper presented at the International Joint Conference SOCO’17-CISIS’17-ICEUTE’17 León, Spain, September 6–8, 2017, Proceeding.

Sokar, I. Y., Jamaluddin, M. Y., Abdullah, M., & Khalifa, Z. A. (2011). KPIs Target Adjustment Based on Trade-off Evaluation Using Fuzzy Cognitive Maps. Australian Journal of Basic and Applied Sciences, 5(12), 2048-2053.

Wierman, M. J. (2010). An Introduction to the Mathematics of Uncertainty: Center for Mathematics of Uncertainty, Inc.

Williamson, J. (2005). Bayesian nets and causality: philosophical and computational foundations: Oxford University Press.

Yager, R. R. (2010). Concept representation and database structures in fuzzy social relational networks. Systems, Man and Cybernetics, Part A: Systems and Humans, IEEE Transactions on, 40(2), 413-419.

Zadeh, L. A. (1965). Fuzzy sets. Information and Control, 8(3), 338-353. doi:10.1016/s0019-9958(65)90241-x

Zhi-Qiang, L. I. U. (2001). Causation, bayesian networks, and cognitive maps. ACTA AUTOMATICA SINICA, 27(4), 552-566.

1. Magíster en Gerencia de Proyectos Educativos y Sociales, Magíster en Educación Informática y Profesora Titular Agregada de la Facultad de Ciencias Jurídicas, Sociales y de la Educación de la Universidad Técnica de Babahoyo, Babahoyo, Los Ríos, Ecuador. gvera@utb.edu.ec

2. Doctor en Ciencias Técnicas, Máster en Bioinformática y Docente de la Facultad de Ciencias Matemáticas y Físicas de la Universidad de Guayaquil, Guayas, Ecuador. mleyvaz@gmail.com

3. Magíster en Informática Empresarial. Especialista en Redes de Comunicación de Datos. Certificación de Auditor Interno Iso 27001 y Profesor Titular Agregado de la Facultad de Administración, Finanzas e Informáticas de la Universidad Técnica de Babahoyo, Babahoyo, Los Ríos. Ecuador. jvleon@utb.edu.ec

4. Máster Universitario en Ingeniería de Software, Métodos Formales y Sistemas de Información - Universidad de Guayaquil, Ecuador; Eindhoven University of Technology, The Netherlands. m.a.botto.tobar@tue.nl