ISSN 0798 1015

Vol. 39 (Number 14) Year 2018 • Page 25

ClusCTA: A Clustering technique based on Centroid Tracking for Data Streams

ClusCTA: Una técnica de clustering basada en rastreo de centroides para streams de datos

Sonia JARAMILLO-VALBUENA 1; Jorge Mario LONDOÑO-PELÁEZ 2; Sergio Augusto CARDONA 3

Received: 25/11/2017 • Approved: 15/01/2018

Content

1. Introduction

2. Related work

3. The centroid tracking approach

4. Implementation and evaluation

5. Conclusions and future work

Bibliographic references

1. Introduction

In recent years, applications that generate data streams have become commonplace.  A data stream is a continuous and changing sequence of data made available over time (Jiawei & Kamber, 2011).  Telecommunication systems, the financial markets, the retail industry, surveillance systems, scientific and engineering experiments, biological applications and social networks are representative examples. Streaming data presents challenges in different levels: querying, scalability, storage, and   mining (Chaudhry, Show, & Abdelguerfi, 2005).

Traditional data mining techniques are suitable for DBMS and data warehouses, but should be modified, or new algorithms have to be devised to work well on data streams. Data stream mining requires that the data analysis is executed in an online manner, which means that each sample is processed on-the-fly without the need for long term sample storage or reprocessing (Oza & Russell). 

Clustering algorithms are the most common unsupervised machine learning technique. Clustering is the task of partitioning a set of objects in subgroups (called clusters), such that objects in the same cluster are similar and objects belonging to different clusters are dissimilar (Ackermann, y otros, 2012).  Clustering approaches have 3 fundamental characteristics: they often need multiple iterations, the number of rounds of execution is defined by the convergence characteristics and, the algorithms commonly work on multidimensional data (Ericson & Pallickara, 2013).

Motivated by the industry’s need to obtain useful knowledge from data streams in real-time, several clustering methods have been proposed. Most of them divide the clustering process in two stages: online and offline. The first one summarizes the data, and the second creates the final clusters (Ghesmoune, Lebbah, & Azzag, 2016). Data stream clustering poses important challenges, among them, it must be done in a short time and using limited memory.  In addition, it should consider the changing nature of data streams and be able to differentiate the occurrence of outliers or noise from actual changes in the target concept (concept drift) to ensure the quality of the obtained clustering. The outliers refer to random deviations or statistical anomalies (Chandola, Banerjee, & Kumar, 2009). The term “concept drift” means that the statistical properties of the target concept change arbitrarily over time (Widmer & Kubat) (Wang, Yu, & Han, Mining Concept-Drifting Data Streams, 2010) (Minku & Yao, 2012), causing the previously constructed model to be inconsistent, hence requiring an update or to be replaced with a new one to prevent accuracy deterioration (Wang, Fan, Yu, & Han, 2003) (Dongre & Malik). Data stream clustering has important applications in areas such as intrusion detection, sensor networks, user behavior analysis, stock market analysis, and smart cities.

In this paper we propose a new clustering technique for data streams, it is referred as ClusCTA (Clustering based on Centroid TrAcking). This approach uses multiple sliding windows, a clustering algorithm in the initialization phase, and a centroid tracking method for maintaining enough knowledge about centroid behavior.  The centroid tracking lets to get an estimate of the positions, velocities and accelerations of centroids for the next point in time. By maintaining an up-to-date centroid movement model, we avoid recomputations of the clustering model. We evaluated the performance of ClusCTA and compared it with ClusTree (Kranen, Assent, Baldauf, & Seidl, 2011), a state of the art, compact, and self-adaptive index structure, which maintains stream summaries and reports novelty, concept drift, and outliers. The evaluation used the same data streams for both techniques, which included noise and concept drift.

The paper is organized as follows. Section 2 presents preliminaries on data stream clustering. Section 3 describes the technique we propose.  Section 4 shows implementation details and model evaluation. The last section provides a summary of the findings in this work.

After a thorough review of the related literature, we found that stream clustering methods can be classified in 3 categories: partitioning stream methods, density-based stream methods and hierarchical stream methods.

2.1. Partitioning stream methods

This kind of algorithms organizes the instances into clusters, which are formed using a distance function. The clusters obtained have a spherical shape (Ghesmoune, Lebbah, & Azzag, 2016).

StreamKM++ (Ackermann, y otros, 2012) is a partitioning algorithm for data Streams, which uses an adaptive approach similar to the K-means++ seeding procedure to get small coresets.  A coreset is a small weighted example set that approximates the original input example set with respect to a particular optimization problem. StreamKM++ uses a new structure called coreset tree to create a coreset. The coreset tree is a  binary tree data structure that stores examples in such a way that it is possible to perform a fast adaptive sampling, in similar way to the k-means++.  K-means++ (Arthur & Vassilvitskii) is an enhanced version of k-means, by augmenting k-means with a very simple, randomized seeding technique (this is a specific way of choosing the centers, instead of choosing arbitrary centers). A coreset tree for a set of samples P is related with a hierarchical divisive clustering for the set. The tree start with a single cluster, which contains the whole set P, and successively split existing clusters into two subclusters with the restriction that the examples in one subcluster are far from samples in the other subcluster. The dividing process stops when the number of clusters corresponds to the needed number of clusters. The coreset tree satisfies 3 properties: 1) each node of the coreset tree is associated with a cluster in the process of hierarchical divisive cluster. 2) The root of the coreset tree is associated with the single cluster (it contains the whole example set) and 3) the nodes related with the 2 subclusters of a cluster C are the child nodes of the node related with C.  StreamKM++ uses the merge-and-reduce technique proposed by Bentley and Saxe (Bentley, L., & Saxe, 1980) to obtain a small weighted point set (a small coreset), on which uses k-means++ algorithm in their offline component to obtain k clusters.  StreamKM++ runs the k-means++ algorithm on the coreset five times independently and selects the clustering that minimizes the total distance to centroids. A limitation of StreamKM++ is related with the use of k-means++. This algorithm does not work properly in the presence of noise and outliers, and is incapable to detect clusters of arbitrary shapes.

Another method of clustering data streams is CluStream (Aggarwal, Han, Wang, & Yu). This approach is based on the concepts of a pyramidal time frame and microclustering. Pyramidal time frame is a technique that stores snapshots at differing levels of granularity depending on the current time. Since it is not possible to store all snapshots, CluStream chooses a time horizon to store microclusters, which ensures that clusters can be approximated.  A micro-cluster (also called cluster feature) is a temporal extension of feature vectors (Zhang, Ramakrishnan, & Livny, 1996) to create and maintain compact representations of the current clustering. That is, a set of statistics which summarize a set of instances. CluStream works in two phases - online and offline phase. The first one places arriving instances in one of the microclusters kept in main memory, or in a new microcluster if required. The microclusters disappear depending on their expiration timestamp or when close microclusters are merged. In the second phase, a weighted k-means is applied to get the final clusters. The macro-clustering process does not directly use the data stream, only the microclusters, for this reason, CluStream is not restricted by one-pass requirements. CluStream treats the microclusters as pseudo-points which are re-clustered in order to determine higher level clusters. This implies that the k-means algorithm is modified as follows:

- At the initialization stage, the seeds are no longer randomly collected, they are sampled with probability proportional to the quantity of instances in a given micro-cluster.

- At the partitioning stage, the distance of a seed from a micro-cluster (or pseudo-point) is equivalent to the distance of the seed from the center of the micro-cluster.

- The new seed for a given partition, is defined at the seed adjustment stage, as the weighted centroid of the micro-clusters in that partition (Aggarwal, Han, Wang, & Yu).

CluStream, by not manipulating boundary points, offers lower clustering quality. Boundary detection allows detecting the boundary instances which are located in the border of the clusters. This kinds of instances have special features. For example, in the case of patients with tumors, this can be used to detect if they develop malignant tumors (Guo, Wang, & Wang, 2016).

In general, partitioning Clustering Algorithms for Data Stream, usually influenced by noise, are highly sensitive to the selection of the k parameter, the clustering quality heavily depends of the initial centroids, and is restricted to finding convex-shaped clusters [6].

Similar to StreamKM++ and CluStream, our solution works in two phases: An online phase and an offline phase. In the online phase, ClusCTA uses polynomial regression as a strategy to keep up-to-date a clustering model. In the offline phase, ClusCTA uses ClusTree (a hierarchical stream clustering, which is described later), on filtered samples to obtain the clusters. The filtering process runs K-means++ to obtain estimates of the clusters radius, which are used for the outliers filter, named MCOD (Tran, Fan, & Shahabi) (Kontaki, Gounaris, Papadopoulos, Tsichlas, & Manolopoulos). ClusCTA differs from earlier approaches in that it offers better quality of clustering.

2.2. Density-based stream methods

Density-based stream algorithms detect high density and low density areas of the data stream points. The first are considered as clusters, and the second as noise. These methods find clusters of arbitrary shapes. This kind of shapes are observed from applications such as weather satellite images, spatial data, geographic information systems, and epidemiology (Sharma, Gupta, & Tiwari, 2016).

An algorithm representative of this underlying clustering method is DenStream (Cao, Ester, Qian, & Zhou). This method introduces the concepts of core micro-cluster (named c-micro-cluster) and outlier micro-cluster (o-micro-cluster). The first, is a mechanism to summarize the clusters with arbitrary shape.  The outlier micro-cluster is a structure to distinguish outliers.  DenStream applies the DBSCAN algorithm to initialize the possible micro-cluster set. A possible micro cluster for instance p is created when, the total weight in this neighborhood is above βµ, where β is a parameter to determine the threshold of outlier  relative to c-micro-clusters (0 <β ≤ 1) and µ is an integer representing the overall weight of data points in a core object. DenStream includes a pruning strategy based on the condition we< βµ , where we is the exact weight of a possible micro-cluster. This allows a limited memory usage and provides guarantee of the precision of micro-clusters (growth of new clusters while promptly getting remove of the outliers). The non-release of the memory (when micro-clusters are deleted or merged), the time-consuming pruning phase for deleting outliers and no addressing the concept drift problem are considered as drawbacks of the DenStream (Amini, Wah, & Saboohi, 2014). 

The main challenge of Density-based stream methods is the process of density estimation, which may be computationally expensive (Aggarwal C. ).

2.3. Hierarchical stream methods

This clustering groups the data into a binary-tree based data structure (or dendrogram) of clusters, which lets to summarize and visualize the data. The applications of this type of grouping come from areas such as biometric identification systems, sensor networks, students' performance evaluation systems, genomics, and zoology (Pirim, Ekciouglu, Perkins, & Yuceer, 2012).

Hierarchical algorithms do not require a user-predefined number of target clusters. Once the tree is constructed, it is possible to choose the quantity of clusters by splitting the dendrogram at different levels, without re-executing the algorithm for the same dataset (Ghesmoune, Lebbah, & Azzag, 2016).  A representative technique for this kind of clustering is ClusTree (Kranen, Assent, Baldauf, & Seidl, 2011). This approach proposed by Kranen et al., is a parameter-free algorithm that incorporates the age of the objects to give more importance to recent data. It also uses micro-clusters, compact representations of the data distribution, to automatically adapt to the speed of the data stream.   ClusTree is a compact and self-adaptive index structure for keeping stream summaries. The Indexing is achieved by using a structure, which extends from the R-tree (Beckmann, Kriegel, Schneider, & Seeger) (Guttman) (Seidl, Assent, Kranen, Krieger, & Herrmann) family.  This tree lets to store and maintain a compact view of the current clustering. An arriving instance is inserted into the corresponding micro-cluster, and probably merged with aggregates of previous instances. The indexation of micro-clusters, a similar concept to the presented in (Zhou, Cao, Qian, & Jin, 2008), allows to incrementally assign objects to the most similar micro-cluster. A micro-cluster CF = (n, LS, SS) maintains the linear sum LS of n objects and their squared sum.  This tuple allows computing the mean and variance of the microcluster and can be incrementally updated.   

To place a new instance, ClusTree descends the hierarchy to reach the leaf micro-cluster closest to the instance. Each entry in the hierarchy describes the cluster features properties of their corresponding sub tree. Local aggregates are added into the tree as temporary entries.  The local aggregate stores the instance temporarily, using the arrival time for computing a buffered local aggregate regularly.

The ClusTree is created and updated in a similar way to any multidimensional index, with the difference that it stores CF’s instead of the minimum bounding rectangles (in addition to the instances).  For insertion, the ClusTree uses the closest mean calculated by Euclidean distance. For the splitting, the entries are combined in two sets such the sum of the intra-group distances is minimal. An insertion in the ClusTree, has a low runtime of O(log2(n)).

ClusTree has a buffer in each cluster feature to store aggregates or instances that do not reach leaf level during insertion. When a leaf node is reached and the insertion of a new instance would generate a split, ClusTree checks whether there is still time left (If there is no time, the closest two entries are joined).

Clustering has to be performed in a single pass over the incoming data and cannot take longer than the average time between any two objects in the stream (Kranen, Assent, Baldauf, & Seidl, 2011). When a leaf node entry is created, it is assigned an id. Concept drift detection is accomplished by tracking micro-clusters, which assign unique ids to every new leaf entry. When entries are combined, this is recorded in a merging list that contains pair of ids.

The clustering resulting from the ClusTree is the group of CFs stored on the leafs.  By taking the means of the CFs, it is possible to apply a density based algorithm such as Density-based spatial clustering of applications with noise (DBSCAN) to detect clusters of arbitrary shape (Ghesmoune, Lebbah, & Azzag, 2016).

The incremental decision tree algorithms produce a single model that represents the entire data stream. In presence of concept drift, the prediction accuracy is affected when it is necessary to classify an instance that has a very different distribution from the historical data (Wang, Yu, & Han, Mining Concept-Drifting Data Streams, 2010).The authors of (Stahl, Gaber, & Salvador, 2012) discuss the how treescannot abstain from a potentially erroneous classification, since they tend to force the classification of every instance.  It has also been pointed out (Wang, Yu, & Han, Mining Concept-Drifting Data Streams, 2010) that considerable changes (as replacing old branches or building alternative sub-branches) severely compromise the efficiency of the algorithm.

In general, in the context of data stream clustering approaches (partitioning stream methods, density-based stream methods or hierarchical stream methods), we highlight some drawbacks. Recent studies weight the importance of determining suitable criteria to identify the cluster validity in data stream clustering (Khalilian & Mustapha, 2010). Another difficulty is to determine parameters such as the correct cluster partitions in stream of data in special when two or more   clusters move  together  and it is necessary to dynamically merge or split (Hasan, 2014) clusters.  Another drawback arises when trying to achieve a balance between concept drift and noise, in this case a penalty term may reduce the accuracy of clustering (Chen & Luo, 2015).

In this section, we introduce a new Clustering technique based on Centroid Tracking for Data Streams. We refer to this method as ClusCTA.

ClusCTA uses multiple sliding windows and centroid tracking for maintaining enough knowledge about centroid behavior.  The centroid tracking lets to get an estimate of the positions, velocities and accelerations of centroids at  time t.   ClusCTA uses a clustering technique to bootstrap the clusters and build a model that tracks the behavior of cluster centroids.

At the beginning, ClusCTA constructs a clustering model by running 5 times the k-Means++ as soon as the arrival window fills for the first time and it keeps the best of the five clustering models. This technique was used in (Arthur & Vassilvitskii) to prevent that a bad choice of random seeds leads to a poor clustering. Then, based on the estimated radius of the obtained clusters, configures MCOD (Tran, Fan, & Shahabi) (Kontaki, Gounaris, Papadopoulos, Tsichlas, & Manolopoulos) to perform an outlier filtering process.

MCOD is an approach based on microclusters that uses a priority queue to store instances. The micro-clusters correspond to regions containing inliers only, which are  composed of no less than   k + 1 data instances. A micro-cluster has a radius of R/2 and, according to the triangular inequality, the distance between every pair of instances inside this is no greater than R. MCOD performs a range query for each new instance with respect to the (fewer) microcluster centers. Then, MCOD examines the PD list for o′s neighbors within distance R/2.  If there are at least k neighbors in PD then a new microcluster is formed with o as the cluster center. Otherwise, o is added to the PD list (which contains the instances does not fall on a microcluster). After processing the sliding window, the instances in PD that have less than k neighbors are reported as outliers. MCOD is already implemented on the Massive On-line Analysis (MOA) framework (Bifet, Holmes, Kirkby, & Pfahringer, 2010).

MCOD requires setting a search radius as parameter per cluster. To calculate this radius, we sort the distances between the instances in a cluster and its centroid and set as radius the distance corresponding to ninth decile. The first centroids calculated are stored at an array of current Centroids. After this, we maintain a sliding window of samples per cluster with a maximum size of n/k. When a new instance arrives, it is processed individually, associated with a cluster (using a Nearest Neighbor Criteria) and recorded in the sliding window of the corresponding cluster. Additionally, we have a motion window per cluster (of size m). In this window we record the arrival time of the new sample and the impact that it has on the movement of its centroid. The data recorded in the centroid motion window is used to get the tracking model.

To conclude the initialization phase, ClusCTA invokes ClusTree on the filtered window and it returns the clustering model of the initial sample window. 

The application of the ClusTree on the filtered data allows obtaining some a set of good quality initial centroids. It is important for ClusCTA to start the centroid tracking process from a good quality initial centroids, even if there is noise in the data stream.

The centroid tracking model is calculated using multivariate polynomial regression to fit points corresponding the centroid movements, this allows to maintain enough knowledge about centroid behavior (Rossi, Allenby, & McCulloch, 2012, p. 32). The centroid movement model can be assimilated to the continuous - time motion of a particle, of which only a few discrete samples are known. A typical model for the particle movement is the second-order Taylor series expansion around time t.  It is possible to obtain from the tracking function, an estimate of the distance from origin, velocity and acceleration of each centroid. In fact, any polynomial is equal to its Taylor series expansion centered at 0.   The multivariate polynomial regression is an empirical algorithm to model systems based on observed data, advisable when the data does not have much noise.

We obtain the coefficients of the polynomial regression by using Eq. 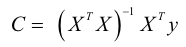(1).

                                                    (1)

X is called the design matrix, in which each row corresponds to a time vector, C is the matrix of coefficients (in this the coefficient vectors   a, b,  c, d… z for each problem i are stacked horizontally) and “y” is a matrix where each row is the estimated centroid at the time instant ti.

The centroid tracking process is repeated for every new instance. A polynomial regression model, is computed for the centroid of each cluster and updated on new instance arrivals. The total time complexity of polynomial regression is O (C2N), where C is total number of features and N are the number of samples (in a sample window, which is a constant). When the model for a cluster is calculated we get a new centroid, which is used to update the array of current Centroids. The clustering resulting from centroid tracking is the set of points stored in this array.  

We implement ClusCTA on top of the Massive On-line Analysis (MOA) framework, a widely known framework for data stream mining written in Java.

After the initialization stage, ClusCTA starts the operation phase.  For this, ClusCTA calculates, with the arrival of a new instance, the impact that it has on the movement of its centroid. This impact is recorded in the clusters centroid motion window. When the centroid motion window is full, it builds the movement model using the  polynomial regression. 

The Centroid Tracking model was implemented using a degree-d polynomial regression. For our experimental evaluation we used d=2. As this is a per-sample process, we used an optimized implementation of Eq. (1) whose performance depends only on the length of the motion window (a constant configurable parameter of the algorithm). The updated centroids are stored in the array of current centroids.

ClusCTA only resets the current centroids when it detects that a centroid is lagging behind the actual cluster. After a reset, the clustering is restarted running again ClusTree.  The centroid lags behind when clusters overlap or when a cluster abruptly changes its speed. In order to detect if a centroid is lagging behind, we use two strategies: A Multivariate Exponentially Weighted Moving Average (MEWMA) filter, and a cluster size estimator. The MEWMA filter (Hotelling, 1931) (Lowry, Woodall, Champ, & Rigdon, 1992) allows computing the Hotelling’s T2 (Lowry, Woodall, Champ, & Rigdon, 1992) control chart (a distance measure) that when above a given threshold gives an out-of-control signal.

The second, considers the number of instances that belong to the cluster (this is, the cluster queue), when it falls below a given threshold (for example, in a 60% of the sample sliding window size), we conclude that cluster moved, but its centroid is lagging behind. The lag of centroids causes the previously constructed model to be inconsistent, requiring a reset of the clustering model to prevent accuracy deterioration [11-12]. In both cases, invocations of the base clustering technique (ClusTree in our implementation) only occurs when the clustering precision declines.

To evaluate the performance of ClusCTA we executed a set of experiments using both: real-world datasets and synthetic datasets. For comparison purposes, we ran ClusTree (Kranen, Assent, Baldauf, & Seidl, 2011) on the same input streams. We choose ClusTree because, to our knowledge, is the best available algorithm that maintains an updated cluster model and reports concept drift, novelty, and outliers (Kranen, Assent, Baldauf, & Seidl, 2011).

Synthetic datasets were created with the class RandomRBFGeneratorEvents (Bifet, Holmes, Kirkby, & Pfahringer, 2010), which is part of MOA. RandomRBFGeneratorEvents is a generator based on the random Radial Basis Function that adds drift to samples in a stream (Bifet, Holmes, Kirkby, & Pfahringer, 2010). The random radial basis function (Bifet, Holmes, Pfahringer, & Gavalda, 2009)   generates a fixed number of random centroids. Each centroid is defined by the initial random position, the class label, its standard deviation, and its weight. RandomRBFGeneratorEvents creates instances by doing a weighted random selection of a centroid, which determines the label. The random radial basis function gives rise to a normally distributed hyper sphere of instances enclosing each centroid.  Drift is added by moving the centroids at different rates.

We modified the class RandomRBFGeneratorEvents, to allow generating instances with different noise levels and velocities.  In the case of noise, we generate for each n samples, a percentage of random samples outside the clusters defined by the generator. For our experiments we used noise levels of: 0%, 5%, 10%, 15%, and 20%.

For the assessments with synthetic datasets, we create 5 clusters, of which 2 have no movement (speedOption=0) and 3 do. During the experiment execution, a moving cluster can change its speed (speedOption may take 3 different values: 0.01/500, 0.001/500 and 0.1/500). Speed is given as distance units in the feature space every 500 samples. 

As real-world datasets we used Skin_NonSkin and Human Activity Recognition (HAR) (Velloso, Bulling, Gellersen, Ugulino, & Fuks, 2013). Skin Segmentation is a dataset with 245057 examples, out of which 50859 is the skin samples and 194198 is non-skin samples. Skin Segmentation has 3 numeric attributes (x1, x2 and x3) and 2 classes (0 and 1).   Skin Segmentation dataset is generated using information from images of various age groups (young, middle, and old), ethnic groups (white, black, and Asian) and genders.  This dataset is useful to support the decision-making of dermatologists. This information (for being a unique characteristic) has applications in areas as identity confirmation, skin tracking and visual information systems (Bhatt, Sharma, Dhall, & Chaudhury, 2009) (Neshat, Sepidname, Eizi, & Amani, 2015).

The HAR dataset is based on the Human activity recognition and has 165507 samples. The experiments were carried out with 4 volunteers (2 men and 2 women, all adults and healthy) and consider 5 activity classes: sitting, standing up, standing, sitting down, walking. Each person wore tri-axial accelerometers on their waist, left thigh, right arm, and right ankle.  Dataset were collected during 8 hours of activity. Each record has 17 numeric attributes  (age, tall, weight, mass, x1, y1, z1, x1, y1, z1, x2, y2, z2, x3, y3, z3) and  the class label.  Datasets as HAR are useful to provide information about patients’ routines to support the development of healthcare applications (Velloso, Bulling, Gellersen, Ugulino, & Fuks, 2013).

ClusCTA is a clustering-based approach that work with continuous data, a requirement met by both, the Skin_NonSkin and the HAR datasets. Although both datasets are tagged we did not use the tags in the experiments as ClusCTA is an unsupervised clustering algorithm.

For the evaluation, we use a sliding window of 350 centroid movements to construct the polynomial regression model.

In our evaluation we also calculated the quality of clustering and made the comparative analysis with respect to ClusTree for different noise levels. The quality metrics used were the Silhouette coefficient and the F-measure.   The quality results obtained on synthetic datasets over time, are summarized in Figures 1-5. It is also important to clarify that the regression coefficients change over time, as well as the positions of the moving centroids, therefore for space considerations we omit this information.

To analyze the results of Figs. 1-5 we consider the quality measures as random variables that change over time. These random variables do not follow a Gaussian distribution, therefore we used a non-parametric alternative test to compare the two collections of measures. Then we register a performance index for both ClusCTA (our algorithm), and the baseline algorithm ClusTree.

Figure 1
Clustering quality of ClusTree and ClusCTA, noise=0%

Source: Own image

-----

Figure 2
Clustering quality of ClusTree and ClusCTA, noise=5%

Source: Own image

-----

Figure 3
Clustering quality of ClusTree and ClusCTA, noise=10%

Source: Own image

-----

Figure 4
Clustering quality of ClusTree and ClusCTA, noise=15%

Source: Own image

-----

Figure 5
Clustering quality of ClusTree and ClusCTA, noise =20%

Source: Own image

For this purpose, we use Mann-Whitney U test (Mann & Whitney, 1947) for evaluating the results obtained for the Silhouette coefficient the F-measure.  We test the hypothesis of equal medians for two independent samples. The same process is repeated for F-measure.  F-measure is the harmonic mean of Recall and Precision (Makhoul, Kubala, Schwartz, & Weischedel, 1999).  The Table I shows the results obtained.

Table 1
Mann-Whitney U Test for different noise levels

Source: Own image

For the base case (no noise present in the dataset), the behavior of both algorithms is similar. In this case, the analysis shows that the null hypothesis is not rejected, meaning there is not a statistical significant difference between the performances of both algorithms. However, as the noise increases, the figures show that ClusTree’s quality suffers severe drops for some time intervals, while ClusCTA maintains good quality metrics. This observation is confirmed by the statistical analysis of Table 1 that shows that the null hypothesis (that the performance is similar) was rejected for all cases with noise level greater or equal to 5%. This lets us conclude that for all experiments with synthetic datasets, the quality of the centroids obtained with ClusCTA is equal to or higher than with the baseline algorithm.

ClusTree shows difficulties when the cluster changes its speed, especially when it becomes higher. In this case, the centroid “remains behind” in the sense that stays far from the true centroid.

Figure 6
Two ClusTree centroids lag behind, after overlapping

Source: Own image

Figure 6 (left) shows two centroids that remain behind their cluster center after an overlapping event when using ClusTree. Also, for the yellow and orange clusters, ClusTree shows a single centroid. For the same data stream, when running ClusCTA, the centroids are rapidly updated after the overlap event, and maintain good correspondence with the clusters, as shown in Fig. 6 (right). The quality measures obtained with the real-world datasets are presented in Figures 7 and 8. 

Figure 7
Clustering quality of ClusTree and ClusCTA
on real-world data set over (Skin_NonSkin)

 Source: Own image

-----

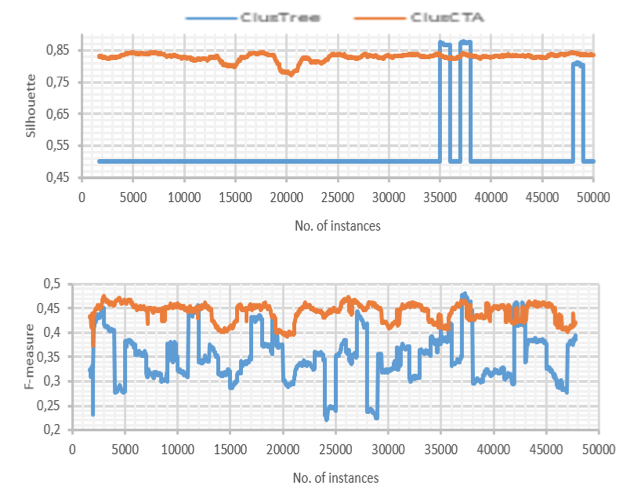
Figure 8
Clustering quality of ClusTree and ClusCTA on real-world data set over HAR

Source: Own image

ClusCTA runs well with both datasets. With ClusCTA, we observe a decrease in F-Measure and Silhouette for HAR dataset, this occurs because the dataset is imbalanced.  The problem of class imbalance consists in almost all the samples are labeled as one class, while far fewer samples are classified as the other class (Guo, Yin, Dong, Yang, & Zhou). ClusCTA scored at or above ClusTree for the Silhouette coefficient and F metrics. Although the results are promising with real-world datasets, they pose significant challenges for learning in unbalanced datasets. It is necessary to improve the recall, which gives the low performance on the F-measure.

In this paper, we propose a new model of clustering online data streams. This new method uses centroid tracking and polynomial regression to predict the centroid movements with high precision, therefore maintaining a very accurate clustering model of streamed data. With ClusCTA the model needs to be recomputed rarely (if at all). It may be noted that other curve-fitting methods could potentially be used. For example, smoothing splines, but exploring this possibility is left for future work.

We showed that our approach provides better or equal quality of clustering compared to ClusTree, a state of the art data stream clustering technique. We observed that, although ClusTree has shorter execution times, with ClusTree it is very possible that the centroids will not correspond to the actual cluster. Hence, the quality of clustering obtained by ClusTree is very poor.  ClusCTA represents a good trade-off between cluster quality and running time. It should also be pointed out that we did a sequential implementation, but there are many parallelizable operations in the algorithm, that would allow significant performance improvements.

Our experiments also showed that the filtering process for discarding noise instances, contributed to the quality of clustering. Quality is also linked to a good starting set of centroids. We used the 5-times k-means++ heuristic to obtain a good set of starting centroids, but it is still a challenging and interesting problem to consider for future work.

ACKERMANN, M. R., MARTENS, M., RAUPACH, C., SWIERKOT, K., LAMMERSEN, C., & SOHLER, C. (2012). StreamKM++: A Clustering Algorithm for Data Streams. Journal of Experimental Algorithmics JEA, 17, 1-31.

AGGARWAL, C. A survey of stream clustering algorithms. Chapman and Hall/CRC. 2013

AGGARWAL, C., HAN, J., WANG, J., & YU, P. S. (2003). A Framework for Clustering Evolving Data Streams, (pp. 81-92).

AMINI, A., WAH, T. Y., & SABOOHI, H. (2014). On Density-Based Data Streams Clustering Algorithms: A Survey. Journal of Computer Science and Technology, 29(1), 116-141.

ARTHUR, D, & VASSILVITSKII, S. (2003). K-means++: The Advantages of Careful Seeding. (pp. 1027-1035). Society for Industrial and Applied Mathematics.

BECKMANN, N., KRIEGEL, H.-P., SCHNEIDER, R., & SEEGER, B. (1990). The R*-tree: An Efficient and Robust Access Method for Points and Rectangles. (pp. 322-331). ACM.

BENTLEY, L & SAXE, J. B. (1980). Decomposable searching problem, Static-to-dynamic transformation. Journal of Algorithms, 1(4):358.

BHATT, R. B., SHARMA, G., DHALL, A., & CHAUDHURY, S. (2009). Efficient Skin Region Segmentation Using Low Complexity Fuzzy Decision Tree Model, (pp. 1-4).

BIFET, A., HOLMES, G., KIRKBY, R., & PFAHRINGER, B. (2010). MOA: Massive Online Analysis. J. Mach. Learn. Res., 11, 1601-1604. Retrieved from http://dl.acm.org/citation.cfm?id=1756006.1859903

BIFET, A., HOLMES, G., PFAHRINGER, B., & GAVALDA, R. (2009). Improving Adaptive Bagging Methods for Evolving Data Streams. (pp. 23-37). Berlin, Heidelberg: Springer-Verlag. Retrieved from http://dx.doi.org/10.1007/978-3-642-05224-8_4

CAO, F., ESTER, M., QIAN, W., & ZHOU, A. (2006). Density-based clustering over an evolving data stream with noise, (pp. 328-339).

CHANDOLA, V., BANERJEE, A., & KUMAR, V. (2009). Anomaly Detection: A Survey. ACM Comput. Surv., 41(3), 15:1-15:58. Retrieved from http://doi.acm.org/10.1145/1541880.1541882

CHAUDHRY, N., SHOW, K., & ABDELGUERFI, M. (2005). Stream data management. Advances in Database system . Vol. 30. Springer.

CHEN, G., & LUO, W. (2015). Clustering Time-Evolving Data Using an Efficient Differential Evolution. In Y. Tan, Y. Shi, F. Buarque, A. Gelbukh, S. Das, & A. Engelbrecht (Eds.), Advances in Swarm and Computational Intelligence: 6th International Conference, ICSI 2015, held in conjunction with the Second BRICS Congress, CCI 2015, Beijing, China, June 25-28, 2015, Proceedings, Part I (pp. 326-338). Cham: Springer International Publishing. Retrieved from https://doi.org/10.1007/978-3-319-20466-6_35

DONGRE, P., & MALIK, L. (2014). A review on real time data stream classification and adapting to various concept drift scenarios, (pp. 533-537).

ERICSON, K., & PALLICKARA, S. (2013). On the Performance of High Dimensional Data Clustering and Classification Algorithms. Future Gener. Comput. Syst., 29(4), 1024-1034. Retrieved from http://dx.doi.org/10.1016/j.future.2012.05.026

GHESMOUNE, M., LEBBAH, M., & AZZAG, H. (2016). State of the art on clustering data streams. Big Data Analytics, 1(1), 13.

GUO, X., YIN, Y., DONG, C., YANG, G., & ZHOU, G. (2008). On the Class Imbalance Problem, 4, pp. 192-201.

GUO, Y., WANG, J., & WANG, K. (2016). BOUNDARY DETECTING ALGORITHM FOR EACH CLUSTER BASED ON DBSCAN. Boundary Detecting Algorithm for Each Cluster based on DBSCAN.

GUTTMAN, A. (1984). R-trees: A Dynamic Index Structure for Spatial Searching. (pp. 47-57). ACM.

HASAN, T. (2014). A Data Mining Approach For Handling Evolving Data Streams. IOSR Journal of Computer Science.

HOTELLING, H. (1931). The generalization of Student's ratio. Annals of Mathematical Statistics, 2 (3): 360378.

JIAWEI, H., & KAMBER, M. (2011). Data Mining: Concepts and Techniques. 3rd Edition. Elsevier.

KHALILIAN, M., & MUSTAPHA, N. (2010). Data Stream Clustering: Challenges and Issues. CoRR, abs/1006.5261. Retrieved from http://arxiv.org/abs/1006.5261

KONTAKI, M., GOUNARIS, A., PAPADOPOULOS, A. N., TSICHLAS, K., & MANOLOPOULOS, Y. (2011). Continuous monitoring of distance-based outliers over data streams, (pp. 135-146).

KRANEN, P., ASSENT, I., BALDAUF, C., & SEIDL, T. (2011). The ClusTree: Indexing Micro-clusters for Anytime Stream Mining. Journal Knowledge and Information Systems, 29(2), 249-272.

LOWRY, C , WOODALL, W. H., CHAMP, C. W., & RIGDON, S. E. (1992). A Multivariate Exponentially Weighted Moving Average Control Chart. Technometrics, 34(1), 46-53.

MAKHOUL, J., KUBALA, F., SCHWARTZ, R., & WEISCHEDEL, R. (1999). Performance Measures For Information Extraction, (pp. 249-252).

MANN, H. B., & WHITNEY, D.  (1947). On a test of whether one of two random variables is stochastically larger than the other. Annals of Mathematical Statistics, 18(1), 50-60.

MINKU, L., & YAO, X. (2012). DDD: A New Ensemble Approach for Dealing with Concept Drift. Knowledge and Data Engineering, IEEE Transactions on, 24(4), 619-633.

NESHAT, M., SEPIDNAME, G., EIZI, A., & AMANI, A. (2015). A New Skin Color Detection Approach based on Fuzzy Expert System. Indian Journal of Science and Technology, 8(21). Retrieved from http://www.indjst.org/index.php/indjst/article/view/50606

OZA, N., & RUSSELL, S. (2011). Experimental Comparisons of Online and Batch Versions of Bagging and Boosting. ACM SIGKDD  Conf. Knowledge Discovery and Data Mining(2001), 359-364.

PIRIM, H., EKCIOUGLU, B., PERKINS, A. D., & YUCEER, C. (2012). Clustering of High Throughput Gene Expression Data. Comput. Oper. Res., 39(12), 3046-3061. Retrieved from http://dx.doi.org/10.1016/j.cor.2012.03.008

ROSSI, P. E., ALLENBY, G. M., & MCCULLOCH, R. (2012). Bayesian Statistics and Marketing. John Wiley & Sons.

SEIDL, T., ASSENT, I., KRANEN, P., KRIEGER, R., & HERRMANN, J. (2009). Indexing Density Models for Incremental Learning and Anytime Classification on Data Streams. (pp. 311-322). ACM.

SHARMA, A., GUPTA, & TIWARI, A. (2016). Improved Density Based Spatial Clustering of Applications of Noise. Mathematical Problems in Engineering.

STAHL, F. T., GABER, M., & SALVADOR, M. (2012). eRules: A Modular Adaptive Classification Rule Learning Algorithm for Data Streams, (pp. 65-78). Retrieved from https://doi.org/10.1007/978-1-4471-4739-8_5

TRAN, L., FAN, L., & SHAHABI, C. (2016). Distance based Outlier Detection in Data Streams.

VELLOSO, E., BULLING, A., GELLERSEN, H., UGULINO, W., & FUKS, H. (2013). Qualitative Activity Recognition of Weight Lifting Exercises. Proceedings of 4th International Conference in Cooperation with SIGCHI (Augmented Human '13). Stuttgart, Germany: ACM SIGCHI.

WANG, H., FAN, W., YU, P. S., & HAN, J. (2003). Mining Concept-drifting Data Streams Using Ensemble Classifiers. (pp. 226-235). New York, NY, USA: ACM. Retrieved from http://doi.acm.org/10.1145/956750.956778

WANG, H., YU, P., & HAN, J. (2010). Mining Concept-Drifting Data Streams. In O. Maimon, & L. Rokach (Eds.), Data Mining and Knowledge Discovery Handbook (pp. 789-802). Springer US.

WANG, S., MINKU, L., GHEZZI, D., CALTABIANO, D., & TINO, Y. (2013). Concept drift detection for online class imbalance learning. The 2013 International Joint Conference on Neural Networks (IJCNN).

Widmer, G., & Kubat, M. (1996). Learning in the Presence of Concept Drift and Hidden Contexts., (pp. 69-101).

ZHANG, T., RAMAKRISHNAN, R., & LIVNY, M. (1996). BIRCH: An Efficient Data Clustering Method for Very Large Databases. SIGMOD Rec., 25(2), 103-114. Retrieved from http://doi.acm.org/10.1145/235968.233324

ZHOU, A., CAO, F., QIAN, W., & JIN, C. (2008, May). Tracking clusters in evolving data streams over sliding windows. Knowledge and Information Systems, 15(2), 181-214. Retrieved from https://doi.org/10.1007/s10115-007-0070-x

1. PhD in Engineering. Computer Engineering Dept., Universidad del Quindío, UQ. Armenia, (Colombia), sjaramillo@uniquindio.edu.co

2. PhD in Computer Science. Engineering Dept. Universidad Pontificia Bolivariana, UPB. Medellín, (Colombia), jorge.londono@upb.edu.co

3. PhD candidate in Engineering. Computer Engineering Dept., Universidad del Quindío, UQ, Armenia, (Colombia), sergio_cardona@uniquindio.edu.co