ISSN 0798 1015

Vol. 39 (# 10) Year 2018. Page 27

Situational modeling of transportation problems: applied and didactic aspects

Modelización situacional de problemas de transporte: aspectos aplicados y didácticos

Sergey BALYCHEV 1; Aleksandr BATKOVSKIY 2; Pavel KRAVSHUK 3; Valeriy TROFIMETS 4; Elena TROFIMETS 5

Received: 26/12/2017 • Approved: 15/01/2017

Contents

1. Introduction

2. Literature Review

3. Methodology

4. Results

5. Discussion

6. Conclusion

Acknowledgement

Bibliographic references

1. Introduction

One of the trends in the modern economic education development is heightened requirements for the mathematical training level of graduates. At the same time, special attention is paid to the practical skill not only to solve typical problems of a computational nature, but also various case problems, in solving which, the analytical component assumes a leading role. The latter aspect is closely related to the students’ ability to make decisions under the influence of random internal and external factors, to analyze the current and predict the future state of the economic systems and processes under study based on application of modern mathematical models and methods. All this sets rather high requirements to the mathematical training level of modern management specialists. At the same time, the study of mathematical disciplines is intended to reveal not only the content of the mathematical knowledge proper, but also to establish close integrative links with special disciplines, especially those that are accompanied by the solution of professionally-oriented problems using knowledge-based economic-mathematical models and methods.

However, it should be mentioned that having an insight into mathematical methods and models is not a sufficient condition for solving real economic problems, especially on a large scale. Therefore, along with studying the principle of the methods themselves, it is especially important for students of economic specialties to master techniques for computer simulation of real world situations. Successfully mastered, such technologies lay the groundwork for the knowledge-based methods of mathematical economic modeling not to be left behind in the school, but instead to prove to be in demand for validating managerial decisions within the framework of real world situations. Thus, the computer simulation technologies implement the paradigm ‘mathematics helps economics, while computer science helps mathematics’. The implementation of such a paradigm allows the focus of attention to be shifted from studying algorithmic features of the methods to the issues of building and modifying models that would reflect real world situations.

The transportation problem considered in the article subsumes a wide class of mathematical programming problems. Various statements of these problems and methods for their solution are widely represented in numerous literature sources (Chong & Zak, 2013; (Lange, 2013; Hillier & Lieberman, 2014; Zolotaryov, 2014; Fujisawa et al., 2015) and others. Nevertheless, the possibility of an effective solution with the help of mathematical programming methods for various sector specific tasks still generates much interest among researchers (Craven & Islam, 2005;Bahmani, et al., 2013; (Beck & Eldar, 2013; Eiselt & Sandblom, 2013; Batkovskiy et al., 2016) and so on.

Typically, a transportation problem is associated with a transfer of cargo from suppliers to consumers. Along with that, it can be used to solve other tasks that are not directly related to transit of goods. Examples of such tasks are: an optimization of fuel and energy balance, an optimal distribution of agricultural crops, an optimal production location, an optimal machine loading plan, and a number of other problems (Wagner, 1975; Byrne, 2014; Durea & Strugariu, 2014; Arora, 2015; Dedu & Şerban, 2015;Ghandar et al., 2016), etc.

The application of mathematical economic transportation models in practical activities is inextricably intertwined with their implementation at the program level. In addition, it is not only application of specialized software solutions that is of interest, but also an analyst manager’s ability to build a mathematical economic and computational model of a controlled logistical system using standard software tools, in particular, the MS Excel spreadsheet.

The works by Batkovskiy et al. (2017), Alastair (2015), Avon (2015), Goossens (2015), Benninga (2014), Jablonsky (2014), Fairhurst (2012), Charnes (2012), Taha (2010), Lai et al. (2010) and others focus on issues related to the construction of optimization, balance, and probabilistic models of economic systems in the MS Excel environment.

The didactic aspects of introducing information technologies in the educational process, including computer simulation technologies, are considered in the works by Kuzhel‘ and Kuzhel’ (2002), Rutten, Van Joolingen and Van Der Veen(2012), Druzhinina, Masina and Vorontsova (2015), Lakkala & Ilomäki(2015), etc.

3.1. Didactic aspects of computer simulation in the economics students’ learning process

At the present time, mathematical simulation has found extensive application not only in carrying out theoretical research of economic systems and processes, but also in the solution of many real-life management problems in the field of economics and finance. The latter aspect is largely due to the development of software simulation source environments that allow a nonprogrammer user to translate mathematical economic models from a classical alphanumeric description into a computerized one. Thus, an operating user has received affordable and effective tools for constructing and analyzing real-world situation models, which plays a decisive role for practical activities.

In turn, the needs of modern economic science and practice have served as the major premise for a widespread acceptance of computer simulation technologies in the educational process in higher economic educational institutions. At the same time, two main applications of these technologies can be distinguished. In the first application, computer simulation is considered as a means of transferring the articulated part of knowledge to students, while within the second scope – as a means of transferring the non-articulated part of knowledge.

The articulated part of knowledge is a part of knowledge that is relatively easy to structure and can be transferred to a learner with the help of separate pieces of information (text, graphics, video, etc.). To support the process of acquiring the articulated part of knowledge, educational software and methodologies are used, whereby learning content is basically presented in a declarative form. Such software and methodical tools include: electronic textbooks, electronic compendia of lectures, automated training courses, and other software and methodologies that allow learners to transfer individual pieces of structured learning information. In software methodical means of the declarative type, computational models normally play an auxiliary role and are intended to graphically present the backbone of the studied economic objects (processes) to learners.

The knowledge component, primarily based on a person’s practical experience and intuition, has been named the non-articulated part of knowledge. This part of knowledge cannot be transferred to a learner in the form of a finished piece of information, but instead is ‘extracted’ by them in the course of independent cognitive activity while solving practical problems. To support the process of acquiring the non-articulated part of knowledge, educational software and methodologies are used, whereby educational content is basically presented in a procedural form. This form assumes that a learner, in the course of a determinated or freewheeling educational research, acquires knowledge of the properties of the objects or processes under study. The educational software and methodologies of the procedural type include: computer-based practical exercises, virtual laboratory classes, computer simulators, and other software methodical tools that allow learners to develop skills in research and analytical work. Generally, a basis for working with such systems is formed by a certain methodology for constructing a computational model of the object (the process) under study and a subsequent work with the model.

Experience has proven that among a wide range of modeling software systems for economics students, the programs they will use in future professional activities are of special interest. It is this practical aspect that draws special attention to universal table processors, in particular, MS Excel. Considering MS Excel as an environment for constructing and analyzing optimization models is due to a number of other practical considerations.

First, this software product is normally quite familiar to students from the school days and continues to be studied in an extended format in computer science classes in higher school. Second, MS Excel is installed on computers in the vast majority of organizations, which is crucially important in the aspect of its practical application in future professional activities, as already noted. Third, it has a developed library of functions of various categories, which allows non-programmers to design fairly flexible models for solving a wide range of professionally oriented business problems. Fourth, MS Excel has an open architecture that allows one, when necessary, to expand its functionality by developing custom functions and VBA software add-ins. Fifth, due to the advanced mechanisms of data import/export, MS Excel integrates well with a large number of software products, including cloud solutions.

The practice of using the MS Excel spreadsheet as an environment for construction and subsequent analysis of optimization models has confirmed its high didactic potential. The use of MS Excel in modeling various case problems becomes especially convenient when the focus of attention is shifted from the computational aspects of a problem solution to its applied research.

3.2. Computer simulation of transportation case problems

Transportation problems hold a specific place among mathematical programming problems. Their description is usually associated with distribution of some cargo in a certain transportation system. At the same time, there are other descriptions related to logistics in the energy, information, financial, and other systems (Craven & Islam, 2005; Cornuejols & Tutuncu, 2006; Urubkov, 2006; Eiselt & Sandblom, 2013; Ouardighi & Kogan, 2013).

In mathematical description, transportation problems represent, like most mathematical programming problems, optimization models that include an objective function and a set of constraints in their structure. Most of these models are linear programming problems of a special form, a classical transportation problem being the most common of them. Its formulation is as follows.

There are n consumers and m suppliers of a homogeneous cargo. The suppliers have cargo stocks in the volume of a1, а2, …,аm. The consumers are characterized by cargo orders in the volume of b1, b2, ...,bn. Also, transportation cost of one cargo unit from the i-th supplier to the j-th consumer is known, which is denoted by сij. What can be understood as transportation cost is tariffs, distances, time, fuel consumption, etc. The variables xij, that is, the volume of cargo transportation from the i-th supplier to the j-th customer, are the unknown variable in the transportation problem. It is required to develop a transportation plan with the lowest cost possible.

The initial data of the transportation problem are usually tabulated as follows (Table 1):

Table 1
A transportation problem input spreadsheet

Along with the tabular format, the matrix format of recording the original data has gained widespread acceptance:

If software is used in the educational process to solve a transportation problem, the tabular recording format is used in tabular processors (normally, MS Excel), while the matrix recording format is used in mathematical software (usually Mathcad).The mathematical model of a transportation problem in its classical description has the following form:

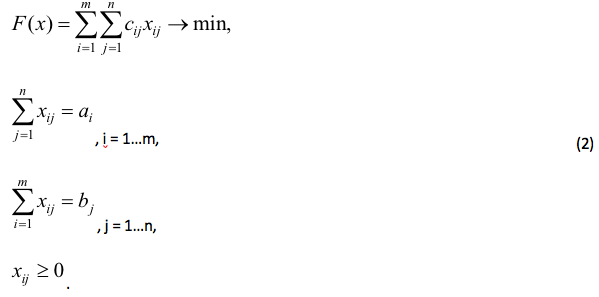
Since the problem (2) belongs to the class of linear programming problems, it can be solved using the simplex method. However, a special kind of constraint system makes it possible to use simpler methods to solve it. Thus, to develop an agenda to solve the problem (2), the northwest corner method is the best known. The least-cost method and Vogel method can be used as well(Wagner, 1975; Taha, 2010). To improve the agenda to the optimum, the distribution method or the potential method is normally used.

However, it should be noted that understanding the mathematical nature of methods is an important but not sufficient condition for solving real-world transportation problems. Therefore, along with their study, it is advisable to use a computer technology enabling one to promptly simulate various transportation situations. At the same time, the focus of attention, as noted above, is shifted from the computational aspects of the problem solution to its applied research, which is especially important for students majored in economics.

Let us consider the applied aspects of constructing transportation models.

The study of transportation models in an academic institution normally begins with the classical model consideration (2). In this model, the relation (3) is satisfied, that is, the sum of suppliers’ stocks is equal to the sum of customers’ orders:

Therefore, the model (2) is also referred to as a balanced transportation problem or a closed-ended transportation problem.

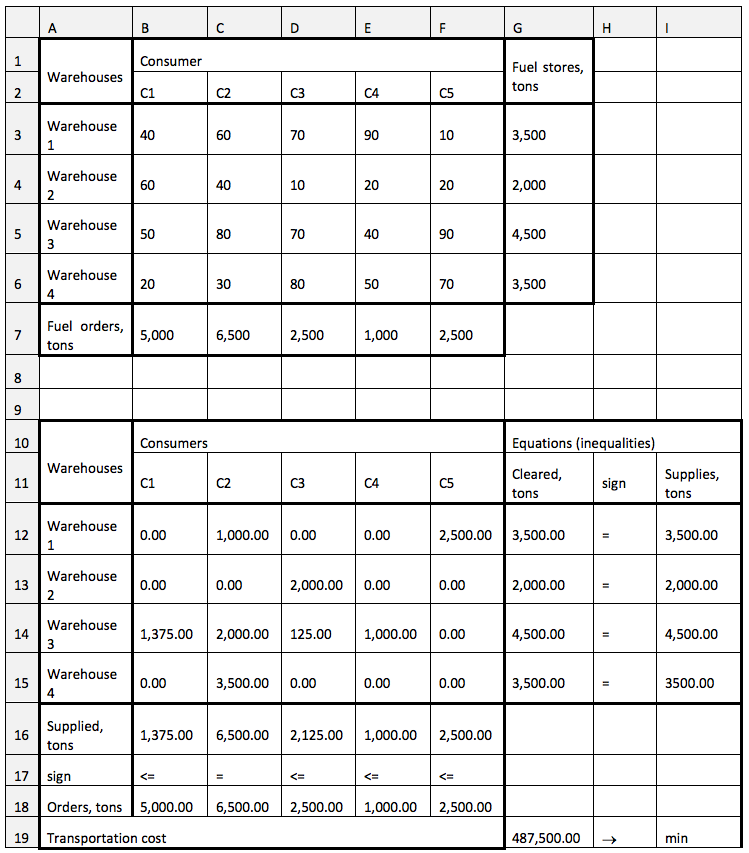
If the equality (3) is not satisfied, the problem is referred to as unbalanced or an open-ended problem. Unbalanced transportation problems can fall into two types:

Table 2
Transportation model – situation 1

The next group of important real world situations is associated with blocking transportation traffic on certain routes or, conversely, with the transit of fixed volumes of cargo on specified routes (transportation under contracts).

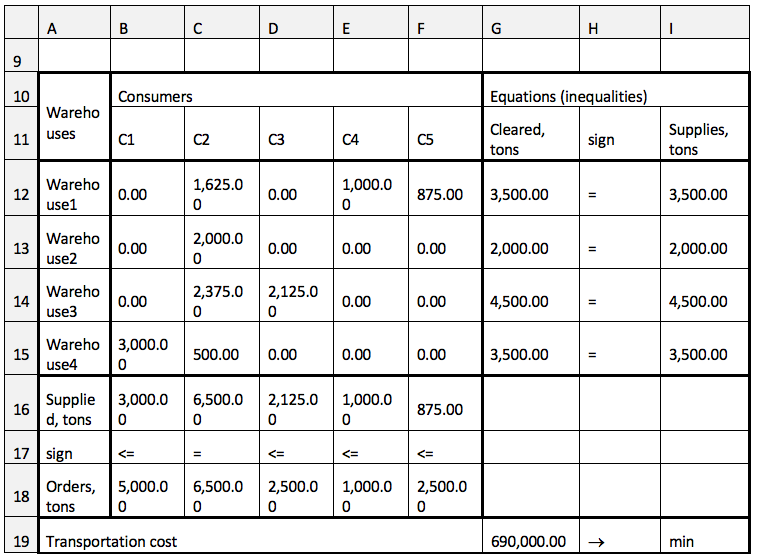
Table 3 shows an example of the transportation problem solution for the traffic blocking situation Warehouse2 – Consumer3, Warehouse3 – Consumer1, and transportation of fixed volumes of cargo along the routes Warehouse4 – Consumer1 (3,000 tons of fuel) and Warehouse1 – Customer4 (1,000 tons of fuel). The problem solution is given in Table 3.

Table 3
Transportation model – situation 2

It should be noted that only the two transport models given above cover the entire list of transportation problem statements that can be considered in the learning process if the focus is on their manual solution. Using the computer simulation technology, students manage to consider these situations in half an hour on average. Thus, time is released to consider not only other transportation models, but also optimization problems encountered in practical activity, which are fundamentally different in the description. At the same time, the emphasis is shifted to students’ analytical activity related to construction of mathematical and computational models adequate to real-life situations.

In the study of transportation models, simulation of various resource allocation mechanisms, in particular, the mechanism of direct priorities, the mechanism of reverse priorities, the competitive mechanism, the mechanism of open-book management is of practical interest. These mechanisms are of great generality and are applicable to other types of resource allocation problems.

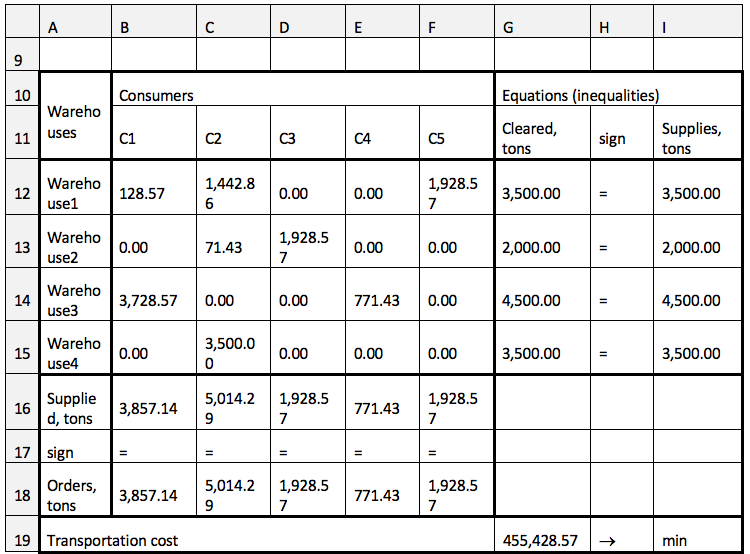
The solution to the transportation problem employing the scheme of pro rata ‘cut-back’ of orders (a variation of the mechanism of direct priorities) is presented in Table 4.

Table 4
Transportation model – situation 3

The situations addressed and the respective mathematical and computational models positively cannot cover all the variety of those numerous real-life situations that occur in transport logistics. Nevertheless, they can be considered as basic (typical) situations and models that can be used to teach classes on operations research methods in the managers’ learning process. The proposed models can also serve students as starting points for further research. Within the framework of transport logistics, cargo transportation with regard to vehicle capacity, multi-commodity transportation, transshipment, and many other trends can be such lines of research.

3.3. Methodology for assessing the didactic efficiency of computer simulation technology

To assess the didactic efficiency of educational technologies, a pedagogical experiment is normally carried out. The point of performing almost all of the experiments known today is similar: a comparison of two groups of educatees is made; one of them is trained using a new technology (experimental group), while the other one is trained without the use of such technology (control group), Fig. 1.

Figure 1
Organization chart of a pedagogical experiment

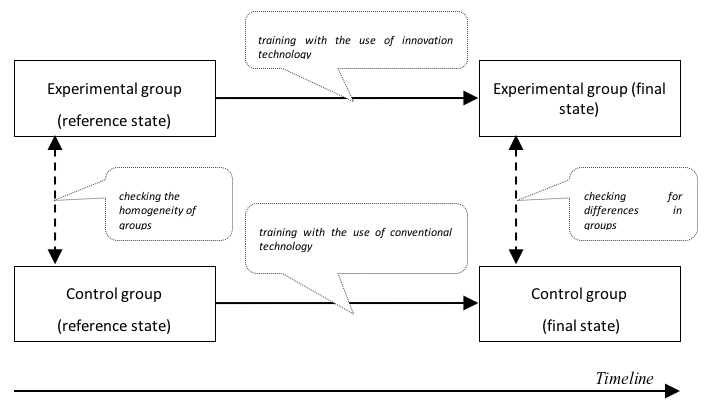
A pedagogical experiment was conducted at the St. Petersburg University of State Fire Service of EMERCOM of Russia at the Economics and Law Faculty as part of training sessions on the discipline ‘Fundamentals of Mathematical Simulation of Social and Economic Processes’. The experimental and control groups were formed out of six study groups in such a way that they included students with approximately the same level of mathematical training (20 students with high, medium, and low levels of mathematical training in each group). The groups were formed based on the students’ marks received in the discipline ‘Higher Mathematics’. The homogeneity of the groups was verified on the basis of Mann-Whitney U test.

In the design of the experiment, a hypothesis was advanced on two factors impacting the quality of teaching material retention: the preliminary mathematical training of educatees and the learning technology (with and without the use of computer simulation technology). In order to minimize the influence of other factors, classes in the study groups were given by the same teacher using similar methods, except that in three study groups (whereby the experimental group was formed), the students were trained using workshops developed to implement the computer simulation technology.

After completion of the course in the study groups, the students’ final grades were summarized in a statistical complex the methods of mathematical statistics were used to process.

In pedagogical research practice, parametric and nonparametric methods for testing statistical hypotheses based on procedures for calculating respective statistics have become the most frequently used. Parametric tests include Student’s test, Cochran-Cox test, Paulson test, Walsh test, etc. Nonparametric criteria include Mann-Whitney test, Hagi test, Van-der-Waerden test, Quenouille test, etc. (Kobzar, 2006; Carvalho & Solomon, 2012).

Nonparametric methods are used when there is no sufficient evidence to make an assumption of a normal distribution of the data processed. The merits of these methods include the fact that they do not require complicated computational calculations.

In the event there are sufficient grounds for assuming a normal distribution of the groups under study, parametric methods should be used, since they have a greater statistical power than nonparametric methods.

Figure 2 shows an algorithm for choosing a method of processing a statistical complex with the pedagogical experiment results.

Figure 2
The algorithm for selecting a method to process statistical complex

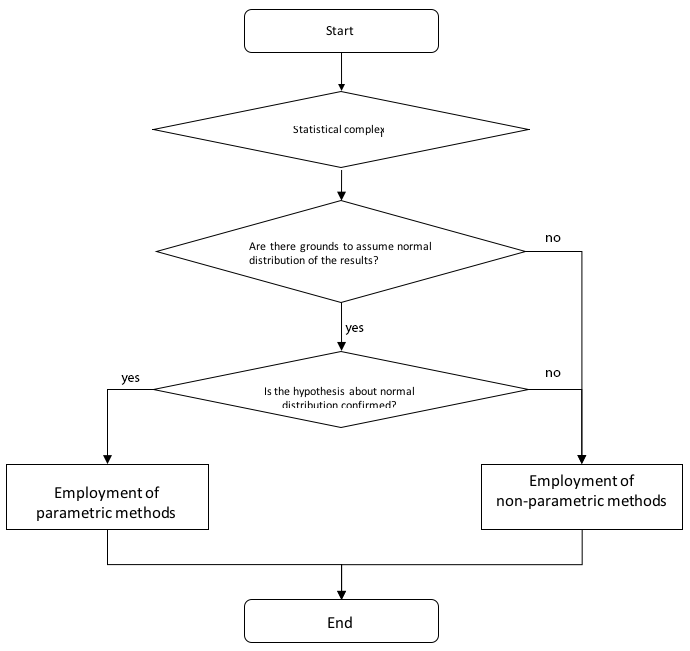
In the experiment, a hypothesis was put forward on a normal distribution of the groups under study. To test the hypothesis, Pearson’s chi-squared test (c2) was used. At the significance level a=0.05, the hypothesis was confirmed, which allowed for the use of parametric methods for further research. The analysis-of-variance method was chosen as such, its research value being in the possibility not only to confirm (or disprove) the difference between the compared groups, but also to reveal the cumulative effect of the factors, the effect of each factor regulated in the experiment, as well as combinations of factors with each other on the resultative feature. Since the effect of two factors (factor A – the level of preliminary mathematical training of students and factor B – the use of computer simulation technology in the learning process) was taken into account in the experiment, the method of two-way analysis of variance was used.

Table 4 shows parameters for the statistical complex to be processed by the method of two-way analysis of variance.

Table 4
Parameters of the statistical complex

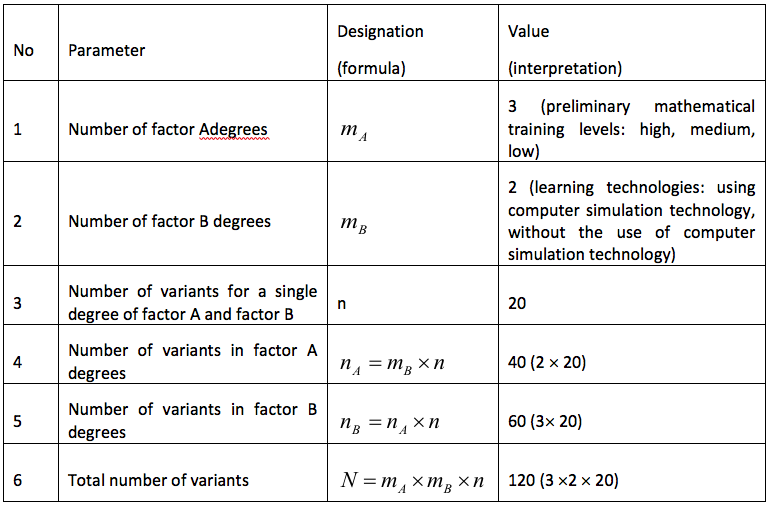
Table 5 shows the main results of statistical analysis of the experimental results.

Table 5
The main results of statistical analysis of the experimental results

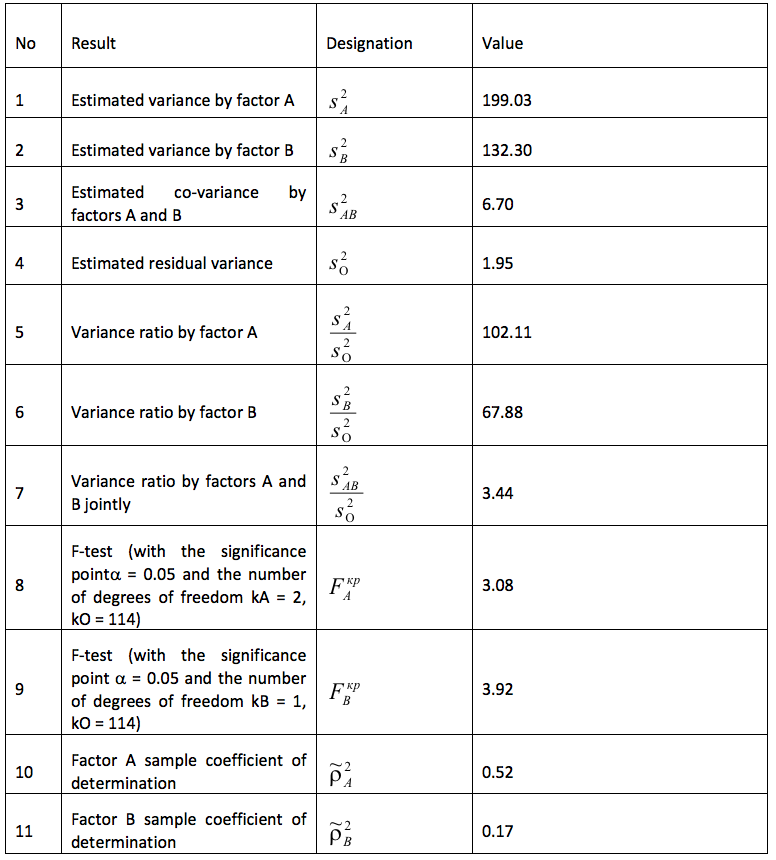
Since the variance ratio by factor A is greater than the calculated value of F-test (102.11> 3.08), at the significance level of a= 0.05 it can be assumed that the level of preliminary mathematical training influences the quality of the educational material retention in the discipline ‘Fundamentals of Mathematical Simulation of Social and Economic Processes’. Calculation of the sample coefficient of determination by factor A makes it possible to establish that about 52% of the total sample variation of grades is associated with the influence of this factor.

Since the variance ratio by factor B is greater than the calculated value of F-test (67.88> 3.92), at the significance level of a = 0.05 it can be assumed that the learning technology based on the development of situational computational models also has a meaningful positive effect on the quality of learning material retention. Calculation of the sample coefficient of determination by factor B allows one to establish the degree of this influence – about 17% of the total sample variation of grades.

A survey among students upon completion of the course with the use of computer simulation technology makes it possible to suggest that this technology does not only generate professional interest, but also contributes to the activation of psychological learning mechanisms.

In psychology, the following learning mechanisms are the best known: the behavioristic learning theory, the associative reflex acquisition theory, the theory of stage-by-stage formation of mental actions, the theory of algorithmic thinking formation, and the theory of lateral thinking formation (Bono, 1997).

Designing educational content with support for the process of acquiring the non-articulated part of knowledge makes it necessary to pay special attention to the theory of algorithmic (operational) thinking formation and the theory of lateral (creative) thinking formation. In psychological research, creative thinking is compared with the associative mechanism and intuition, and operational thinking – with the generalization mechanism. These mechanisms are fundamentally different, but there is interaction between them, its enhancement producing a positive effect (Rutten et al., 2012). This effect is especially evident in the work of experienced experts, consultants, and analysts with many years of experience. A number of psychological studies have shown that enhancing the interaction between the associative mechanism and the generalization mechanism produces a meaningful positive effect on the learning process as well. Thus, in work by (Kuzhel ‘& Kuzhel’, 2002), results of experimental training with the use of computer simulation technology are provided. The technology was investigated by the authors as a means of enhancing the interaction between the psychological learning mechanisms. The outcome of the experiment showed that 49% of the respondents noted an activation of analytical thinking, 28% of the respondents –an activation of the ability to systematize information, and 45% of the respondents – an activation of the ability to draw informed conclusions. Also, 28% of the respondents noted that the construction of computational models required them to find out-of-the-box creative solutions to the full, and 29% – to some extent.

Thus, psychological studies show that the learning environment created by computer simulation technologies does not only support acquisition of the non-articulated part of knowledge, but also contributes to the development of both operational and creative thinking in educatees (Druzhinina et al., 2015; Lakkala & Ilomäki, 2015).

The modern paradigm of specialists’ training in management is based on two main attitudes to modern management and, accordingly, two basic approaches to mastering it. The first approach –empirical (or the approach of adaptations and analogies)– relies on analysis of numerous case studies and real-life managerial situations. The second approach –analytical (or rational) approach – relies on development of analytical abilities in managers.

According to the authors, the randomness and uncertainty inherent in analytical management problems complicate the use of the first approach to solve them and determine the expediency to make active use of the second one. As a result, the expertise and skills to substantiate managerial decisions on the basis of building computational models reflecting the essential features of the analyzed real-life situations acquire a special significance for present-day analyst managers. In this case, an analyst manager acts as sort of a designer who creates conceptual schemes for solving managerial problems. The basis for constructing such schemes is information provision, mathware, and software for decision making support systems. To solve intricate problems, a complex application of several instrumental methods and systems may be required. In this regard, an integration of analytical and simulation models is of practical and didactic interest. The latter can make a difference for an analyst when there are difficulties associated with formalization of business processes. The development of multi-method situational modeling concept in recent years has led to an increased interest in it both from practicing analysts and from the academia. Therefore, one can expect that along with the methods of analytical simulation, there will be a growing need for studying situational modeling methods, in particular, system dynamics, discrete event and agent-based modeling.

The study was conducted with support from the Russian Foundation for Basic Research (RFBR project No. 16-06-00028).

Alastair, D. J. (2015). Mastering Financial Mathematics in Microsoft Excel. (3rd ed.) FT Press, pp: 419.

Arora, R.K. (2015). Optimization: Algorithms and Applications. CRC Press, pp: 466.

Avon, J. (2015). The Basics of Financial Modeling. Apress, pp: 248.

Bahmani, S., Raj, B. and Boufounos, P. (2013). Greedy sparsity-constrained optimization. Journal of Machine Learning Research, 14, 807–841DOI:10.1109/ACSSC.2011.6190194

Batkovskiy, A.M., Semenova, E.G, Trofimets, V.Ya., Trofimets, E.N., & Fomina, A.V. (2017). Statistical simulation of the break-even point in the margin analysis of the company. Journal of Applied Economic Sciences. Romania: European Research Centre of Managerial Studies in Business Administration, XII, 2(48), 558-571. Retrieved from https://www.ceeol.com/search/article-detail?id=532542.

Batkovskiy, A.M., Semenova, E.G, Trofimets, V.Ya., Trofimets, E.N., & Fomina, A.V. (2016). Method for Adjusting Current Appropriations under Irregular Funding Conditions. Journal of Applied Economic Sciences. Romania: European Research Centre of Managerial Studies in Business Administration, XI, 5(43), 828-841. Retrieved from https://www.ceeol.com/search/article-detail?id=534283

Beck, A., Eldar, Y.C. (2013). Sparsity Constrained Nonlinear Optimization: Optimality Conditions and Algorithms. Society for Industrial and Applied Mathematics Journal on Optimization, 23(3), 1480-1509 DOI: 10.1137/120869778

Benninga, S. (2014). Financial Modeling. The MIT Press, pp: 1143. 

Bono, E. (1997). Lateral'noe myshlenie [Lateral thinking]. Sankt-Petersburg, Piter Publishing, pp: 320. [in Russian].

Byrne, C.L. (2014). A First Course in Optimization. N.-Y.: Taylor & Francis Group/CRC, pp: 286.

Charnes, J. (2012). Financial Modeling with Crystal Ball and Excel. 2nd Edition. John Wiley & Sons, pp: 314.

Chong, E.K.P. & Zak, S.H. (2013). An Introduction to Optimization. 4th ed. Wiley, pp: 640.

Cornuejols, G. & Tutuncu, R. (2006). Optimization Methods in Finance. Pittsburgh. Carnegie Mellon University, pp: 349.

Craven, B.D., Islam, S.M.N. (2005). Optimization in Economics and Finance: Some Advances in Non-Linear, Dynamic and Stochastic Models. Springer, pp: 163.

Dedu, S. and Şerban, F. (2015). Multiobjective Mean-Risk Models for Optimization in Finance and Insurance. Procedia Economics and Finance, 32, pp. 973-980. https://doi.org/10.1016/S2212-5671(15)01556-7

Druzhinina, O., Masina, O., Vorontsova, V. (2015). Use of Computer Technologies in Education and Scientific Research for Training Economists. Asian Social Science,11, pp. 45-49 doi:10.5539/ass.v11n11p45

Durea, M. & Strugariu, R. (2014). An Introduction to Nonlinear Optimization Theory. De Gruyter, pp: 327.

Eiselt, H.A., & Sandblom C.-L. (2013). Operations Research: A Model-Based Approach. Springer, pp: 451.

Fairhurst, D.S. (2012). Using Excel for Business Analysis. Wiley. pp: 320.

Fujisawa, K., Shinano, Y. & Waki, H., 2015. Optimization in the Real World: Toward Solving Real-World Optimization Problems. Springer. pp: 194.

Ghandar, A., Michalewicz, Z. and Zurbruegg, R. (2016). The relationship between model complexity and forecasting performance for computer intelligence optimization in finance. International Journal of Forecasting, 32(3), 598-613. https://doi.org/10.1016/j.ijforecast.2015.10.003

Goossens, F. (2015). How to Implement Market Models Using VBA. Wiley. pp: 312.

Hillier, F.S. & Lieberman, G.J. (2014). Introduction to Operations Research. McGraw Hill Higher Education, pp: 1050.

Jablonsky, J. (2014). MS Excel based Software Support Tools for Decision Problems with Multiple Criteria. Procedia Economics and Finance, 12, 251-258. https://doi.org/10.1016/S2212-5671(14)00342-6

Kobzar', A.I. (2006). Prikladnaja matematicheskaja statistika. [Applied mathematical statistics]. Moscow: Fizmatlit, pp: 816. [in Russian].

Kuzhel', S.S., & Kuzhel', O.S. (2002). Informacionnye tehnologii – sredstvo razvitija sistemnogo tvorcheskogo myshlenija [Information technologies - a means of developing systemic creative thinking]. Obrazovatel'nye tehnologii i obshhestvo - Educational Technology & Society, 5(1), 264-275 [in Russian].

Lai, D.C.F., Tung, H.K.K., Wong, M.C.S., et al. (2010). Professional Financial Computing Using Excel and VBA. Wiley, pp: 352.

Lakkala, M., Ilomäki, L. (2015). A case study of developing ICT-supported pedagogy through a collegial practice transfer process. Computers and Education, 90, 1-12. https://doi.org/10.1016/j.compedu.2015.09.001

Lange, K. (2013). Optimization. Springer, pp: 540.

1. Department of Corporate Finance and Corporate Governance, Financial University under the Government of the Russian Federation, Moscow, Russia. Bs0209@inbox.ru

2. Joint Stock Company ‘Central Research Institute of Economy, Management and Information Systems ‘Electronics’, Moscow, Russia. batkovsky@yandex.ru

3. Joint Stock Company ‘Research and Test Center ‘INTELELEKTRON’, Moscow, Russia. p.kravchuk@mail.ru

4. Department of Information Systems and Computing, Saint-Petersburg Mining University, St. Petersburg, Russia. zemifort@inbox.ru

5. Department of Higher Mathematics and System Modeling of Complex Processes, Saint-Petersburg University of State Fire Service of EMERCOM of Russia, St. Petersburg, Russia. еzemifort@inbox.ru