

 Vol. 39 (Nº 10) Año 2018. Pág. 6
Vol. 39 (Nº 10) Año 2018. Pág. 6
Wbeimar CIFUENTES Robledo 1; Jhony Alexander VILLA-OCHOA 2
Recibido: 18/10/2017 • Aprobado: 19/11/2017
3. Modos de pensamiento en algunas tareas del álgebra escolar: algunas características
RESUMEN: Se analizan las respuestas de un conjunto de profesores de matemáticas a tres tareas que involucraban diferentes formas de representación. Se usó el referente teórico de los modos de pensamiento propuesto por Sierpinska para identificar conexiones entre modos de pensamiento sintético y analítico. Se analizaron los datos provenientes de los documentos y de las manifestaciones orales que los profesores produjeron al enfrentarse a las tareas. Los resultados muestran un predominio de procesos algebraicos y pocas estrategias que conjuguen los modos de pensamiento. |
ABSTRACT: This paper analyses responses from mathematic's teachers to three tasks involving different forms of representation. The modes of thinking by Sierpinska were the theoretical reference used to identify connections between synthetic and analytical modes of thinking. Data to be analyzed derived from documents and oral expressions produced by these teachers. Results evidence the predominance of algebraic processes and of a few strategies to combine these modes of thinking. |
La discusión sobre la relación entre el conocimiento y la profesión docente es compleja, pues el conocimiento es en sí mismo un insumo en el que se centran los propósitos de la enseñanza (Rowland, 2014). En coherencia con este planteamiento, el conocimiento, actitudes, consideraciones y razonamientos que los profesores posean frente a las matemáticas y su enseñanza es importante para comprender con mayor profundidad los fenómenos de aprendizaje de las matemáticas. Al respecto, en la literatura han emergido estudios que se centran en el papel que desempeñan las acciones del profesor en los aprendizajes de los estudiantes (Cantoral y Farfán, 2003).
En el contexto colombiano los profesores deben superar la visión de un currículo que se centre solo en procedimientos y contenidos, en cambio, deben promover el desarrollo del pensamiento matemático en la Educación Básica y Media. El conocimiento matemático incluye la referencia al conocimiento conceptual y conocimiento procedimental, entre otros. En cuanto al primero se afirma que: “está más cercano a la reflexión y se caracteriza por ser un conocimiento teórico, producido por la actividad cognitiva (…)”. El segundo “está más cercano a la acción y se relaciona con las técnicas y las estrategias para representar conceptos (…)” (Colombia-MEN, 2006, p.50). En este planteamiento es posible señalar que el conocimiento conceptual involucra los razonamientos, los diferentes modos de pensar, representar y dar significado a los objetos matemáticos, en tanto que el conocimiento procedimental está relacionado con un razonamiento que incluye los modos de actuación y de operar con dichos objetos y de los fundamentos que soportan los algoritmos.
En la literatura internacional existen diferentes perspectivas teóricas para referirse al conocimiento de los objetos matemáticos; por ejemplo Sfard (1991) establece que los conceptos matemáticos radican en una dualidad: la concepción operacional y la concepción estructural. La concepción operacional permite una mirada dinámica y secuencial a los conceptos; se relaciona con los algoritmos, procesos y acciones que ocurren a nivel físico o mental. De otro modo, una concepción estructural ofrece una mirada estática e instantánea al concepto, es más abstracta y menos detallada que la mirada operacional. Según Sfard, el paso de una concepción operacional a una estructural se da a partir de un proceso de reificación.
Por su parte, Sierpinska (2000) señala que en las matemáticas escolares debe promoverse diferentes modos de pensar los objetos matemáticos, entre ellos, el pensamiento sintético-geométrico, analítico-aritmético y analítico- estructural. En una interpretación de su trabajo, puede colegirse la necesidad de trascender los aspectos procedimentales para que los estudiantes conjuguen diferentes maneras de pensar y las coloquen en acto al dar significado a los objetos matemáticos y solucionar problemas.
En coherencia con la anterior interpretación, a través de sus prácticas escolares, los profesores cumplen un papel fundamental en la creación de ambientes de aprendizaje que superen la clásica visión de resolución de tareas estereotipadas centradas en procedimientos rutinarios (Villa-Ochoa, 2015), y centren las prácticas en la preparación de los estudiantes en distintas maneras de pensar y actuar con las matemáticas que les enseñan.
En este sentido, en este artículo se estudia las maneras en que un conjunto de profesores se enfrenta a tareas en las que intervienen los diversos modos de pensamiento. Los aportes que Sierpinska (2000) indican que los modos de pensamiento ofrecen a la comprensión de los objetos matemáticos un fuerte componente analítico, geométrico y visual y que sus características no son jerárquicas, es decir, se complementan para alcanzar la comprensión. En particular, este estudio se enfocó en responder a la pregunta ¿Cuáles características de los modos de pensamiento evidencian los profesores de matemáticas cuando solucionan tareas de tipo algebraico?
Sierpinska (2000) ofrece un constructo en el que describe tres modos de pensamiento matemático. Este constructo nació en el seno del estudio del razonamiento de los estudiantes sobre conceptos del álgebra lineal; sin embargo, algunos estudios extienden su uso a conceptos matemáticos fuera del ámbito de esta área. Por ejemplo, Bonilla y Parraguez (2013) lo usaron para estudiar la comprensión de estudiantes sobre el concepto de elipse. En su estudio, las autoras sugieren que aproximarse a un concepto solo a través de ecuaciones cartesianas es insuficiente para su comprensión. Según sus resultados, se requiere que al estudiarlo se resalten otras formas de pensamiento.
Para Sierpinska (2000), el pensamiento teórico “se caracteriza por una reflexión consciente sobre los medios semióticos de representación del conocimiento y por sistemas de conceptos (sistemas conceptuales) en vez de agregados de ideas” (p. 211, traducción de los autores), es decir que está basado en conexiones lógicas y relaciones de conceptos con otros más generales. En contraste, el pensamiento práctico enfatiza en la manipulación y aplicación de operaciones y signos sobre elementos matemáticos, y se relaciona con el pensamiento analítico. Para la autora, el pensamiento teórico y pensamiento práctico están determinados por tres modos de pensamiento, a saber, sintético-geométrico (pensamiento práctico); analítico-aritmético y analítico-estructural; estos dos últimos tienen que ver con el pensamiento teórico.
En el modo de pensamiento analítico-aritmético, Sierpinska (2000) señala que los objetos matemáticos son dados por relaciones, operaciones y procedimientos con números y variables. En el caso del modo sintético-geométrico, los objetos matemáticos se definen por características geométricas a partir de funciones, coordenadas, vectores, entre otras, y son representados por medio de imágenes. En el analítico-estructural, los objetos matemáticos se explican a partir de propiedades, características, axiomas o definiciones más generales.
Otra diferencia entre el modo sintético y analítico (aritmético y estructural) es que en el modo sintético los objetos son dados, en cierto modo, directamente a la mente que luego trata de describirlos; mientras que, en el modo analítico se les da indirectamente, de hecho, sólo son construidos por la definición de las propiedades de sus elementos (Sierpinska, 2000).Una manera de favorecer la comprensión de un objeto o concepto matemático es mediante la promoción de transiciones e interacciones entre estos tres tipos de pensamiento.
A diferencia de otros marcos teóricos, los modos de pensamiento no constituyen diferentes etapas del desarrollo del pensamiento algebraico, en otras palabras, son igualmente necesarios en la comprensión de un concepto (Parraguez y Bozt, 2012). Los modos de pensamiento se consideran como fruto de “una superación de dos obstáculos o dos posiciones dogmáticas opuestas: una, que rechaza los números dentro de la geometría y la otra, que rechaza que la ‘intuición geométrica’ pueda ser llevada a un dominio puramente aritmético” (Parraguez y Bozt, 2012, p. 54).
En el estudio participaron un total de diez profesores de matemáticas que ejercían en colegios públicos de subregiones aisladas de las principales ciudades en Colombia. Los profesores se desempeñaban en los niveles de Educación Básica Secundaria (11-15 años) y Media (15-17 años). La mayoría tenía formación universitaria como profesores de matemáticas. Ellos participaron de manera voluntaria en un conjunto de dos sesiones de trabajo de cuatro (4) horas cada una. En la primera sesión se discutió la teoría de los modos de pensamiento de Anna Sierpinska y la manera cómo desarrollaban los temas al interior de la clase; en la segunda sesión se propusieron tres (3) tareas de matemáticas con las cuales, además de su solución, se promovió la realización de discusiones y producciones escritas. Los participantes disponían de elementos como lápiz, regla, papel y computador con software (Geogebra).
Para la recolección de los datos se propuso a los profesores un conjunto de tres (3) tareas. Estas tareas se eligieron por ofrecer una variedad de maneras de presentar información (gráfica, algebraica, verbal) y permitir diferentes caminos de solución. Además, representan el tipo de tarea que circula en libros de texto de matemáticas en el medio.
En la primera tarea se presentó la gráfica de una cónica y se les pidió que argumentaran a qué tipo de cónica correspondía. La tarea tenía como propósito indagar sobre dos aspectos de interés. Por un lado, el tipo de razonamiento utilizado, y por otro, la idea de demostración que se puede derivar de la tarea.
El enunciado de la primera tarea fue: A continuación se muestra en la figura la representación gráfica de una cónica. Demuestre que se trata de una parábola cuyo vértice coincide con el centro de coordenadas del plano cartesiano.
Fig. 1
Representación gráfica de una cónica

En la segunda tarea se ofreció un enunciado verbal y se solicitó la construcción de otro tipo de representaciones. El enunciado fue: “Represente matemáticamente el siguiente enunciado: ‘un número elevado al cuadrado disminuido en una unidad’”.
En la tercera tarea se ofreció un conjunto de tres ecuaciones no lineales y se propuso discutir acerca de la naturaleza de sus soluciones. Las tres ecuaciones fueron:

Los datos que se analizaron se obtuvieron de la revisión de producciones escritas de los profesores, así como de algunas manifestaciones orales cuando las presentaron al grupo. Se eligieron aquellos episodios en los que se evidenciaron características sobre modos de pensamiento de los profesores. A continuación se presentan las situaciones con sus resultados y análisis respectivos.
A partir de los documentos y discusiones entre los profesores se pudo determinar un conjunto de características de los modos de pensamiento que evidenciaron los profesores al resolver las tres tareas.
En las respuestas se evidenció que, a pesar de mostrar la cónica de forma gráfica, los profesores desarrollaron la tarea 1 solo a partir de la expresión algebraica canónica de una parábola. Los participantes asumieron como ‘dado’ que la cónica correspondía a una ‘parábola’; ante ello, se preocuparon por realizar cálculos para determinar la expresión algebraica que describe al objeto ‘dado’. La asociación de la gráfica a una parábola sugiere que recurren a algunas características del modo de pensamiento sintético-geométrico; pero más allá de ello, su preocupación por los cálculos algebraicos sugiere que apelan con prioridad a características del modo de pensamiento analítico-aritmético.
Bien sea por la ‘certidumbre’ que ofrece el enunciado o por la confianza que se tiene en la representación gráfica, los participantes no cuestionaron la apariencia gráfica ni la relacionaron con la posibilidad de un tramo de una hipérbola o de una elipse. La ‘confianza’ en estos aspectos se manifestó también en la manera en que los profesores resolvieron la tarea. Todos los participantes supusieron al principio que al ser una ‘parábola’, a la gráfica le correspondía una de las formas de las ecuaciones de segundo grado. Algunos asumieron la expresión , otros , y uno de ellos asumió una expresión de la forma (ninguno anotó la expresión de en términos de para parábolas con eje horizontal). Una vez que plantearon la expresión algebraica, los profesores se concentraron en la correspondencia entre los datos aritméticos de la gráfica para plantear un sistema de ecuaciones y calcular los parámetros de la expresión general. En la Tabla No 1 se describen algunas características del modo de pensamiento que predominó en la resolución de la tarea.
Tabla 1
Modos de pensamiento presentes en la implementación de la tarea 1
Modo de pensamiento |
Característica |
Ejemplo |
analítico-aritmético |
El tipo de cónica se asume como “dada”. Ausencia de criterios geométricos, predominio de una interpretación como ‘función cuadrática’. Ausencia de criterios para validar la solución a la tarea.
|
Transcripción 1 (Mateo) “La ecuación general de la parábola es dependiendo si es completa o incompleta [refiriéndose a que tenga el término o ], entonces tomamos valores y los reemplazamos (...)”
|
El tipo de cónica se asume como “dada”. Se asume la definición canónica (analítica) de la cónica. Consideraciones de gráfica en correspondencia con la expresión algebraica. Ausencia de criterios para validar la solución a la tarea.
|
Transcripción 2 (Federico) “Como no nos dan el foco [refiriéndose a las coordenadas] necesitamos hallarlo utilizando la ecuación de la parábola es esta porque se abre hacia a la derecha. Después se reemplaza en la ecuación, se despeja , y se verifica para distintas coordenadas (Profesor Abel).
|
|
Fig.2
|
En los razonamientos de los profesores llama la atención que, en su totalidad, se privilegiaron los tratamientos algebraicos y se subordinaron otras formas de razonamiento. Si bien los profesores apelan a características estructurales de las ecuaciones de las cónicas (por ejemplo, la ecuación general de cualquier parábola), también es cierto que solo se usa como punto de partida para desarrollar procedimientos algebraicos y determinar una ecuación en particular. No se puede afirmar que hayan suficientes características de su pensamiento analítico-estructural porque no se presenta otro tipo de rasgos estructurales de la parábola (ej: relación entre las distancias de los puntos de la parábola a un punto, foco, y a una recta, directriz).
Esta interpretación se apoya en los elementos que los participantes consideraron como punto de partida para sus razonamientos. En todos los casos apareció el supuesto de que la cónica era una parábola y a partir de allí entraron en el ‘confort’ que los cálculos algebraicos ofrece. Este razonamiento es contrario a las indicaciones del enunciado. Su información de partida (hipótesis) es el conocimiento de que la gráfica corresponde a una cónica y a los datos que pudieran ser extraídos de la representación gráfica; de otro modo, la información que debía ser argumentada es el hecho de que la gráfica correspondiera a una parábola (tesis). En matemáticas, una práctica argumentativa (como lo es la demostración) parte de la información dada y desencadena un conjunto de inferencias que soportan el hecho (tesis); en el caso particular de la tarea, el razonamiento partió de la tesis (se supuso parábola) y se usaron los procedimientos algebraicos para determinar ‘la’ parábola que se creía pedida.
La presencia de este tipo de razonamientos puede corresponder a varios hechos. Entre ellos, se resaltan dos: el primero es la poca presencia de prácticas argumentativas en las instituciones escolares colombianas, el segundo es que la presencia de la forma en el gráfico cartesiano y de los datos numéricos podrían sugerir la necesidad de realizar, principalmente, cálculos algebraicos.
Para argumentar (no suponer) que la gráfica corresponde a una parábola se requiere del reconocimiento de cuáles son los aspectos conceptuales que caracterizan este tipo de cónicas. Ello implica también considerar que la mayor parte de la información que se proporcionó como punto de partida (hipótesis) se dio en un ambiente gráfico; es decir, gran parte de los argumentos deberían corresponder con características de un modo de pensamiento sintético-geométrico.
Otra posible dificultad para solucionar esta tarea mediante la interacción de los modos de pensamiento es que en educación básica, de forma particular, en geometría analítica, las cónicas están definidas por su lenguaje algebraico en términos de la ecuación canónica que, de alguna manera, ‘encapsula’ los aspectos que le dan origen. Es decir, mientras unos definen la parábola como la figura que queda después del trazo en un cono (definición geométrica), otros la definen en términos de las distancias a una directriz y un foco (también geométrica); después se usa esto para encontrar la ecuación canónica. Y cuando se encuentra, parece que lo demás se omite pues la ecuación canónica ‘absorbe’ lo anterior y se considera la única forma válida para demostrar en esta tarea.
Otros posibles caminos abordar la tarea podría incluir el uso de GeoGebra y la manipulación de las gráficas, por ejemplo:
Fig. 3
Animación en Geogebra 1

Parece que este tipo de interpretaciones geométricas no está presente cuando se da prelación al desarrollo de cálculos aritméticos y operaciones con expresiones algebraicas. Por lo tanto, es importante reformular los enunciados de las tareas escolares de forma que no se induzca a resolver las situaciones mediante un solo modo de pensamiento.
En la última solución geométrica propuesta se permite establecer una relación entre los distintos modos de pensamiento. Esta relación es mediada por un software que conjuga propiedades geométricas, algebraicas y conceptuales en un mismo objeto matemático. Aquí la visualización permite no limitarse a los cálculos algebraicos, desarrollar procesos cognitivos para centrar el interés en elementos conceptuales y rescatar el papel argumentativo de las gráficas para que se usen aspectos visuales y geométricos. Si bien cada una de estas acciones involucra características de los modos de pensamiento analítico y sintético, los aspectos analíticos se relacionan más con la experimentación y con una generalización de las características que con la presencia de cálculos de tipo algebraico.
En las evidencias presentadas en la Tabla No. 1 se infiere un uso de los procedimientos algebraicos como una manera de “descargar el razonamiento”, pues después de hacer los cálculos, ninguno de los participantes cuestionó sus resultados, ni propuso mecanismos de validación. Conforme Borba y Villarreal (2005) apuntan, la preferencia por el lenguaje simbólico como la manera de hacer demostraciones, hace que otras formas de argumentación (gráficas principalmente) no tengan presencia en la actividad matemática escolar. El no reconocimiento de los razonamientos fundamentados en gráficas y la visualización como formas de argumentación pudo influir para que no se manifestaran características de otros modos de pensamiento, como el sintético-geométrico o el analítico-estructural. De acuerdo con Beth y Piaget (1980), es importante considerar que en una demostración se pueden utilizar juicios de tipo sintético sin que se invalide la demostración, pues suponen principios lógicos y definiciones que no son exclusivos de las demostraciones analíticas, además de otras consideraciones intuitivas y geométricas.
La ausencia de acciones que se asocien a otros modos de pensamiento puede estar en relación directa con el hecho de que, al menos en Colombia, la geometría analítica, y en general el álgebra escolar, tiene un enfoque principalmente simbólico y procedimental (Agudelo-Valderrama, Clarke y Bishop, 2007). De alguna manera, este tipo de enfoques “encapsula” los aspectos que determinan los aspectos analíticos y sintéticos de las cónicas. Es decir, mientras unos definen la parábola como la figura que queda después del trazo en un cono (definición geométrica), otros la definen en términos de las distancias a una directriz y un foco (también geométrica); después se usa esto para encontrar la ecuación canónica (algebraica), que para los participantes de este estudio parece ser la principal, y quizás la única, manera de pensar la parábola.
Para construir representaciones del enunciado propuesto en la tarea 2 es posible usar “lenguajes” distintos que evidencian la utilización o no de los distintos modos de pensamiento. Sin embargo, parece imperar un tipo de representación que corresponde al modo de pensamiento analítico-aritmético, pues la totalidad de los participantes de este estudio respondieron a la tarea con la expresión algebraica .
Llama la atención que a pesar de haber discutido con anterioridad sobre otras formas de pensar y representar las ideas matemáticas, en ningún caso se utilizó una representación diferente a la algebraica. Una interpretación de este hecho es que, al igual que en la tarea 1, el enunciado y el contexto en el que se presenta de forma clásica ha servido como “entrenamiento” para que los estudiantes de 7° y 8° (12-14 años de edad) se vayan introduciendo en el álgebra y realicen cambios entre enunciados verbales y lenguaje algebraico. De otro modo, el enunciado lleva implícito una diferencia en el lenguaje, una cosa es “un número” y otra cosa es “cualquier número” o “todos los números”; en matemáticas estos términos pueden entenderse como sinónimos, pero en el lenguaje corriente sí tienen diferencia. En esta tarea, el enunciado mismo puede convertirse en obstáculo para promover otros modos de pensamiento.
En las matemáticas escolares se traducen enunciados verbales a expresiones algebraicas, sin embargo, es posible utilizar distintas formas de representación que ayuden al “tránsito” entre los modos de pensamiento. Por ejemplo, el tránsito de un lenguaje verbal a un lenguaje algebraico y, a su vez, a un lenguaje gráfico o funcional. De esta forma se evita la interpretación del número solo de manera discreta y se posibilita una interpretación como una cantidad continua, sin limitarlo solo al análisis analítico-aritmético dado por la expresión algebraica.
La siguiente gráfica muestra la altura desde el eje de las abscisas hasta un punto que puede desplazarse sobre la función f(x)=x2-1. En este caso, “el número” al que hace referencia el enunciado se asume como todo valor x del dominio de la función tal que “su cuadrado disminuido en una unidad” se interpreta geométricamente a partir de las coordenadas del punto para cualquier valor de .
Otro aspecto que puede evitar que se recurra a características de otros tipos de pensamiento, es que la función cuadrática se vincula en geometría de manera única con una parábola, lo cual muestra la separación entre los distintos modos de pensamiento. En la variación de sus coordenadas (x, x2-1) se puede reconocer también relaciones numéricas aplicables a esta tarea. Por lo tanto, es importante rescatar el papel argumentativo de las gráficas para que se usen aspectos visuales y geométricos en este tipo de situaciones y se vincule lo analítico y lo geométrico.
Fig. 4
Representación Gráfica

Como se muestra en la Fig. 4, en este caso se usan coordenadas de la función para definir la situación planteada, lo cual da cuenta de un tipo de pensamiento sintético-geométrico.
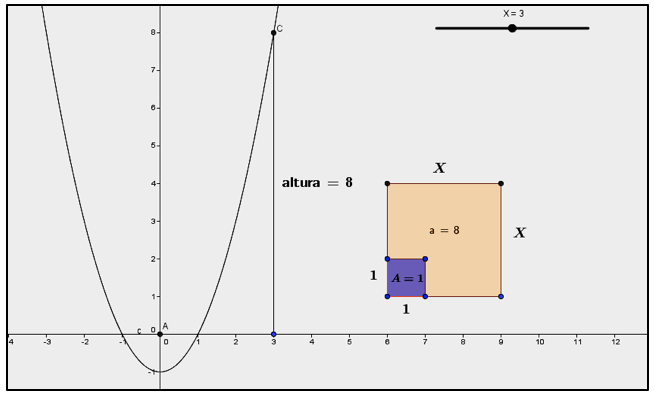
Otra representación, considerada también evidente, surge de la diferencia entre el área geométrica encerrada por un cuadrado de lado y un rectángulo cualquiera de una unidad cuadrada. En la Fig. 5 se observa que el punto puede desplazarse para tomar valores de , y la expresión “un número elevado al cuadrado disminuido en una unidad” corresponde al valor de la diferencia entre al área de cuadrado de lado y el área de una unidad cuadrada como se detalla en la figura.
Fig. 5
Representación Geométrica

Mediante la utilización de la tecnología, las diferentes representaciones permiten el “tránsito” entre los diferentes lenguajes (geométrico, algebraico). De esta manera, se promueve otras aproximaciones y comprensiones de objetos matemáticos desde distintos modos de pensamiento, y no como fragmentos desagregados sin ninguna interrelación.
La siguiente figura (Fig. 6) muestra que al variar un control (deslizador) se determina de manera simultánea una función y el área de la región correspondientes a la expresión: “un número elevado al cuadrado disminuido en una unidad”. Estas representaciones sugieren diferentes formas de interpretar los objetos matemáticos. Asimismo, posibilitan la discusión frente a la existencia o no de algunas de ellas en relación con el dominio de la variable x. Así, mientras existe una correspondencia directa entre el tramo positivo de la función y el cuadrado de la derecha, no ocurre lo mismo cuando la variable asume valores negativos pues no existe el cuadrado en mención. Todas estas conexiones entre representaciones e interpretaciones de los objetos matemáticos favorecen transiciones entre los diferentes modos de pensamiento, en particular entre el sintético, el analítico aritmético y el estructural.
Fig. 6
Animación en Geogebra 2
En las soluciones ofrecidas a esta tarea se pudieron identificar características del razonamiento de los participantes en relación con la resolución de ecuaciones.
Para el caso particular de la ecuación 5x=x^2+6, los participantes se limitaron a la aplicación de procedimientos, por ejemplo, la aplicación ‘fórmula’ general de la ecuación cuadrática 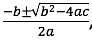 , la factorización y el tanteo.
, la factorización y el tanteo.
Para el caso de las ecuaciones y se evidenció una preocupación en los profesores al replicar los procedimientos aplicados en la ecuación i ya que los encontraron insuficientes para determinar las soluciones en estos dos nuevos casos. Parece que existe una tendencia por los cálculos aritméticos y los procedimientos algebraicos que no incluyen características de tipo estructural y conceptual cuando se consideran ecuaciones algebraicas
A continuación se ejemplifican otras formas de interpretar y solucionar las ecuaciones a partir de los modos de pensamiento.

Otra forma de solución que posibilita el uso de los modos de pensamiento sintético-geométrico y analítico estructural es la interpretación de la solución de una ecuación como la intersección de dos funciones. En el caso de la ecuación, 5x=x^2+6 se considera f(x)=x^2+6 y g(x)=5x. La solución a la ecuación corresponde a la intersección de las dos funciones puesto que la pregunta alrededor de la solución es ¿Para cuáles valores de las dos funciones son iguales? (ver Fig. 9).
Fig. 9
Representación cartesiana de la intersección de dos funciones.

Esta solución a través de dos funciones puede extenderse a las otras dos ecuaciones presentadas en la tarea 3. Sin embargo, los participantes solo hicieron manipulaciones algebraicas en cada una, por ejemplo: ‘transposición de términos’, aplicación de funciones inversas de las expresiones trigonométricas en las ecuaciones, entre otras.
Como ejemplo, se extiende la última solución presentada en la primera ecuación de la tarea 3. Esta muestra cómo, a través de características de los modos de pensamiento sintético-geométrico y analítico-estructural, se establecen relaciones y propiedades gráficas y algebraicas dadas con las expresiones y que generen discusiones alrededor de la solución a la pregunta. La siguiente ilustración corresponde a la situación, donde las gráficas de las funciones y se representan en el mismo plano.
Fig. 10
Representación gráfica de la solución de la ecuación

A partir del reconocimiento de características de las funciones involucradas, se puede determinar que la ecuación x^2+1=tan(x) tiene soluciones infinitas. El recurso visual se convierte en un insumo para reconocer que existen interceptos infinitos entre ambas funciones. A través del Software se puede describir el comportamiento (crecimiento y decrecimiento) de la función cuadrática acorde con los cambios de la variable x, y la recurrencia de las ‘ramas’ de la función tangente debidas su periodo. Este tipo de características ponen de relieve modos de pensamiento sintético pero ante todo, analítico-estructural, pues las funciones no se ven como ‘procesos’ de asignación de números sino como un ‘todo’ en el dominio de cada función. Al aplicar los mismos criterios a la tercera ecuación (sen(x)=4x^2+3), se obtienen argumentos visuales y analíticos para determinar que la ecuación no tiene solución en el sistema de los números reales.
Fig. 11
Representación gráfica de la solución de la ecuación
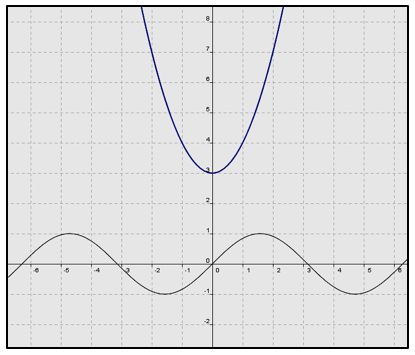
Para dar solución a las ecuaciones anteriores, los participantes trataron de realizar cálculos, procedimientos, factorizaciones y simplificaciones que desbordaron la aplicación de algoritmos básicos normalmente ‘memorizados’ para expresiones lineales. Esto se convierte en evidencia de la necesidad de no agotar las prácticas escolares en aspectos de tipo procedimental y aritmético, más allá de ello, se deben proporcionar experiencias para transcender hacia la construcción de otro tipo de estrategias visuales que promuevan características de los modos de pensamiento sintético y analítico-estructural.
Los resultados de este estudio convergen con los de Parraguez y Bozt (2012) y Agudelo-Valderrama et al. (2007), quienes señalan que en el trabajo algebraico en los cursos de Álgebra Lineal y en la Educación Básica predominan prácticas de tipo procedimental y la manipulación de símbolos. Si bien este tipo de prácticas son necesarias, deben superar la ejercitación memorística y algorítmica para relacionarse con los modos de pensamiento analítico. En palabras de Sierpinska (2000), al promover diferentes modos de pensamiento se evita el denominado ‘obstáculo del formalismo’, es decir, la manipulación de símbolos dentro del formalismo matemático sin un carácter conceptual que permita la compresión que subyace en ellos.
Los análisis de las respuestas de los participantes muestran que existen profesores para quienes el uso de gráficos y representaciones de tipo geométrico se ocultan ante la presencia de expresiones algebraicas. Frente a ello, se requiere promover experiencias a través de las cuales, tanto profesores como estudiantes se enfrenten a diversidad de tareas que promuevan diversidad de aprendizajes. En palabras de Watson y Sullivan (2008, citado en Lupiáñez, 2009), “diferentes tareas escolares proporcionan diferentes tipos de actividad matemática y las experiencias de los estudiantes con estas diferentes actividades indican distintos tipos de aprendizaje de las matemáticas (…)” (p. 61).
El estudio evidenció que la manipulación de procedimientos algebraicos se convierte en la principal característica de sus modos de pensar sobre los objetos matemáticos. Si bien esta característica es afín a un modo de pensamiento analítico-aritmético, también se requiere promover acciones para evidenciar características como las siguientes: las letras como variables (no solo un número fijo desconocido), ecuaciones como intersecciones entre funciones, áreas de figuras geometrías, entre otras.
Para estos profesores existe una fuerte tendencia a comprobar, resolver y demostrar enunciados de carácter matemático de forma analítica, posiblemente debido a los aspectos de la lógica formal que esta involucra, y se dejan de lado otras consideraciones intuitivas y geométricas que pueden ser válidas como métodos de demostración. Es importante considerar que aunque el modo de pensamiento sintético-geométrico sugiera elementos intuitivos en su desarrollo, no excluye aspectos teóricos y elementos del pensamiento analítico, pues las representaciones y construcciones geométricas están sustentadas en propiedades y definiciones.
Del estudio se derivan algunas implicaciones para los programas de formación inicial y continuada de profesores de matemáticas. En particular, promover el desarrollo de un conocimiento matemático que, articulado a su didáctica, permita crear diversidad de estrategias y heurísticas para afrontar una tarea; promover distintas interpretaciones de un objeto matemático; y diseñar tareas que promuevan interacciones entre los distintos modos de pensamiento matemático, entre ellos, los propuestos por Sierpinska (2000).
Agradecemos a la Vicerrectoría de Extensión y a la Dirección de Regionalización de la Universidad de Antioquia por el apoyo financiero del proyecto “Una mirada alternativa que favorece los distintos modos de pensamiento en la enseñanza de las matemáticas escolares” (2011), del cual se deriva este artículo. También agradecemos a los integrantes del grupo de Investigación MATHEMA-FIEM de la Universidad de Antioquia por los comentarios que hicieron a las versiones previas de este documento.
AGUDELO-VALDERRAMA, C., CLARKE, B., & BISHOP, A. J. (2007). Explanations of attitudes to change: Colombian mathematics teachers’ conceptions of the crucial determinants of their teaching practices of beginning algebra. Journal of Mathematics Teacher Education, 10(2), 69–93. https://doi.org/10.1007/s10857-007-9031-2
BETH, E. W., & PIAGET, J. (1980). Epistemología Matemática y Psicología. Barcelona, España: Editorial Crítica.
BONILLA, D. y PARRAGUEZ, M. (2013). La elipse desde la perspectiva de la teoría de los modos de pensamiento. En R. Flores (Ed.) Acta Latinoamericana de Matemática Educativa (pp. 617-624). México, DF: Comité Latinoamericano de Matemática Educativa.
BORBA, M. C., & VILLARREAL, M. E. (2005). Humans-with-media and the reorganization of mathematical thinking: Information and communication technologies, modeling, visualization and experimentation. New York: Springer
CANTORAL, R., & FARFÁN, R. M. (2003). Matemática Educativa: Una visión de su evolución. Educación y Pedagogía, XV (35), 203-214.
FLORES-MEDRANO, Eric; MONTES, Miguel A., CARRILLO, José, CONTRERAS, Luis C., MUÑOZ-CATALÁN, Mª Cinta, & LIÑÁN, Mª Mar. (2016). El Papel del MTSK como Modelo de Conocimiento del Profesor en las Interrelaciones entre los Espacios de Trabajo Matemático. Bolema: Boletim de Educação Matemática, 30(54), 204-221. Doi 10.1590/1980-4415v30n54a10
LLINARES, S. (2012). Formación de profesores de matemáticas. Caracterización y desarrollo de competencias docentes. Cuadernos de Investigación y Formación en Educación Matemática 7(10), 53-62.
LUPIÁÑEZ, J. L. (2009). Expectativas de aprendizaje y planificación curricular en un programa de formación de profesores de Matemáticas de secundaria. Granada, España: Editorial de la Universidad de Granada
NIESS, M. L., RONAU, R. N., SHAFER, K. G., DRISKELL, S. O., HARPER, S. R., JOHNSTON, C., . . . KERSAINT, G. (2009). Mathematics teacher TPACK standards and development model. Contemporary Issues in Technology and Teacher Education [Online serial]. Retrived from http://www.citejournal.org/vol9/iss1/mathematics/article1.cfm, 9(1)
PARRAGUEZ, M. y BOZT, J. (2012). Conexiones entre los conceptos de dependencia e independencia lineal de vectores y el de solución de sistemas de ecuaciones lineales en R² y R³ desde el punto de vista de los modos de pensamiento. Revista electrónica de investigación en educación en ciencias, 7(1), 49-72.
PINO-FAN, L. R., ASSIS, A., & CASTRO, W. F. (2015). Towards a Methodolgy for the Characterization of Teachers`Didactic-Mathematical Knowledge. Eurasia Journal of Mathematics, Science & Technology Education, 11(6), 1429-1456. Doi: 10.12973/eurasia.2015.1403a
PINO-FAN, L. R., & GODINO, J. (2015). Perspectiva ampliada del conocimiento didáctico-matemático del profesor. Paradigma, XXXVI(1), 87-109
ROWLAND, T. (2014). Frameworks for Conceptualizing Mathematics Teacher Knowledge. In S Lerman (Ed). Encyclopedia of Mathematics Education, p. 235-238
SFARD, A. (1991). On the dual nature of mathematical conceptions: Reflections on processes and objects as different sides of the same coin. Educational studies in mathematics, 22(1), 1-36. doi: 10.1007/BF00302715
SIERPINSKA, A. (2000) On Some Aspects of Students’ Thinking in Linear Algebra. In: J. L. Dorier (ed) On the Teaching of Linear Algebra (p. 209-246). Dordrecht: Springer
ROBUTTI, O. et al. (2016). ICME international survey on teachers working and learning through collaboration: June 2016, ZDM - Mathematics Education, 48(5), 651-690. Doi: 10.1007/s11858-016-0797-5
VILLA-OCHOA, J. A. (2015). Modelación matemática a partir de problemas de enunciados verbales: un estudio de caso con profesores de matemáticas. magis, Revista Internacional de Investigación en Educación, 8(16), 133-148. DOI: 10.11144/Javeriana.m8-16.mmpe
1. Magister en Enseñanza de las Ciencias Exactas y Naturales, Universidad Nacional de Colombia sede Medellín. Catedrático Universidad de Antioquia. Grupo de Investigación MATHEMA-FIEM. wbeimar.cifuentes@udea.edu.co
2. Doctor en Educación Matemática, Universidad de Antioquia. Docente Universidad de Antioquia. Coordinador grupo de Investigación MATHEMA-FIEM. jhony.villa@udea.edu.co