ISSN 0798 1015

Vol. 39 (Nº 08) Año 2018. Pág. 8

Análisis de Probabilidad de Devaluación de la Tasa de Cambio y Pronóstico de la Inflación en Colombia a través de un Modelo de Regresión Logística y Serie de Tiempo Estacionaria 2005 - 2016

Analysis of the Probability of Exchange Rate Depreciation and Inflation Forecast in Colombia by a Logistic Regression Model and Stationary Time Series 2005 - 2016

Jose J. GONZALEZ 1; Nidia P. AMADO 2; Ana M. SERRANO 3

Recibido: 19/10/2017 • Aprobado: 22/11/2017

Contenido

1. Introducción

2. Marco teorico

3. Metodologia

4. Resultados

5. Conclusiones

Referencias

1. Introducción

El sistema económico mundial es visto como una red de hilos entrelazados que, sin generar nudos, interactúan para buscar el equilibrio y el sostenimiento de las condiciones de calidad de vida de la sociedad que depende de ellos. Cada hilo podría definirse como una variable que interactúa con otras que, como ella, en algunos casos es explicada y en otros es explicativa. Siguiendo el sentido figurado, podríamos decir que cuando un hilo se tensiona, flexibiliza, alarga, acorta, etc, puede generar efectos en los demás, modificando el equilibrio del sistema del que hace parte. Existen numerosos análisis desde el punto de vista econométrico para determinar los efectos que puede generar el cambio de una variable sobre otras y, para ello, se recurre a modelos matemáticos que en la actualidad se encuentran como herramientas de software.

En consecuencia, cuando se habla de un aumento generalizado del nivel de precios de una economía, es decir, de la Inflación, se sospecha que hay diferentes efectos no sólo en el nivel de precios, sino en otras variables como devaluación, ingreso, crecimiento del PIB, tipo de cambio, importaciones y exportaciones, entre otras. Por lo tanto, cuando hay inflación, no hay incentivación de las actividades productivas, puesto que se genera incertidumbre sobre los futuros precios. No obstante, cuando se habla de efecto transmisión, se hace referencia al porcentaje en que los cambios se reflejan en las variaciones de los precios de importación de un país. Por ende, tanto el impacto sobre los precios de exportación, como la transmisión periódica de los precios de importación a las variaciones de los precios internos (IPP-IPC) son importantes para comprender el efecto del tipo de cambio sobre la inflación.(Hernández et al., 2009)

Este articulo busca analizar los efectos que dichas variables ejercen sobre la devaluación y, específicamente, mostrar el traspaso del tipo de cambio a la inflación y predecir la probabilidad de devaluación o revaluación del tipo de cambio, a través de un modelo econométrico LOGIT en el periodo 2005 – 2015. Finalmente, se hace un pronóstico de la inflación trimestral para 2016, para lo cual se utilizó el modelo SARIMA de una serie de tiempo estacionaria en media y estacionaria en varianza.

2. Marco teorico  

En este marco teórico se describen temas como la inflación, el efecto transmisión, los modelos causales, los modelos LOGIT, los modelos de serie temporales, los modelos SARIMA, y los pronósticos de inflación.

La inflación

La inflación es uno de los temas más preocupantes en la economía de los países, teniendo en cuenta que su aumento o disminución genera graves consecuencias, a tal punto de llevar a la ruina de las naciones. Para entender mejor los efectos tanto positivos como negativos del tema en estudio es conveniente partir del concepto.

Principales conceptos de Inflación

La inflación es estudiada principalmente desde el área de economía; autores como Garay y Salazar (2016) la conceptualizan como “el incremento sostenido de los precios de los bienes y servicios de una economía durante un período” (p. 21). A partir de esta definición, puede deducirse que, al aumentar los precios de bienes y servicios, el costo de vida será más elevado. Por tal razón, los gobiernos deben mantener políticas que permitan tener un control sobre los precios.

Para respaldar lo antes mencionado Cárdenas y Vallejo (2013) Indican que: 

Cuando se habla de inflación, se hace referencia a la pérdida del poder adquisitivo, es decir, a la disminución del ingreso real de los trabajadores y, por ende, al deterioro de la calidad de vida de la población. En otras palabras, si la inflación aumenta, la cantidad de bienes y servicios a los que pueden acceder los agentes económicos es menor, si no hay un aumento en el salario nominal. (p. 35).

Puede concluirse que la inflación es el aumento de los precios de una canasta de productos y/o servicios de gran importancia en la economía de un país (Catacora, 2000). De esta manera, la inflación es relacionada por los consumidores con en el índice de precios del consumidor (IPC), es decir, el aumento de los precios en los productos de la canasta familiar.

Por otra parte, para Fernández (citado por Uzcátegui, De La Hoz, Borges y Velazco (2008): “la inflación puede ser considerada como una enfermedad de la economía cuya causa principal es la existencia de mucho circulante en poder del público y poca producción de bienes y servicios” (p. 559). Por lo tanto, la inflación no solo es producto del alza de precios en los productos o servicios, ésta también se debe a una baja producción en donde los consumidores cuentan con el dinero para adquirir los productos, pero los bienes están escasos.

Efectos adversos de la inflación

Mantener una estabilidad de precios se ha convertido en un reto para los encargados de desarrollar y evaluar las políticas monetarias en cada país, ya que la estabilidad es sinónimo de crecimiento y poder de compra. Pero si estas políticas no son controladas de manera permanente, de acuerdo con Brum, Román y Willebald (2016), estos efectos pueden clasificarse en seis categorías:

Costos de búsqueda asociados con los incentivos de los agentes de no mantener dinero en efectivo y buscar alternativas de colocación que paguen interés o signifiquen un resguardo ante la inflación. Los costos de menú, relacionados con todos los inconvenientes de los empresarios de modificar frecuentemente los precios de lista en lugar de aplicar atención y recursos en actividades más productivas. Cambios no intencionados en la estructura impositiva con consecuencias adversas sobre la recaudación fiscal real (tipo “efecto Olivera-Tanzi”). Los efectos redistributivos de la riqueza asociados con las diferentes posibilidades de cobertura que muestran los distintos segmentos sociales. La incertidumbre derivada de la inflación puede afectar la inversión y el consumo ante las dificultades de predecir ganancias e ingresos futuros; y, finalmente, una elevada variabilidad de los precios relativos puede incidir sobre la competitividad de la economía y afectar su frente externo y nivel de actividad (p. 66).

Tipos de inflación

Los diversos tipos de inflación pueden clasificarse desde dos puntos de vista, por una parte, desde los niveles de gravedad y, por otra, desde la identificación de los elementos más importantes y expuestos por los Neokeynesianos.

Tipos de inflación de acuerdo a los niveles de gravedad

Desde este enfoque existen tres tipos de inflación categorizados por García (2016) de la siguiente manera:

Inflación moderada: se caracteriza por una lenta y predecible alza de los precios. Sus tasas anuales son de un digito. Cuando los precios son relativamente estables, el público confía en el dinero. Inflación Galopante: la inflación es de dos o tres dígitos y oscila entre 20%, 100% o 200% al año… el dinero pierde valor rápidamente y los consumidores no tienen más la cantidad de dinero mínima para realizar las transacciones diarias. Hiperinflación: No se puede decir nada bueno cuando en una economía los precios suben en un millón por ciento al año, todo escasea menos el dinero, los precios son caóticos y la producción esta desorganizada (p. 8-10).

Tipos de inflación desde el punto de vista Neokeynesiano

Los autores antes mencionados resaltan que los neokeynesianos reconocen los dos tipos de inflación según los elementos más importantes:

La inflación tipo demand-pull ocurre cuando el exceso de demanda agregada supera a la oferta disponible. Esta brecha del producto (output gap) puede resultar por un aumento en los gastos del gobierno o del sector privado, incrementos en la demanda internacional, o la expansión en la oferta monetaria. (Brum, Román, y Willebald 2016, p. 67).

Este tipo de inflación se presenta básicamente porque hay más compradores que artículos producidos y, como se mencionaba antes, el dinero circulante es mayor y no existen beneficios para las personas que hacen parte de esa economía.

En el otro extremo de la economía se presenta la caída inesperada de la inflación, la cual generalmente ocurre cuando hay aumentos en el costo de las materias primas y los consumidores no cuentan con los recursos para pagarlos. A este tipo de inflación se le conoce como inflación tipo aumento de costos, la cual refiere a la inflación asociada con choques de oferta que implican caídas repentinas de ésta, ante aumentos del precio/costo de los bienes/productos y la inexistencia de alternativas en el corto plazo.

Estar preparados para mantener estabilidad en los precios requiere establecer una política monetaria sólida que permita un adecuado control del entorno y de cada uno de los factores que pueden incidir en el alza de los precios.

Diferencia entre inflación objetivo y objetivos de inflación

La base de estos términos, tanto en estructura como en la forma en que se deben diseñar las políticas para lograrlos, es diferente puesto que por una parte Ampudia, citada por Alvarez (2017), destaca que en “la inflación objetivo (Inflation Targeting) su propósito es explícito y puntual mediante un rango”, es decir, busca contribuir a que los precios permanezcan estables mediante objetivos jerarquizados que contribuyan a su cumplimiento.

En cuanto a los objetivos de inflación (Inflation Targets) el autor antes citado considera que “el objetivo es implícito y permite un margen de acción y discrecionalidad en la política monetaria” (p. 22). Por lo tanto, se actúa en favor del crecimiento monetario del país por medio de la generación de empleo y oportunidades para su comunidad, de tal manera que sean los individuos quienes generen los recursos económicos.

Teoría Estructuralista de la Inflación

La inflación se ha atribuido al desarrollo excesivo, en otras palabras, a que circula demasiado dinero, pero la teoría estructuralista, explicada por el mexicano Juan Noyola Vásquez, citado por Flores, Martínez y Padilla (2006) expone que:

La inflación no está causada por un “exceso de crecimiento”, sino precisamente por su insuficiencia. En algunos sectores económicos la demanda es muy inelástica, pero el insuficiente desarrollo y el pequeño tamaño de algunas economías que impiden que esa demanda sea satisfecha internamente, por lo que aparece una fuerte dependencia del exterior (p. 227).

De acuerdo con esta teoría, no es el exceso de dinero o el crecimiento de un país el que genera la inflación, por el contrario, se considera que la inflación se debe a la demanda interna insatisfecha, por lo tanto, es necesario recurrir al exterior para adquirir los productos o materias primas que se requieren. Por ende, se elevan los costos de producción y se genera un incremento en el costo de vida de la población.

Por otra parte, el principal exponente de esta teoría reconoce que los sistemas de propiedad y producción agraria están desfasados, a tal punto que presentan un estrangulamiento por la rigidez de la oferta.  Flores, Martínez y Padilla (2006). A partir de esta teoría, se deduce que la inflación se presenta porque no existe coherencia entre las necesidades de los productores agrícolas y las políticas desarrolladas por el gobierno, ya que las tasas de interés para este sector son altas, y las políticas monetarias no garantizan una estabilidad de precios, por lo tanto, el desequilibrio entre los campesinos y el gobierno es evidente.

Los exponentes de la teoría estructuralista proponen que “para corregir la inflación, no hay que atacar los síntomas, el aumento de la circulación monetaria, sino atacar la raíz del mal y corregir los desequilibrios entre grupos y clases sociales y entre las ciudades y el campo” (p. 228).

Inflación Importada

Como lo establece la teoría estructuralista de la inflación, cuando un país tiene sus políticas económicas que no favorecen su parte interna, el tratar de establecer acuerdo con otros países para importar aquellos productos que se consideran escasos afecta aún más a la economía del país. A partir del desequilibrio financiero que causa la situación expuesta anteriormente surge el concepto de Inflación Importada, definida por Rodríguez (2009) como aquella inflación en la cual:

El aumento de precios de bienes y servicios está ligado a los impactos que se generan en la inflación local, resultado de un cambio de la inflación extranjera… a este fenómeno se le considera una de las causas de inestabilidad financiera en economías pequeñas y abiertas (p. 81).

Por su parte, The Oxford Dictionary of Economics s.f., (citado por Rodríguez 2009) define la inflación importada como 

La inflación debido a los aumentos en los precios de las importaciones, los aumentos en los precios en los productos finales importados afectan directamente a los gastos basados en la medida de la inflación. Por ejemplo, los aumentos en los precios de los combustibles, los materiales y componentes de aumento en los costos de producción dan lugar a aumentos en los bienes de producción nacional (p. 82).

2.1. Efecto transmisión

La definición de efecto transmisión de la tasa de cambio según (Devereux y Engel, 2002) es el porcentaje de cambio del precio de las importaciones en moneda local como resultado de una variación de uno por ciento en la tasa de cambio nominal entre países exportadores e importadores. En una economía pequeña y abierta donde los agentes se comportan como tomadores de precios, se espera que el efecto transmisión sea completo, esto quiere decir que se cumple la ley de un solo precio y que, una depreciación (apreciación) implicará un aumento (disminución) de los precios domésticos en la misma magnitud para reestablecer, a largo plazo, la razón de precios relativos. Asimismo, en el estudio realizado por (Romero, 2012) el concepto del efecto transmisión es el de las variaciones que tienen el tipo de cambio sobre la inflación interna.

En mercados perfectamente integrados se espera que los precios de los bienes y servicios con las mismas características sean los mismos en cualquier parte del mundo, es decir, que se cumpla la ley del precio único. La versión absoluta de esta ley es la siguiente:

P I = P i ∗

Donde Pi es el precio del bien i en moneda doméstica, P*i es el precio del bien en moneda extranjera y E es la tasa de cambio nominal. Si en un mercado se cumple la ley del precio único también debe cumplirse la paridad del poder adquisitivo (PPA), la cual afirma que los niveles de precios de todos los países son iguales cuando se expresan en términos de la misma moneda. La existencia de costos de transporte, barreras comerciales y de bienes no transables hacen que la ley del precio único no se cumpla en la práctica.

Pronósticos

Ya que la inflación es un factor determinante del sistema de precios, requiere que se disponga de una visión anticipada del indicador, es decir, contar con proyecciones realizadas mediante la utilización de métodos confiables, pues esto permitirá establecer políticas anti-inflacionarias apropiadas, para tratar de alcanzar una estabilidad económica (Moreno, Rivas y Villarreal, 2014).

Dada la incertidumbre del sistema económico, surge la necesidad de hacer pronósticos que se plantean bajo criterios de tiempo y contexto. Según (Kennedy, 1985) existen dos tipos de predicciones: (1) Predicción dentro de la muestra: tiene que ver con la capacidad del modelo para describir la realidad y para predecir dentro del intervalo muestral, considera todo el intervalo muestral y para las proyecciones únicamente se utiliza una parte de dicho intervalo muestral. (2) Predicción fuera de la muestra: Se relaciona con la capacidad del modelo para describir la realidad y para predecir fuera del intervalo muestral el comportamiento de la variable endógena.

Horizonte de preidicción: Se considera que mientras mayor sea el horizonte de predicción, existe mayor probabilidad de cambio en los patrones o relaciones porque el comportamiento o actitudes de las personas pueden variar y porque pueden producirse cambios fundamentales en el contexto, por ejemplo, cambios tecnológicos. Es por ello que las predicciones se basan en análisis en escenarios de corto, mediano y largo plazo.

Las predicciones de corto plazo son predicciones a un plazo menor o igual a tres meses, en este caso se recomienda considerar los cambios en los patrones y relaciones económicas que pueden producirse y de hecho se producen. Sin embargo, debido a los cambios, la mayoría de los fenómenos económicos no son inmediatos, éstos no influyen en gran medida en las proyecciones de corto plazo. Estas predicciones son más precisas y confiables, ya que reducen los errores de predicción de los modelos de mediano plazo y permiten asesorar en forma más adecuada la toma de decisiones de política.

Las predicciones de mediano plazo son las predicciones que cubren un periodo superior a tres meses, pero inferior a los dos años. Las predicciones de mediano plazo no suelen ser muy confiables debido a la dificultad de predecir los puntos de cambio en los ciclos económicos, las recesiones y las épocas de expansión. En el campo empresarial, estas predicciones son útiles para la toma de decisiones, por ejemplo: presupuestos, asignación de recursos, etc. Por lo tanto, deben tenerse en cuenta sus limitaciones para predecir recesiones y booms en la economía que sean capaces de ajustarse a los cambios cíclicos.

Las predicciones de largo plazo son aquellas que cubren periodos iguales o superiores a los dos años. Estas predicciones suelen ser poco confiables, pues no puede determinarse el error de predicción, ya que con el paso del tiempo pueden producirse cambios imprevistos en la tendencia, discontinuidad, nuevos acontecimientos, etc.

Uno de los objetivos principales de la política económica en temas de inflación, es lograr tener un pronóstico acertado de ésta para tomar decisiones anticipadas en los frecuentes escenarios de incertidumbre. Es así que se hace uso de modelos econométricos en el estudio de la inflación, con el fin de usar el modelo identificado y estimado para realizar pronósticos.

De acuerdo con la literatura, existen dos aproximaciones de modelos utilizados como herramienta de pronóstico de la inflación: (i) modelos econométricos estructurales o "causales" y, (ii) modelos de series de tiempo (Granger & Newbold, 1977).

2.2. Modelos causales

Como lo menciona (Ruiz, 2000), los modelos de ecuaciones estructurales o causales, son una familia de modelos estadísticos multivariantes que permiten estimar el efecto y las relaciones entre múltiples variables. Los modelos de ecuaciones estructurales nacieron de la necesidad de dotar de mayor flexibilidad a los modelos de regresión. Son menos restrictivos que los modelos de regresión por el hecho de permitir errores de medida tanto en las variables criterio (dependientes), como en las variables predictoras (independientes).

Estos modelos intentan identificar las relaciones que causaron los datos históricos observados, luego se puede predecir aplicando estas relaciones en el futuro.

La ventaja del modelo causal de predicción es que puede desarrollarse una serie de predicciones correspondientes a una serie de valores para las diferentes variables explicativas. Sin embargo, requieren información de variables, por lo que son más sensibles a los cambios en las relaciones subyacentes y dependen de estimación de los valores futuros de los factores para predecir (Ruiz, Pardo, & San Martín, 2009).

Asimismo, los modelos de ecuaciones estructurales se basan en las correlaciones existentes entre las variables medidas en una muestra de sujetos de manera transversal. Por tanto, para realizar las estimaciones, basta con medir a un conjunto de sujetos en un momento dado. Este hecho hace especialmente atractivos estos modelos. Ahora bien, hay que tener en cuenta que las variables deben permitir el cálculo de las correlaciones y por ello deben ser variables cuantitativas, preferentemente continuas. Los puntos fuertes de estos modelos son: haber desarrollado unas convenciones que permiten su representación gráfica, la posibilidad de hipotetizar efectos causales entre las variables, permitir la concatenación de efectos entre variables y permitir relaciones recíprocas entre variables (Ruiz, 2000).

2.3. Modelos LOGIT

Este modelo permite, además de obtener estimaciones de la probabilidad de un suceso, identificar los factores de riesgo que determinan dichas probabilidades, así como la influencia o peso relativo que éstos tienen sobre las mismas.

Este tipo de modelo arroja como resultado un índice, cuyos determinantes son conocidos, el cual permite efectuar ordenaciones, las cuales al realizarse, posibilitan, con algún método de estratificación, generar clasificaciones en las que se le asocia a cada elemento una calificación. Existen muchos criterios para llevar a cabo la asociación índice - calificación, muchos de ellos con base en índices de muestreo, donde el criterio es puramente estadístico. Otros criterios podrían considerarse como subjetivos.

Para el caso más sencillo, el de una única variable explicativa, se trata de encontrar la relación que existe entre la variable explicativa y la endógena. Las posibilidades que se plantean son:

Que la función que relaciona ambas variables sea una función lineal, caso en el cual se tiene, lo que se ha denominado, el modelo lineal de probabilidad. Este asume que la relación entre las variables explicativas y la variable explicada tiene un comportamiento lineal, suposición que en muchos casos no se da, dando esta situación origen a los modelos de regresión no lineales, dentro de los cuales se encuentra ubicado el modelo Logit (Cramer, 1968).

La modelización Logit es similar a la regresión tradicional salvo que utiliza como función de estimación la función logística en vez de la lineal. Con la modelización Logit, el resultado del modelo es la estimación de la probabilidad de que un nuevo individuo pertenezca a un grupo o a otro, mientras que por otro lado, al tratarse de un análisis de regresión, también permite identificar las variables más importantes que explican las diferencias entre grupos.

Existen distintos tipos de modelos Logit en función de las características que presenten las alternativas que definen a la variable endógena. Esta variable permite medir el número de grupos existentes en el análisis, según (Cramer, 1968), los modelos Logit se pueden clasificar así :

1) Logit dicotómico: se utiliza cuando el número de alternativas son dos y excluyentes entre sí.

2) Logit de respuesta múltiple: se utiliza cuando el número de alternativas a modelizar es superior a dos.

3) Logit con datos no ordenados: se utiliza cuando las alternativas que presenta la variable endógena no indican ningún orden.

4) Logit multinomial: se utiliza cuando los regresores del modelo hacen referencia a las observaciones muestrales, por lo que varían entre observaciones pero no entre alternativas.

5) Logit condicional: se utiliza cuando los regresores del modelo hacen referencia a las alternativas, por lo que sus valores varían entre alternativas pudiendo hacerlo o no entre observaciones.

6) Logit con datos ordenados: se utiliza cuando las alternativas de la variable endógena representan un orden entre ellas.

Modelo Logit Dicotómico

Este modelo presenta las siguientes características: Variable endógena binaria, identifica la pertenencia del individuo a una de dos posibles categorías, identificando con el número 1 si el individuo pertenece a la característica de interés cuya probabilidad se estimará en el modelo. Se identifica con 0 al elemento que no posee la característica de interés, cuya probabilidad también se estima con el modelo (Wooldridge, 2002).

Variables exógenas, son las variables que permiten discriminar entre los grupos y que determinan la pertenencia de un elemento a un grupo u otro. Pueden estar medidas en escala nominal, ordinal, de intervalo o de razón.

Resultado del análisis, el resultado del análisis es un vector de parámetros con valores numéricos, que son los coeficientes para cada uno de las variables explicativas que hacen parte definitiva del modelo. La importancia radica en que a cada valor del vector de parámetros le corresponde una variable explicativa, al tenerse en cuenta todas en conjunto y dar valores a cada una de las variables independientes contenidas en el modelo definitivo, se obtiene el valor de la probabilidad de que un individuo posea la característica de interés estudiada en el modelo.

Modelos de Series Temporales

En este tipo de modelos como lo afirma Harvey (1990) en el análisis de series temporales 4, se hacen predicciones para valores futuros de una o más variables; pero para ello se usa únicamente la información contenida en los valores pasados de la serie, la misma que mide la evolución de las variables estudiadas. Es decir, se identifica los patrones históricos y después, bajo el supuesto de que se mantienen constantes en el futuro, predecir utilizando la metodología más adecuada.

Un modelo de series temporales puro, puede no ser estable a lo largo del tiempo; y, como consecuencia, las predicciones obtenidas pueden ser imprecisas.

Los modelos de series temporales pueden ser: Univariantes y Multivariantes (Granger y Newbold, 1977): 

Univariantes.- Analiza una serie temporal en función de su propio pasado, como es el caso de los modelos SARIMA 5.

Multivariante.- Analiza varias series temporales a la vez; es decir se cuenta con diversas variables, que pueden ser endógenas como es el caso de los modelos VAR 6 y variables exógenas cuando son modelos VARX 7.

2.4. Modelos SARIMA

Box y Jenkins (1970) ofrecen la manera de lograr pronósticos a través de la construcción, identificación y predicción de un proceso Autorregresivo de Media Móvil Estacional, SARIMA 8. De acuerdo a esta teoría, el análisis de series de tiempo implica las siguientes etapas: (i) Identificación, (ii) Estimación, (iii) Verificación y, (iv) Pronóstico (Predicción). Si la serie es débilmente estacionaria, se procede de inmediato con la etapa (i); caso contrario, la serie debe ser "pre-procesada" a fin de ser transformada en realizaciones estacionarias. Asumiendo que se cuenta con series estacionarias, la identificación tiene por objeto determinar el tipo de modelo a aplicar (AR, MA o ARMA) y el orden de los parámetros "p" y "q" 9.

Este modelo permite describir un valor como una función lineal de datos anteriores debidos al azar, e incluso puede utilizar componentes cíclicos o estacionales. Es decir, que debe contener una base completa de datos históricos estructurados para los pronósticos. Usualmente para la aplicación del modelo se utiliza el modelo Box y Jenkins, (1970) que se resume en los siguientes pasos: 1) identificar el posible modelo ARIMA, lo que requiere decidir que transformaciones aplicar para convertir la serie observada en una serie estacionaria, seguido de la determinación de una serie ARMA para la serie estacionaria, es decir los órdenes p y q de su estructura autorregresiva y media móvil. 2) seleccionar provisionalmente un modelo para la serie estacionaria. Estimación de los parámetros AR y MA del modelo, lo cual se realiza por máxima verosimilitud y se obtienen sus errores estándar y los residuos del modelo. 3) realizar el diagnóstico, donde se comprueba que los residuos no tienen estructura de dependencia y siguen un proceso de ruido blanco. Si los residuos muestran estructura se modifica el modelo para incorporarla y se repiten las etapas anteriores hasta obtener el modelo adecuado. 4) predecir con base en el modelo adecuado.

Para el análisis de datos se recomienda seguir los siguientes pasos: 1) Recolección de datos: En número debe ser consistente acorde a los ciclos seleccionados.  2) Representación gráfica: Permite observar la tendencia y marcación de la estacionalidad. 3) Transformación de la tendencia: En caso de que a primera vista no se evidencien claras marcaciones de estacionalidad, se podrían utilizar series corregidas de primeras diferencias, segundas diferencias o logarítmicas. 4) Identificación del modelo: Se aplican los conceptos AR, MA, sobre análisis de pruebas iterativas. 5) Estimación de los coeficientes del modelo: Debido a que se realizan pruebas iterativas. 6) Contraste de validez del modelo: Con base en los resultados estadísticos. 7) Análisis detallado de errores. 8) Selección definitiva del modelo: Seleccionar del modelo más adecuado. 9) Predicción: De acuerdo a la formula seleccionada.

Análisis lógico del Modelo AR

Un modelo autorregresivo AR describe una clase particular de proceso en las observaciones en un momento dado son predecibles a partir de las observaciones previas del proceso más un término de error.

El caso más simple es ARIMA (1,0,0) o RA (1) o de primer orden cuya expresión matemática es:

La metodología afirma, que podría existir un componente estacional en el modelo analizado ARIMA 10 por lo que se deben revisar los rezagos en los que frecuentemente hay estacionalidad y por lo tanto se deberá usar en la estimación del modelo ya sea un término SAR o un término SMA (P o Q respectivamente) según sea el caso.

La estacionalidad Autorregresiva SAR se observa en la función de autocorrelación simple, mientras que la estacionalidad en media móvil SMA se observa en la función de autocorrelación parcial. La presencia de un componente estacional ya sea en el componente autorregresivo o en el componente de media móvil hace que el modelo estimado se convierta en un modelo SARIMA (P, D, Q) 11.

2.5. Literatura sobre pronósticos de inflación

A continuación se presentan algunos trabajos realizados en diferentes países acerca de pronósticos de inflación, utilizando modelos econométricos causales y de series de tiempo.

Stock y Watson (2008) realizaron estudios con base en la curva de Phillips, entendida como modelos para predecir la inflación con base en una o más variables de actividad, se definió en el resultado que tendrían capacidad predictiva sólo en algunos periodos específicos, mientras que en otros esta capacidad predictiva desaparecería.

Por otro lado, Nadal (2001) estima una curva de Phillips con parámetros variables y encuentra, en un análisis dentro de muestra, que todos los coeficientes son significativos, puesto que muestra una trayectoria persistente que abarca valores positivos, y finalmente se acerca a cero, indicando que si la brecha de producto tuvo alguna vez importancia en predecir la inflación, esta se fue perdiendo hacia el final del periodo muestral.

Aguirre y Céspedes (2004) muestran que una curva de Phillips aumentada con factores dinámicos de acuerdo a la metodología fuera de muestra, mejoran la capacidad predictiva de una curva de Phillips tradicional para horizontes de 6, 9 y 12 meses. Este modelo aumentado supera un benchmark univariado en horizontes de 9 y 12 meses.

Finalmente un estudio realizado por Fuentes, Greding y Larraín (2008), evalúan la capacidad predictiva fuera de muestra de varias curvas de Phillips lo que llaman ejercicio predictivo “casi” en tiempo real, encontrando entonces que las medidas de brecha de producto tienen capacidad predictiva para la inflación en horizontes de 3 a 4 meses.

En México Espasa, Molina y Ortega (1984), realizan un análisis econométrico sobre una desagregación de los indicadores que son aplicados a modelos univariantes y también a modelos de transferencia, los resultados fueron la obtención de proyecciones de inflación de corto plazo para México.

Así mismo, para Perú, Barrera (2007) utiliza modelos VAR tradicionales y sparseVAR para elaborar proyecciones desagregadas de la variación del IPC, en el cual muestra que casi todas las desagregaciones planteadas en su trabajo se ajustan con mayor precisión a la hora de proyectar el agregado IPC en el corto plazo; para un periodo de 1-6 meses.

En Uruguay, Garda et al., (2004) realizan pronósticos de la inflación utilizando modelos de series de tiempo. Utilizan un análisis por componentes, así mismo Conrado, Cuitiño, Mourelle y Vicente (2012) presentan para Uruguay  un conjunto de modelos multivariados de función de transferencia mediante los cuales se proyectan diferentes componentes del IPC, el resultado evidencia que la agregación de estos componentes genera proyecciones del IPC con buen poder predictivo para plazos cortos e intermedios, y que estos modelos podrían ayudar a superar algunas limitaciones de los  modelos univariados, usados actualmente para el corto plazo, permitir incorporar información externa a la propia serie de tiempo del IPC.

En Venezuela, Barráez y Perdomo (2010) realizan una estimación mediante métodos bayesianos un VAR y un modelo estocástico de equilibrio general dinámico (MEEGD), en el que demuestran que los MEEGD no son tan predictivos en comparación con los modelos VAR; razón por la cual los bancos centrales y los diseñadores de políticas públicas utilizan los modelos VAR, gracias a su buen desempeño predictivo.

Para Ecuador, Gachet, Maoldonado, & Pérez, 2008) hacen un estudio para el banco central, acerca de la aplicación de modelos vectoriales autorregresivos para proyectar la inflación, éste sostiene que un modelo VAR es uno de los modelos más flexibles y eficaces para predecir la inflación, puesto que permite analizar grupos de variables y cuantificar la interrelación entre ellas sin tomar en cuenta alguna estructura económica.

Por su parte en Colombia, se han realizado estudios de pronóstico en el Banco de la república como el de González (2008), en el que se analiza empíricamente si los pronósticos para la inflación agregada de alimentos pueden ser mejorados, en términos de reducir el error de pronóstico. Se evalúan y comparan modelos tanto univariados como multivariados según su capacidad de pronóstico. Los resultados muestran, que los pronósticos construidos a partir de pronósticos de subgrupos de alimentos generados por modelos multivariados producen menor error de pronóstico que los generados por un modelo univariado.

Así mismo Rodríguez y Siado (2003), realizan un ejercicio de pronóstico no paramétrico para la inflación colombiana mensual, usan estimación Kernel para la media condicional de los cambios de la inflación dada su propia historia. Los resultados de pronóstico se comparan con un modelo ARIMA estacional y un modelo tipo STAR, con el cual encuentran que, excepto para el pronóstico un mes adelante, el pronóstico no parametrito supera a las otras dos metodologías que le compiten; además, concluyen que de los tres modelos considerados el no paramétrico es el único pronóstico que estadísticamente mejora al pronóstico que se hace con un modelo de caminata aleatoria.

Por otra parte Castaño y Melo (s. f), realizan un análisis de  métodos de combinación de pronósticos de diferentes modelos econométricos, aplicado a la inflación colombiana, con el cual se pretende encontrar una combinación lineal de pronósticos de diferentes modelos que produzca una predicción mejorada en términos de precisión. Con la simulación realizada en dos ejercicios, los resultados muestran que bajo técnicas adecuadas de combinación de pronósticos es posible obtener alrededor de un 50% y 35% de ganancia en precisión con respecto a los modelos individuales para horizontes de uno y cuatro trimestres, respectivamente.

3. Metodologia

Cada uno de los modelos utilizados explora un conjunto distinto de información y tiene una capacidad probabilística y predictiva variable, con la cual, el análisis de los resultados que arrojan estos modelos, en conjunto con los demás elementos de juicio con que cuenta el Banco de la República, permite enriquecer el proceso de toma de decisiones.

En primer lugar, se utiliza la metodología de estimación de modelo Logit para variables dicótomas, con el fin de determinar la probabilidad de devaluación del tipo de cambio. Esta metodología se caracteriza por una Variable endógena binaria: DEV, en este caso si la devaluación es negativa recibe el valor 0 y si es positiva recibe el valor 1; además cuenta con variables exógenas: PIB, MS, XS, GAP, TIINT y Prime Rate. Luego de estimar el modelo, se utiliza una programación en el paquete Stata 8.0 para especificar el modelo Logit dicotómico con datos tipo panel, cuyo resultado es un vector de parámetros con valores numéricos, que son los coeficientes para cada uno de las variables explicativas que hacen parte definitiva del modelo.

Para la estimación del modelo SARIMA se utiliza la metodología Box-Jenkins, que permite elegir de entre varios modelos, el que mejor represente el comportamiento de la serie. Es así como en el modelo SARIMA las proyecciones se basan únicamente en el comportamiento histórico de la inflación, es decir en las tendencias y ciclos que se presentan en la serie. Una vez estimado el modelo se utilizó el programa Eviews, con el que se realizó la metodología de ventanas rodantes fuera de muestra, del cual se obtuvo el pronóstico trimestral para el periodo 2005:4 - 2016:1.

Una de las ventajas que brinda esta metodología es que proporcionan predicciones óptimas tanto en plazo inmediato (un trimestre), como en el corto plazo, además esta metodología no necesita contar con varias series para realizar su estimación y pronóstico, pues se requiere tan sólo la serie a ser estudiada y sus rezagos.

Datos

Para la estimación del modelo de probabilidad logística Logit, se utilizan datos con periodicidad trimestral en Colombia, que abarcan el periodo muestral comprendido entre marzo de 2005 y diciembre de 2015, ya que el objetivo es analizar el traspaso del tipo de cambio a la inflación, así como la probabilidad de que el tipo de cambio se devalúe o se revalúe. Se analizan un total de 44 observaciones.

Teniendo en cuenta las variables más significativas que afectan a la devaluación y a su vez la identificación del efecto transmisión del tipo de cambio a la inflación, se hace un pronóstico de la inflación para los cuatro trimestres de 2016, para ello se utiliza una serie de tiempo estacionaria con datos históricos trimestrales de la inflación en Colombia para el periodo comprendido entre 2005 y 2015.

Estimación de Modelos

En esta estimación se tuvieron en cuenta los modelos LOGIT y SARIMA.

Modelo Logit

Se utilizó el modelo LOGIT, ya que la función logística es la función adecuada para determinar la probabilidad de que el tipo de cambio se devalúe o se revalúe. En este modelo logit la variable endógena es una variable dicotómica que toma valor 1 cuando hay devaluación (devaluacion positiva) y 0 cuando hay revaluación (devaluación negativa), se plantea desde la siguiente especificación general:

DEV=F( PIB,MS,XS,GAPPIB,TIINT,PRIMERATE )

Donde: DEV = Devaluación; PIB = Producto interno bruto colombiano; MS = Importaciones; MX = Exportaciones; GAPPIB = Brecha del producto; TIINT = Tasa de interés de intermediación del banco de la república; PRIMERATE= Tipo de interés externo.

Modelo SARIMA

Para realizar el pronóstico de la inflación trimestral de Colombia en 2016, se utilizó el modelo SARIMA, ya que con la información disponible de la serie temporal a estudiar se identificó que es un modelo autorregresivo (AR) de medias móviles (MA) y que además tiene un componente estacional, como se relaciona a continuación: SARIMA(411)4.

Donde: S = Identificador que la serie contiene un componente estacional; AR = Modelo auto regresivo; I = Integrado; MA = Modelo de medias móviles.

Se realiza la especificación del modelo SARIMA o identificación de los órdenes P,D,Q , ya que es estacional, luego se hace la estimación de los parámetros del modelo y se contrasta la validez del mismo. Finalmente se hace la predicción de los valores de la serie original para el periodo N + L (2016Q1, Q2, Q3, Q4).

Lo anterior se desarrolló mediante la metodología Box-Jenkins con los siguientes pasos: 1) Tomar una serie de datos trimestrales de inflación en Colombia de Marzo de 2005 a diciembre de 2015. 2) Iniciar la identificación con una representación gráfica de la variable para observar la estacionalidad, con la que se observan picos que parecen estar espaciados uniformemente, sugiriendo que hay presencia de periodicidad en la serie. 3) Eliminar la tendencia mediante diferenciación regular (y/o en la parte estacional), la cual se hizo con la primera diferencia. 4) Determinar el orden de los procesos autorregresivos y de medias móviles de los componentes regular y estacional. Esta decisión se toma mediante las funciones de autocorrelación total y parcial (FAC y FAP), con interpretación de los correlogramas. 5) Seleccionar el modelo AR(4) MA(1), con significancias menores al 1%. 6) Realizar el contraste de validez conjunta del modelo (R2, Sum Squared Resid, t, F).  7) Llevar a cabo el análisis detallado de los errores; correlograma de los errores (revisar ‘outliers’) . 8) Seleccionar el Modelo, para lo que se identificó el modelo SARIMA (4 1 1)4, con el cual se procede a la estimación de coeficientes del modelo. 9) Finalmente, realizar la predicción.

4. Resultados

A continuación se presentan los resultados de la investigación con base en datos recogidos en este estudio, para ellos se presentarán una tabla y figuras.

Resultados Modelo Logit

De acuerdo con los resultados de este modelo, las variables explicativas estadísticamente significativas son: en orden de significancia la TIINT, MS y XS. Fueron necesarias cinco iteraciones para estimar el modelo, la función LR chi2(6) = 31.49, el valor indica que los coeficientes son conjuntamente significativos para explicar la probabilidad de devaluación o revaluación; el p-valor de chi2 = 0.0000 indica que podemos rechazar la hipótesis de todos los coeficientes iguales a cero; el valor del pesado R2 = 0.5365 indica que aproximadamente el 53,65% de la variación de la devaluación es explicada por la variación de las variables independientes (TIINT, MS, XS).

Tabla 1: Resultados obtenidos del paquete STATA para el modelo Logit dicotómico

Standard errors in parentheses *** p<0.01, ** p<0.05, * p<0.1

Los signos obtenidos en la estimación de los parámetros de las variables explicativas corresponden con la teoría económica, es decir:

Tasa de interés de intermediación: Signo negativo (-207.5) ya que a un aumento de la TIINT se presenta revaluación de la moneda.

Importaciones: Signo positivo (0.00178), ya que un aumento de las importaciones genera mayor devaluación.

Exportaciones: Signo negativo (-0.00128), ya que a un aumento de las exportaciones generan una revaluación de la moneda colombiana.

Para medir la bondad del ajuste del modelo: Esta clases de valores correctamente clasificados que corresponde a 84,09%, que indica que el modelo en general provee el 84% de las observaciones correctamente. Mfx: Nos da el efecto marginal de las variables en términos de probabilidad, así el valor 0.2285, indica que la probabilidad que la tasa de cambio se devalúe es en promedio del 23% para esta muestra específica, la variable significativa con esta prueba es la TIINT, lo cual indica que el aumento del 1% en la tasa de interés de intermediación disminuye la probabilidad que la tasa de cambio se devalúe en un 36.58%. Esta gof: Nos indica que aceptamos la hipótesis nula de buen ajuste del modelo en un 47,69%.

Resultados Modelo SARIMA

La metodología de Box-Jenkins ofrece la manera de lograr el pronóstico a través de la construcción, identificación y predicción de un proceso Autorregresivo de Media Móvil Estacional, SARIMA, por tanto siguiendo esta metodología para la modelización de series univariantes se dispone de 44 datos trimestrales de la serie de inflación correspondientes al periodo primer trimestre de 2005 hasta el cuarto trimestre de 2015.

Para la estimación del modelo ARIMA es necesario que la serie (inflación) sea estacionaria. Si la serie no fuera estacionaria (como sucede en este caso de estudio), el modelo ARIMA tendría que ser estimado en sus primeras diferencias o si fuera el caso realizar una segunda diferencia.

Fig. 1
Serie de inflación en Colombia periodo 2005 - 2016

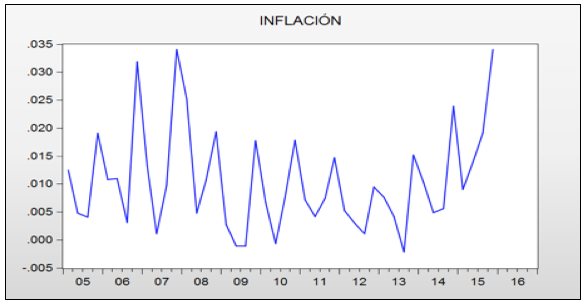
Para comprobar que la serie analizada es estacionaria se aplicó el test de Dickey Fuller Aumentado (ADF); en donde su valor (-1.439525) no resulta ser inferior a los valores críticos tanto al 1%, 5% y 10 %, lo cual nos lleva a aceptar la hipótesis nula de que la serie presenta raíz unitaria; es decir la serie no es estacionaria en media y en varianza, por tanto el modelo ARIMA se debe estimar en sus primeras diferencias.

Nuevamente se aplica el test de Dickey Fuller Aumentado (ADF); en donde su valor con la primera diferencia (-3.34.7271) resultó inferior a los valores críticos tanto al 5% como al 10 %, lo cual nos lleva a rechazar la hipótesis nula de que la serie presenta raíz unitaria; por tanto ahora la serie es estacionaria en media y en varianza.  

Dado que la serie ahora es estacionaria, se procede a la identificación del modelo; es decir determinar el orden del componente autorregresivo (p), así como también el orden del componente móvil (q). Para ello se procede a observar los correlogramas de las funciones de autocorrelación y autocorrelación parcial con el fin de determinar el modelo óptimo de proyección para la inflación.

Fig. 2
Correlograma de inflación

En el correlograma INFLACIÓN de la figura 3 se identificaron los coeficientes: AR (4) MA (1). Puesto que los datos de la serie analizada son trimestrales, Box-Jenkins recomiendan observar los rezagos 4, 8 y 12 con el fin de determinar la presencia o no de estacionalidad. Así, si observamos el correlograma anterior los rezagos 4 y 8 del componente autorregresivo muestran valores bajos, por lo que se podría intuir existencia de estacionalidad cada 4 trimestres 12.

El modelo ARIMA es ahora un modelo SARIMA, debido a que este tiene un componente estacional autorregresivo. El modelo quedaría expresado como: SARIMA (4.1.1)4.

De acuerdo al correlograma, el modelo óptimo es un SARIMA (4.1.1)4 según los criterios de información Akaike y Schwarz; pues éstos se minimizan en –7.008130 y –6.880163 respectivamente.

Fig. 3
Estimación del modelo SARIMA (4.1.1)4

Continuando con la metodología de Box y Jenkins el paso a seguir es la especificación del modelo, en el mismo que se analizará la significancia tanto individual como global de sus parámetros. Para este modelo todos los coeficientes resultaron estadísticamente significativos; pues los p valores son menores al 5% (95% de confianza); por ende, el modelo también posee significatividad global.

Los residuos de un modelo óptimo pueden ser ruido blanco, para lo cual se realiza el análisis de los residuos, para este modelo los correlogramas de los residuos presentan p valores menores al 5%, mostrando así coeficientes significativos. Por tanto, se puede decir que el modelo antes mencionado describe los datos trimestrales de la inflación de manera aceptable.

Fig. 4
Correlograma de Residuos

Finalmente, se realiza la predicción con el modelo SARIMA estimado que valida la consistencia del modelo de inflación colombiana realizando la proyección fuera de muestra mediante el uso de ventanas rodantes para el periodo 2005:4 – 2016:1; luego se realiza una comparación de la inflación estimada con la real, con el fin de establecer qué tanto se ajusta al modelo real.

La siguiente figura muestra los resultados del pronóstico de la inflación con el modelo SARIMA (4.1.1)4 donde se aprecia que el modelo captura la tendencia y la evolución de la inflación real presentada para los cuatro trimestres de 2016 que se ajusta a la tendencia de la serie real, mostrando que la inflación en 2016 ha sido la más alta en los últimos diez años.

Fig. 5
Pronóstico inflación con modelo SARIMA (4.1.1)4

5. Conclusiones 

El traspaso de la tasa de cambio a la inflación interna se realiza significativamente a través de la tasa de interés de intermediación, las exportaciones y las importaciones a corto plazo.

Un choque de la tasa de cambio genera un traspaso a través de la tasa de interés de intermediación, que afecta a la inflación negativamente en un 13.63%, de igual forma el traspaso de la tasa de cambio a la inflación a través de las exportaciones genera revaluación y por tanto una disminución de la inflación; finalmente la tasa de cambio hace un traspaso positivo a través de las importaciones del 0.00012% provocando un aumento poco significativo de la inflación.

Los resultados del modelo Logit aplicado a la devaluación en función de las variables explicativas que resultaron significativas de acuerdo con los signos, demuestran que la tasa de interés de intermediación es negativa, ya que un aumento de la TIINT presenta revaluación; las importaciones con signo positivo, representan un aumento de las importaciones que generan mayor devaluación y las exportaciones con signo negativo, un aumento de las exportaciones que generan una revaluación.

En términos de ajuste del modelo se concluye que el modelo en general prevee el 84% de las observaciones correctamente y que aceptamos la hipótesis nula de buen ajuste del modelo en un 47,69%.

Para realizar el pronóstico de la inflación trimestral de Colombia a 2016, se utilizó el modelo SARIMA, modelo autorregresivo (AR) de medias móviles (MA), que además tiene un componente estacional.

A partir de los datos históricos analizados y modelizados, se pronostica que el comportamiento de la inflación trimestral para el año 2016 podría reportar los siguientes datos: -5,91E-7, -7,53E-5, -849E-5 y 0.0003.

De acuerdo a la tendencia de la figura se observa que el comportamiento de la inflación para el año 2016 es similar a la de 2007 y 2015, siendo la inflación más alta de los últimos doce años.

Referencias

Hernández, C. F., Mesa, R. C. F. y Vélez-Pareja, I. (2009). Proyección De La Tasa De Cambio De Colombia Bajo Condiciones De Ppa: Evidencia Empírica Usando Var, http://www.redalyc.org/articulo.oa?id=89912259001, ISSN: 0120-1751, Rev. Colombiana de Estadística, vol. 32, núm. 2, pp. 157-187 (2009).

1. Escuela de Administración de Empresas de la Universidad Pedagógica y Tecnológica de Colombia, Calle 4 A Sur No. 15-134, Sogamoso, Boyacá, Colombia. Grupo de Investigación Management. Email: javier.gonzalezmillan@uptc.edu.co

2. Escuela de Administración de Empresas de la Universidad Pedagógica y Tecnológica de Colombia, Calle 4 A Sur No. 15-134, Sogamoso, Boyacá, Colombia. Grupo de Investigación OIKO. Email: nidea006@hotmail.com

3. Escuela de Administración de Empresas de la Universidad Pedagógica y Tecnológica de Colombia, Calle 4 A Sur No. 15-134, Sogamoso, Boyacá, Colombia. Grupo de Investigación Ceres. Email: ana.serrano@uptc.edu.co