ISSN 0798 1015

Vol. 39 (Nº 07) Año 2018. Pág. 16

Modelo cuantitativo ARIMAX- EGARCH para la predicción de la tasa de cambio colombiana (COP/USD)

ARIMAX-EGARCH quantitative model for prediction of the Colombian exchange rate (COP/USD)

Mario Alberto MARTÍNEZ Orozco 1; Diana Sirley GUZMÁN Aguilar 2; Fredy Ocaris PÉREZ Ramírez 3; Nini Johana MARÍN Rodríguez 4

Recibido: 12/10/2017 • Aprobado: 09/11/2017

Contenido

1. Introducción

2. Marco Teórico
3. Métodos de estimación y datos
4. Modelación y resultados
5. Conclusiones
Referencias
Anexos

1. Introducción

En el entorno económico actual, en donde el dólar sigue siendo la moneda de referencia a nivel mundial, es de vital importancia para las empresas del sector real y del sector financiero diseñar herramientas que les permitan obtener un mejor panorama para elecciones estratégicas que faciliten tener más opciones que les posibiliten las decisiones de inversión y tomar coberturas ante las fluctuaciones que se puedan presentar en la tasa de cambio, y a su vez, controlar y monitorear los riesgos a los que se exponen para no afectar el desempeño de sus operaciones. Igualmente, teniendo en cuenta la alta sensibilidad del peso colombiano a factores cualitativos y cuantitativos, tanto a nivel local como global, las compañías requieren de una planeación estratégica que facilite la toma de decisiones a corto y mediano plazo, permitiendo suavizar los impactos que generan los posibles choques exógenos en la economía dada la alta interdependencia de los mercados internacionales.

Para la realización de las operaciones en divisas, las empresas deben tener en cuenta factores importantes como el desempeño de las monedas de la región, publicación de datos macroeconómicos, volatilidad de los mercados, y que afectan la incertidumbre sobre el comportamiento de la paridad peso dólar. Para Caglayan & Demir (2014) este comportamiento puede afectar principalmente los costos de producción, el margen EBITDA, la capacidad de endeudamiento, puesto que le transmite volatilidad a cualquier operación no cubierta que requiera el uso de una moneda diferente a la nacional.

Del mismo modo, dentro de las actividades necesarias para no afectar la continuidad  de las operaciones que tengan una dependencia con la tasa de cambio, se encuentran la adquisición de obligaciones financieras en moneda extranjera, la compra y venta de insumos y commodities con el exterior, y la consolidación de estados financieros. A su vez,   cuando se reciben utilidades en otras monedas que en caso de incremento de la volatilidad de la tasa de cambio pueden verse comprometidas negativamente afectando la competitividad, reduciendo la rentabilidad e influenciando los resultados finales de la empresa.

El tipo de cambio se define como la cantidad de una moneda que se debe pagar por una unidad de otra divisa. Romero, Ramírez Elbar & Lozano Reyes (2007) definen el tipo de cambio como el precio de una moneda en función de otra. El valor de intercambio de las monedas en un tipo de cambio flexible se forma de acuerdo a las condiciones de oferta y demanda del mercado conforme al nivel actual de divisas en él. En cada país, las autoridades monetarias deben adoptar un régimen cambiario para determinar la forma en el cual va a fluctuar su moneda. Dicho régimen cambiario puede ser fijo, flexible, de banda cambiaria y dolarización, entre los sistemas más utilizados por las autoridades monetarias. Para el tipo de cambio fijo las autoridades monetarias establecen un valor para la divisa e intervienen en el mercado siendo oferente o demandante de divisas, para garantizar la cotización del tipo de cambio en rangos de precios previamente establecidos. Este tipo de régimen puede afectar la cantidad de reservas internacionales que se tienen. En un sistema de tipo de cambio flexible puro el banco central no interviene para controlar los precios y la cotización de la moneda está determinada por la demanda y oferta de la misma por parte de los agentes del mercado, lo anterior, sin perjuicio de que se puedan realizar intervenciones en algún momento e implementar operaciones de control de volatilidad para mitigar los efectos de cambios fuertes que puedan afectar la estabilidad de las economías.

Para Colombia en 1999 se implementó el régimen cambiario de flotación dirigida sin una trayectoria predeterminada del tipo de cambio, siendo un elemento fundamental para el logro de los objetivos del Banco de la República, ya que la flexibilidad cambiaria es importante como variable de ajuste ante los choques de la economía, pues permite utilizar de forma independiente las tasa de interés para alcanzar la inflación objetivo, pues esta última es el marco de política monetario de la economía. Es importante la coordinación de la política monetaria y cambiaria del país  para reducir los riesgos cambiarios por parte de los agentes del mercado, debido a la existencia de la trinidad imposible. Es decir, la dificultad con la que se enfrentan los gobiernos para mantener la competitividad de la economía sin descuidar otras variables económicas. Se debe aclarar, que el emisor tiene establecidas subastas de control de volatilidad para intervenir en un momento determinado y  controlar cambios abruptos que se puedan presentar en las cotizaciones.

Este estudio tiene como propósito identificar un modelo cuantitativo de la familia ARIMAX-GARCH con el objeto de pronosticar la tasa de cambio colombiana (COP/USD). Para ello el artículo está organizado de la siguiente manera: en la primera sección, se hace una revisión teórica de las variables que afectan el tipo de cambio a nivel nacional e internacional. En la segunda sección, se presenta la descripción general delos modelos que componen la familia ARIMAX-GARCH como metodología útil para los pronósticos del tipo de cambio. En la tercera sección, se describen los principales resultados obtenidos y, por último, se presentan unas conclusiones.

En los últimos años, se han venido desarrollando estudios e investigaciones que buscan obtener pronósticos  del comportamiento de los tipos de cambio a nivel nacional e internacional, los cuales se constituyen en un punto de partida para esta investigación.

En el 2002 en Australia Peramunetilleke & Wong (2002) realizó un estudio en donde se analizó como las noticias pueden ser usadas para pronosticar los movimientos de la tasa de cambio. La innovación contenida en esta investigación muestra que, contrario a los análisis realizados con base en información cuantificable, los pronósticos se hacen con base al estado actual de los mercados financieros, así como noticias políticas y evolución de los fundamentales macroeconómicos en general.

En el 2006 Velásquez Henao & Gonzáles Rivera (2006) realizó un trabajo en Colombia utilizando el modelo de redes neuronales artificiales en donde se encontró que este modelo explica la dinámica del comportamiento del tipo de cambio comparado con un modelo lineal autorregresivo. Los resultados finales muestran que se debe analizar la capacidad de predicción de cada metodología de acuerdo a las características de cada serie y cuál modelo la puede representar mejor.

Por otro lado, Cárdenas y Ojeda (2010), estudia un modelo sustentado en los fundamentos de la regla de Taylor para evaluar la previsibilidad de la tasa de cambio nominal de seis divisas latinoamericanas: el peso argentino, el peso chileno, el peso colombiano, el peso mexicano, el peso uruguayo y el real brasileño con respecto al dólar norteamericano; utilizando estrategias econométricas, que llevaron a resultados importantes. Encontraron que  el modelo basado en las reglas de Taylor, permite obtener pronósticos fuera de muestra superiores a los realizados por un modelo de caminata aleatoria para las seis divisas analizadas. Dicho trabajo es importante para esta investigación, debido a que es un método alternativo para obtener predicciones de la tasa de cambio y que podría ser comparado con los resultados obtenidos en la investigación.

Apergis, Zestos & Shaltayev (2012) modelan una tasa de cambio dólar – euro óptima para los países de la unión europea, basados en la relación causal entra el tipo de cambio dólar-euro y tres variables macroeconómicas clave: la balanza comercial global de Estados Unidos  con el resto del mundo, el diferencial de tasas de interés (spread) entre EE.UU. y la Unión Europea y el precio de un barril de petróleo expresado en dólares estadounidenses. La investigación es llevada a cabo utilizando un vector autorregresivo de corrección de errores (ECVAR, por sus siglas en inglés). Los hallazgos muestran una evidencia a favor de relación existente entre el tipo de cambio y el diferencial entre los tipos de interés estadounidenses y de la Zona Euro. Los resultados  muestran que, a largo y corto plazo existe, una relación causal unidireccional desde los diferenciales de tasas de interés hacia la tasa de cambio dólar – euro. Lo que implica, que los bancos centrales de ambas monedas pueden incidir en la variación de la tasa de cambio.

De la misma manera, Apergis (2014) realizó un estudio sobre si los precios del oro tienen una relación con la tasa de cambio dólar australiano en el periodo 2000 – 2012. A través de un modelo de corrección de errores, los resultados mostraron que fuera de la muestra la capacidad predictiva del precio del oro tiene incidencia en el desempeño del dólar australiano en los horizontes de corto y mediano plazo comparado con un modelo de predicción de caminata aleatoria. Estos resultados pueden ser útiles en términos de disponibilidad de información para los exportadores de oro, para las autoridades monetarias, administradores de fondos y gestores de fondos de inversión. En el último año también se han desarrollado predicciones de series de tiempo por Corrêa, Neto, Teixeira Júnior, Franco & Faria (2016), quienes por medio de un modelo WARIMAX – GARCH, (Wavelet Auto-Regressive Integrated Moving Average with exogenous variables and Generalized Auto-Regressive Conditional Heteroscedasticity), el termino wavelet tiene que ver con movimiento pequeño de onda a partir de la serie subyacente y da como resultado un modelo de ARIMA con variable exógena con movimiento de onda ,y que en base a dicho movimiento podría mejorar la predicción.

Para la elaboración de pronósticos de una paridad cambiaria se deben revisar los factores que afectan el comportamiento de la tasa de cambio COP/USD, identificar las variables que tienen incidencia en su comportamiento, y su vez, desarrollar la metodología empleada para la construcción del modelo de predicción.

3.1. Factores que inciden en el tipo de cambio en un régimen cambiario de tipo de cambio flexible

El dólar es una de las monedas más importantes a nivel global, y a su vez, la divisa de referencia para todas las transacciones internacionales en Colombia y en el mundo en general, por consiguiente, es importante revisar los factores que interviene en su comportamiento. De acuerdo a un estudio realizado por Apergis, Zestos & Shaltayev (2012),  los enfoques para el estudio de las divisas pueden clasificarse en dos categorías: el equilibrio fundamental y el comportamiento del tipo de cambio. La primera busca la combinación correcta de los fundamentales macroeconómicos, refiriéndose a los factores que inciden en la demanda y oferta  del mercado en que se cotiza la moneda, y la segunda hace referencia a las variaciones que tienen los activos en los mercados. Todos los hechos que afectan los tipos de cambio se conocen como fundamentales macroeconómicos o de mercado, y son los que se espera sean capaces de predecir con alguna precisión el movimiento de los tipos de cambio. Igualmente,  existen factores económicos de corto y largo plazo determinantes de las variaciones en la tasa de cambio. Para Due, Iglesias-Fernández & Llorente-Heras (2015) los elementos de corto plazo pueden ser relacionados con las variaciones constantes de los niveles de oferta y demanda del activo: órdenes de mercado; desempeño de índices bursátiles de las principales bolsas como S&P 500, Nasdaq y DAX; liquidez de mercado; precio de los commodities; noticias económicas como la publicación de datos de crecimiento económico, inflación, decisiones de política monetaria y balanza cambiaria; las cuales tendrán el grado de afectación dependiendo de la fortaleza actual de cada economía.

Por otra parte, los efectos de largo plazo obedecen más al comportamiento de los fundamentales de las economías como la cuenta corriente, las reservas internacionales y la calificación de la deuda soberana. Estos factores al ser de carácter económico generalmente se prolongan por periodos más largos y por lo tanto son más estructurales. Las economías de países emergentes cuyas monedas tienen poca aceptación comercial en el mundo deben tomar como referencia divisas fuertes como el dólar, euro o la libra esterlina. El tener una moneda fuerte como referencia, y en especial el dólar estadounidense, es contar un activo que intervenga en la mayoría de transacciones comerciales, que sirva de reserva para los bancos centrales, y en el caso de países exportadores como los emergentes, que dependen en gran parte de sus exportaciones, pueden generar facilidad al momento de hacer sus transacciones. Por lo tanto, el comportamiento del tipo de cambio tiene una influencia directa en la economía de los diferentes países emergentes afectando los términos de intercambio.

Las variaciones del tipo de cambio vía revaluación (disminución del precio que hay que pagar en moneda nacional por unidad extranjera) o devaluación (aumento del precio que hay que pagar en moneda nacional por unidad extranjera), y esto afecta a diferentes sectores económicos en mayor o menor grado, dependiendo del grado de especialización y actividad económica en el que se desenvuelvan. Los países industrializados al tener sistemas económicos fuertes y monedas referentes a nivel mundial deben experimentar pocos desequilibrios económicos por una crisis de tipos de cambio. Por otra parte, las economías emergentes inmediatamente sufren la salida de grandes flujos de capital tanto de inversión de portafolio como inversión extranjera directa (IED) generando contracciones económicas, Calvo & Reinhart (1999).

Entre 2012-2015 en Colombia se perdieron los términos de intercambio favorables para la moneda relacionados con los altos precios del petróleo como se muestra en Toro, Garavito, López & Montes (2015), lo cual permitió una gran entrada de recursos a la economía vía IED que se tradujeron en una revaluación del tipo de cambio. Estos hechos crearon la necesidad de que los agentes y empresas que intervienen en los mercados de divisas deban tener herramientas enfocadas en mejorar su gestión. De esta manera, se generó la necesidad de obtener mecanismos que les permitiera pronosticar el precio de la tasa de cambio en función de las variables que afectan su comportamiento. Las variables que pueden tener incidencia en su variación pueden ser de carácter endógeno o exógeno, y como se ha mencionado anteriormente, pueden ser de corto y largo plazo y afectan el comportamiento de las cotizaciones del tipo de cambio en diferentes periodos.

Por lo tanto, se hace notable la aplicación de  métodos cuantitativos para pronosticar el comportamiento de la paridad peso colombiano-dólar y su utilidad para emplearla en las decisiones estratégicas tomadas por las empresas. Es así como en esta investigación se aplicó un modelo cuantitativo para la elaboración del pronóstico de la tasa de cambio con base en las variables exógenas que puedan incidir directamente en su comportamiento, para lo cual se seleccionaron variables tanto de corto plazo como de largo plazo.

Para la selección de las variables a tener en cuenta para la construcción del modelo inicial se tomaron series financieras que tuvieran una publicación de datos diaria, considerando que hay variables importantes que pueden afectar el comportamiento de la moneda como la publicación del IPC (Índice de precios al consumidor), crecimiento económico, decisiones de tasas de interés, reservas internacionales, las cuales pueden tener efectos tardíos en el desempeño del tipo de cambio debido a su publicación mensual o trimestral,  y por esta razón no fueron incluidas en la selección de variables para la construcción del modelo de predicción.  Las variables seleccionadas se describen brevemente en la siguiente tabla.

Tabla 1
Variables que afectan la cotización de la tasa de cambio en Colombia

Fuente: Bloomberg – Elaboración propia.

3.2. Modelos ARIMA y ARIMAX

La metodología que se utilizará para la realización del pronóstico es el modelo integrado autorregresivo y de medias móviles (ARIMA); su utilidad ha sido importante por su facilidad de ajuste a una serie de tiempo y ha venido siendo empleada regularmente por diferentes investigaciones en los últimos años.

Los Modelos ARIMA fueron propuestos por Box and Jenkins (1970) para series de tiempo estacionarias que tengan auto-dependencia lineal. Se desarrollaron con el objetivo principal de estimar y predecir su comportamiento basado en el comportamiento pasado de la misma serie. Se obtienen de tres factores, la primera se refiere a los valores rezagados de la serie (AR), la segunda se obtiene por medio de los rezagos de los errores  que se originan por el carácter estocástico (MA), y el tercer es el factor de diferenciación que debe tener a serie para la estimación del modelo (I). Dicho modelo se basa en datos históricos de series temporales cuantificando patrones autorregresivos y de media móvil para producir los pronósticos. Para su correcta utilización se requiere que la serie sea estacionaria, o transformarla en ella. Un modelo ARMA (p,q) está representado por la siguiente formula:

El modelo tiene varios supuestos estadísticos que se deben seguir para asegurar la validez de los resultados del modelo, los cuales se describirán a continuación.

3.3. Supuestos del modelo

3.3.1. Como requisito fundamental el proceso debe ser estacionario, tanto en media como en varianza.

3.3.2. Los residuos del modelo deben ser incorrelacionados.

3.3.3. El coeficiente estimado de una variable exógena debe ser significativo en su probabilidad.

3.3.4. No tener evidencias de causalidad inversa entre la variable exógena y la variable dependiente.

3.3.5. Las variables exógenas del modelo no deben un alto grado de multicolinealidad.

3.4. Familia de Modelos ARCH

En estos modelos, se supone que la varianza condicional de la serie no es constante en el tiempo. Las series de tiempo a menudo pueden tener periodos de alta volatilidad seguidos de momentos de relativa calma. Para esto Engle (1982) desarrolló la familia de modelos ARCH que permiten que la varianza condicional sea explicada por valores pasados de la misma varianza. El modelo realiza la predicción de la varianza en función de variables observables actuales, a su vez proponía usar medias ponderadas de los cuadrados de los errores, es decir, un tipo de varianza ponderada. El modelo ARCH (1) tiene la siguiente ecuación:

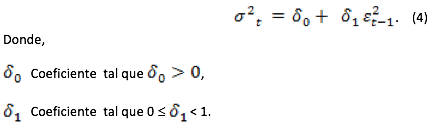
Al poco de tiempo, Bollerslev (1986) desarrolló la primera generalización del modelo ARCH logrando un modelo autorregresivo de medias móviles nombrado GARCH. En dicho modelo la predicción de la varianza se hace por medio de una ponderación de la misma de tres predicciones diferentes. La primera es una varianza constante que tiende a ser la media de largo plazo. La segunda es la predicción del periodo anterior, y la tercera es una nueva predicción del periodo anterior con nueva información que no estaba disponible cuando se hizo la predicción. La ponderación de las tres predicciones nombradas es lo que determina el cambio en la varianza.

El modelo GARCH (1, 1) es el más empleado para describir la dinámica de la volatilidad de una gran serie de rendimientos financieros como lo explica Engle (2004) y es utilizado generalmente como el punto de partida para la predicción de la volatilidad. La ecuación de un modelo GARCH (1, 1) es:

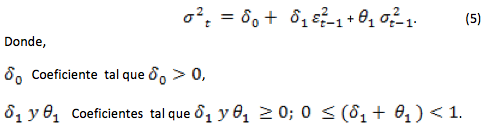
De la misma forma, más adelante Nelson (1991) desarrolló la segunda generalización de la familia de modelos ARCH por medio del GARCH exponencial o EGARCH en el que se descubre que la volatilidad podía responder de forma asimétrica a errores de predicción pasados. Si tiene en cuenta un contexto financiero, se evidencia en su investigación que los  rendimientos negativos parecían ser predictores de volatilidad en una mayor proporción que los positivos, lo que demostraba que las caídas fuertes muestran pronósticos de una mayor volatilidad que las que arroja un incremento en los precios de la misma magnitud. La ecuación para el modelo EGARCH es:

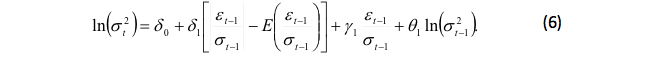
Es importante tener en cuenta que el modelo EGARCH permite que tanto las buenas como las malas noticias tengan efectos diferentes sobre la volatilidad, mientras que el GARCH no permiten hacerlo.

La familia de modelos ARCH aunque es aplicable a cualquier serie temporal ha sido muy exitosa aplicándola a las series financieras debido a las características que tienen que tienen sus rendimientos. Estas características principales son que los rendimientos tienen carácter impredecible, esto es, poseen  valores extremos y  tanto los periodos de calma como los volátiles están agrupados en el tiempo. Los procesos ARCH pueden predecir patrones dinámicos de regreso a la media. Para el caso analizado, el objetivo de incluir este tipo de modelos es el de eliminar la heteroscedasticidad en la varianza.

3.5. Datos

Para la construcción del modelo se utilizó la serie de precios de la paridad COP/USD  considerando una muestra de datos que comprende desde 4 de enero de 2010 hasta el 13 de enero de 2017 para un total de 1834 registros diarios con una frecuencia de cinco datos por semana. Para obtener la serie de cinco datos por semana no se incluyeron los fines de semana, y para el caso de los festivos se utilizó el dato anterior conocido.

En el gráfico 1 se puede observar el comportamiento de las cotizaciones diarias de COP/USD en el eje izquierdo, y a su vez los rendimientos logarítmicos diarios en el periodo de la muestra en el eje derecho. En este gráfico se observa que la serie de precios no se mantiene en un rango definido por lo que se evidencia la existencia de una tendencia que indica que la serie de precios puede no ser estacionaria en media, y por lo tanto, se debe transformar la serie. La transformación se realizó calculando los rendimientos logarítmicos diarios de la serie. La serie de rendimientos muestra que tiene una estabilización en media en el periodo analizado pero se evidencia una estructura de dependencia temporal que está asociada con aumentos de la volatilidad de los precios en los períodos de caída de los precios. Adicionalmente, en este gráfico se evidencia que la serie no tiene un componente estacional en su comportamiento ya que no se observan variaciones cíclicas predecibles y no presenta un comportamiento que sea similar en periodos inferiores a un año.

Gráfico 1
Comportamiento de Precios y Rentabilidad del COP/USD entre Enero de 2010 y Enero de 2017

Fuente: Datos Extraídos de Bloomberg – Elaboración Propia.

En el gráfico 1 también se puede apreciar otra característica importante de los rendimientos que es el agrupamiento de la volatilidad (Volatility Clustering), lo que  indica que en el momento en el que la volatilidad sea baja permanecerá de esa forma y cuando la volatilidad sea elevada perdurará alta. Adicionalmente, se verifica que existe estructura de dependencia temporal de la serie y que por tanto existe efecto ARCH, por lo cual se hace necesario remover dicha estructura de dependencia temporal mediante un modelo ARMA-GARCH.

3.6. Análisis de los rendimientos

En el gráfico 2 se muestra uno de los hechos estilizados de los rendimientos de activos financieros (Alonso & Arcos, 2006) que es tener una distribución leptocúrtica en la que se pueden ver picos más altos y colas más pesadas respecto al comparativo con la función de distribución normal como es de esperarse en una serie de rendimientos financieros. Para este caso, se evidencia que existe la posibilidad de tener más valores extremos para el lado derecho de la distribución. Las colas pesadas implican la probabilidad de obtener valores extremos en sus rendimientos comparados a los que se esperaría de una distribución normal. Igualmente se presenta un coeficiente de curtosis igual a 9,54, el cual es evidentemente mayor al que posee una distribución normal que es de 3. Además, el Jarque Bera comprueba la no normalidad de la serie.

Gráfico 2
Histograma y Estadísticos Principales COP/USD 

Fuente: Datos Extraídos de Bloomberg – Elaboración Propia.

4.1. Identificación de la Estructura ARIMAX

Para la estimación del modelo para pronosticar el valor futuro de la paridad COP/USD en media se utiliza la metodología ARIMA desarrollada por Box and Jenkins (1970), y para la eliminación de la heteroscedasticiad de la volatilidad se utilizarán los modelos de la familia ARCH con sus extensiones, específicamente el modelo EGARCH que explica mejor los efectos tanto negativos como positivos de la volatilidad.

Para la construcción inicial del modelo ARIMAX se tomó como variable dependiente a la serie COP/USD y como variables exógenas o independientes a las series de retornos del precio del petróleo (WTI), Índice DXY, Índice LACI, Índice de Volatilidad VIX, el precio del Oro y Tesoros de Estados Unidos con vencimiento a 10 años.  Para la escogencia de estas series se tomaron variables que de acuerdo a su nivel de importancia que puedan afectar el comportamiento diario la tasa de cambio, que sean publicados diariamente, que no sean de publicación rezagada ya que pueden mostrar cambios en forma tardía y pueden perder su valor predictivo, y que su vez, se pudieran consultar en tiempo real durante la negociación de mercado, permitiendo tener actualizado su pronóstico en el momento que sea necesario para la toma de decisiones.

Para el desarrollo del modelo de predicción se verificó que todas las variables utilizadas fueran estacionarias. Para revisar esta propiedad se realizaron pruebas de raíz unitaria para cada serie de precios original mediante la prueba de Dickey Fuller Aumentada (ADF, por sus siglas en inglés Augmented Dickey-Fuller test), cuya hipótesis nula es que existe una raíz unitaria en la serie. Según los resultados encontrados se evidencia que las series de precios originales analizadas presentan raíz unitaria, y por lo tanto, las series deben transformadas ejecutando la diferencia en primer orden para obtener series I(0), es decir, estacionarias. Los resultados de las pruebas ADF aplicando a la primera diferencia de las series se muestran en la Tabla 2. La prueba se realizó tomando un nivel de significancia del 5% en donde se observa que el valor p de cada variable es menor al 5%, lo cual conduce a rechazar la hipótesis nula de raíz unitaria. De esta manera, las series de rendimientos diarios analizados son estacionarias en media y son adecuadas para aplicar la metodología de construcción de modelos ARIMAX.

Tabla 2
Prueba de raíz unitaria: Prueba Dickey Fuller Aumentado (ADF)

Fuente: Datos Extraídos de Bloomberg – Elaboración Propia.

Adicionalmente, es importante identificar si existen relaciones de causalidad entre las variables del modelo, mediante la metodología propuesta por Granger (1969) denominada prueba de Causalidad de Granger, la cual permite identificar las relaciones de causalidad entre las variables exógenas y la variable respuesta. Su objetivo es determinar una variable X causa el movimiento de la otra variable Y, esto no significa que Y sea el resultado de X porque pueden intervenir factores adicionales en el resultado de la variable.

La prueba se realizó para todas las variables exógenas resultantes del modelo contra la variable respuesta del mismo. Para que no exista doble causalidad entre las variables que se incluyen en el modelo se debe validar que el valor p de la causalidad de la variable exógena contra la variable dependiente sea menor al 5%. Del mismo, se evalúa la causalidad de la variable dependiente contra la exógena en la cual su valor p no debe ser significativo, si se cumplen estas dos condiciones las variables pueden hacer parte del modelo de predicción. En la tabla 3, se muestran los resultados de las pruebas realizadas. En esta tabla se puede observar que las variables VIX y Tesoros de 10 años tienen causalidad doble con el tipo de cambio por lo que debieron ser removidas de la ecuación final. Las otras variables cumplen con las condiciones propuestas por la metodología y, por lo tanto, pueden ser utilizadas para la construcción modelo de predicción.

Tabla 3
Prueba de Causalidad de Granger

Fuente: Datos Extraídos de Bloomberg – Elaboración Propia.

4.2. Implementación de la metodología ARIMAX

Para comenzar la construcción del modelo que permite realizar el pronóstico de la variable dependiente se observaron los gráficos ACF y PACF  para los rendimientos diarios de la serie COP/USD con el objetivo de encontrar el orden de la serie temporal y la estructura ARIMAX. Por consiguiente, el primer paso es la elaboración del proceso iterativo para analizar las variables cuyos coeficientes sean significativos para explicar el comportamiento de la variable respuesta, es decir, el tipo de cambio COP/USD. Durante este proceso, se identificó la estructura AR de la serie. Dentro de los resultados se encontró Modelo ARIMAX tiene las variables con su valor p significativos  con una confianza del 95% para las variables de retornos de los precios del petróleo, del índice LACI, del Dollar Index (DXY) y algunos rezagos.

En el proceso de construcción del modelo se evalúo la estructura ARIMAX estimado y se encontró que su estructura solo tiene parámetros autorregresivos con rezago 2 y 12, es decir, ARMAX(12,0), los cuales resultaron significativos y pueden explicar el comportamiento en media de la variable respuesta. Además, no se incluyó la parte de media móvil por resultar no significativa. Este resultado indica que una variación del 1% en los rendimientos de la tasa de cambio de hoy se ven reflejados en la tasa de cambio en promedio a los dos y 12 días.

Para verificar que las especificaciones del modelo ARIMAX fueran adecuadas se realizó la prueba de autocorrelación del estadístico Ljung Box por medio del análisis del correlograma de los residuos del modelo ARMAX(12,0) en niveles. En el anexo 1 se presenta el correlograma de los residuales del modelo en niveles, en el cual se observó que al remover la estructura de dependencia temporal en media mediante la aplicación del modelo propuesto, los residuales resultaron ser estacionarios, pues tanto el estadístico Q como el valor p indicaron que dichos residuales son ruido blanco y no están autocorrelacionados, confirmado que el modelo propuesto estuvieron bien identificado. Por otra parte, el resultado del análisis de los residuales al cuadrado del modelo ARMAX(12,0) por medio del correlograma evidencian la existencia de efectos ARCH, es decir, se verifica que dicho modelo presenta volatilidad condicional heteroscedástica pues todos los valores p son menores al 5%, con lo cual se rechaza la hipótesis nula de no autocorrelación serial de los residuales, indicando la posible la existencia de estructura de dependencia temporal en varianza de dicha serie.

Para corregir la estructura de dependencia temporal  en varianza se procedió a estimar la varianza condicional por medio de la familia de modelos ARCH para la estabilización de la misma. En este caso se  utilizó el modelo EGARCH (1,1). De esta manera, para modelar conjuntamente media y varianza de las series de retornos se utilizó el modelo ARMAX(12,0)-EGARCH(1,1). Dicho modelo contempla una característica muy importante como lo es el efecto de asimetría en la volatilidad, el cual postula que la volatilidad en los precios es mayor cuando los precios de los activos están en tendencia negativa comparados con predicciones de volatilidad en mercados al alza.

El resultado del test ARCH-LM obtenido para el modelo ARMAX(12,0)-EGARCH(1,1) se puede observar en la Tabla 4. Es ésta, se puede analizar que en los residuos al cuadrado no se encuentra evidencia a favor de la existencia de efectos ARCH ya que según se puede ver los valores p son superiores al 5% en todos los casos. Luego de la estimación de la varianza por medio del modelo ARMAX(12,0)-EGARCH(1,1) se vuelve a realizar el correlograma de los residuos y de los residuos al cuadrado los cuales muestran que los valores p son superiores al 5%, por lo tanto, los residuales del modelo son ruido blanco, por lo que se puede concluir que con dicho modelo se remueve la estructura de dependencia temporal en varianza, ver anexo 2.

Tabla 4
Test ARCH LM del modelo ARMAX(12,0)-EGARCH(1,1)

Fuente: Datos Extraídos de Bloomberg – Elaboración Propia.

En la tabla 5, se presentan los resultados del modelo estimado.

Tabla 5
Tabla de Estimación Modelo ARMAX(12,0)-EGARCH(1,1)

Fuente: Datos Extraídos de Bloomberg – Elaboración Propia.

Para la distribución de los errores del modelo se utilizó la función GED (Distribución de errores generalizada) propuesta por Nelson (1994). En la tabla 5, se observa que el parámetro estimado de dicha distribución es 1,1063, indicando que la distribución de los retornos diarios de la tasa de cambio corregidos por la media es leptocúrtica.

4.3. Análisis de los resultados y pronóstico del modelo seleccionado

El modelo calculado para la determinación de la tasa de cambio con fines de pronóstico es un ARMAX(12,1,0)-EGARCH(1,1). Los resultados de la estimación son presentados en la tabla 5. Así, se puede apreciar como por cada punto porcentual que se incremente el retorno diario del petróleo WTI (CL1) en el instante t se espera que en promedio el retorno diario de la tasa de  cambio se disminuya en 0.042%.  Esto quiere decir, que un cambio de 1% en el rendimiento del crudo WTI hoy afecta inmediatamente el rendimiento de la tasa de cambio con una disminución en promedio de 0.042%.

Igualmente, los resultados obtenidos para las demás variables exógenas incluidas en el modelo se pueden ver en la tabla 5. Aquí se observa que por cada punto porcentual que se incremente el retorno diario del índice LACI en el día t se espera que en promedio el retorno diario de la tasa de cambio se disminuya en 0.35%. De igual forma, por cada punto porcentual que se incremente el retorno diario del índice LACI en el día t se espera que en promedio el retorno diario de la tasa de cambio se disminuya en 0.14% en el período t-1. Igualmente, por cada punto porcentual que se incremente el retorno diario del índice LACI en el día t se espera que en promedio el retorno diario de la tasa de cambio se incremente en 0.059% en el período t-7.

Así mismo, por cada 100 puntos básicos que se incremente el retorno diario del índice DXY, se espera que en promedio el retorno diario de la tasa de cambio aumente en 7,5 puntos básicos en el período t y disminuya 7,4 puntos básicos en el período t-2. En forma análoga se interpretan los demás resultados para los retornos de los rezagos del COP/USD y el precio del oro (GC1).

Estos hallazgos muestran que los retornos diarios de la tasa cambio COP/USD es afectada por las variaciones diarias de las variables exógenas analizadas y estaría respondiendo a los cambios constantes en las cotizaciones de los activos en el mercado de valores.  Además, los resultados también arrojan que el valor pronosticado de los retornos diarios de la tasa de cambio COP/USD se va a ver afectado inmediatamente (período t) por la cotización en el mercado del precio del petróleo WTI (CL1), el índice LACI y el índice DXY; hecho que es coherente con los hechos estilizados al ser variables con una alta liquidez en los mercados que cotizan y generan una actualización constante.

La representación matemática del modelo ARMAX(12,1,0)-EGARCH(1,1) para estimar en media la rentabilidad de la paridad COP/USD es:

La ecuación de la varianza del modelo ARMAX(12,1,0)-EGARCH(1,1) se representa de la siguiente forma:

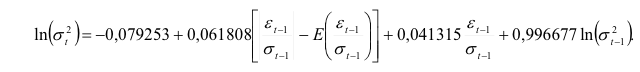
En el gráfico 3 se pueden observar los resultados del pronóstico realizado por el modelo en un periodo de tres meses en el que se incluyen el precio observado de la moneda y el pronóstico muestral. Adicionalmente, se presenta el resultado de la predicción extra-muestral de cinco observaciones. Como resultado se observa como los rendimientos pronosticados de la tasa de cambio por el modelo ARMAX(12,1,0)-EGARCH(1,1) siguen de cerca los datos observados muestrales y extramuestrales. Esto hace que el resultado de la predicción pueda ser utilizado para la toma de decisiones de inversión con una mayor confianza.

Gráfico 3
Comparativo Pronóstico Muestral, Extramuestral y Precio Actual (observado) del COP/USD

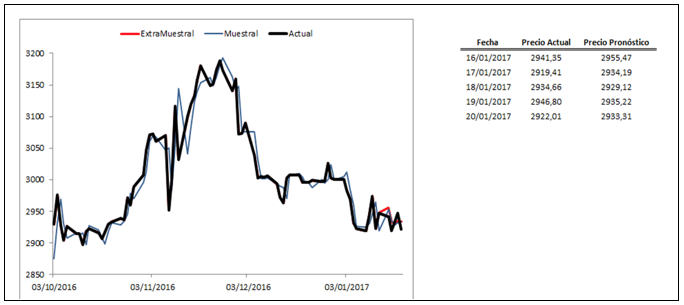
Fuente: Datos Extraídos de Bloomberg – Elaboración Propia.

El comportamiento de la tasa de cambio  influye en la operación de la mayoría de las empresas tanto privadas como públicas en Colombia, por lo cual su desempeño ha ganado la atención, especialmente el tener certeza sobre su comportamiento futuro. Por lo tanto,  es muy importante cuantificar y entender sus determinantes, y a su vez, contar con herramientas que permitan la toma de decisiones. Para este propósito, en la administración del riesgo asociado a su determinación se debe hacer énfasis en la identificación de los elementos que, directa o indirectamente, inciden en su evolución y de esta manera aprovechar las oportunidades que genera su predicción, así como minimizar los impactos que genera su volatilidad. Por esta razón, se hace importante el desarrollo de modelos de predicción con variables exógenas como el modelo ARIMAX o ARIMAX-EGARCH.

Los resultados obtenidos muestran que la implementación de modelos que incluyan variables exógenas en la predicción puede potenciar los resultados de estimación y permite obtener resultados más coherentes con los hechos estilizados que presenta la evolución de los mercados. De la misma manera, el pronóstico realizado por el modelo ARIMAX-EGARCH destaca la flexibilidad que tiene este tipo de modelos en el que se observa que los datos estimados por el modelo siguen de cerca los datos observados. Para los datos pronosticados de forma extramuestral, la variación es en promedio de 4,61 pesos con respecto a los precios observados de la tasa de cambio indicando relativamente poca variación.

En esta investigación se encontró como el comportamiento de los rendimientos de la tasa de cambio COP/USD puede ser estimado mediante la implementación del modelo ARMAX(12,1,0)-EGARCH(1,1), en donde los retornos diarios de la tasa de cambio COP/USD se ven afectados inmediatamente (período t) y de forma negativa por la cotización en el mercado del precio del petróleo WTI (CL1), el índice LACI y positivamente por el índice DXY; hecho que es coherente con los hechos estilizados al ser variables con una alta liquidez en los mercados que cotizan y generan una actualización constante. Además, el rezago 1 (período t-1) de los retornos del índice LACI impacta positivamente el retorno diario de la tasa de cambio y el rezago 7 (período t-7) de los retornos del índice LACI y el precio del oro (GC1) afectan positiva y negativamente, de forma respectiva al retorno diario de la tasa de cambio. Por último, los rezagos 2 y 12 (períodos t-2 y t-12) de los rendimientos de la tasa de cambio COP/USD afectan negativamente los rendimientos actuales (período t).

El modelo de predicción calculado ARMAX(12,1,0)-EGARCH(1,1) permite que ante cualquier variación de las series utilizadas (en el período indicado), el pronóstico de la tasa de cambio se actualice inmediatamente; brindando una fuente de información confiable para la toma de decisiones de inversión que adapta la dinámica de los retornos de la tasa de cambio y las demás variables en los mercados de valores con fines de pronóstico de la tasa de cambio.

Alonso, J. C., & Arcos, M. A. (2006). Cuatro hechos estilizados de las series de rendimientos: una ilustración para Colombia. Estudios Gerenciales, 103–124.

Apergis, N. (2014). Can gold prices forecast the Australian dollar movements? International Review of Economics and Finance, 29, 75–82. https://doi.org/10.1016/j.iref.2013.04.004

Apergis, N., Zestos, G. K., & Shaltayev, D. S. (2012). Do market fundamentals determine the Dollar-Euro exchange rate? Journal of Policy Modeling, 34(1), 1–15. https://doi.org/10.1016/j.jpolmod.2011.10.003

Bollerslev, T. (University of C. at S. D. (1986). Generalized Autoregresive Conditional Heteroskedasticity. Journal of Econometrics, 31(3), 307–327. https://doi.org/10.1109/TNN.2007.902962

Box, G.E.P. and J.M. Jenkins, 1976, Time series analysis: Forecasting and control (Holden-Day, San Francisco, CA).

Caglayan, M., & Demir, F. (2014). Firm Productivity, Exchange Rate Movements, Sources of Finance, and Export Orientation. World Development, 54, 204–219. https://doi.org/10.1016/j.worlddev.2013.08.012

Calvo, G. A., & Reinhart, C. M. (1999). Capital Flow Reversals, the Exchange Rate Debate, and Dollarization More. Finance & Development, (September), 13–15.

Cárdenas, D. & Ojeda, J. (2010). "Reglas de Taylor y previsibilidad fuera de muestra de la tasa de cambio en Latinoamérica", Borradores de Economía 619, Banco de la República de Colombia. Retrieved from http://www.banrep.org/docum/ftp/borra619.pdf

Corrêa, J. M., Neto, A. C., Teixeira Júnior, L. A., Franco, E. M. C., & Faria, A. E. (2016). Time series forecasting with the WARIMAX-GARCH method. Neurocomputing, 216, 805–815. https://doi.org/10.1016/j.neucom.2016.08.046

Due, D., Iglesias-Fernández, C., & Llorente-Heras, R. (2015). Determinantes de la tasa de cambio en Colombia: un enfoque de microestructura de mercados. Ensayos Sobre Política Económica, 33(74), 207–219. https://doi.org/10.1016/j.espe.2015.09.001

Engle, R. (2004). Riesgo y Volatilidad : Modelos Econométricos y Práctica Financiera. Revista Austriana de Economía, 221–252.

Engle, R. F. (1982). Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica, 50(4), 987–1007. https://doi.org/10.2307/1912773

Granger, C. W. J. (1969). Investigating Causal Relations by Econometric Models and Cross-spectral Methods. Econometrica, 37(3), 424–438. https://doi.org/10.2307/1912791

Nelson, D. B. (1991). Conditional Heteroskedasticity in Asset Returns: A New Approach. Econometrica, 59(2), 347–370. https://doi.org/10.2307/2938260

Newsham, G. R., & Birt, B. J. (2010). Building-level occupancy data to improve ARIMA-based electricity use forecasts. In Proceedings of the 2nd ACM Workshop on Embedded Sensing Systems for Energy-Efficiency in Building - BuildSys ’10 (p. 13). New York, New York, USA: ACM Press. https://doi.org/10.1145/1878431.1878435

Peramunetilleke, D., & Wong, R. K. (2002). Currency exchange rate forecasting from news headlines. Australian Computer Science Communications, 24(2), 131–139. https://doi.org/10.1145/563932.563921

Romero, M. C.,  Ramírez, E. & Lozano Reyes, F. (2007). La Tasa de Cambio: ¿Es Gerenciable? Estudios Gerenciales, 23(104), 131–156.

Toro, J., Garavito, A., López, D. C., & Montes, E. (2015). El choque petrolero y sus implicaciones en la economía colombiana. Borradores de Economía, 65.

Velásquez Henao, J. D., & Gonzáles Rivera, L. M. (2006). Modelado del índice de tipo de cambio real colombiano usando redes neuronales artificiales. Retrieved from http://www.scielo.org.co/pdf/cadm/v19n32/v19n32a13.pdf

Anexo 1. Correlograma de Residuos

En el correlograma se pueden observar los residuos del modelo verificando el valor p siendo en su totalidad superiores al 5%, lo que significa que los residuales del modelo son ruido blanco y no están correlacionados confirmado que el modelo está bien identificado.

 Fuente: Datos Extraídos de Bloomberg – Elaboración Propia.

Anexo 2. Correlograma de los residuos al cuadrado.

En el correlograma se pueden observar los residuos al cuadrado del modelo verificando el valor p siendo en su totalidad superiores al 5%, lo que significa que los residuales al cuadrado del modelo son ruido blanco y no están autocorrelacionados.

Fuente: Datos Extraídos de Bloomberg – Elaboración Propia.

1. Ingeniero Financiero – Trader Deuda Pública Colombia. Facultad de Ingenierías. Universidad de Medellín. Estudiante Maestría en Finanzas, e-mail: mariomartin88@hotmail.com

2. Magíster en Ciencias Estadísticas, Universidad Nacional, Estadística de la universidad Nacional. Docente tiempo completo Ingeniería Financiera e investigadora del Grupo de Investigaciones en Finanzas —GINIF— de la Universidad de Medellín, e-mail: dsguzman@udem.edu.co

3. Matemático de la Universidad de Antioquia, Magíster en Matemáticas Aplicadas de la Universidad EAFIT y Estudios de Especialización en Estadística de la Universidad Nacional sede Medellín. Docente tiempo completo Ingeniería Financiera e investigadora del Grupo de Investigaciones en Finanzas —GINIF— de la Universidad de Medellín, e-mail: foperez@udem.edu.co

4. Doctora en Economía (C), Universidad del Rosario; Magíster en Economía y Economista, Universidad de Antioquia. Docente tiempo completo Ingeniería Financiera e investigadora del Grupo de Investigaciones en Finanzas —GINIF— de la Universidad de Medellín. e-mail: njmarin@udem.edu.co