ISSN 0798 1015

Vol. 39 (Nº 06) Año 2018. Pág. 17

Modelos alométricos para estimativa da biomassa de fustes de árvores em floresta ombrófila densa no município de Portel no Estado do Pará-Brasil

Allometric models to estimate the biomass of boles of trees in tropical rain forest in the municipality of Portel in the State of Pará, Brazil

Cléo Gomes da MOTA 1; Marcos Ximenes PONTE 2; Daniela PAULETTO 3

Recibido: 29/09/2017 • Aprobado: 18/10/2017

Conteudo

1. Introdução

2. Metodologia

3. Resultados e discussão

4. Conclusões

Referências bibliográficas

1. Introdução

O manejo florestal é fundamental para a conservação das florestas levando em consideração a paisagem e a escala local, pois a atividade permite que populações nativas que usam as florestas e as preservam, obtenham benefícios econômicos e sociais, além dos benefícios ambientais da floresta em pé na Amazônia.  

A base para a realização de um bom manejo florestal é o inventário florestal, que consiste no levantamento das informações qualitativas e quantitativas dos recursos florestais da área objeto do manejo. Para quantificar o volume de uma árvore ou de uma população (floresta) é necessária a utilização de modelos precisos na determinação do estoque florestal (Mota e Silva, 2009).

Na Amazônia, os pioneiros no estudo da volumetria de florestas naturais foram Heinsdijk & Bastos (1963) que sugeriram o fator de forma médio 0,7 para as árvores da floresta Amazônica. Desde a década de 1960, várias pesquisas têm sido conduzidas sobre a quantificação dos estoques na Amazônia (Higuchi e Ramm 1985; Rolim, et al. 2006; Silva e Araujo, 1984; Silva, et al. 1984).

Entretanto, à constatação que as estimativas de volume (m3) dos inventários florestais para planos de manejo na Amazônia brasileira eram muito imprecisas fez com que os órgãos de licenciamento no Brasil passassem a exigir dos manejadores a utilização de equações de volume para cada área de manejo florestal (BRASIL, 2003).

A intensificação do debate sobre as florestas e as mudanças ocasionadas pelo uso do solo, levou à adoção de um novo modelo de gestão das florestas brasileiras, culminando no âmbito das florestas públicas do Brasil com a criação do Serviço Florestal Brasileiro (BRASIL, 2006), órgão responsável pela taxação do uso direto dos recursos florestais. Outro marco importante foi à reforma do código florestal brasileiro (BRASIL, 2012). Permitindo, que houvessem avanços tecnológicos como o uso de sistemas inteligentes para processar e modelar a realidade em três dimensões (3D) com extrema precisão por meio de aparelhos óticos que emitem nuvens de ponto que servem para obter medidas precisas através de sistemas laser (Lidar) utilizados para quantificar florestas inteiras e/ou árvores individuais.   

Entretanto, esses equipamentos ainda são muito caros, inacessíveis ao pequeno e médio detentor de floresta, que busca no manejo florestal uma alternativa de renda na Amazônia. Portanto, o uso de técnicas de mensuração direta e indireta, com maior rigor e rapidez ainda  são alternativas necessárias para obter modelos precisos e com baixo custo através do uso de equações alométricas.

Desta forma, o objetivo deste trabalho foi testar modelos de estimativa de volume da biomassa de fustes de espécies comerciais, em área sob manejo florestal da Fazenda Santa Catarina, Rio Pracupi afluente do rio Anapú, município de Portel, Estado do Pará.

2.1. Região de estudo

A região estudada faz parte da área do Plano de Manejo Florestal Sustentável (PMFS) da Fazenda Santa Catarina com cerca de 16.000 ha, localizada na bacia do rio Parcupi em área de Floresta Ombrófila Densa (FOD) na planície Amazônica no Município de Portel. A Unidade de Produção Anual (UPA) no ano de 2003 foi de 3.500 ha. Esta área foi dividida em 35 unidades de mapeamento denominadas de Unidade de Trabalho (UT) com 100 ha cada, que foram subdivididas em subunidades de 6,25 ha. Nesta UPA foram sorteadas 08 UT, em cada UT, foram selecionados dois mapas de exploração com extensão de 250 x 250 metros (6,25 hectares). Tendo como referência espacial a área destes mapas foram mensuradas todas as árvores abatidas naquela extensão totalizando 500 árvores. A área mensurada correspondeu a 5 % da área total da UPA.

Figura 1
Mapa de localização da área de estudo na Fazenda Santa Catarina, Rio Pracupi, Município de Portel – Pará - Brasil

2.2. Base de dados

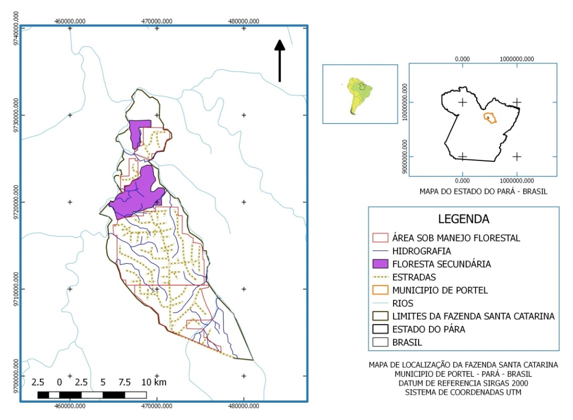
Para determinação da biomassa dos fustes foi realizada a cubagem rigorosa de 499 fustes de árvores abatidas durante a exploração florestal. O método empregado para a mensuração do volume da biomassa de fustes foi adaptado do método Smallian, adotado devido à sua fácil aplicabilidade em campo. A fórmula de Smallian calcula o volume com base na medição dos diâmetros internos. Para tanto foram medidas as circunferências das seções dos fustes das árvores abatidas com diâmetro à altura do peito (DAP) igual ou maior a 50 cm que foi o diâmetro mínimo de corte (Figura 2).      

Figura 2
Esquema de treinamento da coleta de dados de comprimento e circunferência
das seções do fuste após abate para cálculo de volume real (Procedimento de Smalian)
(Fonte: o autor).

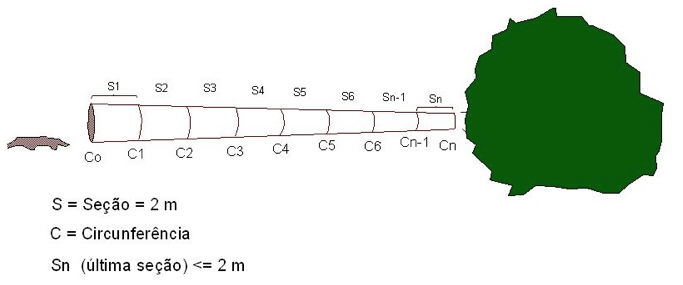
O volume total (m3) foi obtido pelo somatório do volume das seções individualmente conforme equação 01, adaptada do modelo de Smalian (Silva, et al., 1984; Scolforo, et al., 1998). Ou seja, após obter gi foi calculado a ATM entre o maior e menor diâmetro da tora (g1 e g2) em metro quadrado (m2) com casca. Esta porção foi multiplicada pelo comprimento da peça em metro linear (m) para encontrar o volume da peça, conforme equação abaixo:

                                             Equação 1

O Fator de forma (ff) foi obtido como pela relação do volume geométrico do cilindro, cuja definição se dá pelo DAP e pela altura total ou comercial das árvores e o volume real (Equação 2) obtido através da mensuração rigorosa realizada conforme o método Smalian. O ff também é chamado de fator de forma artificial, com base no volume com casca e o volume de um cilindro de diâmetro igual ao DAP com casca, e, de fatores de forma naturais baseados, por exemplo, no cilindro com diâmetro igual ao do meio da árvore, ou em alguma outra proporção da altura total. O método de Hohenadl, usado na Alemanha, é baseado no diâmetro a 1/10 da altura (GARCIA, 2004; SCOLFORO et al., 1993).

                                                   Equação 2

O ff é útil para estimativas de volume de modo expedito, ou seja, assumindo um fator de forma constante para espécies individualmente ou grupo de espécies no sitio, usando o ff para obter o volume estimado partir do geométrico conforme modelo de número treze (13) da tabela 1.

Os algoritmos mais utilizados na determinação do volume incluem análise de regressão linear, não linear, múltipla (Barros, et al., 2009; Chichorro, et al., 2003; Higushi, et al., 2004; Fernandes, et al., 2017) vizinho mais próximo e recentemente, também, redes neurais artificiais (Binoti, et al., 2014; Görgens, 2009; Cosenza, et al., 2015). Entretanto, a análise de regressão múltipla ainda é a abordagem mais utilizada para desenvolver modelos de estimativa de biomassa (Fernandes, et al., 2017; Higushi, et al., 1985; Grabill, 1976; Higushi, et al., 2004). Desta forma, para tomada de decisão do modelo de interpolação a ser usado para a estimativa de volume comercial (m3) do plano de manejo florestal foram avaliados diferentes modelos através da analise de regressão linear, não linear e múltipla (Tabela 1) utilizando diferentes formas funcionais indicados pela literatura (Barros, et al., 2009; Fernandes, et al., 2017; Higushi, et al., 1985; LU, et al., 2012; Silva, et al., 1984; Calkins, 2005).  

Tabela 1
Modelos alométricos indicados para estimativa de volume de fustes com diferentes formas funcionais
(linear, inversa, log-log, log-linear, linear-log - semi-log e log inversa)

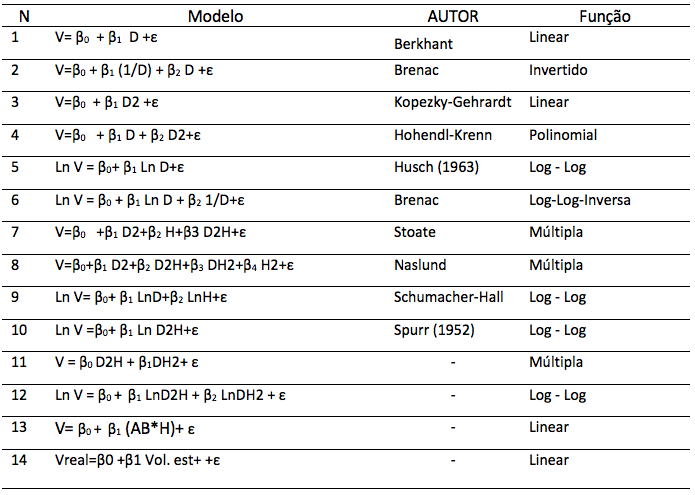
A análise de correlação (r) e o coeficiente de determinação (R2) foram obtidas com o uso das formulas abaixo, onde r é um número entre -1 a 1 e R2 assume valores que vão de 0 a 1 (Equações 3 e 4).

                                                       Equação 3

                                                             Equação 4

O coeficiente de determinação ajustado (R2a) mediu a força de associação linear entre x e y, considera o número de variáveis independentes inclusas na equação de regressão e o tamanho da amostra. É importante para avaliar equações com diferentes números de variáveis, diferentes números de amostras ou ambos (Hair Jr, et al., 2009).

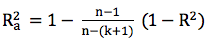                                                     Equação 5

O desvio padrão da regressão (sy.x) serve para  eliminar os efeitos dos quadrados existente na variância, bastando para isso extrair a raiz quadrada (Equação 6).

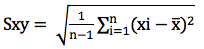                                                      Equação 6

Para a comparação de modelos lineares e modelos com transformação logarítmica foi feita  correção da discrepância logarítmica através do Fator de Correção de Meyer (1944). O Fator de Correção de Meyer consiste na elevação da base do logaritmo (2,71828182845904) a metade do desvio padrão conforme formula abaixo:

                                                                       Equação 7

O teste F foi utilizado para um conjunto de hipóteses conforme recomendado por Hill et al. (2010) para comparação da soma dos quadrados dos erros do modelo de regressão múltipla não restrita, com a soma dos quadrados dos erros de um modelo de regressão em que se supõem verdadeira a hipótese nula, ou seja, não há diferença entre os erros. O volume obtido com o uso das variáveis mensuradas e as formas funcionais selecionadas, depois de aplicado a análise de variância, serve para verificar se existem diferenças entre observado e o predito pelos modelos selecionados (Graybill, 1976; Hair Jr, et al., 2009; Hill, et al., 2010). Neste modelo a equação de regressão foi ajustada pelo volume real (Vreal) onde o volume estimado é a variável independente do volume real, conforme modelo 14 da tabela 1.

A hipótese nula é que b0=0 e b1=1, ou seja, o intercepto é igual a zero e a inclinação é igual a 1, contra a hipótese alternativa de rejeição de H0. O valor de F calculado foi comparado com um F tabelado (a; p; n-p), com um nível de probabilidade alpha de 0,05 com dois parâmetros do modelo e n-2 graus de liberdade. Se F calculado for menor que o tabelado, aceita H0, pois a estimativa obtida no modelo é igual ao volume real  (Chichorro, et al., 2003; Grabill, 1976; Hill, et al., 2010).

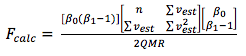                                        Equação 8

Além dos critérios descritos foi considerada também uma boa distribuição dos resíduos padronizados (Fernandes, et al. 2017, Higuchi e Ramm 1985, Barros e Silva Júnior 2009, Silva, et al. 1984, Rolim, et al. 2006), através da analise gráfica, que permite a identificação visual do comportamento dos resíduos da regressão e indícios de violação dos pressupostos básicos da analise de regressão.

Para tabulação dos dados foi utilizado à planilha EXCELL e para análise estatística foram utilizados os softwares STATISTICA e R.     

A amostragem obtida nas 500 árvores abrangeu 25 famílias botânicas distribuídas em 41 espécies (Figura 3). As espécies mais frequentes foram: maçaranduba (Manilkara sp.), tauari (Couratari spp.), andiroba (Carapa guianensis Aubl.), ucuubarana (virola sp.) e cupiuba (Goupia glabra Aubl.), que representaram 50% das espécies mensuradas na amostra.

Figura 3 - Relação de famílias e quantidade de espécies mensuradas na área de Floresta da Fazenda Santa Catarina, rio Pracuru,  Município de Portel-PA (Fonte: O autor).

Este grupo de espécies, quando comparado com os dados de riqueza de espécies obtidos em inventário florestal realizado nesta mesma população, representou apenas 21% (41 de 197 espécies arbóreas) de todas as espécies arbóreas encontradas no inventário amostral da área de manejo. Nesta região do estudo as 41 espécies faziam parte do grupo de mais de 60 espécies exploradas para atender o mercado de madeiras de diferente densidade na safra de 2003/2004.

Em região próxima, na mesma bacia hidrográfica, na margem direita (oposta) do rio Anapú, foram desenvolvidos estudos similares para estimativa de volume comercial de madeira em floresta nativa. Um destes trabalhos, desenvolvido por Barros e Silva Júnior (2009) no interflúvio dos rios Anapú e o rio Pacajá, mensurou 212 indivíduos de 33 espécies. Neste mesmo município, em empreendimento florestal comunitário do Projeto de Desenvolvimento Sustentável Virola-Jatobá foram mensuradas 132 árvores em 25 espécies (Barreto, et al. 2014). Essa diferença na variedade e quantidade de espécies mensuradas, de modo geral, depende das características do sitio explorado, das espécies existentes, da demanda do mercado para o ano em questão, além de capital, disponibilidade de recursos humanos capacitados, materiais, maquinários e de florestas para colheitas futuras.

Na tabela 2 são apresentados os resultados da estatística descritiva das variáveis mensuradas: diâmetro (DAP), altura (H) e fator de forma (FF) e Área Basal (AB) em relação ao volume real da biomassa (Vreal ) das amostras de 500 fustes. Nesta são apresentadas a média, o valor mínimo e máximo e o desvio padrão (SD) da variável mensurada.

Tabela 2
Estatística descritiva (média, mínimo, máximo e desvio padrão) da variável dependente volume (VOL) e as variáveis independentes diâmetro à altura do peito (DAP), Altura do fuste (Hf) e fator de forma (FF), Área basal (AB) para 500 amostras na área de Floresta da Fazenda Santa Catarina, rio Pracuru, ME do rio Anapú, Município de Portel-PA.

O volume médio dos fustes para foi de 7,78 m3 com desvio padrão de 4,16 m3 (mínimo 2,28 m3 e máximo 30,34 m3). A variável DAP teve média de 0,83 m com desvio padrão (DP) 0,18 m com valor de DAP mínimo e máximo de 0.51 - 1.64 m. A área basal (AB) teve média de 0,57 m2 com mínimo e máximo entre 0,21 - 2,11 m2 e DP de 0,28 m2. A variável altura do fuste (Hf) teve média de 19,39 m com DP de 4.25 m e altura mínima e máxima de 4.61 - 34.60 m. O fator de forma médio foi de 0,705 com DP de 0,08 com mínimo e máximo de 0,50 - 1,27.

O fator de forma obtido neste estudo não diferiu o encontrado por Heinsdijk, et al (1963) de 0,7 amplamente usado na Amazônia. Este quociente de forma é amplamente usado na América do Norte, na Europa Central (GARCÍA, 1995) e nas regiões tropicais para serem usados em modelos de volume tanto para espécies como para populações (HEINSDIJK, et al., 1963; Scolforo, et al., 1998; GARCÍA, 1995).

A seguir, na tabela 3, são apresentados os resultados obtidos pelas estatísticas utilizadas para seleção do modelo com melhor ajustamento à reta de regressão dos coeficientes (βn) das equações, erro padrão dos estimadores (SE β), estatística t (Student) e nível de probabilidade (p-valor). Além do desvio padrão (SD), fator de correção de Mayer (FCM) para a comparação entre o SD dos modelos com variáveis diretas e variáveis transformadas, coeficiente de determinação ajustado (R2a) e  teste  F, aplicados ao modelo de regressão.

Tabela 3
Resumo dos resultados dos estimadores (β), Erro padrão (SE β), estatística t, nível de probabilidade (p), desvio padrão da regressão (DPReg), índice de determinação ajustado (R2a),  teste  F, o índice de Furnival e Fator de correção de Mayer (FCM) para a área de Manejo Florestal da Fazenda Santa Catarina, ME do rio Anapú, Município de Portel-PA.

Fonte: o autor
** Indica altamente significativo a nível de  ρ <0,05.

O teste t aplicado para medir a variância do erro das estimativas da amostra em relação ao volume real observado (ß0 e ß1 representam estatísticas da amostra) obteve valor altamente significativo a 5% de probabilidade para o estimador do intercepto nos modelos 1, 2, 4, 5, 6, 7 e 11, indicando que as variáveis independentes utilizadas apresentaram efeito significativo no intercepto, Os modelos 3, 8, 9, 10 e 12 não apresentaram efeito significativo na estimativa do intercepto, indicando que este não apresentou diferença significativa de zero (0), ao nível de probabilidade de alpha de 5%, podendo ser excluído do modelo, Entretanto, todos os modelos foram submetidos ao teste F e, obtiveram valor altamente significativo, a 5% de probabilidade de alpha.

Os modelos de simples entrada com uso da variável diâmetro apresentaram pouca variação entre os resultados estatísticos nos modelos testados (modelos 1 a 6). Em relação à qualidade do ajustamento (R2a) estes modelos obtiveram poder explicativo da variância existente variando de 78% a de 81%, a 5% de probabilidade de alpha. O desvio padrão (DP) variou de 1,26 m3 (modelo com variáveis transformadas) a 1,36 m3  (modelos sem variáveis transformada).   

Dentre os modelos de dupla entrada, os modelos 7, 8 e 11, que não foram utilizadas variáveis transformadas pelo logaritmo, obtiveram poder de explicação da variância de 95% para os modelos 7 e 11 e 96% para o modelo 8. Os valores de desvio padrão da média foi igual para os modelos 7 e 8  (DP: 0,93 m3) e um pouco menor para o modelo 11 que obteve DP de 0,92 m3.

Os modelos 9, 10 e 12 com variáveis transformadas pelas funções logarítmicas, tanto para a variável dependente como para as variáveis explicativas (diâmetro e a altura) obtiveram poder de explicação da variância por R2 ajustado de 95%, 94% e 95%, respectivamente, para estes modelos. O DP ajustado pelo FCM para estes três modelos foi de 1,17, 1,18 e 1,7 m3, respectivamente.

O modelo 13 que utilizou o fator de forma da amostra que foi de 0,7055, aproximadamente o mesmo obtido por Heinsdijk, et al (1963) obteve desvio padrão de 0,97 m3 com poder de explicação de 95% da variância obtida pelo valor de R2 ajustado e F calculado altamente significativo de       9033,2.

A análise gráfica dos resíduos em relação ao volume previsto para os modelos 1 a 4 indicaram a existência de tendenciosidade na estimativa (Figura 5 e 6), pois a distribuição dos resíduos e a variância do erro não se apresentaram constantes ao longo da reta, crescendo com o aumento de volume previsto, sugerindo a possível violação da regra da homocedasticidade nestes modelos. Neste caso, a alternativa foi testar modelos com transformação das variáveis para obter melhores estimadores não viesados conforme proposto por Parresol (1999) e Hill et al. (2010).

Figura 5
Gráfico dos desvios dos volumes estimados pelos modelos de simples entrada
(A -Berkhant e B – Brenac) para determinação de volume na área da Fazenda Santa Catarina,
Rio Pracupi, Afluente da margem esquerda do Rio Anapú no Município de Portel – Pará - Brasil.

-----

Figura 6
Gráfica dos desvios, em relação ao volume estimado, pelos modelos de simples entrada
(A - Kopezky-Gehrardt e B – Hohendl-Krenn) para a área de manejo da Fazenda Santa Catarina,
Rio Pracupi, Afluente da margem esquerda do Rio Anapú no Município de Portel – Pará - Brasil.

Nas figuras 7 A e B temos as análise gráfica dos resíduos dos modelos 5 e 6, que corroboraram a expectativa de uma melhor distribuição dos resíduos em relação aos modelos anteriores sem transformação logarítmica das variáveis.

Figura 7
Gráfica dos desvios em relação ao volume estimado pelos modelos de simples entrada
(A - Modelo de Husch e B – Modelo de Brenac) com variável transformada (logaritmo)
para área de manejo florestal da Fazenda Santa Catarina, Rio Pracupi, Afluente da
margem esquerda do Rio Anapú no Município de Portel – Pará - Brasil.

Na figura 8 (A e B), podemos observar que estes modelos apresentam padrão semelhante que indicam tendenciosidade, visto que as distribuições dos resíduos possuem mesmo padrão para a variância do erro, que não se apresentam constante ao longo da reta, ou seja, a dispersão do erro cresce com o aumento do volume previsto em relação ao volume real observado.

Figura 8
Gráficos dos desvios em reação ao volume estimado pelos modelos volumétricos de dupla entrada
(A - Modelo de Stoate e B - Modelo de Naslund) para a área da Fazenda Santa Catarina, Rio Pracupi,
Afluente da margem esquerda do Rio Anapú no Município de Portel – Pará - Brasil.

Os modelos 9 e 10 possuem tanto a variável dependente (volume) como as variáveis explicativas (diâmetro e a altura) transformadas pela função logarítmica. De modo análogo aos modelos 5 e 6, a análise gráfica dos resíduos demostrou que os modelos (9 e 10) apresentam melhor distribuição dos resíduos. Tendo o modelo de Schumacher-Hall (9) apresentado visualmente uma melhor dispersão do erro que o modelo 10 de Spurr (figura 9).  

Figura 9
Gráficos dos desvios em relação ao volume estimado por modelos volumétricos
de dupla entrada com variável transformada (A - Modelo de Schumacher-Hall e B - Modelo de Spurr)
para área da Fazenda Santa Catarina, Rio Pracupi, Afluente da margem esquerda do
Rio Anapú no Município de Portel – Pará - Brasil.

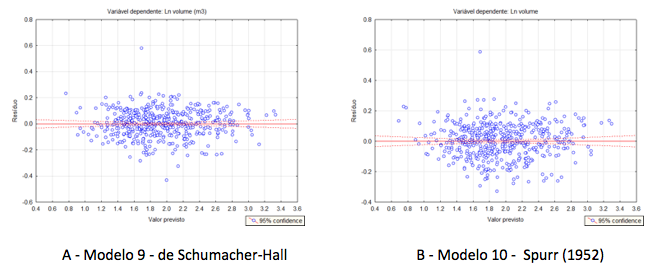
Entre os modelos 11 e 12, a análise gráfica dos erros comprovam a eficiência do uso da transformação das variáveis pelo logaritmo para ajustamento dos modelos (Figura 10).   No modelo 12 o ajustamento dos desvios ao longo da reta de regressão indicam uma distribuição mais uniforme, semelhante aos outros modelos com uso de variável transformada pelo logaritmo.

Figura 10
Gráficos dos desvios em relação ao volume estimado por modelos volumétricos
de dupla entrada A e B com variável transformada para área da Fazenda Santa Catarina,
Rio Pracupi, Afluente da margem esquerda do Rio Anapú no Município de Portel – Pará - Brasil.

Todos os modelos testados são frequentemente citados como adequados para a Floresta Amazônica, tanto para equações genéricas utilizadas para grupos de espécies (Colpini et al., 2009; Rolim et al., 2006; Thaines et al., 2010; Borges, 2015; Silva, et al., 2014) quanto para estimativa de volume por espécie (Moura, 1994; Ribeiro et al., 2014; Cysneiro, et al. 2017). Além do que são também frequentemente usadas para a determinação da dinâmica de biomassa e carbono em florestas na Amazônia Central (Higushi, et al., 2004).

Resultados semelhantes aos encontrados neste estudo foram observados por Silva et al., (1984); Barros et al., (2009); Rolim (2006); Silva, et al., (2014) que obtiveram maior precisão e melhor ajustamento com uso de modelos logarítmicos em florestas nativas na região Amazônica. 

Os modelos de simples entrada testados, de modo geral, apresentaram coeficiente de determinação ajustado elevado, porém foram rejeitados devido a sua elevada tendenciosidade principalmente para os fustes mais volumosos e o menor poder explicativo desses modelos. Por outro lado, o modelo de simples entrada, com variável transformada pela função logaritmo, foi considerado por Barros (2009) indicado para estimativa do volume das árvores em pé no Município de Anapú, em região próxima a área de estudo, entretanto na porção oposta na bacia hidrográfica do rio Anapú. Nesta mesma região, numa área de empreendimento florestal comunitário do Projeto de Desenvolvimento Sustentável Virola-Jatobá, o modelo de Husch, com variável transformada pela função logaritmo, foi considerado adequado para estimar o volume. Porém, os autores indicaram estes modelos pela precisão aceitável e possibilidade de redução de custo e do tempo na realização de inventários em campo (Barreto, et al. 2014).

O modelo 13 que utilizou o fator de forma 0,7, encontrado na amostra e aplicado ao volume geométrico para a determinação do volume apresentou resultados estatísticos que o habilita para uso na estimativa do volume nesta população estudada, pois teve elevado poder de explicação (R2a: 0,95) e baixo desvio padrão (DP: 0,97 m3).

Na figura 11 são plotadas as estatísticas básicas (gráfico boxplot) para comparação dos resultados da média, desvio padrão e intervalo de confiança, representado pela média mais ou menos 1,96 vezes o Erro Padrão [4], para os modelos 2, 9, 7, 11, 12 e 13 em comparação ao resultado do volume observado (VOL).

Figura 11
Gráfico do intervalo de confiança entre os modelos 2, 7, 9, 11, 12 e 13 previamente
selecionados para estimativa de volume na área da Fazenda Santa Catarina, Rio Pracupi,
afluente da margem esquerda do Rio Anapú no Município de Portel – Pará - Brasil.

O gráfico da figura 11 demostra que os modelos 2, 7, 11 e 13, possuem menor variação do erro em relação à média. Apesar de todos os modelos apresentarem resultados que os validadam na determinação do volume, tendo os modelos 7, 11 e 13 apresentaram graficamente comportamento semelhante entre o volume observado na amostra e o estimado por estes modelos. Nesta analise pode-se observar que o efeito da transformação das variáveis pela função logaritmo, como os modelos de Schumacher-Hall (9) e o modelo 12. Porém, induzem a uma subestimativa de volume, principalmente para os indivíduos de menor volume que são mais numerosos na amostra e consequentemente na população. 

Os modelos testados para determinação do volume de fustes apresentaram bom ajustamento com elevado poder de explicação e baixo desvio padrão da estimativa. Entretanto, os modelos de dupla entrada com uso das variáveis diâmetro e altura, destacaram-se dos demais modelos estudados, pois obtiveram os melhores ajustamentos aos parâmetros utilizados na analise. Vale destacar que, a transformação das variáveis utilizando a função logaritmo produziu o efeito desejado na redução da heterodasticidade, obtendo melhor distribuição dos resíduos ao longo da reta de regressão. Porém, induziram a uma subestimativa do volume, principalmente para os indivíduos com menor volume, que foram mais numerosos na amostra da população.  Desta forma, o modelo selecionado foi o modelo 11, que apresentou maior poder de explicação, menor desvio padrão da estimativa e valor de F altamente significativo (V = 0,4261 + 0,6142 D2H -0,0040DH2).

Barreto, W. F., F. M. Leão, M. C. Menezes, e D. V. Souza. (2014). Equação de volume para apoio ao manejo comunitário de empreendimento florestal em Anapu, Pará. Pesquisa Florestal Brasileira, 12 (1).

Barros, P. L. C. de e Silva Júnior, A. T. da. (2009). Equação de volume para árvores de uma floresta tropical densa no município de Anapu, Oeste do estado do Pará, Amazônia oriental. Rev. ciências agrárias. (51), pp. 115-126.

Binoti, M. L. M. da S.; Binoti, D. H. B.; Leite, H. G.; Lage, S.; Garcia, R.; Ferreira, M. Z.; Rode,  R.; Silva,  A. A. L. da. (2014). Redes neurais artificiais para estimação do volume de árvores. Revista Árvore, 38(2), p.283-288.

Borsoi, G. A, B.V Müller, Doádi, e A. B. Equações de volume para galhos de espécies em diferentes grupos de valor econômico em uma Floresta Ombrófila Mista. Ambiência Guarapuava, (set./dez), pp. 869 - 878.

Cabacinha, C. D.; Scolforo, J. R. S.; Thiersch, C. R.; Sales,  N. DE L. P., e Carvalho, L. R. DE.. (2013). Uma nova abordagem para o método geométrico usando o índice da parábola. Ciência Florestal, (01), pp. 261-271.

Chichorro, J. F., Resende, J. L. P. e Leite, H. G. (2003). Equações de volume e de taper para quantificar multiprodutos da madeira em floresta Atlântica. Revista Árvore. 27(6).

Cysneiro, V. C.; Pelissari, A. L.; Machado, S. do A. ; Filho,A. F. e Souza, L.. (2017). Modelos genéricos e específicos para estimativa do volume comercial em uma floresta sob concessão na Amazônia. Scientia Forestalis, (6) p114.

Colpini, C.; Travagin, D. P.; Soares, T. S.; Silva, V. S. M. (2009). Determinação do volume, do fator de forma e da porcentagem de casca de árvores individuais em uma Floresta Ombrófila Aberta na região noroeste de Mato Grosso. Acta Amazonica, 39(1), pp.97-104.

Cosenza, D. N.; Leite, H. G.; Marcatti, G. E.; Binoti, D. H. B.; Alcantra, A. E. M.; Rode, R. (2015). Classificação da capacidade produtiva de sítios florestais utilizando máquina de vetor de suporte e rede neural artificial . Scientia Forestalis, 43(108), pp.955-963.

Durbin, J. e Watson, G. S. (1951). Testing for serial correlation in least squares regression. Biometrika, 38 (1-2) pp. 159-178. (10.1093/biomet/38.1-2.159. 1-2, 1951).

Fernandes, A. M. V., et al. (2017). Equações volumétricas para Carapa guianensis Aubl. e Swietenia macrophylla King em sistema silvipastoril na Amazônia. Revista Nativa. 1(5), pp. 73-77.

García, O. (1995). Forest Mensuration. Monografia, September 1995. Santiago: Universidad Austral de Chile Faculty of Forestry Sciences Institute of Forest Management.

Graybill, F.A. (1976). Theory and application of the linear model. Massachusetts : Duxbury Press,  p. 704.

Görgens, E. B. et al. Estimação do volume de árvores utilizando redes neurais artificiais. Revista Árvore, 33(6), p.1141-1147.

Grosenbaugh, L. R. (1966).Tree form: deninition, interpolation, extrapolation. Conference on Wood Mesurement. Port Arthur-Ontario-Canada.

Heinsdijk, D. e Bastos, A. M. (1963). Inventários florestais na Amazônia. Rio de Janeiro : Ministérioda Agricultura, . 100p.

Higuchi, N. e Ramm, W. (1985). Developing bole wood volume equations for a group of tree species of central Amazon (Brazil). The Commonwealth Forestry Review. 64(1), pp. 33-41.

Higuchi, N., et al. (2004). Dinâmica e balanço do carbono da vegetação primária da Amazônia central. Floresta. (34), pp. 295-304.

HILL, R. C., JUDGE, G. G. e GRIFFITHS, W. E. (2010). Econometria. São Paulo : Saraiva,. 469p.

Lu, D., et al. (2012). Aboveground Forest Biomass Estimation with Landsat and LiDAR Data and Uncertainty Analysis of the Estimates. International Journal of Forestry Research.  pp. 1-16.

Mota, C. Gomes da; e Silva, J. N. S. (2009). Determinação da equação de volume para árvores e para toras na área de Manejo Florestal da fazenda Santa Catarina, rio Anapú, município de Portel, Pará. In: Livro de resumos da 59 reunião da sociedade brasileira para o progresso da ciência (SBPC),  SBPC. Belém, Pará.

Oliveira, M. L. R., H. G. Leite, S. L. R. Garcia, J. C. C. Campos, C. P. B. Soares, e R. C. Santana. (2009). Estimação do volume de árvores de clones de eucalipto pelo método da similaridade de perfis. Revista Arvore, 1(2).

Parresol, B.R. (1999). Assessing Tree and Stand Biomass: A Review with Examples and Critical Comparisons. Forest Science, (45) pp. 573.593.

Rolim, S. G., et al. (2006). Modelos volumétricos para a Floresta Nacional do Taipé-Aquirí, Serra dos Carajás. Acta Amazonica.  36(1), pp. 106-114.

Scolforo, J.R.S. e Figueiredo Filho, A. (1998). Biometria Florestal: medição e volumetria de árvores. Lavras : UFLA/FAEPE, 310p.

Silva, J. N. M., J. O. P. DE Carvalho, J. do C. A. Lopes, e M. S. P. DE Carvalho. (1984). Equações de volume para a Floresta Nacional do Tapajós (Volume Equations For The Tapajós National Forest). Boletim de Pesquisa Florestal, 6 (0)pp.50-63.

Spurr, S. A. (1962). Measure of point density. For. Sci. 8(1), pp. 85-96.

Thaines, F.; Braz, E. M.; Mattos, P. P.; Thaines, A. A. R. (2010). Equações para estimativa do volume de madeira para a região da bacia do Rio Ituxi, Lábrea, AM. Pesquisa Florestal Brasileira, 30(64), p. 283-289.

1. Instituto Socioambiental Floranativa. Coordenação Técnica. MSc. Em Agronomia, Doutorando do curso de pós-graduação Sociedade Natureza e Meio Ambiente da Universidade Federal do Oeste do Pará. e-mail coodenacaotecnicaphv@gmail.com

2. Instituto de Tecnologia. Universidade Federal do Pará. Prof. Dr. em  Engenharia Mecânica. ximenes@ufpa.br

3. Instituto de Biodiversidade e Florestas. Universidade Federal do Oeste do Pará. MSc. Ciências Florestais

4. Intervalo de confiança no qual 95% da variação encontra-se dentro do limite estabelecido