

Vol. 39 (Nº 04) Año 2018. Pág. 42
Mónica Andrea ARANGO Arango 1; Sebastián ALZATE López 2; Diana Sirley GUZMÁN Aguilar 3
Recibido: 04/08/2017 • Aprobado: 01/10/2017
2. El concepto fundamental del criterio de Kelly
RESUMEN: El objetivo principal de un inversionista a la hora de conformar un portafoliode acciones, es obtener una ganancia sobre el capital invertido a la vez que distribuye el riesgo. El método más popular hasta el momento para hacer esto es el de Markowitz (Markowitz, 1959), el cual minimiza la varianza del portafolio para un valor fijo de retorno esperado. En este trabajo se presenta el criterio de Kelly como alternativa a la de Markowitz con el fin de maximizar la rentabilidad esperada y se muestra el proceso para estimar un portafolio bajo esta metodología, utilizando los datos de las acciones del índice COLCAP de la bolsa de valores de Colombia. En este caso se encontró que el criterio de Kelly arrojó un portafolio muy poco diversificado y con pocas acciones, que generó un retorno mayor a la de la estrategia pasiva de invertir en el índice COLCAP. |
ABSTRACT: The main objective of an investor when forming a portfolio of shares, is to obtain a return on the invested capital while distributing the risk. The most popular method so far to do this is the one proposed by Markowitz (Markowitz, 1959), which minimizes the variance of the portfolio for a fixed value of expected return. In this paper, the Kelly criterion is presented as an alternative to Markowitz's in order to maximize the expected return. The process for estimating a portfolio under this methodology is shown using the data of the COLCAP index from the Colombian stock exchange. In this case, it was found that the Kelly criterion gave a much less diversified portfolio with few shares, which generated a greater return than the passive strategy of investing in the COLCAP index. |
En el mercado accionario, el objetivo de todo inversionista es obtener una ganancia como resultado de una operación de compra o venta de una o varias acciones, por lo tanto, su decisión de compra o venta siempre estará basada en las predicciones que tenga acerca de la dirección que va a tomar el precio de la acción (Fama, 1965). De allí que, los inversionistas que participan en este mercado compran acciones cuando sus predicciones son alcistas, y venden las que ya poseen cuando sus predicciones apuntan a una caída del precio, por lo tanto, el análisis de las ventas en corto dentro de cualquier modelo o estrategia está fuera de los intereses de este trabajo. Para predecir el rumbo de los precios de las acciones, los inversionistas utilizan diferentes teorías y estrategias como el análisis fundamental, el análisis técnico y combinaciones entre estas dos.
Una estrategia importante en la negociación de acciones es el Position Sizing o distribución del capital, el cual se puede interpretar como la administración del dinero y consiste en seleccionar de forma óptima, la cantidad del capital disponible a invertir en una acción individual, o en un grupo de acciones que conforman un portafolio. Por medio de la administración del dinero, un inversionista puede determinar el factor de apalancamiento óptimo en cada negociación y así maximizar la rentabilidad de su inversión (Sewell, 2011). Aunque este tamaño de la posición afecta crucialmente las características de riesgo y rentabilidad, la literatura académica reciente ha ignorado este efecto, dejando resultados reportados incomparables, perdiendo de vista un factor importante y corriendo el riesgo de malinterpretar o no entender completamente los resultados empíricos (Scholz, 2012).
La forma más común de distribuir el capital en un portafolio es usar la teoría de portafolio de varianza media de Markowitz (Markowitz, 1959), quien reconoció el riesgo de los portafolios y lo cuantificó en términos de varianza, introduciendo así la noción del portafolio eficiente AM-V, el cual minimiza la varianza del portafolio para cualquier valor fijo de retorno esperado. La teoría general de varianza media no se ocupa de la capitalización de la inversión, pero la teoría realista relacionada con las inversiones, en la mayoría de los casos no puede hacer frente a la reinversión, ya que la riqueza acumulada, producto de la reinversión de las ganancias, es inimaginablemente más alta que en otros casos.
Así que, para maximizar el retorno compuesto en el largo plazo, se debe construir un portafolio con una media geométrica optimizada en lugar de una media aritmética, este es el propósito del criterio de Kelly (Kelly, 1956). El cual sirve como un método para estimar el Position Sizing, ya que maximiza el valor esperado de la función de utilidad (Hung, 2010).
Dadas las características del criterio de Kelly, este trabajo es de importancia para los administradores de portafolio, académicos e inversionistas, púes da herramientas adicionales y diferentes a las utilizadas comúnmente en la selección de portafolios. Por esto, se muestra la metodología, y se explica el desarrollo completo, iniciando con la selección de los datos, cálculos iniciales necesarios, y el manejo de esta información para la estimación final del portafolio.
Este trabajo está dividido en 4 secciones, en la sección 1 se realiza una revisión de la literatura, donde se hace un recorrido por los autores que han hecho aportes y modificaciones al criterio de Kelly, en la sección 2, se explican los conceptos fundamentales del criterio de Kelly y se desarrolla la adaptación de la metodología al mercado de capitales. En el inicio de la sección 3, se muestra el proceso realizado para estimar un portafolio por medio del criterio de Kelly utilizando acciones del mercado colombiano, y después se comparan los resultados obtenidos con el desempeño del índice COLCAP. Por último, se presentan las conclusiones en la sección 4.
A continuación, se hace un recorrido por los trabajos que han hecho aportes y modificaciones al criterio de Kelly, presentando los autores más importantes para el desarrollo de la metodología y dando a conocer sus opiniones, positivas o negativas, acerca de su utilidad.
Thorp (Thorp, 1969) muestra las ventajas de maximizar la tasa de crecimiento exponencial y relaciona por primera vez el criterio de Kelly con los mercados financieros, adaptándolo para la selección de portafolios y comentando que el criterio de Kelly puede proveer una teoría más ajustada que la de Markowitz (Markowitz, 1959), la cual ha sido el estándar de referencia para la selección de portafolios desde la presentación de su trabajo.
En contraste, autores más recientes parecen discrepar frente a esta crítica hacia Markowitz, Laureti, Medo y Zhang (Laureti, Medo, & Zhang, 2009) mencionan que la frontera eficiente de Markowitz es la línea en la que deben estar los portafolios eficientes en el gráfico de la varianza media, y después de derivar una formula analítica altamente acertada para hallar las fracciones óptimas de un portafolio, concluyen que la diferencia entre el enfoque del criterio de Kelly y el enfoque de la varianza media de Markowitz es muy pequeña y no justifica la complejidad adicional inducida. Kim y Suhee (Kim & Suhee, 2013) se adhieren al debate concluyendo que invertir en el mercado accionario usando el criterio de Kelly, da como resultado tasas de retorno mucho mayores en un portafolio que las estrategias de inversión tradicionales.
El Criterio de Kelly no ha perdido vigencia en el marco de las apuestas, Piotrowski y Schroeder (Piotrowski & Schroeder, 2007), usan simetrías descriptivas para explicar la maximización del logaritmo de la riqueza y obtienen una función de ganancias máximas, también ha sido utilizado por Hung (Hung, 2010) para determinar la fracción del capital a apostar en un juego por medio de simulaciones.
Edward Thorp sigue ampliando sus aportes en la selección de portafolio y el criterio de Kelly en trabajos posteriores (Rotando & Thorp, 1992; Thorp, MacLean, & Ziemba, 2010; Thorp, 1975, 1980, 2008), volviéndose un referente importante para el desarrollo y estudio del tema. En años más recientes, otros autores como Lv y Meister (Lv & Meister, 2010), Phataford (Phatarfod, 2012) y Kim y Suhee (Kim & Suhee, 2013) han seguido utilizando el criterio de Kelly para darle enfoques diferentes a la teoría de portafolios.
Subbiah y Fabozzi (Subbiah & Fabozzi, 2016) propusieron un modelo para construir un fondo asiático de fondos de cobertura, y encontraron que el criterio de Kelly, junto a una regresión de mínimos cuadrados ordinarios, una regresión no paramétrica y las variables del modelo de ocho factores de Fung-Hsieh, arrojó la tasa de información más alta para predecir los retornos de un fondo de cobertura y generar proyecciones. MacLean, Zhao y Ziemba (MacLean, Zhao, & Ziemba, 2016) proveen un método de control de riesgo que castiga con una función convexa, los déficits que caigan por debajo de la trayectoria de un VaR, causando una tasa de crecimiento más baja que la estrategia de Kelly, pero manteniendo bajo control el riesgo de perder.
Zambrano (Zambrano, 2014) hace una crítica al criterio de Kelly, argumentando que puede llevar a un inversionista a invertir una fracción mayor de su capital cuando enfrenta probabilidades menos favorables, motivándolo a arriesgar una gran proporción de su riqueza en el resultado de un solo evento. Zambrano no es el único que tiene resultados desalentadores, Phataford (Phatarfod, 2012) compara el sector de la banca y el mercado de capitales, y argumenta que si el administrador de un fondo adopta el criterio de Kelly, hay un límite superior para la volatilidad de éste, en el cual invertir en él no es tan rentable como poner el dinero en un banco, y Hung (Hung, 2010) menciona que aunque el criterio de Kelly es efectivo para encontrar la cantidad óptima del capital a apostar o invertir, éste debe ser alto para poder alcanzar ganancias sustanciales, por lo cual argumenta que el criterio es impráctico y no aplicable para muchas situaciones.
Zambrano (Zambrano, 2014) también comenta que la estrategia de Kelly ha desarrollado la reputación de ser parte de muchas estrategias exitosas en las cuales grandes inversionistas como Warren Buffet y Bill Gross, distribuyen su capital en formas que son consistentes con el criterio, y en años recientes se han desarrollado diferentes aplicaciones y enfoques basadas en el criterio de Kelly.
Lv y Meister (Lv & Meister, 2010) aseguran que si el mercado es completo, existe una estrategia óptima de autofinanciamiento, Lundström (Lundström, 2014) propone una estrategia de administración del dinero con la cual los inversionistas pueden incrementar la rentabilidad de sus negociaciones por encima de las existentes, Osorio (Osorio, 2009) deriva una aproximación para los niveles de apalancamiento como resultado de la optimización de la función de utilidad logarítmica asociada con el criterio de Kelly, y comenta que las distribuciones t-Student son buenas candidatas para verificar cómo se comporta el criterio con eventos extremos. Es importante recalcar que varios autores como Laureti (Laureti et al., 2009), Hung (Hung, 2010), Kim y Suhee (Kim & Suhee, 2013) y Lv y Meister (Lv & Meister, 2010) analizan la maximización logarítmica del capital.
El objetivo de cualquier inversionista siempre será obtener una ganancia o retorno sobre el capital invertido, y para esto siempre buscara opciones favorables, es decir, donde las probabilidades de ganar sean mayores a las de perder. Si el inversionista desea maximizar su ganancia esperada, debería invertir todo su capital en cada opción favorable que encuentre, pero esta estrategia lo dejaría en la ruina con una probabilidad del 100%, por lo tanto, la estrategia de maximizar la ganancia esperada es inútil.
Otro enfoque podría ser tratar de minimizar la probabilidad de quedar en la ruina, pero esto disminuiría significativamente la ganancia esperada, lo que convierte a las inversiones pequeñas en una apuesta poco atractiva. Entonces surge la pregunta: ¿Qué porcentaje del capital se debe invertir en cada opción favorable?
John Larry Kelly presentó en 1956 (Kelly, 1956) una teoría sobre ruidos en canales de comunicación que se puede extender para resolver este problema, y hoy en día se conoce como el criterio de Kelly.
El propósito principal del criterio de Kelly es permitirles a los inversionistas determinar el porcentaje del capital a apostar o invertir para maximizar la tasa de retorno logarítmica esperada en una inversión. Haciendo esto, los inversionistas podrían acumular una máxima cantidad de su riqueza.
Los planteamientos mostrados y discutidos en esta sección están basados principalmente en el trabajo de Thorp (Thorp, 1969, 2008) y Kim y Jung (Kim & Suhee, 2013; Osorio, 2009), el cual surgió de un importante intercambio académico con Gyutai Kim. Para comenzar a entender el proceso de derivación del criterio de Kelly es necesario tener en cuenta la siguiente ecuación:






Para realizar el proceso se seleccionó la canasta 32 del índice COLCAP, que estuvo vigente desde noviembre de 2015 hasta enero de 2016, y contiene 24 acciones de la Bolsa de Valores de Colombia (BVC). Se recolectaron los datos de precio de cierre ajustado diarios, en el periodo comprendido entre enero 5 de 2009 y noviembre 11 de 2015 por medio de la plataforma Bloomberg, con la intención de tener información de más de 5 años. En el Gráfico 1 se indica el proceso que se siguió para realizar la aplicación.
El COLCAP es un índice de capitalización que refleja las variaciones de los precios de las acciones más liquidas de la BVC, la canasta varía cada tres meses y su selección dependerá de los resultados arrojados por el cálculo de una función de selección, la cual determinará un valor que mide la liquidez para cada una de las acciones del mercado. En este caso, se seleccionó la canasta 32, ya que es la que estaba vigente en la fecha en la que se recolectaron los datos. En el Gráfico 2 se pueden observar las acciones contenidas en esta canasta y su ponderación.
Debido a que el mercado de acciones colombiano no es tan liquido en comparación con otros mercados más desarrollados, se presenta el caso en el que algunas acciones no se negocian en algunos días, por lo tanto, quedan fechas sin dato de precio de cierre, el cual es necesario en todas las fechas para poder realizar los cálculos pertinentes. Estos datos faltantes se suplieron de la siguiente forma: en los días en los que no hay información de precio de cierre, este valor se reemplazó con el precio de cierre del día anterior, en los casos donde se presentaron dos o más días consecutivos sin información, se suplieron calculando un promedio móvil de 5 días.
Como se mencionó anteriormente, se recolectaron los datos de precio de cierre de las 24 acciones contenidas en la canasta 32 del índice COLCAP desde enero 5 de 2009 hasta noviembre 11 de 2015, sin embargo, algunas de estas acciones empezaron a cotizar en la BVC varios años después del 2009. Es necesario tener el mayor número posible de datos comprendidos dentro del mismo periodo de tiempo para todas las acciones, por lo tanto, se excluyeron de los cálculos las acciones PFCEMARGOS, PFAVAL, CLH, PFAVH, PFGRUPOARG y PFGRUPOSURA, pues no empezaron a cotizar en la BVC hasta después del 2011. Finalmente quedaron 18 acciones dentro del periodo comprendido entre el 6 de octubre de 2010 hasta el 11 de noviembre de 2015, para un total de 1246 días bursátiles.
Gráfico 1
Proceso para la estimación de un portafolio utilizando el criterio de Kelly

Fuente: Elaboración propia
Una vez recolectados los datos y definido el periodo de tiempo dentro del que se iba a trabajar, se procedió con la estimación los cálculos necesarios para la aplicación del criterio de Kelly, los cuales se pueden observar en la Tabla 1, junto a otra serie de datos útiles para analizar el desempeño de cada una de las 18 acciones seleccionadas.
Gráfico 2
Composición de la canasta 32 del índice COLCAP de la bolsa de valores de Colombia.
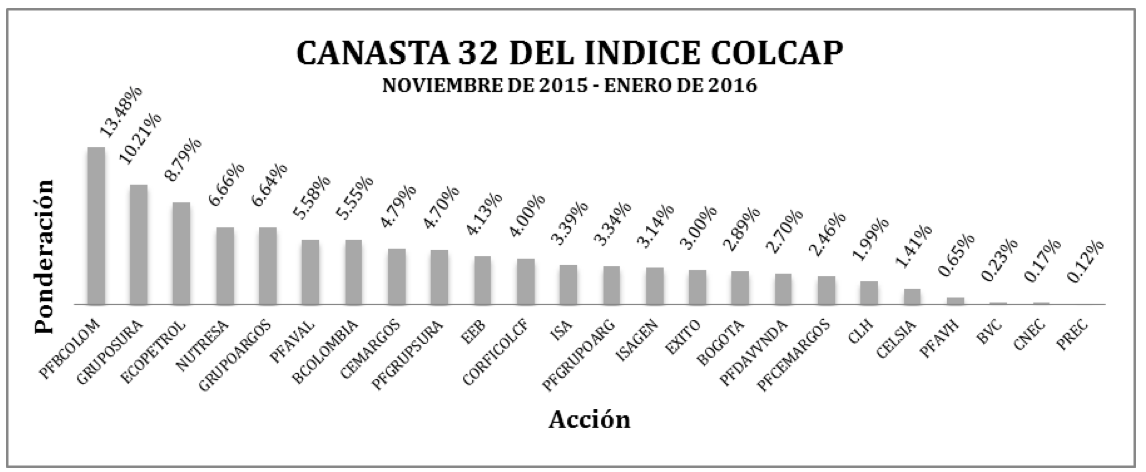
Fuente: Elaboración Propia.
-----
Tabla 1
Datos del desempeño de una acción.

Fuente: Elaboración propia



Gráfico 3
Riesgo Vs Rentabilidad
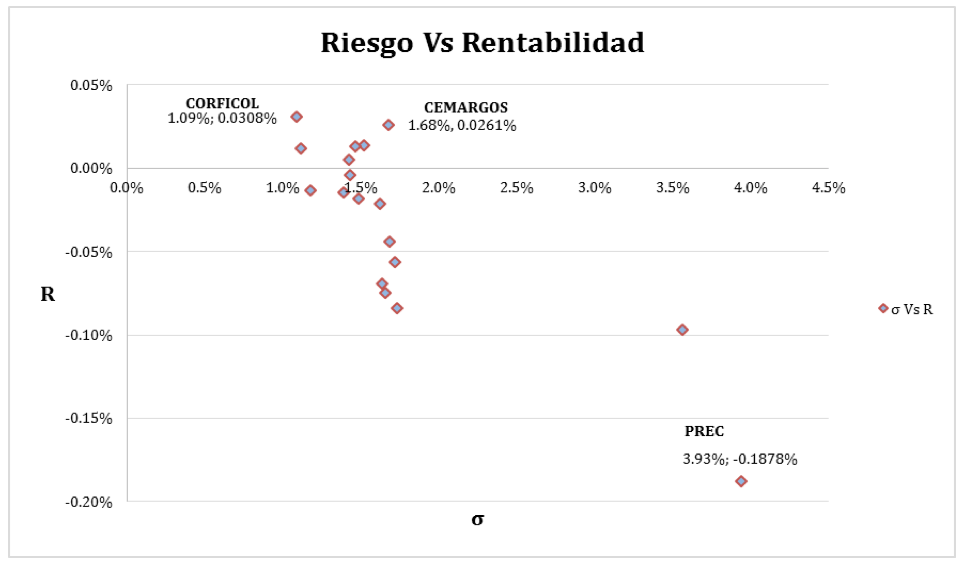
Fuente: Elaboración propia.

Gráfico 4
Probabilidad de ganancia, Vi vs Ai

Fuente: Elaboración propia.



Gráfico 5
Relación entre los días ganadores y perdedores, y sus rentabilidades promedio

Fuente: Elaboración propia.

Gráfico 6
Resultado del portafolio utilizando el criterio de Kelly
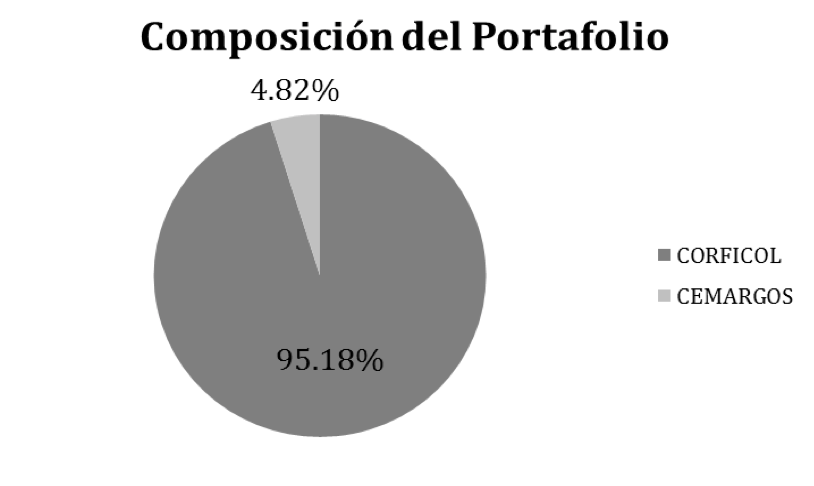
Fuente: Elaboración propia.

Un inversionista siempre buscará opciones donde las probabilidades de ganar sean mayores a las de perder. Frente a las opciones favorables, el inversionista podría invertir todo su capital para maximizar su ganancia esperada, pero quedaría en la ruina, por lo tanto, esta estrategia es inútil. Otro enfoque podría ser minimizar la probabilidad de quedar en la ruina, pero esto le dejaría muy pocas ganancias, lo que convierte a las inversiones pequeñas en una opción poco atractiva.Una estrategia apropiada sería distribuir el capital de inversión en diferentes activos de forma tal que, se pueda esperar el mayor retorno esperado posible. Esto se puede lograr con la ayuda del criterio de Kelly, como se ha discutido en este trabajo.
El criterio de Kelly ha sido utilizado con éxito por varios inversionistas en los últimos años. Poundstone popularizó este hecho en su libro: “Fortune’s formula : the untold story of the scientific betting system that beat the casinos and Wall Street. Hill and Wang” (Poundstone, 2005), donde se dice que inversionistas como Warren Buffet y Bill Gross distribuyen su capital en formas que son consistentes al criterio de Kelly, incluso Edward Thorp, uno de los referentes más importantes en el desarrollo del tema, aplica abiertamente el criterio de Kelly como su regla principal de distribución de portafolio (Zambrano, 2014), y dirigió dos fondos de cobertura que reportaron ganancias positivas por 30 años seguidos, con promedios de entre el 19% y 20% de retorno anuales (Patterson, 2008).
Se demostró una forma de construir un portafolio que permite maximizar la rentabilidad esperada con las acciones que conforman la canasta 32 del índice COLCAP de la BVC, usando el criterio de Kelly. Esta herramienta de análisis estima la probabilidad de perdida y ganancia, las rentabilidades promedio esperadas asociadas a esas probabilidades, y les da mayor importancia a las acciones en las que la interacción entre estas características arroja los mejores resultados.
Para este caso, se obtiene un portafolio muy poco diversificado y con pocas acciones, hecho que concuerda con los resultados obtenidos por Laureti, Medo y Zhang (Laureti et al., 2009). Para el periodo analizado, el criterio de Kelly sugiere invertir en un portafolio conformado por CORFICOL en un 95.18%, y por CEMARGOS en un 4.82%.
Este resultado refleja el coeficiente de variación, en el que CORFICOL se destaca por tener la mayor rentabilidad y el menor riesgo dentro del conjunto de acciones estudiadas, también refleja los resultados plasmados en la parte derecha del Gráfico 4, donde se observa que la interacción entre los días ganadores y perdedores, y sus rentabilidades asociadas, arrojan los indicadores más positivos para CORFICOL y CEMARGOS; 1.09 y 1.04 respectivamente.
El portafolio estimado a través de este método arroja una rentabilidad esperada del 0.28%, la cual es más alta que la esperada con la estrategia pasiva de invertir en el índice COLCAP, que resulta en una rentabilidad esperada de -0.023%.
Este trabajo brinda bases para futuras investigaciones, en las que se considere el cálculo de portafolios a través de la metodología tradicional de media-varianza, y el posterior contraste con los resultados obtenidos mediante el criterio de Kelly. Otra alternativa de investigación se fundamenta en proponer una herramienta que complemente esta metodología para determinar el tiempo necesario para obtener excedentes de rentabilidad. Así mismo, entre los trabajos de investigación futuros que pueden tomar como base esta investigación se encuentran aquellos que consideren factores como costos de transacción, impuestos y restricciones de liquidez del activo, los cuales no siempre son pequeños ni pueden ser ignorados (Lv & Meister, 2010).
Fama, E. F. (1965). The Behavior of Stock-Market Prices. The Journal of Business, 38, 34–105. http://doi.org/10.2307/2350752
Hung, J. (2010). Betting with the Kelly Criterion. Retrieved from https://www.math.washington.edu/~morrow/336_10/papers/jane.pdf
Kelly, J. L. (1956). A New interpretation of Information rate. Bell System Technical Journal, 35, 917–926. Retrieved from https://www.princeton.edu/~wbialek/rome/refs/kelly_56.pdf
Kim, G., & Jung, S. (2014). A Portfolio Comparison of a Kelly Criterion with Markowitz Model : A Case Study with KOSPI 200. In Proceedings of the 2014 International Conference on Industrial Engineering and Operations Management Bali, Indonesia, January 7 – 9, 2014. Bali. Retrieved from http://ieomsociety.org/ieom2014/pdfs/192.pdf
Kim, G., & Suhee, J. (2013). The Construction of the Optimal Investment Portfolio Using the Kelly Criterion. World Journal of Social Sciences, 3, 15–26. Retrieved from file:///C:/Users/Sebas/AppData/Local/Mendeley Ltd./Mendeley Desktop/Downloaded/Kim, Suhee - 2013 - The Construction of the Optimal Investment Portfolio Using the Kelly Criterion.pdf
Laureti, P., Medo, M., & Zhang, Y.-C. (2009). Analysis of Kelly-optimal portfolios. Quantitative Finance, 10(7), 689–697. http://doi.org/10.1080/14697680902991619
Lundström, C. (2014). Money ;anagement with Optimal Stopping of Losses for Maximizing the Returns of Futures Trading. Umeá University, Department of Economics. Retrieved from http://ideas.repec.org/p/hhs/umnees/0884.html
Lv, Y., & Meister, B. K. (2010). Implication of the Kelly Criterion for Multi-Dimensional Processes. International Journal of Theoretical & Applied Finance, 13(1), 93–112. http://doi.org/10.1142/S0219024910005693
MacLean, L. C., Zhao, Y., & Ziemba, W. T. (2016). Optimal Capital Growth with Convex Shortfall Penalties. Quantitative Finance, 16(1), 101–117. http://doi.org/10.1080/14697688.2015.1059469
Markowitz, H. (1959). Portfolio Selection. The Journal of Finance, 7(1), 77–91. http://doi.org/10.1111/j.1540-6261.1952.tb01525.x
Osorio, R. (2009). A prospect-theory approach to the Kelly criterion for fat-tail portfolios: the case of Student’s t-distribution. Wilmott Journal, 1(2), 101–107. http://doi.org/10.1002/wilj.7
Patterson, S. (2008). Old Pros Size Up the Game. Wall Street Journal, pp. A9–A9. Retrieved from https://www.wsj.com/articles/SB120614130030156085
Phatarfod, R. (2012). Kelly Gambling with the Stock Market and Banks. Mathematical Scientist, 37(2), 132–140. Retrieved from http://www.scopus.com/inward/record.url?eid=2-s2.0-84871896737&partnerID=40&md5=81627003d6a678fff100a1b438fdf52c
Piotrowski, E. W., & Schroeder, M. (2007). Kelly criterion revisited: Optimal bets. European Physical Journal B, 57(2), 201–203. http://doi.org/10.1140/epjb/e2007-00126-3
Poundstone, W. (2005). Fortune’s formula : the untold story of the scientific betting system that beat the casinos and Wall Street. Hill and Wang. Retrieved from https://www.mendeley.com/research-papers/fortunes-formula-untold-story-scientific-betting-system-beat-casinos-wall-street/?utm_source=desktop&utm_medium=1.17.9&utm_campaign=open_catalog&userDocumentId=%7B283cc610-15ab-412b-90d7-b34ff58e569f%7D
Rotando, L. M., & Thorp, E. O. (1992). The Kelly Criterion and the Stock Market. The American Mathematical Monthly, 99(10), 922–931. http://doi.org/10.2307/2324484
Scholz, P. (2012). Size matters! How Position Sizing Determines Risk and Return of Technical Timing Strategies. Frankfurt School of Finance & Management, Centre for Practical Quantitative Finance (CPQF). Frankfurt School of Finance and Management, Centre for Practical Quantitative Finance (CPQF). Retrieved from http://ideas.repec.org/p/zbw/cpqfwp/31.html
Sewell, M. (2011). Money Management. Retrieved from file:///C:/Users/Sebas/AppData/Local/Mendeley Ltd./Mendeley Desktop/Downloaded/Sewell - 2011 - Money Management.pdf
Subbiah, M., & Fabozzi, F. J. (2016). Hedge Fund Allocation: Evaluating Parametric and Nonparametric Forecasts Using Alternative Portfolio Construction Techniques. International Review of Financial Analysis, 45, 189–201. http://doi.org/10.1016/j.irfa.2016.03.003
Thorp, E. O. (1969). Optimal Gambling Systems for Favorable Games. Revue de l’Institut International de Statistique / Review of the International Statistical Institute, 37(3), 273–293. http://doi.org/10.2307/1402118
Thorp, E. O. (1975). Portfolio Choice and the Kelly Criterion. In Stochastic Optimization Models in Finance (pp. 599–619). http://doi.org/10.1016/B978-0-12-780850-5.50051-4
Thorp, E. O. (1980). The Kelly Money Management System. Gambling Times, 91–92. Retrieved from file:///C:/Users/Sebas/AppData/Local/Mendeley Ltd./Mendeley Desktop/Downloaded/Thorp - 1980 - The Kelly Money Management System.pdf
Thorp, E. O. (2008). The Kelly Criterion in Blackjack Sports Betting, and the Stock Market. In S. A. Z. T. Ziemba (Ed.), Handbook of Asset and Liability Management (Vol. 1, pp. 385–428). San Diego: North-Holland. http://doi.org/http://dx.doi.org/10.1016/B978-044453248-0.50015-0
Thorp, E. O., MacLean, L. C., & Ziemba, W. T. (2010). Understanding the Kelly Criterion. In E. O. T. Leonard C. MacLean William T. Ziemba (Ed.), The Kelly Capital Growth Investment Criterion: Theory and Practice (pp. 509–523). Singapore: World Scientific Press. http://doi.org/10.1016/j.jcis.2005.12.025
Zambrano, E. (2014). Subtle Price Discrimination and Surplus Extraction Under Uncertainty. Journal of Mathematical Economics, 52(0), 153–161. http://doi.org/http://dx.doi.org/10.1016/j.jmateco.2013.08.004
1. Economista, Universidad de Antioquia, Medellín, Colombia. Candidata a Doctor en ingeniería industria y organizaciones, Universidad Nacional de Colombia. Magister en Administración financiera y Magister en Finanzas, universidad EAFIT, Medellín, Colombia. Docente de Universidad de Medellín, Medellín, Colombia. Docente Universidad Nacional de Colombia. Correo electrónico: moarango@udem.edu.co
2. Candidato a Magister en Finanzas, Universidad de Medellín, Colombia, Ingeniero de sonido, Universidad de San Buenaventura, Medellín, Colombia. Correo electrónico: sebasalzatel@gmail.com
3. Magíster en Ciencias Estadísticas de la Universidad Nacional de Colombia. Docente de la Universidad de Medellín. Correo electrónico: dsguzman@udem.edu.co