

Vol. 39 (Nº 04) Ano 2018 Pág. 25
Deivison da Silveira PEREIRA 1; Luana Carneiro BRANDÃO 2; Renata Raposo DEL-VECCHIO 3; João Carlos C. B. SOARES DE MELLO 4
Recebido: 24/09/2017 • Aprovado: 30/10/2017
3. Estudo de caso e resultados
RESUMO: O presente estudo faz integração as centralidades em grafos, através do método multicritério de Copeland, para avaliar a malha aérea para uma companhia de aviação comercial brasileira, utilizando os dados de voos homologados. O modelo permite a identificação dos hubs para essa companhia, considerando a capacidade dos aeroportos de intermediar o fluxo de voos entre os demais (fluxo de intermediação), a sua conexão com outros aeroportos bem conectados (autovetor) e a sua proximidade, em termos de tempo de voo (proximidade). (menos de 80 palavras) |
ABSTRACT: This study uses Copeland’s multiple criteria method to combine graph centrality measures and evaluate the air network for a commercial Brazilian aviation company, using the approved flights data. The method proposed herein identifies the company’s hubs, while taking into account the airports’ capacity to intermediate flights between other airports (flow betweenness centrality), the airports’ connections with connected airports (eigenvector centrality), and how close they are to other airports, in terms of flight duration (closeness centrality). |
Os estudos na área de tráfego aéreo são especialmente importantes, por sua relação com o desenvolvimento econômico do país (Green, 2007; Brueckner, 2013). De fato, os aeroportos são tidos como ativos estratégicos pelos governos, e também levados em consideração pelas empresas em suas decisões estratégicas (Bel et al, 2008).
Diversos estudos nessa área buscam localizar os pontos centrais para a otimização das rotas aéreas (Jaillet et al, 1997). A partir da localização desses pontos centrais, é possível adotar uma malha aérea do tipo hub and spoke, em que os diversos aeroportos de menor porte se conectam aos hubs mais próximos, enquanto os hubs são conectados entre si, permitindo ganhos de escala e a maximização de lucros (Hansen, 1990).
Paralelamente, a definição dos pontos centrais de uma rede envolve a identificação dos seus pontos mais impactantes, os quais podem ser calculados com base em medidas de centralidade (Ercsey-Ravasz et al, 2012). De fato, Bergiante et al (2011) aplicaram uma medida de centralidade em uma malha pequena de uma empresa brasileira, que atualmente não opera mais.
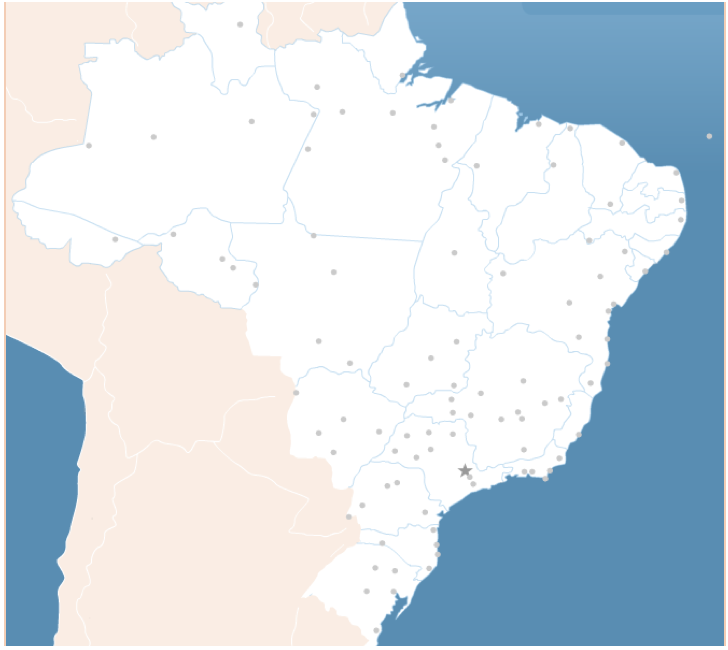
Inserido nessa linha de estudo, o presente trabalho utiliza medidas de centralidade para avaliar a malha de rotas domésticas da empresa Azul Linhas Aéreas para identificar os pontos mais impactantes desta rede no território brasileiro. A Figura 1 apresenta os aeroportos de atuação da companhia.
Figura 1
Mapa de atuação da Azul
Medidas de centralidade avaliam a importância de um elemento com relação a uma rede e são fundamentadas em teoria dos grafos (Freeman, 1979). Como a nomenclatura e representações matemáticas utilizadas em estudos dessa área variam significativamente, apresenta-se a seguir a aquelas utilizadas no presente trabalho, em linha com Bondy e Murty (2008).

De maneira geral, a centralidade avalia a importância relativa de um vértice em uma rede (Bergiante et al., 2011), e pode ser medida de diversas formas distintas, com significados e interpretações distintos.
A centralidade de intermediação tem como objetivo medir a frequência com que um vértice se situa entre dois outros setores do grafo, tomando como referência o caminho geodésico (menor caminho) entre eles:



2.3. Método multicritério Copeland
De acordo com Arrow (1951), métodos ordinais justos obedeceriam aos seus axiomas, quais sejam, independência de alternativas irrelevantes, transitividade e universalidade. O primeiro exige que a ordem de preferência entre duas alternativas não deve depender de uma terceira. O segundo axioma exige que não exista ciclos de intransitividade, i.e., se uma alternativa é preferível a uma segunda, e se essa segunda é preferível a uma terceira, então a primeira alternativa deve ser preferível à terceira. O terceiro axioma exista que os demais sejam respeitados em quaisquer casos, e não em situações específicas.
Arrow (1951) também demonstra que não existem métodos ordinais não-ditatoriais justos. Entretanto, segundo Soares de Mello et al (2015), os métodos ordinais mais utilizados na literatura são Borda, Condorcet e Copeland. No método de Borda (Barba-Romero e Pomerol, 1997), cada alternativa recebe um número pré-definido de pontos, conforme a sua ordenação em cada critério. Em seguida, as alternativas são ordenadas de acordo com o somatório de pontos em todos os critérios. Embora seja simples, esse método é dependente de alternativas irrelevantes (Soares de Mello et al, 2005).
Já o método de Condorcet (Barba-Romero e Pomerol, 1997) identifica, para cada par de alternativas, aquela que é preferida pela maioria dos critérios, podendo haver empates, caso em que as alternativas do par em questão serão tidas como indiferentes entre si. A ordenação final provém dessa análise por pares, podendo apresentar ciclos de intransitividade.
Já o método de Copeland (1951) é derivado do método de Condorcet, iniciando-se com a mesma comparação por pares, em que uma alternativa pode vencer ou empatar com outra. Em seguida, o método soma as vitórias (e empates) e subtrai as derrotas de cada alternativa, ordenando as alternativas de acordo com esse resultado (Barba-Romero e Pomerol, 1997). Quando não há ciclos de intransitividade, os métodos de Condorcet e Copeland fornecem a mesma ordenação e são considerados justos pelos axiomas de Arrow, sendo, portanto, preferíveis ao método de Borda nessa situação (Soares de Mello et al, 2005). Quando tais ciclos existem, Copeland ordena as alternativas, tornando-se transitivo, porém dependente de alternativas irrelevantes dentro desses ciclos. Dessa forma, utiliza-se o método ordinal de Copeland no presente trabalho, por ser uma proposta intermediária entre os demais.
Soares de Mello et al. (2005), por exemplo, utilizam o método de Copeland para classificar os pilotos de Fórmula 1 no campeonato de 2002. A classificação oficial apresenta-se um pouco distinta desta porque, oficialmente, apenas os seis primeiros pilotos pontuam, porém no método de Copeland, todos os resultados são levados em conta.
Os dados utilizados neste estudo são baseados na tabela HOTRAN (Horário de Transporte), onde são registrados, pelo órgão governamental regulador do setor de aviação civil, a ANAC, os voos comerciais regulares (domésticos e internacionais) de transporte de passageiros e também de carga, do dia 23 de junho de 2015. A nomenclatura de códigos de cada aeroporto utilizada neste estudo será conforme esta tabela que segue o ICAO (Internacional Civil Aviation Organization). Foram utilizados os voos da Azul Linhas Aéreas que partem às segundas feiras, dia da semana definido por ser o dia com a maior quantidade de destinos disponíveis.
Com base nesses dados, calculam-se as medidas de centralidade de intermediação de fluxo, de autovetor e de proximidade. Segue-se, então, a análise multicritério, em que cada tipo de centralidade torna-se um critério. Em função das características de cada medida de centralidade, a alternativa é melhor avaliada quanto maior for o valor da sua centralidade de autovetor e de intermediação, e quanto menor for o valor da sua centralidade de proximidade.
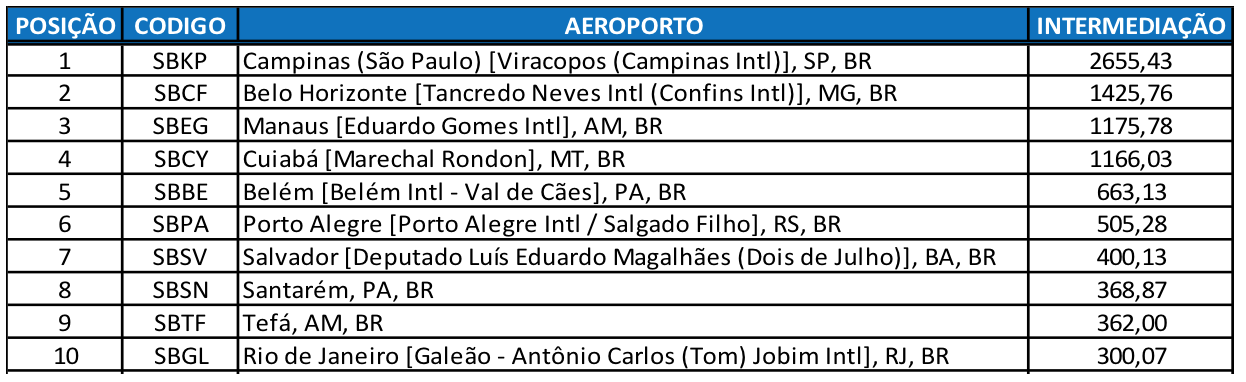
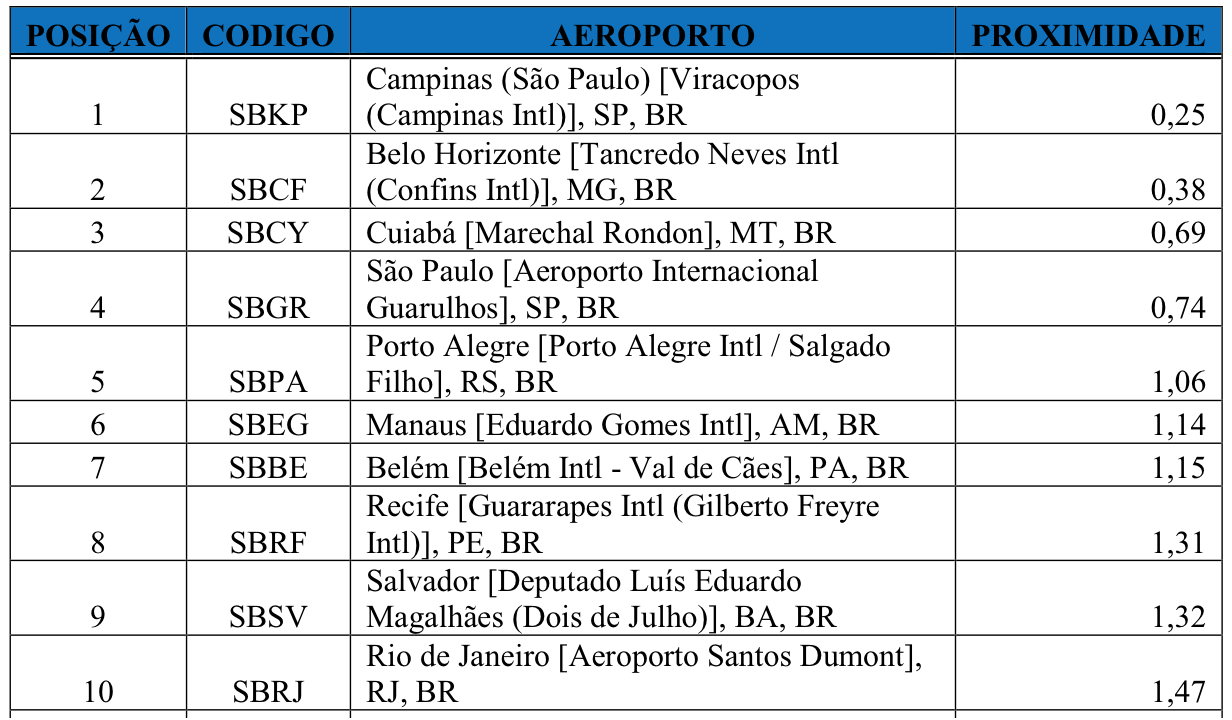
Para o cálculo da centralidade de fluxo de intermediação, foi utilizado o software Unicet 6.0 (Borgatti et al, 2002). A Tabela 1 apresenta esse resultado para os 10 aeroportos mais centrais, em termos de fluxo de intermediação, da malha da Azul. A Figura 2 apresenta o grafo dos aeroportos da Tabela 1, com base nas suas medidas de fluxo de intermediação, obtido pelo software Netdrawn (Borgatti, 2002).
Tabela 1
Ranking dos 10 primeiros aeroportos para intermediação
-----
Figura 2
Grafo da malha aérea – fluxo de intermediação
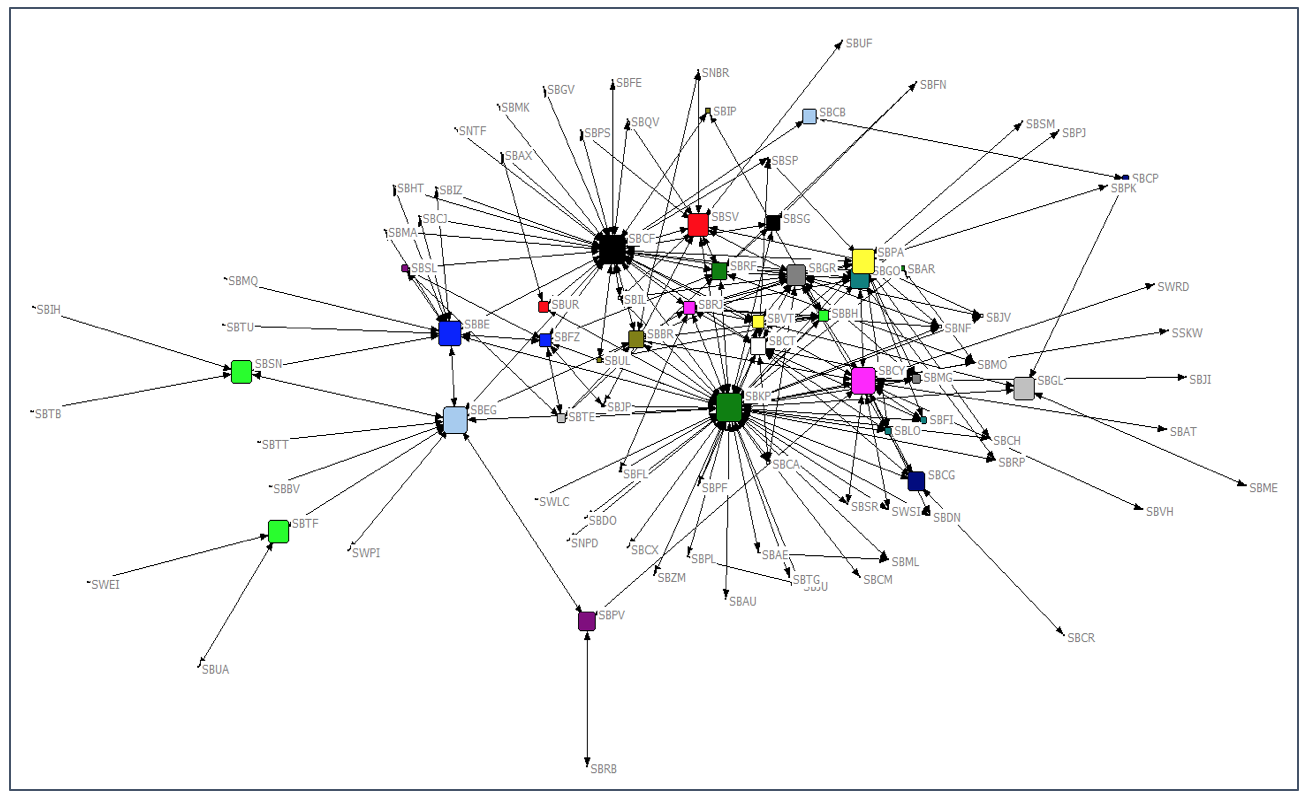
Analisando a Tabela 1 e a Figura 2, destacam-se o aeroporto de Campinas como o principal da malha da Azul, seguido por Belo Horizonte e por Manaus como os mais importantes para o fluxo de intermediação.
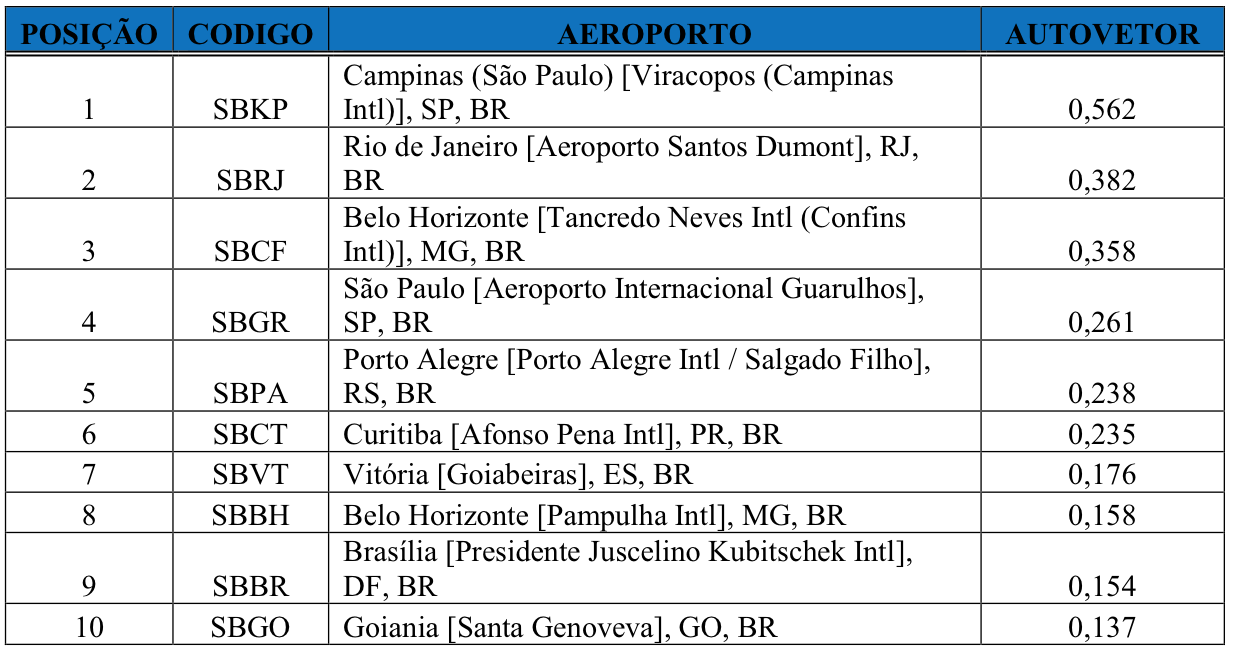
Para o cálculo da centralidade de autovetor, também foi utilizado o software Unicet 6.0 (Borgatti et al, 2002), sendo os 20 aeroportos mais centrais, em termos de autovetor, apresentados na Tabela 2. A Figura 3 apresenta o grafo dos aeroportos da Tabela 2, com base nas suas medidas de autovetor, obtido pelo software Netdrawn (Borgatti, 2002).
Tabela 2
Ranking dos 10 primeiros aeroportos para autovetor
-----
Figura 3
Grafo da malha aérea – centralidade de autovetor
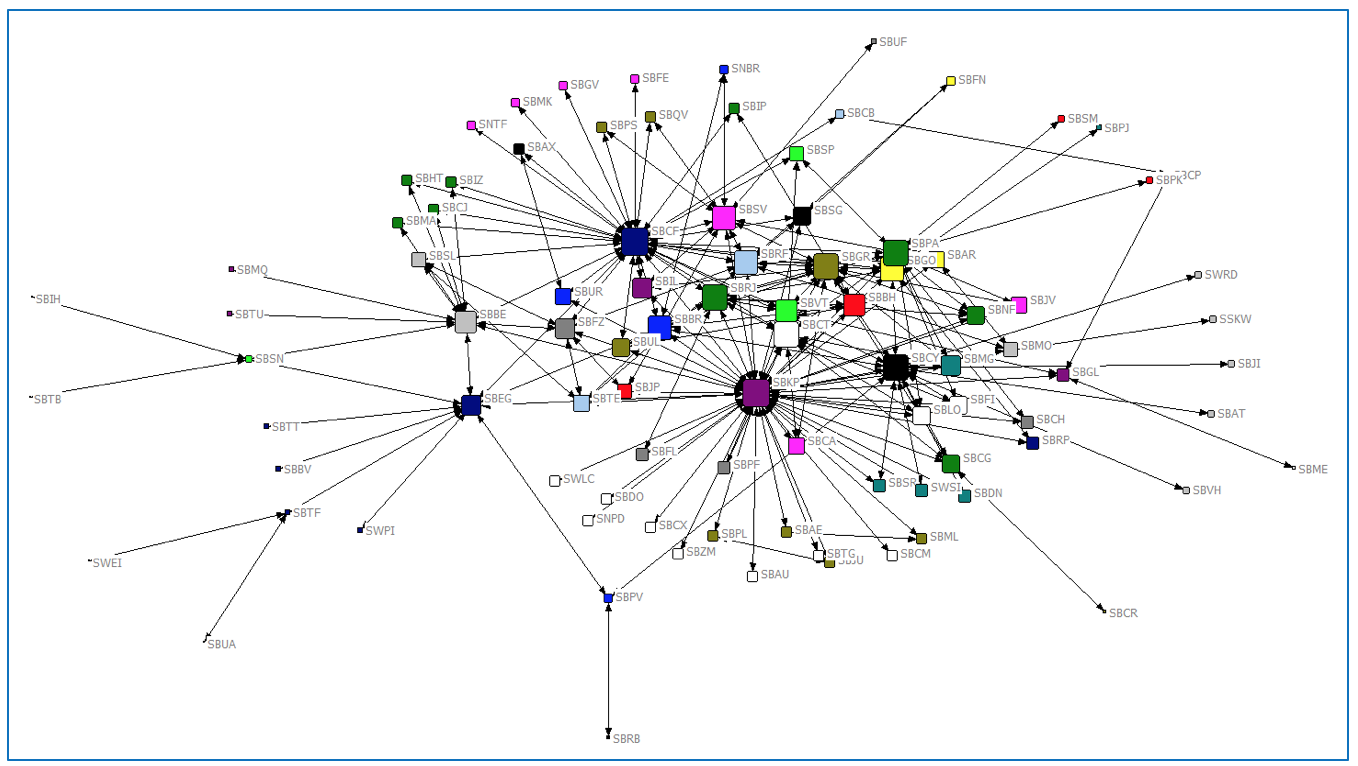
Mais uma vez verifica-se pela Tabela 2 e a Figura 3 o aeroporto de Campinas como o mais importante, sendo que também pela medida de autovetor. No entanto, neste caso foi seguido pelo aeroporto Santos Dumont, localizado no Rio de Janeiro.
Para o cálculo da centralidade de proximidade, considerou-se a média dos tempos de voos verificados na tabela da HOTRAN. A Tabela 3 apresenta a ordenação dos 20 aeroportos mais centrais, em termos de proximidade, da malha da Azul. A Figura 4 apresenta o grafo associado
Tabela 3
Ranking dos 10 primeiros aeroportos para proximidade
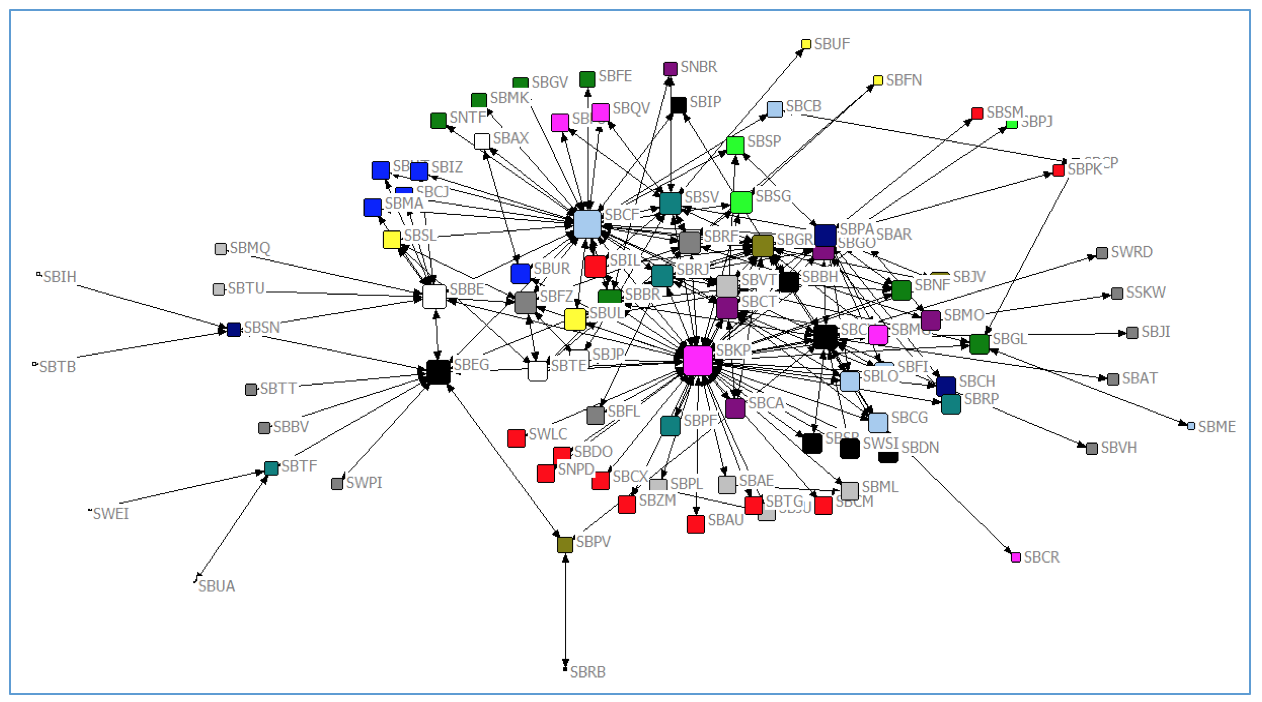
Ressalta-se a importância do aeroporto de Campinas para malha em proximidade também, no entanto os aeroportos seguintes estão mais distribuídos pelo território nacional de acordo com esta medida.
Figura 4
Grafo da malha aérea – centralidade de proximidade
A integração das centralidades pelo método de Copeland considera os aeroportos como alternativas no modelo, e os tipos de centralidade como os critérios de avaliação. A Tabela 4 apresenta a ordenação de Copeland, obtida com o emprego do software WebPROA (Bittencourt & Angulo-Meza, 2013), dos 30 aeroportos da malha da Azul mais centrais, considerando as 3 centralidades em conjunto avaliada pelo Copeland.
Tabela 4
Ranking dos 30 primeiros aeroportos ordenados pelo Copeland

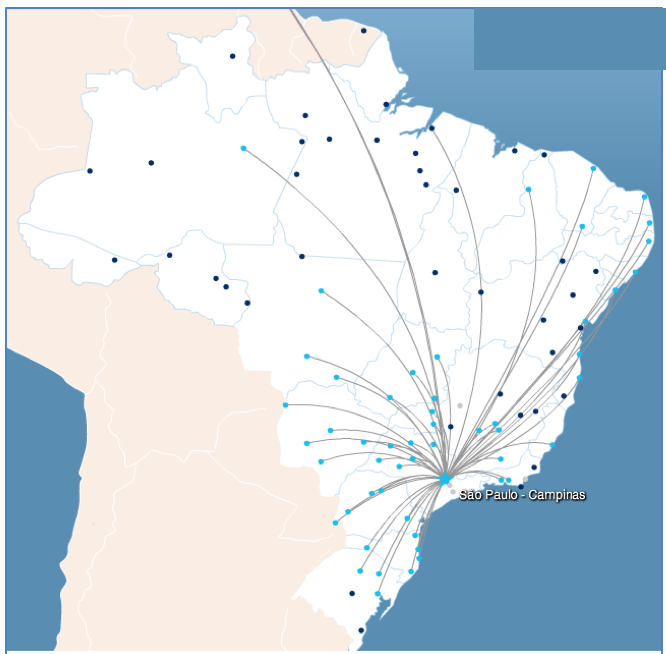
Verifica-se que o aeroporto de Viracopos (Campinas/SP) é o principal aeroporto da malha da empresa Azul Linhas Aéreas, segundo as três medidas de centralidade. Foi neste aeroporto que a empresa iniciou suas operações e mantém a maior parte dos seus voos, conforme a Figura 5.
Figura 5
Rotas a partir de Campinas/SP
Para as medidas de intermediação e proximidade, o segundo principal é o aeroporto de Confins (Belo Horizonte/MG), sendo que para autovetor o segundo mais importante é o aeroporto Santos Dumont (Rio de Janeiro/RJ). Nesta medida de centralidade, os aeroportos do Sul e Sudeste se destacam como importantes para propagação de qualquer impacto nessa região para o restante do país. Para proximidade os aeroportos de Campinas, Belo Horizonte (Confins), Cuiabá e São Paulo se destacam, apresentando uma concentração maior nas regiões centrais do país. A Figura 6 apresenta as rotas com origem o aeroporto de Confins em Belo Horizonte/MG.
Figura 6
Rotas a partir de Belo Horizonte/MG

Com a análise integrada do Copeland, Campinas continua como principal aeroporto e os demais apresentam uma ordenação similar à medida de proximidade nas primeiras posições, com o destaque para Guarulhos e Cuiabá que se tornaram forte dentro da malha principalmente após a fusão com TRIP, visto que era uma empresa mais focada na aviação regional, como pode ser visto nas Figuras 7 e 8.
Figura 7
Rotas a partir de Guarulhos/SP

-----
Figura 8
Rotas a partir de Cuiabá/MT

Com a integração das centralidades através do método de Copeland, verifica-se dentro da malha da Azul uma distribuição da importância dos aeroportos em todas as regiões do país, considerando os 10 primeiros na ordenação. A capilaridade da rede leva a importância para outras regiões, mas os 5 principais continuam no centro-sul brasileiro.
Este estudo utilizou o método multicritério ordinal de Copeland para combinar três tipos de centralidade, todas elas relevantes para a localização de aeroportos, obtendo-se uma única ordenação, a qual identifica os pontos centrais da operação, considerando as múltiplos medidas de centralidade.
Essa análise apresenta-se como importante ferramenta para uma empresa do setor aéreo, permitindo verificar os hubs da sua operação. Com a identificação desses pontos, a empresa é capaz de planejar os locais para atender a demanda, e avaliar os possíveis riscos para a rede, no caso de falha em qualquer desses pontos na malha.
Neste estudo não foi considerado o tipo de aeronave, ou o tamanho do aeroporto em número de passageiros, com uma análise futura poderá considerar esses fatores como critérios adicionais. Além disto, uma verificação dos investimentos realizados poderá ser revista em outros modelos para avaliação da eficiência de cada localidade.
Estudos futuros devem ser feitos para verificar possíveis medidas de centralidade com outras metodologias e as implicações na operação da companhia aérea, bem como analisar o comportamento da malha brasileira agregando dados de todas as companhias que operam no país.
Arrow, K.J. (1951) Social Choice and Individual Values. New York: Wiley.
Azul (2015). Conheça a História da Azul. Disponível em http://www.voeazul.com.br/sobre-azul, acessado em 23/06/15.
Anac (2015). HOTRAN- Horário de Transporte. Disponível em http://www2.anac.gov.br/hotran/, acessado em 23/06/15.
Barba-Romero, S. &Pomerol, J.C. (1997). DecisionesMulticriterio: Fundamentos Teóricos y Utilización Práctica, Colección de Economía. Universidad de Alcalá, Espanha.
Bel, G., Fageda, X. (2008). Getting there fast: globalization, intercontinental flights and location of headquarters. Journal of Economic Geography, 8, 471-495
Bergiante, N.C.R., Soares de Mello, J.C.C.B., Nunes, M.V.R., Paschoalino F.F. (2011) Aplicação de uma proposta de medida de centralidade para avaliação de malha aérea de uma empresa do setor de transporte aéreo brasileiro, Journal of Transport Literature, 5(4), 119-135.
Bittencourt, M., Angulo-Meza, L. (2013). WEB PROA Software Livre para os Métodos Multicritérios à Decisão Borda Condorcet e Copeland. In: XLV Simpósio Brasileiro de Pesquisa Operacional, 2013, Natal. Anais do XLV Simpósio Brasileiro de Pesquisa Operacional, 2013.
Bonacich, P., (1987), “Power and Centrality: A Family of Measures”, The American Journal of Sociology, v. 92, n 5, pp. 1170-1182.
Bondy, A.; Murty, U.S.R. (2008). Graph Theory. Springer, 2008, XII, 651 p.
Borgatti, S.P. 2002. NetDraw: Graph Visualization Software. Harvard: Analytic Technologies
Borgatti, S.P.; Everett, M.G. and Freeman, L.C. Ucinet for Windows: Software for Social Network Analysis. Harvard, MA: Analytic Technologies, 2002.
Bruechner, J. K. (2013), Airline traffic and urban economic development. Urban Studies, 40, 1455-1470
Del-Vecchio, R.R., Galvão, D.J.C., Silva, L., de Lima, R.F.V.L. (2009) Medidas de Centralidade da Teoria dos Grafos aplicada a Fundos de Ações no Brasil. Em: XLI Simpósio Brasileiro de Pesquisa Operacional, Porto Seguro, Brasil, 1-4 de Setembro de 2009.
Freeman, L. C., (1977), “A Set of Measures of Centrality Based on Betweenness”, Sociometry, v. 40, n. 1, pp. 35-41.
Freeman, L.C. (1979) Centrality in networks: I Conceptual clarification. Social Networks, 1, 215-239.
Freeman L C, Borgatti S P and White D R (1991).Centrality in valued graphs: A measure of betweenness based on network flow. Social Networks 13, 141-154.
Ercsey-Ravasz, M.; Lichtenwalter, R.; Chawla, N. V.; Toroczkai, Z. (2012). Range-limited Centrality Measures in Complex Networks. Physical Review E, 85(6), 66-103.
Everton, S.F. (2012) Disrupting Dark Networks (Structural Analysis in the Social Sciences). Cambridge University Press, New York, NY, USA.
Grassi, R. Stefani, S., Torriero, A. (2007), Some New Results on the Eigenvector Centrality, Journal of Mathematical Sociology, 31:237–248
Green, R. (2007), Airports and economic development. Real estate economics, 35, 91-112
Hansen, M. (1990), Airline competition in a hub-dominated environment: an application of noncooperative game theory. Transportation Research Part B, 24, 27-43
Jaillet, P., Song, G., Yu, G. (1996), Airline network design and hub location problems. Location Science, 4, 195-212
Sabidussi, G., 1966, “The centrality index of a graph”, Psychometrika, v. 31, pp. 581-603.
Soares de Mello, J.C.C.B., Gomes, L.F.A.M., Gomes, E.G., Soares de Mello, M.H.C. (2005). Use of ordinal multi-criteria methods in the analysis of the Formula 1 World Championship. Cadernos EBAPE.BR, III(2), 1-8.
Soares de Mello, J.C.C.B., Gomes Junior, S.F., Angulo-Meza, L. and Mourão, C.L.O. (2015) Condorcet Method with Weakly Rational Decision Makers: A Case Study in the Formula 1 Constructors’ Championship. Procedia Computer Science 55(2015) 493-502. DOI: 10.1016/j.procs.2015.07.024
1. Doutorando em Engenharia de Produção. Universidade Federal Fluminense - UFF. Escola de Engenharia. Departamento Pós Graduação em Engenharia de Produção. dspereira@id.uff.br
2. Doutorando em Engenharia de Produção. Universidade Federal Fluminense – UFF. Escola de Engenharia. Departamento Pós Graduação em Engenharia de Produção.
3. Doutora de Matemática. Universidade Federal Fluminense - UFF. Instituto de Matemática. Departamento de Análises. renata@vm.uff.br
4. Doutor em Engenharia de Produção. Universidade Federal Fluminense -UFF . Escola de Engenharia. Departamento Pós Graduação em Engenharia de Produção. jcsmello@producao.uff.br