ISSN 0798 1015

Vol. 39 (Nº 03) Año 2018. Pág. 10

Modelo de teoría de restricciones con consideraciones de optimización y simulación – Un caso de estudio

Theory of constraints model with optimization and simulation considerations - A case study

Germán HERRERA-VIDAL 1; Jorge CAMPO-JUVINAO 2; Jhony BERNAL-HERNANDEZ 3; Richard TILVES-MARTINEZ 4

Recibido: 06/09/2017 • Aprobado: 30/09/2017

Contenido

1. Introducción

2. Materiales y métodos

3. Resultados

4. Conclusiones

Referencias bibliográficas

1. Introducción

En un mundo globalizado como el actual, la velocidad y precisión en la toma de decisiones, juega un papel importante a la hora de mejorar los procesos productivos en un entorno empresarial. Debido a que una respuesta rápida involucra tener que atender las necesidades de un mercado en el menor costo y tiempo posible. Es por esto que todas las empresas hoy en día buscan familiarizarse con un proceso de mejoramiento continuo que se ajuste a las tendencias actuales de tal manera que logren incrementar su productividad y por su puesto su competitividad.

Según Goldratt (1993), la teoría de restricciones (TOC) es todo un proceso de mejoramiento continuo, basado en un pensamiento sistémico, que ayuda a las empresas a incrementar sus utilidades con un enfoque simple y práctico, identificando las restricciones para lograr sus objetivos, y permitiendo efectuar los cambios necesarios para eliminarlos. A su vez Morales (2006) establece que las empresas que utilizan la teoría de restricciones como herramienta para el mejoramiento continuo de sus procesos logran fortalecer su competitividad a nivel de calidad, servicio al cliente y bajo costo; logran también la reducción en el tiempo de entrega, mejora en el cumplimiento de las fechas de entrega, reducción en los inventarios, incremento de las ventas y el incremento de las utilidades netas.

De acuerdo con Goldratt (1998), el concepto restricción, es entendido como el factor que impide a las empresas alcanzar su meta, entendiendo como meta la razón para que el sistema exista. Para empresas con ánimo de lucro, la meta será ganar más dinero ahora y en el futuro; para empresas sin ánimo de lucro, la meta será generar más unidades de meta, es decir, generar más salud en el caso de los hospitales, más educación en el caso de los centros educativos, o más seguridad en el caso de las instituciones militares. Posteriormente Espinoza & Jiménez (2007) concluyen que una restricción conocida también como cuello de botella, se define como cualquier elemento que está limitando al sistema en el cumplimiento de la meta para la que fue creado, es decir, para el caso de empresas con fines de lucro, generar ganancias sustentables.

En síntesis, la teoría de restricciones, se centra en el desempeño que desarrollan las restricciones del sistema para establecer mejoras que contribuyan a una meta deseada. Está restricciones pueden ser (i) Físicas, cuando la limitación está relacionada con un factor tangible del proceso de producción. (ii) Mercado, cuando el impedimento está impuesto por la demanda de sus productos o servicios y  (iii) Políticas, cuando la compañía ha adoptado prácticas, procedimientos, estímulos o formas de operación que son contrarios a su productividad. Desde el punto de vista contable, Berrío & Castrillón (2008), establecen que cuando un sistema no puede generar más rentabilidad es porque algo se lo está impidiendo, esto es debido a las restricciones que pueden ser una persona, un equipo, una máquina, una pieza, una política de la empresa, la ausencia de alguna herramienta de apoyo, entre otros.

Por su parte Lee & Plenert (1993), en su trabajo investigativo, indagaron y propusieron iniciativas de cómo se podían incorporar herramientas de modelamiento cuantitativo para la solución de problemas en el ámbito de producción bajo la filosofía de teoría de restricciones. Determinando que cuando se trata de un modelo con numerosas restricciones la programación lineal es superior para encontrar la solución. Más recientemente Sharda & Bury (2010), en su trabajo también establece que para realizar un mejor análisis de restricciones dentro de un proceso productivo, la simulación resulta ser una herramienta eficiente.

El modelo de programación lineal, como en cualquier modelo de investigación de operaciones, tiene tres componentes básicos: las variables de decisión que se trata de determinar, el objetivo (la meta) que se trata de optimizar y las restricciones que se deben satisfacer (Mathur & Solow, 1996). Así mismo al hacer una revisión de la temática  se encontró que Luebbe & Finch (1992) en su estudio proponen aplicar el procedimiento de la teoría de restricciones, usando el enfoque de programación lineal. Tsai et al., (2007) determinaron un algoritmo para optimizar producción que sirvió de herramienta práctica para la programación de los pedidos. Consecuente a esto, Ortiz & Caicedo (2012), diseñaron un plan óptimo  de producción en una planta embotelladora, buscando como objetivo las cantidades optimas de pedido a un menor costo, paralelamente Ortiz (2013) desarrollan una técnicas de optimización basado en teoría de restricciones para diseñar un modelo en una empresa textil, cuyo objetivo principal era el aumento de la productividad, contemporáneamente Caicedo & Ortiz (2014) diseñan un modelo matemático de optimización para mezcla de producción en una empresa de calzado, cuyo era objetivo era la de determinar las cantidades optimas y el orden de los pedidos, más recientemente Cortabarría et al., (2016) diseñan e implementan una metodología para aplicar la teoría de restricciones con consideraciones de optimización para las empresas metalmecánicas.

Por otra parte, un estudio de simulación permite conducir a un mejor entendimiento del sistema y por consiguiente sugerir estrategias que mejoren la operación y eficiencia, a su vez anticiparse a las restricciones o cuellos de botellas o algún otro problema que pueda ser limitante del proceso (Naylor & Kong 1971). Al hacer una revisión de la temática, se encontró que Tsou (2012), exploró algunas técnicas de simulación en la cadena de suministros mediante la aplicación de la teoría de las restricciones con el fin de ajustar los niveles de inventario. Así mismo Herrera (2013), desarrolla la aplicación de la simulación, con el fin de mejorar un proceso caso de estudio, teniendo en cuenta las restricciones dentro del sistema. Consecuente a esto, Sánchez et al., (2015). Desarrollaron un modelo  de simulación del sistema real, logrando identificar las partes de los procesos responsables de atrasos y cuellos de botella,  permitiendo plantear un escenario de solución. Paralelamente Golmohammadi (2015), hizo un estudio de programación de la producción basado en la teoría de restricciones, para esto, diseña una serie de escenarios de simulación que proporcionan información sobre el plan maestro de producción. Contemporáneamente Costas et al., (2015), aplicó de la teoría de restricciones para reducir el efecto Bullwhip en la gestión de las cadenas de suministros a través del modelado se simulación basado en agentes. Más recientemente Hussain et al., (2016), Investigaron de igual forma la seguridad el efecto Bullwhip en una cadena de suministros mediante experimentos de simulación, teniendo en cuenta el impacto de las restricciones de capacidad y de inventarios.

Un diagnóstico inicial en la empresa caso de estudio, mediante herramientas de evaluación rápida de planta planteado por Goodson (2002)  y del modelo referencial en logística propuesto por Feres (2014) logró evidenciar que existe un alto porcentaje en el incumpliendo de los pedidos, debido de los bajos volúmenes de producción, afectando las  entregas a tiempo de los productos solicitados. Por consiguiente se brindan instancias habilitadoras para poder llevar a cabo como objetivo el identificar la restricción del proceso productivo con apoyo de la optimización aplicando un modelo de programación lineal y de simulación programando los diferentes modelos en ProModel , que sirvan de apoyo para la toma de decisiones y beneficio para la rentabilidad de la empresa.

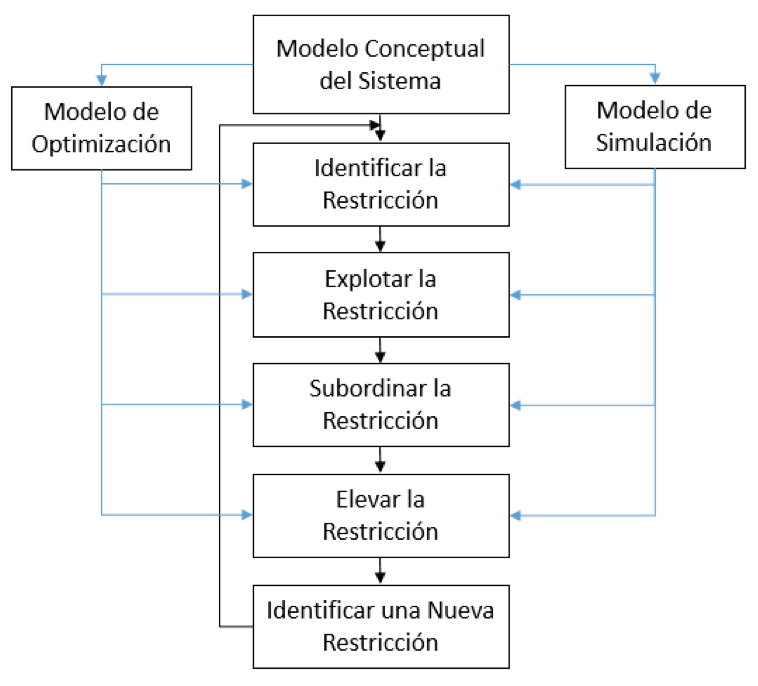
Con la finalidad de identificar la restricción del sistema se tomó como referencia la metodología planteada por Goldratt & Cox (1993), la cual se componen de cinco pasos como son: (I) Identificar la restricción o cuello de botella del sistema. (ii) Explotar la restricción para maximizar su utilidad. (iii) Subordinar el resto del sistema a la restricción. (iv) Elevar la restricción o aumentar la capacidad del cuello de botella, para esto se hace necesario desplazar partes a otros procesos, aumentar las horas-hombres, aumentar maquinaria o subcontratando parte de la producción. (v) Identificar una nueva restricción una vez se roto la restricción anterior. Con base a lo anterior en la figura 1 se propone una metodología con consideraciones de optimización y simulación que permitan determinar y analizar los indicadores de desempeño y los costos de operaciones en cada uno de los pasos, soportando el mejoramiento del sistema, la toma de decisiones y los mayores beneficios para la empresa.

Figura 1
Propuesta metodológica a partir de Goldratt & Cox (1988)

2.1. Modelo conceptual del sistema

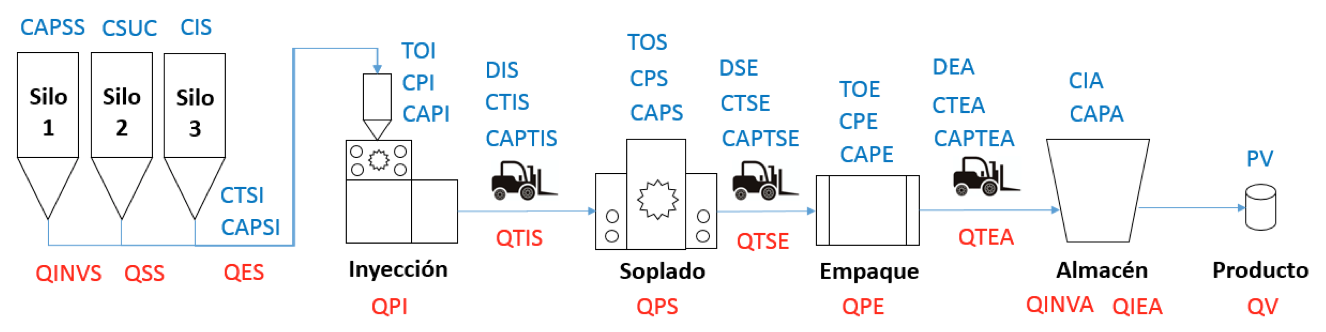
La empresa caso de estudio desarrolla productos a base de polietileno y pet, trabajan mano a mano con sus clientes para generar mejores productos, impactando la vida de las personas y convirtiéndose en una pieza esencial para el desarrollo económico del país. Dentro de su portafolio sobresale la línea de producción de productos transparentes, la cual se encuentra conformada por cinco fases, como son los silos (3), la inyectora (1), la sopladora (1) y el área de empaque y almacenamiento de productos.

A partir de visitas periódicas y la técnica de observación del proceso productivo de esta línea en la empresa caso de estudio, se hicieron mediciones de tiempo, distancia  y capacidad de cada una de las operaciones que lo componen. Adicional a esto se diligenciaron los parámetros para el desarrollo de los modelos de optimización y de simulación que permitirán analizar y encontrar la restricción del sistema (Ver figura 2).

Figura 2
Modelo conceptual del sistema

2.2. Modelo de optimización

Los supuestos para poder llevar a cabo el modelo de optimización son: (i) Los inventarios iniciales de los silos en cualquier periodo de tiempo es de 2000 kg. (ii) Los inventarios iniciales del almacén de productos terminados es de 1000 kg. (ii) Las labores de producción se desarrollan durante las 24 horas del día (iii) Los periodos de tiempos están dados en meses y se trabajan todos los días. (v) Cada una de las estaciones de trabajo se dedican a una operación en particular. (vi) Los inventarios por estación son ilimitados.

En el proceso productivo del caso de estudio interviene una planta conformada por “s” silos de almacenamiento que pueden producir durante un horizonte de tiempo “t”. A partir de esto se declaran cada uno de los conjuntos necesarios para la construcción del modelo:

s                Silos de almacenamiento             (s: 1,2,3)               

t                Periodo de tiempo                            (t: 1,2,3,4,5,6)

Se describen los parámetros del modelo propuesto, los cuales están ligados con las limitaciones de capacidad, los tiempos de operaciones, distancias entre estaciones de trabajo, costos de producción, costo de transporte, costo de inventario y precio del producto. 

CAPSS                     Capacidad de succión en los silos por día en Kgs

CAPSI                       Capacidad de transporte desde silos a la inyectora en Kgs

CAPI                         Capacidad de la inyectora por día en Kgs

CAPS                        Capacidad máxima de la sopladora por día en Kgs

CAPE                        Capacidad máxima de empaque por día en Kgs

CAPA                        Capacidad máxima de del almacén en Kgs

CAPTIS                    Capacidad de transporte de inyectora a sopladora en Kgs

CAPTSE                   Capacidad de transporte de sopladora a empaque en Kgs

CAPTEA                   Capacidad de transporte de empaque a almacén en Kgs

PV                          Precio de venta del producto en Kgs

CSUC                        Costo de succión por Kgs

CTSI                         Costo de transporte de silos a inyectora en Kgs

CTIS                         Costo de transporte de inyectora a sopladora en Kgs

CTSE                        Costo de transporte de sopladora empaque en Kgs

CTEA                         Costo de transporte de empaque a almacén en kgs

CPI                            Costo de producción en inyectora de una unidad de producto en Kgs

CPS                           Costo de producción en sopladora de una unidad de producto en Kgs

CPE                           Costo de producción en empaque de una unidad en Kgs

CIS                             Costo de inventario en silos por Kgs

CIA                            Costo de inventario en almacén por Kgs

FISEG                       Factor de inventario de seguridad

TOI                            Tiempo de operación de Invectora en min

TOS                           Tiempo de operación de sopladora en  min

TOE                           Tiempo de operación de empaque en min

DIS                            Distancia de inyectora a sopladora en mts

DSE                           Distancia de sopladora a empaque en mts

DEA                           Distancia de empaque a almacén en mts

Las variables del modelo propuesto están ligadas a las cantidades que se deben producir y transportar en cada una de las estaciones de trabajo, las cantidades a almacenar y las cantidades a vender en un periodo de tiempo t. A continuación, se declaran las variables del modelo:

QSS(s,t)                   Cantidad a succionar en los silos en un periodo t

QES(s,t)                   Cantidad a extraer en los silos en un periodo t

QPI(s,t)                   Cantidad a producir en inyectora en un periodo t

QTIS(s,t)                 Cantidad a transportar desde inyectora a sopladora en  un periodo t

QPS(s,t)                  Cantidad a producir en sopladora en un periodo t

QTSE(s,t)                Cantidad a transportar desde sopladora a empaque en un periodo t

QPE(s,t)                  Cantidad a producir en empaque en un periodo t

QTEA(s,t)               Cantidad transportada de empaque a almacén en un periodo t

QINVS(s,t)             Cantidad de inventario en los silos en un periodo t

QINVA(s,t)            Cantidad de inventario en almacén en un periodo t

QIEA(s,t)                Cantidad  que entran al almacén que vienen de empaque en un periodo t

QV(s,t)                    Cantidades vendidas en el periodo t

La función objetivo de la empresa caso estudio consiste en maximizar sus utilidades brutas.  La ecuación [1], muestra la formulación matemática que representa la forma de calcular las utilidades totales producto de las ventas y los costos asociados a la producción y manipulación.

Se establecen cada una de las limitaciones del modelo, las ecuaciones [2] a [7] representan las restricciones asociadas a la capacidad de cada una de las estaciones de trabajo, las ecuaciones [8] a [11] son las restricciones de capacidad de transporte entre las estaciones, las ecuaciones [12] a [18] son restricciones de equilibrio, las ecuaciones [19] y [20] son de inventario y la restricción [21] de no negatividad.

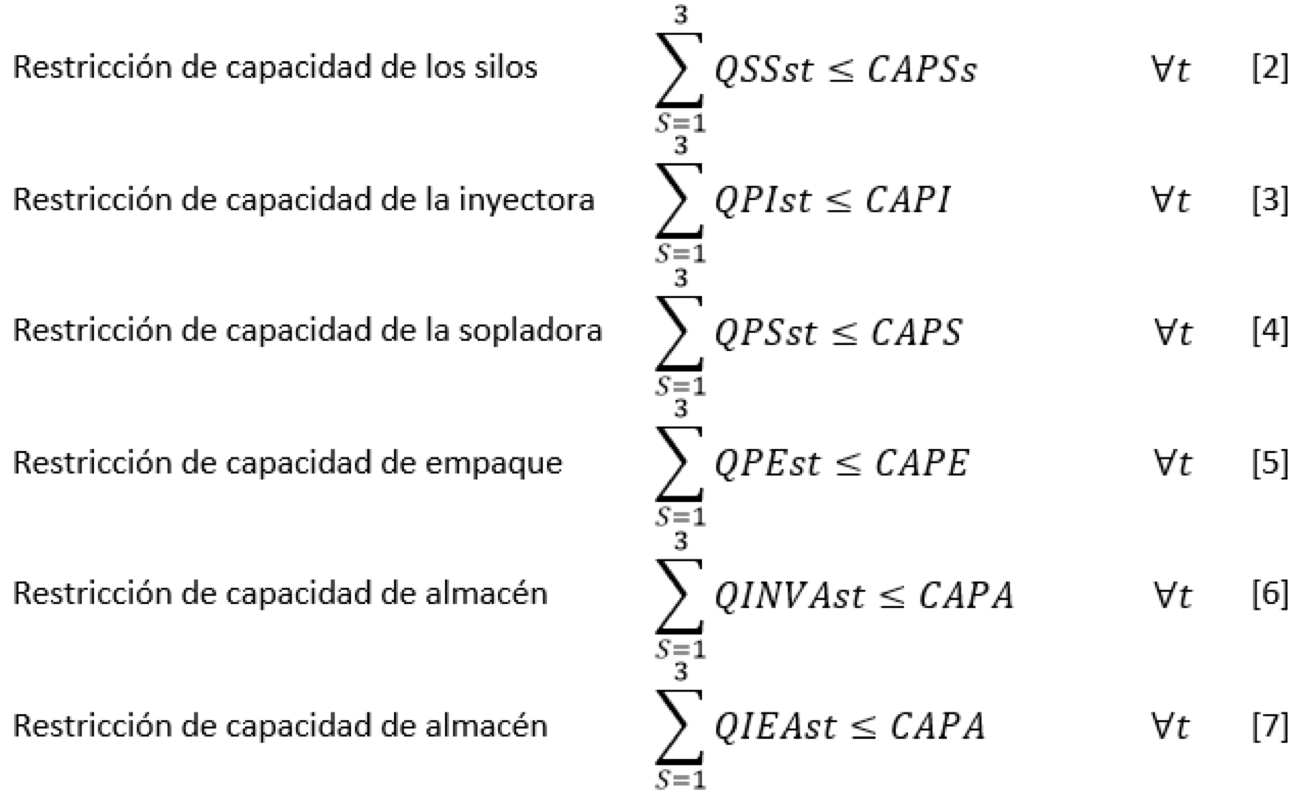
En forma general el modelo genera un total de 216 variables de decisión, de las cuales 18 corresponden a la variable QSS, 18 a la variable QES, 18 a la variable QPI, 18 a la variable QTIS, 18 a la variable QPS, 18 a la variable QTSE, 18 a la variable QPE, 18 a la variable QTEA, 18 a la variable QINVS, 18 a la variable QINVA, 18 a la variable QIEA, a la variable QV, además presenta un total de 222 restricciones en toda la construcción del modelo.

2.3. Modelo de simulación

Para el modelamiento del sistema fue necesario conocer el proceso productivo e identificar los diversos elementos del modelo como las locaciones, entidades, arribos, variables, atributos y secuenciación de las actividades. Para esto se hace necesario de una herramienta o técnica informática que permita analizar el comportamiento de un sistema bajo diferentes condiciones de operación asociadas a las etapas de la teoría de restricciones. Para la realización del estudio se necesitó de una serie de pasos básicos, fundamentados en la metodología planteada por Guash, et al. (2005), donde se debe: (i)  Definir el problema y planificación del estudio. (ii) Recogida de datos. (iii) Formulación del modelo conceptual. (iv) Construcción del modelo. (v) Verificación, validación y pruebas. (vi) Diseño de los experimentos de simulación. (vii) Análisis de los resultados y (viii) Documentación e implementación.

El presente estudio de caso se realizó en una empresa del sector plástico de la ciudad de Cartagena – Colombia. Con el objetivo de determinar el recurso restrictivo del sistema, a partir de un enfoque de teoría de restricciones con consideraciones de optimización y de simulación. Ambos modelos se corrieron en un equipo con características de 10 GB de memoria RAM y un sistema operativo de 64 bits con Windows 7. Para poder determinar las utilidades y el resultado óptimo de las variables se utilizó la ayuda del software GAMS (General Algebraic Modeling System), como su nombre lo indica es un lenguaje de modelización, más que un programa para resolver problemas de optimización. Y para el modelo de simulación se utilizó él software ProModel, un programa simulador de procesos industriales de manufacturación.

3.1. Modelo de Optimización

Para poder determinar las utilidades totales y el resultado óptimo de las variables se programó el modelo matemático. A continuación en la figura 3 se evidencia el código de programación de la función objetivo y de las restricciones.

Figura 3
Programación del modelo de optimización en GAMS

La existencia de un cuello de botella o recurso restrictivo en el área de soplado se evidencia claramente con los resultados obtenidos en el modelo de optimización. En la figura 4 se observa que el sistema se encuentra limitado en las cantidades producidas por la sopladora (QPS).  Para este tipo de modelo solo fue posible emplear para el mejoramiento del proceso la etapa de identificación y elevación de la teoría de restricciones. En el modelo de identificación el sistema se encuentra limitado a 7.200 unidades, con un resultado en la función objetivo correspondiente a $1395 USD. Para la ejecución del modelo de elevación, se hace posible poder realizar un cambio en la configuración de la capacidad máxima de la sopladora con un incremento del 50%. Permitiendo un aumento en los productos terminados y un efecto positivo en la función objetivo de $1420 USD.

Figura 4
Resultado de las variables en los modelos de optimización

3.2. Modelo de Simulación

Aplicando la metodología planteada por Guash, et al. (2005) una vez se establecen los objetivos o metas se establece el modelo conceptual con cada uno de los elementos necesarios para poder llevar a cabo la simulación. En la figura 5, evidencia el layout de la planta de producción, junto con las locaciones las variables y los indicadores del modelo.

Figura 5
Modelo conceptual del layout construido en ProModel v9.2

Adicional a esto, para poder determinar las variables e indicadores del modelo se programó el modelo mediante el software ProModel v9.2. A continuación en la figura 6 se evidencia el código de construcción del proceso del modelo.

Figura 6
Modelo construido en ProModel v9.2

Para este tipo de modelo se logró poder aplicar cada una de las fases de la teoría de restricciones. En la primera etapa de identificación se observa que de igual forma la restricción es la estación de trabajo de trabajo sopladora, dado que es capaz de procesar aproximadamente el 60,7% de lo producido por la inyectora.

En la etapa de explotación, teniendo en cuenta que la sopladora puede procesar un máximo de 12000 envases en la jornada de trabajo (24 Hrs) y  que solo se están produciendo 11668 unidades, es predecible decir que aún se pueden llegar a soplar hasta 332 envases más. Dado lo anterior se procede dentro del  modelo a: (i) intervenir al recurso montacargas variando su velocidad de trabajo según la normatividad establecida teniendo en cuenta variables como peso y volumen (Ledezma & Yoma, 2014; INS, 2012; Vásquez, 2013). (ii) Crear un arribo de 335 cantidades de la entidad preformas en la locación de soplado una única vez al inicio de la corrida. (iii) Incluir las unidades de preformas que arriban directamente al área de soplado en el indicador productos en espera (WIP). Logrando así un aumento en el throughout (TH) en su valor promedio en 11,64% pasando de 7,03 a 7,96 unidades terminadas por minuto, aumentar la cantidad de producto terminado (PT) y de unidades sopladas en más del 5% cada uno en su valor promedio mientras que en el valor final pasaron de 11668 a 11991 unidades, es decir 2,69% más.

Para la siguiente etapa se prosigue a subordinar las demás estaciones de trabajo de acuerdo a la capacidad de la sopladora, de acuerdo a los resultados obtenidos, se observa que el tiempo de la inyectora a las 15 horas de haber iniciado la corrida se han producido poco más de 12000 preformas, que es la capacidad diaria de la sopladora. Mientras que en empaque las dos primeras horas es de baja actividad y posteriormente comienza a generar picos altos intermitentes. De acuerdo a esto, los cambios planteados al modelo de simulación son: (i) Crear un tiempo muerto en la locación inyectora que ordene a la locación trabajar solo 15 horas durante la corrida. (ii) Crear un tiempo muerto en la locación empaque que al arrancar la simulación evite que esta área este activa durante las dos primeras horas de corrida. Los resultados evidencian una reducción en los inventarios de productos en procesos (WIP) quedando en 1035 unidades en proceso de las 7600 unidades que se lograban en el proceso original. Las unidades sopladas llegan al máximo posible de 12000 envases y los productos terminados a 11800 unidades. En términos de costos se presenta una reducción en los costos de inyección en 60% y en transporte son 50,51%, dado que no se hace necesario seguir transportando preformas que no serán sopladas.

En la etapa de elevación. Se toma como base los resultados obtenidos en el modelo de explotación. Puesto que en el de subordinación, se redujo la cantidad de producción de la inyectora. El cambio que se requiere es agregar una unidad en la estación de sopladora. Los resultados  evidencian cambios significativos, en el throughout (TH) pasando de 7,03 a 12,48 unidades terminadas por minuto, el tiempo de ciclo (TC) se da una disminución de llegando a 58,03 minutos por unidad, es decir 241,99 minutos menos. Otra mejora es el aumento de 7200 unidades más de productos terminados (PT) logrando un total de 18800 unidades.

Figura 7
Resultado en los modelos de simulación

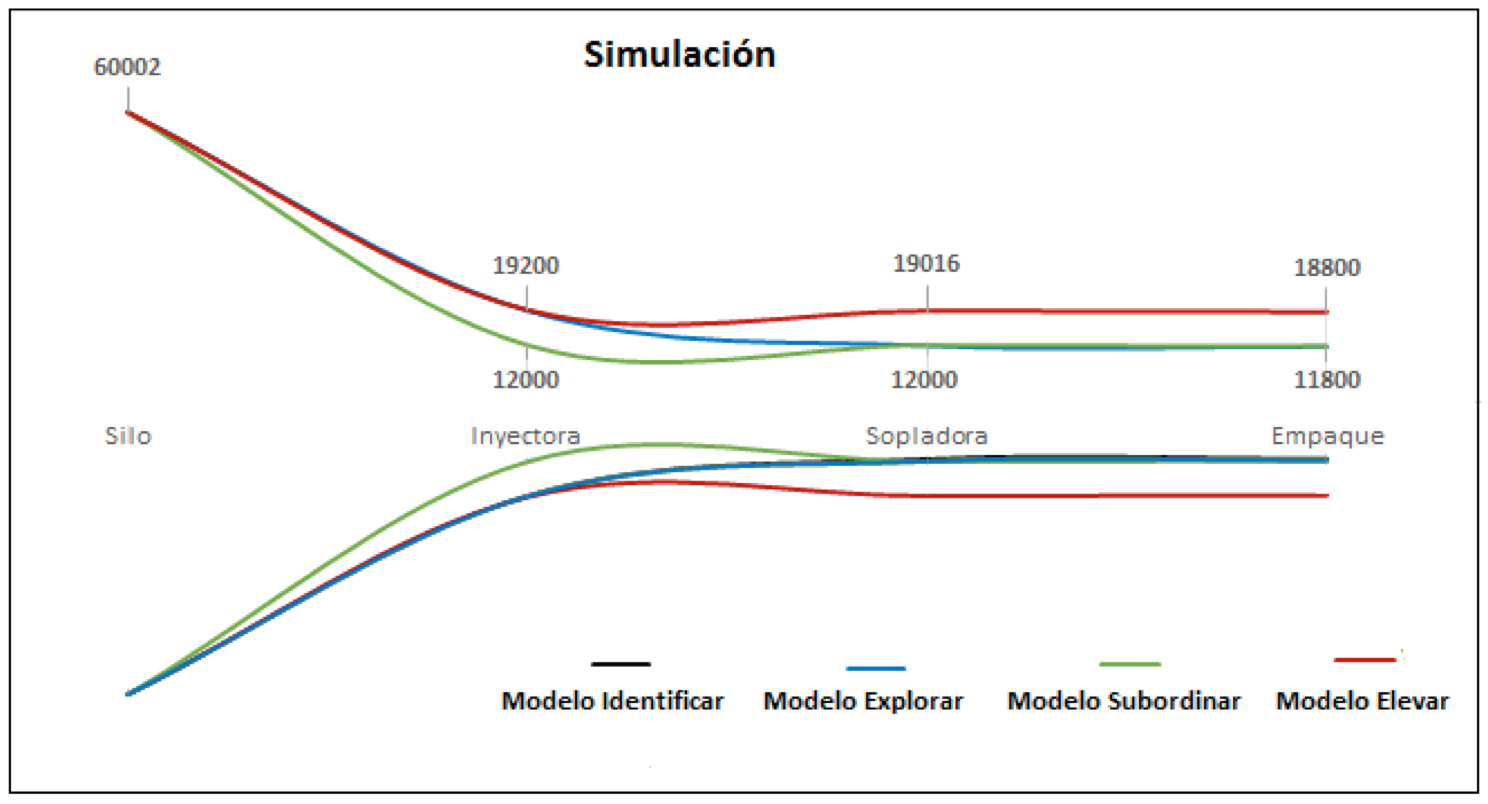
En la figura 7, se puede observar que el modelo elevar presenta mejor resultado en los indicadores del sistema, a su vez se puede evidenciar que el nuevo cuello de botella o recurso restrictivo está ubicado en la estación de inyección, sin embargo si se tiene en cuenta que la inyectora esta un 94% del tiempo vacía y que adicionalmente no se lograron cambios en los indicadores de inventario de los silos y de las unidades producidas en la inyectora, la nueva restricción está dada por el transporte de los silos a la inyectora, dado que esta pueden aprovechar las entradas de materia prima y la capacidad de este proceso.

Analíticamente la aplicación de la simulación y la optimización en esta investigación permitió obtener resultados similares con respecto a la identificación de cuellos de botella, siendo ambas técnicas de mejora con alcances muy diferentes,  comparando la calidad de respuesta de ambos modelos, se puede analizar que el modelo de optimización permite obtener la mejor alternativa entre un abanico de posibilidades, a diferencia del modelo de simulación que no permite llegar a resultados óptimos, pero logra evaluar el sistema actual con otras variables diferentes y comparar distintos escenarios (Ver tabla 1).

Tabla 1
Resultados en unidades y utilidades de ambos modelos

En un mundo cada vez más competitivo por efectos del crecimiento económico, hay que tomar decisiones con mayor rapidez, es por esto que hoy en día todas las compañías están obligadas a implementar un proceso de mejoramiento continuo exitoso y perdurable, que les garanticen una permanencia y desarrollo en el mercado. La aplicación de la teoría de restricciones permite hacer más flexible el sistema productivo, vender más productos, y aumentar las utilidades que es la meta futura de toda empresa.

En esta investigación se presentó una propuesta metodológica con la finalidad de identificar la restricción del sistema, explotar la restricción para maximizar su utilidad, subordinar el resto del sistema a la restricción, elevar la restricción o aumentar la capacidad del cuello de botella e identificar una nueva restricción. Para esto se hizo necesario de herramientas de optimización y de simulación, mediante la aplicación de soportes informáticos como GAMS y ProModel, se pudo determinar en forma óptima los valores de la función objetivos en diferentes etapas y las utilidades en diferentes escenarios.

En síntesis ambos modelos aportan a la toma de decisiones y dan buenos resultados evidenciados en cada una de las etapas de la teoría de restricciones. Con ambos se logra identificar la restricción del sistema o cuellos de botella, a diferencia que con el modelo de optimización maximiza las utilidades con un incremento del 14,5% con respecto al modelo de simulación en la etapa de elevación. Para futuras investigaciones, se deja el campo abierto para aplicar las estrategias de la etapa explotar y subordinar en ambos modelos que ayude a la mejora del sistema actual con consideraciones de un análisis costo beneficio por la adquisición de nuevos recursos.

BERRÍO, Deysi and CASTRILLÓN, Jaime. Costos para Gerenciar Organizaciones Manufactureras,  Comerciales y de Servicio. Editorial Uninorte. Consectetur adipiscing elit. In eu volutpat odio.2008. ISBN 9789588252759

CAICEDO, Alvaro and ORTIZ, Viviana. Mezcla Óptima De Producción Desde El Enfoque Gerencial De La Contabilidad Del Throughput: El Caso De Una Pequeña Empresa De Calzado. Revistas Javeriana. 2014. Vol. 15 No. 37. p. 69-82.

CORTABARRÍA, Laura., MARTÍNEZ, Sindy and MENDOZA, Oscar. Diseño, Implementación Y

Análisis De Una Metodología Para Aplicar TOC A Empresas Metalmecánicas Con Restricciones Físicas Internas – Caso De Aplicación: Colombia Design. Revista Espacios. 2016. Vol. 37. No. 31. p. 30

COSTAS, José., DE LA FUENTE, David., PINO, Raúl and PUCHE, Julio. Applying Goldratt’s Theory Of Constraints To Reduce The Bullwhip Effect Through Agent-Based Modeling. Expert Systems with Applications. 2015. Vol. 42. No. 4. p. 2049-2060. ISSN 0957-4174.

ESPINOZA, Carlos and JIMÉNEZ, Francisco. Costos Industriales. Editorial Tecnológica de Costa Rica. 2007. ISBN 9977661839

FERES, Sahid. Estudio de la Caracterización de la Logística en Colombia. Servicio Nacional de Aprendizaje- SENA. 2014. Colombia

GOLDRATT, Eliyahu and COX, Jeff. La Meta. Un Proceso de Mejora Continua. México: Ediciones North RiverPress. 1993. ISBN 9788479787189

GOLDRATT, Eliyahu. El síndrome del Pajar. Ediciones Castillo Monterrey. 1998. ISBN 8479781297, 9788479781293

GOLMOHAMMADI, Davood. A Study Of Scheduling Under The Theory Of Constraints. International Journal of Production Economics. 2015. Vol. 165. p. 38-50. ISSN 0925-5273

GOODSON, Eugene. Read a plant fast. Harvard Business Review. 2002. p. 3-25

GUASH, Antonio., PIERA, Miguel., CASANOVAS, Josep and FIGUERAS. Jove. Modelación y Simulación: Aplicaciones A Procesos Logísticos De Fabricación Y Servicios. Editorial UPC. 2005. ISBN 9788498802351

HERRERA, Germán. Mejora en el Proceso de Pruebas de Metales en una Empresa de Servicio de Inspección y Laboratorio Empleando simulación con ProModel. Revista Científica Teknos. 2013. Vol. 13. No. 1. p. 39-54

HUSSAIN, Matloub., KHAN, Mehmood and SABIR, Hussein. Analysis of Capacity Constraints on the Backlog Bullwhip Effect in the Two-tier Supply Chain: a Taguchi Approach. International Journal of Logistics Research and Applications. 2016. Vol. 19. No. 1. p. 41-61

INS, Instituto Nacional De Seguros. Manejo Seguro de Montacargas. Instituto Nacional de Seguros, Gestion Empresarial en Salud Ocupacional. San José: INS. 2012.

LEDEZMA, and YOMA, Emilio. Manejo Defensivo en Montacargas. Trabajo Universitario, Universidad Tecnológica Nacional. 2014.

LEE, Terry and PLENERT, Gerhard. Optimising Theory of Constraints When New Product Alternatives Exist. Production and inventory management journal. 1993. Vol. 34. No. 3.  p. 51-57.

LUEBBE, Richard and FINCH, Byron. Theory Of Constraints And Linear Programming: A Comparison. International Journal of Production Research. 1992. Vol. 30. No. 6. p. 1471-1478.

MATHUR, Kamlesh and SOLOW, Daniel. Investigación de Operaciones. El Arte en la Toma de Decisiones. México: Prentice Hall. 1996. ISBN 9688806986, 9789688806982

MORALES, Julian. Propuesta Para Implementar Un Sistema De Programación De La Producción,  Bajo Teoría De Restricciones, En Una Empresa De Artes Gráficas. Universidad de Antioquia, Medellín, Colombia.2006. p. 69.

NAYLOR, Thomas and KONG, Chu. Técnicas de Simulación en Computadoras. Editora Limusa. ISBN 02159952

ORTIZ, Viviana and CAICEDO, Alvaro. Optimal Production Plan In A Soft Drink Bottling Plant. Revista Ingeniería Industrial. 2012. Vol. 11 No. 1. p. 69-82.

ORTIZ, Miguel. Theory of Constraints and LP Modeling as Strategic Decision Tools for Productivity Increasing in the Towel Line of a Textile-Confection Sector Company. Revista Prospectiva.2013. Vol. 11. No. 1. p. 21-29. ISSN 16928261

SÁNCHEZ, Paola. A., CEBALLOS, Fernando and TORRES, Germán. Análisis Del Proceso Productivo De Una Empresa De Confecciones: Modelación Y Simulación. Ciencia e Ingeniería Neogranadina. 2015. Vol. 25. No. 2. p. 137-150.

SHARDA, Bikram and BURY, Scott. Bottleneck Analysis Of A Chemical Plant Using Discrete Event Simulation. Winter Simulation Conference (WSC). Baltimore, MD. 2010. P. 1547-1555.
Doi: 10.1109/WSC.20105678916

TSAI, W., LAI, C. and CHANG, J. An Algorithm For Optimizing Joint Products Decision Based On The Theory Of Constraints. International Journal of Production Research. 2007. Vol. 45. No. 15. p. 3421-3437.

TSOU, Chi. On The Strategy Of Supply Chain Collaboration Based On Dynamic Inventory Target Level Management: A Theory Of Constraint Perspective. Applied Mathematical Modelling. 2013. Vol. 37. No. 7. p. 5204-5214

VÁZQUEZ, Jesus. Seguridad de Montacargas. 2013. Disponible en la pagina web:  https://paginasprodigy.com.neotecno

1. PhD(c) Ingeniería Mención en Industrial. M.Sc. en Ingeniería con Énfasis en Industrial. Docente investigador de la Fundación Universitaria Tecnológico Comfenalco. Grupo de Investigación CIPTEC. Cartagena-Colombia. Email: herreravg@tecnocomfenalco.edu.co

2. Ingeniero Industrial. Fundación Universitaria Tecnológico Comfenalco. Cartagena–Colombia. Email: jorleocamjuv@hotmail.com

3. Ingeniero Industrial. Fundación Universitaria Tecnológico Comfenalco. Cartagena–Colombia. Email: jhonny.bernalh@gmail.com

4. Ingeniero Industrial. Fundación Universitaria Tecnológico Comfenalco. Cartagena–Colombia. Email: r-tilves17@hotmail.com