ISSN 0798 1015

Vol. 38 (Nº 60) Año 2017. Pág. 36

Análisis comparativo con fines pedagógicos en el diseño de filtros supresores de banda angosta con T gemela y FDNR

Comparative analysis with pedagogical purposes in the design of narrowband suppressor filters with twin-T and FDNR

José Luis SIMANCAS-GARCÍA 1; Carlos SILVA-CÁRDENAS 2; Elkin RAMÍREZ-CERPA 3; Rubén SÁNCHEZ-DAMS 4; Alejandro CAMA-PINTO 5

Recibido: 04/10/2017 • Aprobado: 15/10/2017

Contenido

1. Introducción

2. Metodología

3. Pruebas y Resultados

4. Análisis de los resultados

5. Conclusiones

Referencias bibliográficas

1. Introducción

En la revisión de los contenidos de las asignaturas relacionadas con el diseño de circuitos con amplificadores operacionales (OA, Operational Amplifier) de algunas de las universidades de la región caribe en Colombia (Universidad Antonio Nariño, 2015; Universidad del Norte, 2015; Universidad de la Costa, 2015) donde se enseña ingeniería electrónica (Zamora-Musa, 2017), se encuentra que los convertidores de impedancia no son estudiados, específicamente, los circuitos de resistencia negativa dependientes de la frecuencia (FDNR, Frequency-dependent Negative Resistance) y los giradores (sintetizadores de inductancia o circuitos de Antoniou). Tal situación es comprensible pues en los libros de texto que sirven como guías de la asignatura hay insuficiencias en lo relacionado con estos temas. En el libro de Rashid (Rashid, 2012) no trata el tema de los convertidores de impedancia. En el libro de Sedra (Sedra, 2010) se estudian los circuitos convertidores de impedancia y da una explicación al respecto, pero se limita solo a los giradores y no trata el tema de FDNR, tampoco desarrolla ningún ejemplo sobre su uso en el diseño de filtros activos. Franco (Franco, 2005) es un libro especializado exclusivamente en el diseño de circuitos con OA, pero solo le dedica 6 páginas de sus 680 al estudio de los convertidores generalizados de impedancia y FDNR. Sin embargo, realiza 2 ejemplos de aplicación de los convertidores, uno para el girador y otro para el FDNR. Otros libros de texto utilizados en el ambiente universitario para la enseñanza de la electrónica se revisaron y se encontró que tampoco llevaban a cabo un desarrollo sobre la temática (Horenstein, 1996; Gray and Meyer, 1990; Boylestad and Nashelsky, 2003; Förster, 2015). Una de las dificultades encontradas es la ausencia de publicaciones de los planes de asignatura de las universidades a nivel nacional, impidiendo la generalización de argumento inicial.

La oportunidad surge en el momento en que revisando la literatura se hace evidente que los circuitos FDNR son cada vez más utilizados en distintas aplicaciones, entre las que se destacan 2 específicamente: circuitos caóticos (Elwakil and Kennedy, 2000) y filtros activos (Hickman, 1997). El uso de los circuitos caóticos crece, especialmente debido al surgimiento de los sistemas caóticos de comunicaciones (Corron and Hahs, 1997; Silva and Young, 2000; Stavrinides et al., 2009). Por ello, su estudio ha dejado de ser algo exótico y puramente teórico debido a su extraño comportamiento para convertirse en un dispositivo importante dentro de sistemas prácticos actuales. Desde hace un par de décadas hasta la actualidad, los filtros construidos con base en giradores (Prodanov and Green, 1994) o con FDNR (Hasler, 1980; Kaçar and Kuntman, 2011; Susan, 2012; Mahmoud and Abdallah and Khalid, 2013) han ido en aumento.

Hay literatura adicional en la que se proponen nuevas formas de implementación de los circuitos FDNR y la aplicación de esos nuevos bloques en el diseño de filtros pasa-bajas (Sedlácek and Szabó, 2009), así como un análisis comparativo de las ventajas y desventajas de estas formas de sintetizar los circuitos FDNR (Szabó and Friedl and Sedláček, 2013). También se puede encontrar el caso de implementaciones VLSI (Very Large Scale Integrated) de los circuitos FDNR en donde se estudia el proceso de reemplazar las resistencias utilizadas por transistores MOSFET (Yang and Shiyan, 1991) o el caso de utilizar tecnología basada en condensadores conmutados (Cooperman and Kapral, 1983). Otros artículos muestran la implementación de filtros usando FDNR pero con OA trabajando en modo corriente (Kaçar and Kuntman, 2009), así como el análisis de la función de transferencia de red de un circuito que implementan resistencias negativas (Bruton, 1969). Existen trabajos que realizan discusiones profundas sobre el uso de los circuitos FDNR como el caso de métodos para la realización de filtros y osciladores (Senani, 1979), o análisis de ruido eléctrico en los filtros que los utilizan (Bruton and Treleaven, 1973). Un trabajo introductorio al tema es de Merrill (Merrill, 1950), pero con el inconveniente que fue desarrollado en torno a amplificadores con tubos de vacío, tecnología con la que los estudiantes no están familiarizados haciendo inabordable el tema por parte de los estudiantes.

De lo antes mencionado, se hace necesario un estudio introductorio de los giradores y de los circuitos FDNR adecuado para estudiantes de ingeniería electrónica, con la intención de superar las limitantes encontradas en la literatura y que les permita adquirir destrezas en el diseño de circuitos con OA, y tomas de decisiones de diseño en función de análisis comparativos realizados en torno a las distintas aplicaciones.

En la sección II se presenta la metodología utilizada para introducir por primera vez esta temática al curso de Electrónica II y los resultados consignados en este trabajo. En la sección III se introducen de manera básica pero detallada los convertidores de impedancia, específicamente los giradores y los circuitos FDNR, así como su análisis a partir de la teoría de circuitos. En la sección IV se lleva a cabo el diseño de 2 filtros supresores de banda angosta, uno con T gemela y otro con FDNR. En la sección V se presentan los resultados de las simulaciones de ambos diseños, así como de las mediciones de sus respuestas en los prototipos construidos, para elaborar un análisis comparativo. En la sección VI se presentan las conclusiones.

Se revisó la literatura relacionada con este tema, principalmente del FDNR: los libros, que resultaron insuficientes en el manejo del tema, y los artículos en su mayoría no fueron adecuados para un primer estudio del tema por parte de los estudiantes de ingeniería electrónica. Luego se estudian 2 circuitos convertidores de impedancia, específicamente el girador y el FDNR, y se ampliaron los análisis llevados a cabo por Franco en su libro. Posteriormente se hizo la aplicación de estos conceptos a un diseño práctico.  Se escogió en este caso FDNR, por tratarse del menos estudiado en la literatura, pero de utilidad creciente. Ante la disyuntiva si utilizar el circuito FDNR para construir un sistema caótico o un filtro, los autores se decantaron por la segunda. Como existe en la literatura varios filtros pasa-bajas construidos con FDNR, se prefirió el diseño de un filtro supresor de banda angosta, que son utilizados en equipos biomédicos. Con la intención de estudiar las ventajas y desventajas de este tipo de diseño, se hizo un análisis comparativo de su funcionamiento con el de otro filtro que realizara la misma función, pero utilizando la técnica en T gemela. Ambos diseños, una vez obtenidos teóricamente, se simularon, y los resultados se contrastaron. Posteriormente se construyeron prototipos de ambos diseños para medir físicamente sus respuestas en frecuencia y complementar el análisis previo. Para la construcción de los prototipos se utilizaron condensadores de poliéster, así como resistencias de película de carbón, y el OA LTC1050 (LTC1050, 2016).

2.1. Convertidores de impedancia

Los convertidores de impedancia son circuitos RC activos que tienen la finalidad de simular elementos que dependen de la frecuencia, tales como inductancias, para ser aplicadas en la síntesis de filtros activos. Según los artículos consultados y presentados en la introducción. Los convertidores de impedancia más utilizados son los giradores y los FDNR, sin embargo, la forma como tratan el tema no es la adecuada para estudiantes de pregrado debido a que los autores asumen que el lector está familiarizado con la temática. Por otra parte, los libros de texto presentan carencias en el desarrollo de estos temas, por lo anterior procedemos a presentar los análisis detallados de estos circuitos que pueden ser consultados en el apéndice.

2.2. Giradores (circuito de Antoniou)

Un circuito girador se construye a partir de un circuito convertidor de impedancia positiva. Su principal aplicación es la sustitución de las bobinas en sistemas de audiofrecuencias, en especial, en los casos en los que se necesitan valores elevados de inductancia. El esquemático básico de un circuito girador se presenta en la figura 1.

Figura 1
Diagrama eléctrico de un circuito girador básico (Sedra, 2010)

De la figura 1, la expresión de L es (Sedra, 2010):

 L=CR²                                                        (1)

Donde L esta dado en Henry (H), C en Faradio (F) y R en Ohmio (Ω). Por simplicidad, se hace que  R1=R2=R3=R5. R5 suele ser una resistencia variable para facilitar el ajuste de la inductancia. En esta configuración uno de los bornes de la bobina sintetizada está conectado a tierra. El efecto de “giro” depende de las relaciones de fase. Al ser ambos amplificadores operacionales iguales, es conveniente que conformen el mismo circuito integrado, consiguiendo un buen seguimiento de fase a pesar de las variaciones de temperatura, y se logra que los giradores operen con frecuencias de 50 kHz como máximo.

2.3. Resistencias negativas dependientes de la frecuencia (FDNR, Frequency-Dependent Negative Resistance)

Reordenando los componentes del girador presentado en la figura 1 se puede llegar a un circuito como el de la figura 2 que es un elemento poco común, de comportamiento equivalente a una resistencia negativa y cuyo valor en magnitud depende de la frecuencia de la señal de entrada. Éste valor se calcula por medio de la ecuación:

                  |-R|=1/(2πf)²D                                       (2)

Figura 2
Diagrama del circuito FDNR (Franco, 2005).

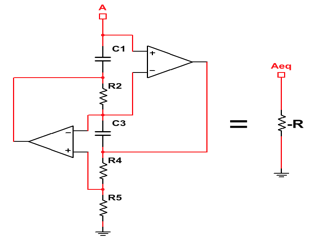
Donde D=R₂R₄C₂C₃/R₅; la frecuencia se expresa en Hz, la resistencia en Ω y la capacitancia en F. A esta ecuación se llega realizando el análisis de circuito análogo del girador anterior.

La aplicación práctica más sencilla es evidente. Conectando una resistencia de igual valor óhmico, pero positiva, al punto A del FDNR, se crea un camino de impedancia nula para una frecuencia determinada.

Teniendo en cuenta que el FDNR está conectada a tierra, y la impedancia del conjunto de ambas es nula, se obtiene, en teoría, un filtro perfecto para dicha frecuencia. En la práctica no es obtenible debido a diferentes desfases, pero agrupando varios filtros de este tipo en cascada pueden conseguirse altos niveles de atenuación.

Este tipo de filtros tienen importantes ventajas sobre otros; por ejemplo, las respuestas en magnitud y fase del filtro de banda eliminada son más estable en frecuencia, y prácticamente independiente de las características del amplificador operacional.

Cuando se diseñan filtros de otro tipo es a menudo necesario recurrir a tablas y ecuaciones complicadas para obtener la respuesta deseada, además de exigir la utilización de inductancias bobinadas, caras, difíciles de obtener y fácilmente perturbable por interferencias externas. Problema que se agudiza si se trata de la realización de un prototipo. El diseño se simplifica al incluir elementos de resistencia negativa, que adecuadamente dispuestos permiten conseguir las características de corte y rechazo requeridas sin que estas se vean afectadas de manera importante por el envejecimiento de los componentes.

No todo son ventajas, la realización de filtros con elementos de resistencia negativa también tienen algunos inconvenientes. En primer lugar, grupos de componentes conectados directamente a elementos de resistencia negativa llegan a emular el comportamiento de componentes pasivos, tales como bobinas, como es el caso de giradores de Antoniou. Para el acoplamiento de la señal a cada sección de resistencia negativa suele ser necesario emplear alguna resistencia o condensador de pequeño valor, debido a la transformación de elementos antes mencionada. En segundo lugar, los amplificadores operacionales exigen un camino de corriente continua a tierra para que la polarización sea correcta. Si se emplean valores bajos de resistencia, pueden presentarse efectos inductivos, pero si se utiliza un valor elevado este efecto es despreciable y puede reducirse para mejorar la respuesta en las frecuencias más bajas. A continuación, se presenta el diseño de un filtro supresor de banda angosta realizado con resistencia negativa.

2.4. Diseño de filtro supresor de banda angosta

A menudo se le conoce como filtro de ranura, y normalmente es utilizado en instrumentos de comunicación y en equipos biomédicos para suprimir frecuencias indeseables, como puede ser las interferencias de líneas de alimentación eléctrica de 60 Hz. Para el caso de este trabajo, la frecuencia a eliminar es de 2.8 kHz, y se escogió de manera arbitraria (Sedra, 2010).

2.5. Filtro supresor de banda angosta con FDNR

La idea con este diseño es construir un filtro supresor de banda angosta, y éste último no es más que un filtro pasa todo que elimina una frecuencia específica. Por simplicidad de diseño, el filtro pasa todo se consigue a partir de uno pasa altas de primer orden (condensador y resistencia en serie) con una muy baja frecuencia de corte. Para tal fin, se adaptó el circuito pasa bajas presentado en el libro de Sedra para un filtro pasa altas en el que se utiliza un simulador de inductancia (Circuito de Antoniou) conectado al nodo central del mismo, en el que se modifica este último bloque por un circuito FDNR y una resistencia en serie de valor igual a la resistencia negativa, con la intención de llevar el nodo central a tierra en la frecuencia que se desea eliminar a través de un camino de resistencia cero (Sedra, 2010). Otra modificación es la eliminación de la etapa de ganancia, y la inclusión de amplificadores operacionales en configuración seguidor de voltaje en la entrada y la salida, para evitar problemas de adaptación de impedancia. La frecuencia de corte del filtro pasa alta viene dada por los valores de la resistencia de 820 kΩ y el condensador de 33 nF, siguiendo la ecuación típica de estos filtros para la especificación en cuestión, f0=1/2πRC. Los elementos de circuito utilizados, ya mencionados, se escogieron de manera arbitraria y por facilidades de adquisición en el mercado local de partes. La frecuencia de corte conseguida fue f0=5,88 Hz, que resulto adecuada para considerar el filtro como pasa todo en un rango de frecuencia de observación de poco más de 4 kHz. El circuito resultante se presenta en la figura 3.

Figura 3
Filtro supresor de banda angosta con FDNR

En el artículo de Biolek y otros, se puede ver la importancia y vigencia que aún tiene el procesamiento analógico de señales (Biolek and Senani and Biolkova and Kolka, 2008), y las nuevas tendencias apuntan a técnicas relacionadas con el trabajo en modo corriente de filtros y otros bloques funcionales analógicos. Sin embargo, en el artículo de Susan (Susan and Jayalalitha, 2010) se evidencia también la tendencia a seguir trabajando en el diseño de filtros usando simuladores de impedancia. Dentro de esta área de trabajo se pueden destacar el diseño de filtros usando circuitos FDNR, como se hace evidente en el artículo de Mahmoud y otros (Mahmoud and Abdallah and Khalid, 2013), que muestra una aplicación moderna de este tipo de filtros. La ecuación a emplear es (2) la cual se deduce en el apéndice:

|-R|=1/(2πf)²D                                                        (3)  

El valor absoluto de D es:

D=1/((2πf)²|-R|)                                                      (4)

Sustituyendo por los valores reales:

D=1/((2×π×2,8kHz)²×10k Ω)=3,23 ×10^-3                 (5)

A continuación, deben elegirse valores para R4, R5, C1 y C3. R4 y R5 deben ser iguales entre sí y al valor absoluto de la resistencia negativa que se piensa conseguir. C1 y C3 deben ser condensadores de poliéster, que permitiría conseguir un factor de calidad Q más elevado y porque en ese material se consiguen valores de capacitancia menores, por su baja constante dieléctrica. Las corrientes de fuga no se consideran un problema, pues los voltajes a los que van a estar sometidos los condensadores no son elevados. Se recomienda utilizar condensadores de 10 nF. Queda por calcular R2.

R₂=(D×R5)/(R₄×C₁×C₂)                                            (6)

El valor más próximo entre los normalizados de uso corriente es 3,3 kΩ.

2.6. Filtro supresor de banda angosta con T gemela

En esta sección se diseñará un filtro supresor de banda angosta usando una T gemela que es comúnmente utilizado en diversas aplicaciones como filtro (Lu et al., 2011). En el caso que nos ocupa se utilizará para eliminar una frecuencia de 2,8 kHz, igual que en el caso anterior para FDNR, y para tal fin se usará como guía el diseño del libro de texto de Rashid (Rashid, 2012). En la figura 4 se puede observar el diagrama eléctrico de este tipo de filtro.

Figura 4
Filtro Supresor de Banda Angosta con T Gemela (Rashid, 2012)

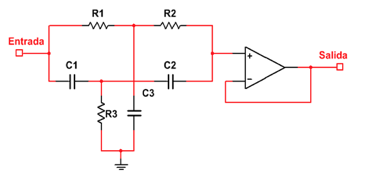
Debido al amplio uso de este tipo de filtro es lógico que este bien documentado y por ende no se profundizará aquí en demostraciones y análisis relacionados, por ejemplo, la función de transferencia, y solo se utilizarán los resultados presentados en el libro antes citado para el cálculo de sus componentes. Los valores de las resistencias de este circuito son R1 = R2 = R y R3=R/2, y los valores de los condensadores son C₂ = C₂ = C y C₃ = 2C. La relación de estos valores de componentes y la frecuencia que se desea suprimir es la siguiente:

 f_N=1/(2πRC)                                                           (7)

Para el caso de la frecuencia de 2,8 kHz, lo valores de R y C obtenidos son 1,2 kΩ y 47 nF, respectivamente, y de aquí se pueden deducir los valores específicos de los componentes del circuito.

Las pruebas para la verificación del correcto funcionamiento de los diseños, se hizo en 2 fases: la primera consistió en hacer simulaciones de los circuitos y la segunda en la construcción de los prototipos y realización de las medidas pertinentes.

3.1. Simulaciones

Para llevar a cabo las simulaciones de los filtros obtenidos, se utilizó el programa de simulación de la empresa Linear Technology LTSpice IV. Para los componentes pasivos de ambos circuitos se utilizaron los estándares que trae el simulador y de comportamiento ideal, pero que ofrecen una buena aproximación al funcionamiento real de los circuitos con valores iguales a los obtenidos en la etapa de diseño. Para el caso de los componentes activos, se escogió de la librería del simulador el amplificador operacional LTC1050, que también sería utilizado durante la implementación física del prototipo. Se escoge este amplificador operacional, porque ofrece un funcionamiento cercano al del amplificador operacional 741, dispositivo ampliamente estudiado en clases. Para verificar que los filtros habían sido bien diseñados, se corrió una simulación tipo Análisis AC, con un barrido de frecuencia lineal desde 0 Hz hasta los 4 kHz, que tiene respuesta en la frecuencia con magnitud calculada en dB y la fase.

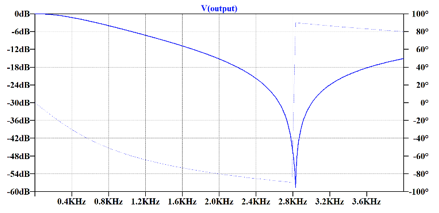
El resultado obtenido del filtro supresor de banda angosta con T gemela se presenta en la figura 5. La máxima atenuación que se consigue es de -58,5 dB a una frecuencia de 2,83 kHz. Se observa en la gráfica que el filtro no presenta una respuesta en frecuencia lo suficientemente angosta para atenuar específicamente la frecuencia de interés sin afectar otras frecuencias dentro de la banda de operación de una aplicación en particular. Por ejemplo, la frecuencia de 60 Hz presente en los equipos médicos (electrocardiograma). Desde la frecuencia de 0,8 kHz se experimentan atenuaciones de -3 dB, es decir, se reducen a la mitad las amplitudes de las señales que están a su alrededor, lo que puede ser indeseable en algunas aplicaciones (Quinayas et al., 2012). La banda encima de la frecuencia eliminada tiene la pendiente de la respuesta en magnitud menor a la observada en la banda inferior, significando que las señales que están por encima de la frecuencia a eliminar experimentarán una atenuación considerable, que puede ser indeseable a nivel de aplicación. Esto obligará, dependiendo del uso del filtro, a la utilización de posteriores etapas de amplificación para esas frecuencias. Obsérvese que, en el rango de frecuencia de 4 kHz, la atenuación no regresa los –3 dB. A los 4 kHz se alcanza -15,12 dB.

Figura 5
Respuesta en frecuencia en magnitud y fase de un
filtro supresor de banda angosta con T gemela.

En la figura 6, el resultado del filtro supresor de banda angosta con FDNR, tiene su máxima atenuación de -25,95 dB a una frecuencia de 2,75 kHz. Es evidente observar que su banda de atenuación es más estrecha y selectiva en comparación con la exhibida por el filtro con T gemela. Se comienzan a experimentar atenuaciones de -3 dB en la banda inferior y superior a 3,01 kHz en las cercanías de la frecuencia de 2,53 kHz, recuperando el mismo nivel de atenuación debido a la simetría de la respuesta en magnitud. Lo anterior significa que las señales que estén en toda la banda alrededor de la frecuencia eliminada, pasaran sin atenuación significativa. A la frecuencia de 4 kHz se han recuperado niveles de atenuación por encima de -1 dB.

Figura 6
Respuesta en frecuencia en magnitud y fase de un filtro supresor de banda angosta con FDNR.

La conclusión a la que se llega luego de observar estas simulaciones es el compromiso que existe entre el ancho de la banda suprimida y el nivel de atenuación conseguido en la frecuencia que se aspira a eliminar. En el filtro con T gemela se consigue un nivel de atenuación mayor en detrimento de una baja selectividad en frecuencia. Por su parte, en el filtro con FDNR, se consigue una selectividad mayor en detrimento de un menor nivel de atenuación en la frecuencia eliminada.

3.2. Mediciones

Una vez construidos los prototipos para los filtros, se procedió a hacer mediciones que permitieran verificar el funcionamiento de los circuitos. Para llevar a cabo tales mediciones se utilizaron los siguientes equipos: generador de señales BK-PRECISION 4011, osciloscopio BK-PRECISION 2120B y fuente de alimentación dual BK-PRECISION 1743. Se utilizó el generador de señales para obtener una señal sinusoidal de 4 VP-P a una frecuencia de 100 Hz. Esta señal fue ingresada a cada uno de los filtros, y se midió la salida con el osciloscopio y se registró. De esta manera se fueron realizando incrementos de 100 Hz en la señal de entrada hasta lograr un barrido de 4,7 kHz. En cada caso se medía la salida con el osciloscopio y se registraba. La magnitud en dB de la respuesta en frecuencia para cada valor de frecuencia se calculó utilizando la siguiente formula:

 Magnitud(dB)=20log(voltaje medido en la salida/4Vp-Vp)          (8)

Los resultados obtenidos para cada uno de los filtros se presentan en la figura 7 de manera conjunta. Para el caso del filtro supresor de banda angosta con T gemela, el máximo nivel de atenuación logrado fue de -33,97 dB y se alcanzó a una frecuencia de 2,8 kHz. Se evidencia en la gráfica el bajo nivel de selectividad de este circuito y la asimetría en las pendientes de la respuesta en frecuencia junto a la frecuencia eliminada. La atenuación conseguida en la frecuencia eliminada es inferior a 24 dB obtenida en la simulación. También se observa que a la frecuencia de 0,7 kHz la atenuación del filtro es de -3 dB, y en la banda superior a la frecuencia eliminada no regresa a esos niveles de atenuación.

Figura 7
Magnitud de la respuesta en frecuencia medida de un filtro
supresor de banda angosta con T gemela y con FDNR

En el caso del filtro supresor de banda angosta con FDNR, la máxima atenuación conseguida fue de -0,45 dB a una frecuencia de 2,4 kHz. Se verifica también un mayor nivel de selectividad en frecuencia de este circuito, y la simetría que hay en las pendientes de la respuesta en frecuencia a los lados de la frecuencia eliminada. La diferencia entre la máxima atenuación conseguida en la simulación y la medida en el circuito real es de más de 15 dB. Cabe resaltar que estas atenuaciones máximas no se consiguen a la misma frecuencia. Por otro lado, la atenuación de -3 dB se consigue a la frecuencia de 2,2 kHz para la banda inferior, y de 2,8 kHz para la banda superior.

Los resultados se analizarán a partir del contraste entre las respuestas simuladas de los filtros y sus respuestas reales medidas en los prototipos. En ambas simulaciones se observa que la frecuencia de máxima atenuación no es exactamente la que se desea eliminar (2,8 kHz), debido a la sensibilidad a los valores de los componentes pasivos de los filtros, que luego de ser calculados se aproximaron a los valores de los componentes físicos más cercanos posibles que se iban a usar en los prototipos. En el caso del filtro con T gemela la desviación fue de 0,03 kHz, lo que se puede considerar aceptable en aplicaciones que no requieran mucha exactitud. Para el caso del filtro con FDNR la desviación fue de 0,05 kHz, también aceptable para aplicaciones que la exactitud no es un requisito clave. Si la exactitud es requerida, se deben colocar componentes variables que permitan hacer ajustes al circuito final, y de esa manera llegar a la respuesta deseada.

Respecto a la especificación de la componente de frecuencia a eliminar, las mediciones realizadas al prototipo arrojan resultados llamativos. Durante las pruebas, la resolución del barrido de frecuencia escogida fue de 0,01 kHz para capturar las desviaciones. En el filtro con T gemela, la atenuación máxima ocurrió en 2,8 kHz, y en el filtro con FDNR a 2,4 kHz. Esta desviación se corrige introduciendo R5 como una resistencia variable que permita hacer los ajustes correspondientes. En cualquier caso, ambos filtros en sus respuestas reales presentan tendencias que se aproximan a las obtenidas en las simulaciones.

Desde la perspectiva del nivel de atenuación conseguido en la frecuencia a eliminar, para el filtro con T gemela, la diferencia entre la respuesta simulada y la medida de más de 24 dB, se debe a la aparición de componentes parásitos en el prototipo físico que se adhieren a componentes pasivos y modifican sus valores nominales, impactando el factor de calidad Q, y por ende afectando negativamente la magnitud de la respuesta en frecuencia, más específicamente en la frecuencia a eliminar. Para el filtro con FDNR, la diferencia de más de 15 dB a la frecuencia atenuada entre la simulación y la medición de la respuesta, se debe a los componentes parásitos y tolerancias de los dispositivos, que inciden en el funcionamiento del circuito de resistencia negativa, desviando su valor, provocando que no exista anulación total con la resistencia de 10 kΩ. Por tanto, la trayectoria a tierra tiene una resistencia distinta de cero, aunque de valor mínimo.

Nuestro trabajo brinda una herramienta a estudiantes de ingeniería para aprender a diseñar soluciones con OA usando giradores y FDNR a través del análisis comparativo de 2 circuitos funcionalmente iguales, pero de técnicas de implementación distintas. Las diferencias entre la respuesta real de un circuito y su comportamiento teórico (y simulado), aparecen por los fenómenos llamados parásitos, y no contemplados durante el diseño teóricos y simulaciones. Con nuestro trabajo, los docentes de la asignatura de circuitos con OA podrán introducir la temática de los giradores y circuitos FDNR en sus cursos además de facilitar el desarrollo de competencias de diseño de circuitos con OA.

Biolek, D., Senani, R., Biolkova, V., and Kolka, Z. (2008). Active elements for analog signal processing: Classification, review, and new proposals Radioengineering. 17(4):15–32.

Boylestad R. L. and Nashelsky L. (2003). Electrónica: teoría de circuitos y dispositivos electrónicos. México: Pearson Educación

Boylestad, R. L. (2013). Introductory Circuit Analysis. Pearson Education, Limited.

Bruton L. T. (1969). Network Transfer Functions Using the Concept of Frequency-Dependent Negative Resistance. IEEE Trans. Circuit Theory. 16(3):406–408.

Bruton V. and Treleaven D. (1973). Electrical noise in low-pass FDNR filters. Circuit Theory, IEEE Trans. 20(2):154–158.

Cooperman M. and Kapral C. W. (1983), Integrated switched-capacitor FDNR filter. Solid-State Circuits, IEEE J. 18(4):378–383.

Corron, N. J., and Hahs, D. W. (1997). A new approach to communications using chaotic signals. Circuits Syst. I Fundam. Theory Appl. IEEE Trans. 44(5):373–382.

Elwakil, A. S., and Kennedy, M. P. (2000). Chaotic oscillator configuration using a frequency dependent negative resistor. Int. J. circuit theory Appl. 28(1):69–76.

Förster, A., Udugama, A., Görg, C., Kuladinithi, K., Timm-Giel, A., Cama-Pinto, A. A novel data dissemination model for organic data flows (2015) Lecture Notes of the Institute for Computer Sciences, Social-Informatics and Telecommunications Engineering, LNICST, 158, pp. 239-252. DOI: 10.1007/978-3-319-26925-2_18

Franco S. (2005). Diseño con amplificadores operacionales y circuitos integrados analógicos. 3ra ed. McGraw-Hill.

Gray P. R. and Meyer R. G. (1990). Analysis and design of analog integrated circuits. 2a ed. New York: John Wiley and Sons, Inc.

Hasler M. (1980). A new class of RC-active filters using FDNR-elements and generalized terminations. Circuits Syst. IEEE Trans. 27(7):636–641.

Hickman I. (1997). Filters using negative resistance. Electron. World Wirel. World. 103(1731):217–223.

Horenstein M. N. (1996). Microelectronic Circuits and Devices. 2a ed. New york: Prentice Hall.

Kaçar F. and Kuntman H. (2009). On the realization of the FDNR simulators using only a single current feedback operational amplifier. In International Conference on Electrical and Electronics Engineering, ELECO. II-223-II-226.

Kaçar F. and Kuntman H. (2011). New realization of FDNR and sixth order band pass filter application. In 20th European Conference on Circuit Theory and Design (ECCTD). 381-384.

LTC1050. (2015). Linear Technology, LTC1050 datasheet. Recuperado el 10 de abril de 2016, de, http://cds.linear.com/docs/en/datasheet/1050fb.pdf.

Iu, H.H.C., Yu, D.S., Fitch, A.L., Sreeram, V., Chen, H. Controlling chaos in a memristor based circuit using a twin-T notch filter (2011) IEEE Transactions on Circuits and Systems I: Regular Papers, 58 (6), art. no. 5688203, pp. 1337-1344. DOI: 10.1109/TCSI.2010.2097771.

Mahmoud, S., Abdallah, A., Khalid, S. A 5.2nV/√Hz noise density third-order FDNR filter for DVB-H mobile-TV receiver (2013) Proceedings of the IEEE International Conference on Electronics, Circuits, and Systems, art. no. 6815520, pp. 739-742. DOI: 10.1109/ICECS.2013.6815520.

Merrill, j. l. (1951). Theory of the negative impedance converter. Bell Syst. Tech. J., vol. 30(1):88–109.

Prodanov, V. I., and Green, M. M. (1994). A current-mode FDNR circuit element using capacitive gyrators. In IEEE International Symposium on Circuits and Systems(ISCS). 5:409-412.

Quinayas C., Fabian R., Jorge B., Nadia M., and Lucy M. (2012). ECG portátil Portable ECG. Revista Colombiana de Física. 44(3):3–6.

Rashid M. (2002). Circuitos microelectrónicos: análisis y diseño. Primera. Thomson-Paraninfo.

Sedlácek J. and Szabó V. (2009). A simple economical building FDNR blocks with modern operational amplifiers. In Proceedings of the Progress in Electromagnetics Research Symposium-PIERS.1113-1117.

Sedra A. S. (2009). Circuitos Microelectrónicos. 5ta Edición. México, D.F.: Mc Graw Hill.

Senani V. (1979). Some observations concerning the methods of filter/oscillator realization using the concept of FDNR. Proc. IEEE. 67(12):1665–1666.

Silva, C. P., and Young, A. M. (2000). Introduction to chaos-based communications and signal processing. In Aerospace Conference Proceedings, IEEE. 1: 279-299.

Stavrinides, S. G., Anagnostopoulos, A. N., Miliou, A. N., Valaristos, A., Magafas, l., Kosmatopoulos, K., and Papaioannou, S. (2009). Digital chaotic synchronized communication system. J. Eng. Sci. Technol. Rev. 2(1):82–86.

Susan, D., and Jayalalitha, S. (2012). Frequency Dependent Negative Resistance-A Review. Res. J. Appl. Sci. Eng. Technol. 4(17):2988-2994.

Susan, D., and Jayalalitha, S. (2010). Analog filters using simulated inductor. ICMET 2010 - 2010 Int. Conf. Mech. Electr. Technol. Proc. Icmet. 659–662.

Szabó Z., Friedl M., and Sedláček J. (2013). Comparison of the Dynamic Range of FDNR Building Blocks. PIERS TAIPEI. 159–162.

Universidad Antonio Nariño (2015). Plan de estudios asignatura Sistemas Analógicos III. Recuperado el 10 de abril de 2016, de, http://www.uan.edu.co/ingenieria-electronica-plan-de-estudios.

Universidad del Norte. (2015). Plan de asignatura Electrónica II. Recuperado el 10 de abril de 2016, de, https://pomelo.uninorte.edu.co/pls/prod/bwckctlg.p_disp_course_detail?cat_term_in=201510andsubj_code_in=IENandcrse_numb_in=4030.

Universidad de la Costa. (2015). Plan de Estudios Académicos Ingeniería Electrónica. Recuperado el 10 de abril de 2016, de, http://www.cuc.edu.co/index.php?option=com_wrapperandview=wrapperandItemid=1957.

Yang X. and Shiyan Z. (1991). Design of FDNR continuous time MOSFET-C band-pass filters with low sensitivity and fewer number of op-amps. In IEEE International Sympoisum on Circuits and Systems. 3:1335-133

Zamora-Musa, R., Velez, J., Paez-Logreira, H., Coba, J., Cano-Cano, C., Palmera, O.M. Implementation of an open educational resource through the model of universal design for learning taking into account competency-based assessment and the individual needs of students (2017) Espacios, 38 (5), p. 3.

1. Investigador Asociado. Departamento de Ciencias de la Computación y Electrónica de la Universidad de la Costa– CUC, Colombia. Email: jsimanca3@cuc.edu.co

2. Investigador Senior. Sección de Ingeniería de Telecomunicaciones de la Pontificia Universidad Católica del Perú. Email: csilva@pucp.edu.pe

3. Investigador Asociado. Departamento de Ciencias de la Computación y Electrónica de la Universidad de la Costa– CUC, Colombia. Email: eramirez1@cuc.edu.co

4. Investigador Asociado. Departamento de Ingeniería de la Universidad del Norte, Colombia. Email: rubendams@gmail.com

5. Investigador Senior. Departamento de Ciencias de la Computación y Electrónica de la Universidad de la Costa– CUC, Colombia. Email: acama1@cuc.edu.co